Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

11.2. Системы репликаций 481

Читатель сможет легко найти языки, не удовлетворяющие

этим необходимым условиям.

Из примера 11. 1 (каждое семейство SREP (g) содержит бес-

конечные языки) и леммы 11.11 (существуют конечные языки,

не лежащие в SREP (g) при любом g ∈ D) мы получаем сле-

дующий результат.

Теорема 11.3. Семейство FIN несравнимо с любым из се-

мейств SREP (g), g ∈ D.

Благодаря примеру 11.1 мы, кроме того, знаем, что все се-

мейства SREP (g), g ∈ {Mp, Ml, aM, t}, содержат не контекст-

но-свободные языки. На самом деле верен более сильный ре-

зультат.

Теорема 11.4. Любое из семейств SREP (g), g ∈ {Mp, M l,

aM, t}, несравнимо с каждым подсемейством MAT

, содер-

жащим по крайнем мере один неодноэлементный конечный

язык.

Доказательство. Для системы γ = ({a}, aa, a#a) получаем

(γ) = {a

| n > 1}

при каждом g ∈ {Mp, Ml, aM, t}. Согласно [129], этот язык не

лежит в семействе MAT

С другой стороны, в SREP (g) нет неодноэлементных ко-

нечных языков при любом g ∈ D.

Некоторые другие репликационные семейства содержат

только регулярные языки.

Теорема 11.5. SREP (g) ⊆ REG, g ∈ {am, mp}.

Доказательство. Возьмем репликационную систему γ =

(V, w, a#b). Предположим, что w = a

. . . a

при a

∈ V ,

1 6 i 6 n, n > 1. Рассмотрим строку

= s

. . . s

n−1

где s

, s

, . . . , s

— новые символы.

Выделим в w все позиции подстроки ab. Пусть 1 6 i

< i

· · · < i

< n — номера этих позиций:

482 11. И вновь о сплетении

= a, a

= b, 1 6 q 6 r.

Выписанные номера указывают все места вставок.

Теперь парами (j

, k

), . . . , (j

, k

) обозначим все минималь-

ные подстроки w вида z

= bz

= z

a. Другими словами,

= a

. . . a

, 1 6 l 6 t.

Для каждой такой строки z

и каждой определенной выше

позиции для вставки i

рассмотрим строку

l,q

= s

(l,q)

−1

(l,q)

. . . s

(l,q)

−1

(l,q)

где s

(l,q)

— новые символы, ассоциированные с h, z

и i

Обозначим через K множество всех символов s

, 0 6 i 6 n,

и s

(l,q)

, 1 6 l 6 t, j

− 1 6 h 6 k

, 1 6 q 6 r. Построим конечный

недетерминированный автомат (c λ-переходами)

M = (K, V, s

, {s

}, δ),

где δ определено, как предложено на рис. 11.1. Таким образом,

оно учитывает все связи в w

, в строках z

, а также связи,

возникающие в резул ьтате вставок строк z

в w

в соответству-

ющие позиции:

= δ(s

i−1

, a

) при 1 6 i 6 n,

(l,q)

∈ δ(s

(l,q)

h−1

, a

) при j

6 h 6 k

, 1 6 l 6 t, 1 6 q 6 r,

(l,q)

−1

∈ δ(s

, λ), s

∈ δ(s

(l,q)

, λ) при 1 6 l 6 t, 1 6 q 6 r.

Докажем, что L

(γ) = L(M).

Включение L(M) ⊆ L

(γ) очевидно: мы начинаем с w ∈

(γ) и вставляем в прави льн ые позиции правильные под-

строки.

Обратно, рассмотрим строку x ∈ L

(γ). Если x = w, то

x ∈ L(M). Если w

x, то w = w

abw

, x = w

aybw

при некоторой минимальной y ∈ Sub(w), y = by

= y

a. Из

определения δ имеем x ∈ L(M). Будучи минимальной, y не со-

держит подстроку ab, и значит, места вставок в x — это ли бо

места вставок из w

, w

, либо два новых, полученных благо-

даря внедрению y, поскольку ayb = aby

b = ay

ab. Каждое из

11.2. Системы репликаций 483





-B

t,q

. . .

2,q



 





1,q

Рис. 11.1. Действие конечного автомата M из доказательства

теоремы 11.5.

этих двух подслов ab из ayb включает один символ, уже су-

ществующий в w. Если строка z = bz

= z

a подходит для

вставки в x в одном из этих мест, то это возможно также и в

автомате A (см. рис. 11.1). Индукцией по длине репликацион-

ной цепочки мы устанавливаем, что в каждой строке x, такой,

что w

∗

x, места вставки соответствуют местам вставки из

w. Следовательно, если x ∈ L(M) и x

, то x

∈ L(M).

Таким образом, L

(γ) ⊆ L(M).

Эти рассуждения проходят также и при g = mp: в этом

случае мы имеем t = 1 (для вставки подходит только одна

строка), в остальном же аргументация остается прежней.

Заметим, что в конструкции автомата M можно использо-

вать «минимальные циклы» из-за минималь ности вставок. Од-

нако, как мы увидим в следующей теореме, некая модификация

этой конструкции сможет функционировать и при свободном

режиме.

Теорема 11.6. SREP (g) ⊆ REG, g ∈ {ml, af}.

Доказательство. Мы воспользуемся той же конструкцией, что

и в доказательстве предыдущей теоремы, внеся следующие из-

менения.

В случае g = ml мы должны рассмотреть в w (единствен-

ную) минимальную самую левую подстроку z вида z = bz

a вместо строк z

, . . . , z

, рассматривавшихся ранее. Так как

репликационный режим — минимальный самый левый, только

эта строка может вставляться в произвольное слово из L

(γ).

484 11. И вновь о сплетении

(Заметим, что z может не быть минимальной в am смысле. Рас-

смотрим, например, w = cbcbab при контексте вставки (a, b). В

режиме выбора самой левой минимальной строки мы должны

взять z = bcba, в то время как для am режима, эта строка не бу-

дет минимальной, поскольку содержит подстроку ba. Именно

по этой причине предложенное ранее доказательство не рас-

пространяется автоматически на случай g =ml.)

При g = af считаем, что z

, z

, . . . , z

из доказательства

предыдущей теоремы суть все подстроки w вида z

= bz

= z

не содержащие подстроку ab. В то же время z

может содер-

жать b, а z

— a. (И строки z

, z

, и t могут быть другими,

чем в предыдущей теореме.) Пусть y — подстрока w, которая

может быть вставлена на некотором этапе вывода. Тогда мы

можем записать y = z

. . . z

, где z

— вышеуказанные

строки. Доп устим, мы хотим вставить строку y в позицию i

Из определения δ видно, что из s

можно дойти до состояния

перед каждым z

, 1 6 j 6 m, и вернуться к s

. Значит, су-

ществует путь через состояния M, охватывающие строку z

. . . z

= y. Включение L

(γ) ⊆ L(M) верно и в этом слу-

чае.

Контраст с предыдущими теоремами составляет

Теорема 11.7. Семейства SREP (ap ) и SREP (al) содержат

не к онтекстно-свободные языки.

Доказательство. Рассмотрим репликационную систему

γ = ({a, b, c, d}, bcabda, a#b).

В обоих режимах ap и al все порождаемые строки начинают-

ся с символа b, следовательно, два этих режима совпадают,

(γ) = L

(γ).

Рассмотрим регулярный язык

R = (bca)

(bda)

Обозначим V = {a, b, c, d} (с д анн ым упорядочением симво-

лов). Если L

(γ) — контекстно-свободный язык, то язык

L = L

(γ) ∩ R

11.2. Системы репликаций 485

— тоже контекстно-свободный, следовательно, Ψ

(L) — полу-

линейное множество. Возьмем полулинейное множество

T = {(n, m, p, p) | n, m, p > 1}.

Семейство полулинейных множеств векторов замкнуто отно-

сительно пересечения. Поэтому, из L

(γ) ∈ CF следует, что

(L) ∩ T — полулинейное множество.

Мы, однако, утверждаем, что

(L) ∩ T = {(2

n+1

, 2

n+1

, 2

) | n > 1}. (∗)

Последнее же множество, безусловно, полулинейным не явля-

ется.

Докажем равенство (∗). Пусть мы породили строку x =

(bca)

(bda)

(первоначально i = 1), и теперь x используем в

качестве строки-вставки между a и b в середине x. Тогда y =

(bca)

(bda)

. Можно повторять этот процесс, и значит, каждая

строка вида z = (bca)

(bda)

, j > 0, лежит в L

(γ). Такие

строки лежат в R, и, следовательно, в L. Поскольку Ψ

(z) =

j+1

, 2

j+1

, 2

), мы имеем включение ⊇.

Обратно, исследуем строки y ∈ L при каждом Ψ

(y) ∈ T .

Будучи элементом L, y имеет вид y = (bca)

(bda)

, i, j > 1.

Должно выполняться равенство i = j, так как Ψ

(y) ∈ T .

Поэтому мы должны рассматривать строки из L

(γ) вида y =

(bca)

(bda)

, i > 1.

Поскольку мы работаем в ap режиме, мы обязаны при ре-

пликации строки (bca)

(bda)

, k > 1, выбрать строку вида

= (bca)

, r 6 k, или вида z

= (bca)

(bda)

, s 6 k. Поэтому

в каждый момент мы получаем строку y

с |y

> |y

. Если

> |y

, то ни для одной строки y

с условием y

∗

равенство |y

= |y

выполняться не будет.

Из строки y

, не лежащей в (bca)

(bda)

, и значит, имеющей

вид u

, вывести строку y

∗

), принадлежащую

(bca)

(bda)

, невозможно.

Итак, для производства строк ви да y = (bca)

(bda)

, мы

должны использовать только строки этого же вида и на каж-

дом репликационном шаге в качестве вставки брать текущую

486 11. И вновь о сплетении

строку целиком. Отсюда следует, что каждая репликация дуб-

лирует целую строку, а значит, для степени i выполняется ра-

венство i = 2

, n > 0. Это доказывает включение ⊆ в отноше-

нии (∗).

Следствие 11.2. Семейства SREP (ap) и SREP (al) не срав-

нимы с любым из подсемейств CF, содержащим по крайней

мере один неодноэлементный конечный язык.

Поскольку MAT содержит не полулинейные языки, преды-

дущая теорема, в проти вопо ложность теореме 11.4, не дает

оснований утверждать, что в SREP (ap) и SREP (al) есть язы-

ки, не лежащие в семействе MAT или M AT

Различие между режимами ap, al и af, am, ml, mp оказыва-

ется достаточно неожиданным (af и am ведут себя одинаково,

а ap и mp, или al и ml — не похоже).

Из лемм 11.14 и 11.15 мы находим, что для системы γ

примере 11.1 языки L

(γ

) при g ∈ {ap, mp, al, ml, af, am} не

лежат в SREP (g

) при g

∈ {Mp, Ml, aM, t}, следовательно,

верна

Лемма 11.17. SREP (g) − SREP (g

) 6= ∅ при всех g ∈ {ap,

mp, al, ml, af, am}, g

∈ {Mp, Ml, aM, t}.

Из леммы 11.16 мы находим, что L

(γ

) /∈ SREP (g

) при

g ∈ {Mp, Ml, aM, t}, g

∈ {af, am, al, ml, ap, mp}, следователь-

но, верна

Лемма 11.18. SREP (g) − SREP (g

) 6= ∅ при всех g ∈ {Mp,

Ml, aM, t}, g

∈ {af, am, al, ml, ap, mp}.

Из примера 11.2 и леммы 11.12 мы получаем след ующий

результат.

Лемма 11.19. SREP (g) − SREP (g

) 6= ∅ при всех g ∈ {al, ml,

af, am, aM, Ml}, g

∈ {ap, mp, Mp, t}.

Лемма 11.20. SREP (Ml) = SREP (aM).

Доказательство. Возьмем γ = (V, w, a#b) и рассмотрим ре-

пликационный шаг z

. Имеем z = z

abz

и z

= z

axbz

при x ∈ Sub(z), z = x

, x = bx

= x

a, и x — максимальная

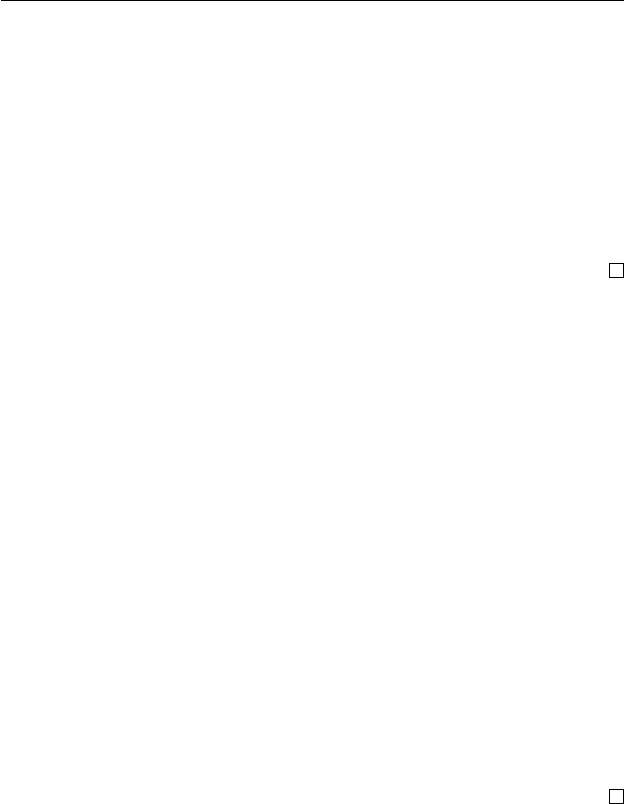
11.2. Системы репликаций 487

подстрока в z, т. е. никакая надстрока y строки x не может быть

представлена в виде y = by

= y

a. Если x не является самой

левой в z, то z = x

и |x

| < |x

|. Тогда x не максимальна:

z = x

для y = by

= y

a, |y| > |x|, и значит, x ∈ Sub(y),

противоречие. Поэтому и z

, т. е. L

(γ) ⊆ L

(γ).

Обратно, легко видеть, что z

влечет z

и, след овател ьно , L

(γ) ⊆ L

(γ). Таким образом, L

(γ) =

(γ), и значит, SREP (aM) ⊆ SREP (M l).

Обратное включение может быть получено тем же путем.

Лемма 11.21. SREP (t) ⊂ SREP (g), g ∈ {M l, M p, aM}.

Доказательство. Возьмем репликационную систему γ =

(V, w, a#b). Есл и L

(γ) = {w}, то L

(γ) = L

(γ

) для γ

(V ∪ {c}, w, c#c), и c /∈ V , пр и всех g из условия.

Если L

(γ) 6= {w}, то w = bw

a, и все z, такие, что w

∗

имеют вид z = bz

a при всех g. Следовательно, в каждый

момент репликационной цепочки получаемая строка является

одновременно максимальным префиксом, максимальной са-

мой левой, и произвольной максимальной вида bya. Поэтому

(γ) = L

(γ) для всех g ∈ {Ml, Mp, aM}. Мы получаем

SREP (t) ⊆ SREP (g) для g из условия леммы.

Из леммы 11.17 мы знаем, что для g ∈ {aM, Ml} эти вклю-

чения собственные. Для g = Mp рассмотрим систему

γ = ({a, b}, aab, a#a).

Получаем

(γ) = {a

b | n > 1}.

Согласно леммам 11.13 и 11.14, этот язык не принадлежит се-

мейству SREP (t).

Лемма 11.22. SREP (g) − SREP (g

) 6= ∅, g ∈ {am, ml, mp},

∈ {aM, t, Mp, ap, al, Ml, af}.

Доказательство. Рассмотрим репликационную систему

γ = ({a, b}, aabaa, a#a).

488 11. И вновь о сплетении

Для g из условия ст рока-вставка всегда совпадает с a, следо-

вательно,

(γ) = a

aba

Предположим, для системы γ

= (V, aabaa, c#d) выполняет-

ся L

(γ) = L

(γ

) при каком-нибудь из указанных g

. (Самая

короткая строка в языке — это всегда порождающая его ак-

сиома репликационной системы.) Ясно, что c, d ∈ {a, b}. Если

один из c, d равен b, то при каждом z

вводится один

новый символ b, что приводит к появлению «паразитических»

строк. Поэтому (c, d) = (a, a). При всех режимах g

мы можем

взять для вставки текущую строку целиком (а при g

∈ {aM,

t, Mp, Ml} это обязательно). В результате снова удваивается

число вхождений символа b. Равенство L

(γ) = L

(γ

) невоз-

можно.

Лемма 11.23. SREP (g) − SREP (g

) 6= ∅ для всех g ∈ {af, ap,

al}, g

∈ {am, mp, ml}.

Доказательство. Рассмотрим снова систему

γ = ({a, b}, aabaa, a#a).

При всех указанных режимах g мы можем провести реплика-

цию

aabaa

a(aabaa)abaa = z

(мы вставляем целую строку между п ервыми двумя вхожде-

ниями a).

Предположим, что L

(γ) = L

(γ

) при некотором γ

(V, aabaa, c#d). Если (c, d) = (a, a), то мы должны вставлять

a (это мин имальн ая подстрока вида x = ax

= x

a), следо-

вательно, число вхождений b не увеличивается, и указанную

строку z получит ь невозможно. Если (c, d) = (a, b), то строка

для вставки — ba, и значит, мы получаем

(γ

) = a(ab)

aa.

Если (c, d) = (b, a), то вставляемая строка равна ab, и мы по-

лучаем

(γ

) = aa(ba)

11.2. Системы репликаций 489

Ни в одном из возникающих случаев указанную строку z мы не

получим, а значит, равенство L

(γ) = L

(γ

) невозможно.

Лемма 11.24. SREP (Mp) ⊂ SREP (Ml).

Доказательство. Если γ = (V, w, a#b) — репликационная си-

стема и L

(γ) = {w}, то, очевидно, L

(γ) ∈ SR EP (Ml).

Если L

(γ) бесконечен, то w имеет вид w = zw

, z = bz

a, и все строки в L

(γ) начинаются с символа b. Следова-

тельно, самая левая подстрока, выбираемая для вставки, есть

всегда префикс текущей строки, и значит, L

(γ) = L

(γ),

т. е. SREP (Mp) ⊆ SREP (M l ).

Это включение собственное, так как язык L = {ba

| n >

1} не лежит в семействе SREP (M p) (лемма 11.12), но L =

(γ) при γ = ({a, b}, baa, a#a).

Лемма 11.25. SREP (mp) ⊂ SREP (ml), SREP (ap) ⊂

SREP (al).

Доказательство. Включения получаются так же, как и

в предыдущем доказательстве: если γ = (V, w, a#b), то

(γ) = L

(γ) и L

(γ) = L

(γ).

Строгость следует из леммы 11.19.

Лемма 11.26. SREP (g) − SREP (am) 6= ∅, g ∈ {mp, ml}.

Доказательство. Рассмотрим систему

γ = ({a, b, c}, bcabacbca, a#b).

И при g = mp, и при g = ml строка-вставка всегда должна

равняться bca. Вид аксиомы γ, bcabacbca, не оставляет выбора:

bcabacbca

(bca)

bacbca.

Следовательно, в результате n вставок мы порождаем строку

(bca)

bacbca. Поэтому для каждой строки x из L

(γ) выполня-

ется |x|

= |x|

Предположим теперь, что L

(γ) = L

(γ

) при некоторой

= (V, w, d#e). Тогда bcabacbca, будучи самой короткой стро-

кой L

(γ), является аксиомой и для γ

, т. е. w = bcabacbca.

Предположим, что d 6= e. Очевидно, они лежат в {a, b, c}.

Для любой такой па ры d, e в w есть подстрока ed, которую в

490 11. И вновь о сплетении

силу ее минимальности можно взять в качестве вставки. Для

получаемой в результате такой репликации строки w

выпол-

няется |w

= |w

+ 1 при {a, b, c} = {d, e, f}. Сле-

довательно, w

не лежит в L

(γ), противоречие. Если d = e,

то строка для вставки есть d = e. Она только увеличивает

число вхождений d = e, снова приводя к паразитическим стро-

кам.

Лемма 11.27. SREP (g) − SREP (af) 6= ∅, g ∈ {ap, al}.

Доказательство. Возьмем снова систему

γ = ({a, b, c}, bcabacbca, a#b)

из предыдущего д оказательства. И при g =ap, и при g =al

строка-вставка начинается с bca, префикса аксиомы. Более то-

го, префикс bca сохраняется при любой репликации, поэтому

он обязан входить в любую строку-вставку. Следовательно, ни

при каких d, e ∈ {a, b, c} и константе k нельзя указать последо-

вательность строк из L

(γ) w

, w

, . . . , для которой |w

строго

возрастает с ростом i, в то время как |w

6 k.

Предположим тепер ь, что L

(γ) = L

(γ

) для некоторо-

го γ

= (V, w, d#e). Ясно, что w = bcabacbca. Независимо от

того, чему равны символы d, e, подстрока ed появляется в w

(а также во всех строках, получаемых при помощи реплика-

ции). Поэтому L

(γ

) содержит строки со сколь угодно боль-

шим числом вхождений d, e и ограниченным числом вхождений

f = {a, b, c} − {d, e}. Такие строки не лежат в L

(γ), противо-

речие.

Лемма 11.28. SREP (af) − SREP (al) 6= ∅, SREP (am) −

SREP (ml) 6= ∅.

Доказательство. Рассмотрим систему γ = ({a, b, c}, w, a#b) с

w = bcacbab. В обоих режимах выбора строки-вставки af и

am мы можем выбрать в w подстроку ba, следовательно, мы

можем получить строки, содержащие сколь угодно много a и

b, но ограниченное число символов c. Для того чтобы порож-

дать такие строк и при помощи системы γ

= (V, w, d#e) в од-

ном из режимов al, ml, мы должны иметь {d, e} = {a, b}. Если