Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.


10.2. Взаимодействующие распр еде лен ные H-системы 431
∪ {X
2i
D
i
Z | 1 6 i 6 n}
∪ {X
2i
Z | 0 6 i 6 n − 1}
∪ {ZY
2i
| 0 6 i 6 n},
R
1
= {#uY $Z#vY | u → v ∈ P }
∪ {#D
i
Y $Z#Y
2i
, X#$X
2i
D
i
#Z | 1 6 i 6 n}
∪ {#Y
2i+1
$Z#Y
2i
, X
2i+1
#$X
2i
#Z | 0 6 i 6 n − 1},
V
1
= N ∪ T ∪ {B, X, Y } ∪ {X
2i+1
, Y
2i+1
| 0 6 i 6 n − 1},
A
2
= {ZY
2i−1
, X
2i−1
Z | 1 6 i 6 n} ∪ {ZZ},
R
2
= {#Y
2i
$Z#Y
2i−1
, X
2i
#$X
2i−1
#Z | 1 6 i 6 n}
∪ {X
0
B#$#ZZ, #Y
0
$ZZ# },
V
2
= N ∪ T ∪ {B, X
0
, Y
0
} ∪ {X
2i
, Y
2i
| 1 6 i 6 n},
A
3
= {ZY, XZ, ZY
0
, ZX
0
},
R
3
= {#Y
0
$Z#Y, X
0
#$X#Z, #Y
0
$Z#Y
0
, X
0
#$X
0
#Z},
V
3
= N ∪ T ∪ {B, X
0
, Y
0
}.
Исследуем работу Γ. В ее основе — уже знакомая нам идея
имитации и переброски. Начав со строки вида XwY (такой вид
имеет а ксиома XBSY ), первая компонента может либо смоде-
лировать в суффиксе w правило из P , использовав для этого
правила #uY $Z#vY , u → v ∈ P , либо начать ротацию стро-
ки. В первом случае возникающая строка вновь ограничена
маркерами X , Y , и значит, процесс может быть повторен. При
удалении символа D
i
с правого конца w (w = w
1
D
i
, 1 6 i 6 n)
символ Y заменяется на Y
2i
:
(Xw
1
|D
i
Y, Z|Y
2i
) |= (Xw
1
Y
2i
, ZD
i
Y ).
(Заметим, что B может быть удален наряду с любым символом
из N ∪ T .)
Строки, содержащие Z, не могут быть переброшены из од-
ной компоненты в другую. А из двух таких строк получить пу-
тем сплетения новую, а тем более терминальную, строку невоз-
можно. Рассмотрим, например, строку ZD
i
Y . Снова применяя

432 10. Распределенные H-системы
правило #D
i
Y $Z#Y
2i
, мы пол учаем строки ZY
2i
, ZD
i
Y . Ана-
логичный результат будет верен и во всех остальных случаях.
Строку Xw
1
Y
2i
передать нельзя, но в первой компоненте
возможно следующее сплетение:
(X|w
1
Y
2i
, X
2j
D
j
|Z) |= (XZ, X
2j
D
j
w
1
Y
2i
)
для некоторого 1 6 j 6 n. Две эти операции можно вып олн ить
и в обратном порядке, результат останется прежним.
Строки, огран ичен ные маркерами X
r
, Y
s
с четными r, s,
нельзя ввести в новые сплетения, зато можно передать во
вторую компоненту. Здесь осуществимы два сплетения, умень-
шающие на единицу каждый из индексов у X и Y . При
выполнении только одного сплетения, передача невозможна.
Таким образом, получаем:
(X
2j
|D
j
w
1
Y
2i
, X
2j−1
|Z) |= (X
2j
Z, X
2j−1
D
j
w
1
Y
2i
),
(X
2j−1
D
j
w
1
|Y
2i
, Z|Y
2i−1
) |= (X
2j−1
D
j
w
1
Y
2i−1
, ZY
2i
).
Снова порядок этих двух операций не важен.
Строка с нечетными индексами концевых маркеров может
быть возвращена в первую компоненту. Эти действия могут и
должны быть повторены, иного способа избавиться от нетер-
минальных символов не существует. Строка с нулевым индек-
сом концевого маркера перейти во вторую компоненту не мо-
жет. Поэтому если индекс только одного из концевых маркеров
X , Y равен 0, то строка будет «потеряна»: ее нельзя ни переда-
вать, ни вводить в новые сплетения. Если оба маркера имеют
индекс 0, то строку можно передать третьей компоненте.
В третьей компоненте строка вида X
0
wY
0
может быть пре-
вращена в одну из строк: XwY (эта строка переносится в пер-
вую компоненту, что позволяет повторять процесс имитации
правил из P или ротации строки), в строку X
0
wY
0
или же в
строку со смешанным типом маркеров X, Y — со штрихом и
без штриха. В последнем случае, она снова оказывается «поте-
рянной».

10.2. Взаимодействующие распр еде лен ные H-системы 433
Строка вида X
0
wY
0
может быть передана только во вторую
компоненту, где возможны л ишь два сплетен ия:
(X
0
B|w
1
Y
0
, |ZZ) |= (X
0
BZZ, w
1
Y
0
),
(w
1
|Y
0
, ZZ|) |= (w
1
, ZZY
0
),
при условии, что w = Bw
1
(которое гарантирует, что эта строка
имеет ту же перестановку, что и соответствующая строка, про-
изводимая G). Строка без концевых маркеров не может всту-
пать в новые сплетения. Если она терминальная, то ее можно
передать первой компоненте, а значит, это элемент L(Γ). В про-
тивном случае она «потеряна».
Итак, индексы двух маркеров X, Y должны достигнуть ну-
левых значений одновременно. Это возможно, если только они
изначально были одинаковыми. Как и в рассмотренном ранее
случае, мы должны иметь i = j. Это означает, что символ
D
i
, стертый с правого конца w, нужно одновременно ввести с
левого конца w. Таким образом, этап переброски выполняет-
ся корректно, а значит, могут быть получены все циклические
перестановки данной строки. Следовател ьно, все выводы в G
можно имитировать в Γ, и обратно, только строки из L(G) мо-
гут быть в качестве терминальных посланы в первую компо-
ненту Γ. Таким образом, L(G) = L(Γ).
Взаимодействующие распределенные H-системы степени 1
не используют передачу, и значит, являются расширенными ко-
нечными H-системами. Ввиду результатов главы 7, мы можем
записать
CDH
1
= R EG ⊂ CDH
2
(то, что второе включение собственное, доказано примером пе-
ред теоремой 10.4).
Вопрос, можно ли включен ие CDH
2
⊆ CDH
3
заменить
равенством, и, следовательно, может ли быть усилена до
n = 2 теорема 10.4, до сих пор открыт. Мы ожидаем, что
ответ будет отрицательным, более того, мы предполагаем, что
CDH
2
⊂ CF . Этот вопрос более интересен с математической
точки зрения, и гораздо менее — для ДНК-вычислений: по-
водом к рассмотрению распределенных H-систем послужило

434 10. Распределенные H-системы
желание уменьшить число правил сплетения в каждой ком-
поненте. Интуитивно понятно, что малое число компонент
должно компенсироваться их большими размерами, а это
противоречит нашей цели.
Рассмотрим теперь саму проблему, которая послужила при-
чиной введения распределенных H-систем — ограничение чис-
ла правил, работающих вместе. Для взаимодействующей рас-
пределенной H-системы Γ = (V, T, (A
1
, R
1
, V
1
), . . . , (A
n
, R
n
, V
n
))
мы обозначим через deg(Γ) степень Γ (число компонент n), че-
рез rad(Γ) — максимум радиусов правил в Γ, и
size(Γ) = max{card(R
i
) | 1 6 i 6 n}.
Видоизменив конструкцию из доказательства теоремы 10.4,
мы сможем охаракт еризов ать семейство RE с помощью взаи-
модействующих распределенных H-систем минимального раз-
мера, равного единице (конечно, это получается за счет снятия
ограничений на число компонент).
Теорема 10.5. Для каждой грамматики G = (N, T, S, P ) ти-
па 0 существует взаимодействующая распределенная H-си-
стема Γ, такая, что L(G) = L(Γ), и
deg(Γ) = 2(card(N ∪ T ) + 1) + card(P ) + 9,
size(Γ) = 1,
rad(Γ) = card(N ∪ T ) + 2.
Доказательство. Для грамматики G = (N, T, S, P ) типа 0 рас-
смотрим новый символ B, и обозначим для удобства N ∪ T ∪
{B} = {D
1
, D
2
, . . . , D
n
}. Поскольку N 6= ∅, T 6= ∅, имеем
n > 3. Предположим, что правила из P пронумерованы r
1
,
. . . , r
m
, где m = card(P ). Мы построим взаимодействующую
распределенную H-систему Γ с алфавитом
V = N ∪ T ∪ {X, X
0
, X
00
, Y, Y
0
, Y
00
, Z, B, C, E},
терминальным алфавитом T , и с компонентами, описанными
ниже. Мы пронумеруем эти компоненты элементами α из мно-
жества
M = {1, 2, 3, 4, 5, 6, 7, 8, 9}

10.2. Взаимодействующие распр еде лен ные H-системы 435
∪ {D
i
, D
0
i
| 1 6 i 6 n} ∪ {r
i
| 1 6 i 6 m},
а именно
α = r
i
: A
α
= {XBSY, Zv
i
Y },
R
α
= {#u
i
Y $# v
i
Y }, для r
i
: u
i
→ v
i
∈ P,
V
α
= N ∪ T ∪ {X, Y, B}, где i = 1, 2, . . . , m;
α = D
i
: A
α
= {ZC
i
Y },
R
α
= {#D
i
Y $Z#C
i
Y
0
},
V
α
= N ∪ T ∪ {X, Y, B}, где i = 1, 2, . . . , n;
α = 1 : A
α
= {ZY
00
},
R
α
= {#CY
0
$Z#Y
00
},
V
α
= N ∪ T ∪ {X, Y
0
, B, C};
α = 2 : A
α
= {X
0
CZ},
R
α
= {X#$X
0
C#Z},
V
α
= N ∪ T ∪ {X, Y
00
, B, C};
α = 3 : A
α
= {ZY
0
},
R
α
= {#Y
00
$Z#Y
0
},
V
α
= N ∪ T ∪ {X
0
, Y
00
, B, C};
α = 4 : A
α
= {XZ},
R
α
= {X
0
#$X#Z},
V
α
= N ∪ T ∪ {X
0
, Y
0
, B, C};
α = D
0
i
: A
α
= {X
00
D
i
Z},
R
α
= {XC
i
#$X
00
D
i
#Z},
V
α
= N ∪ T ∪ {X, Y
0
, B, C}, где i = 1, 2, . . . , n;
α = 5 : A
α
= {ZY },
R
α
= {#Y
0
$Z#Y },
V
α
= N ∪ T ∪ {X
00
, Y
0
, B};
α = 6 : A
α
= {XZ},
R
α
= {X#Z$X
00
#},
V
α
= N ∪ T ∪ {X
00
, Y, B};

436 10. Распределенные H-системы
α = 7 : A
α
= {ZE},
R
α
= {#Y $Z#E},
V
α
= T ∪ {X, Y, B};
α = 8 : A
α
= {ZZ},
R
α
= {#ZZ$XB#},
V
α
= T ∪ {X, E, B};
α = 9 : A
α
= {ZZ},
R
α
= {#E$ZZ#},
V
α
= T ∪ {E}.
Работа в Γ происходит следующим образом.
Ни одна терминальная строка не может вступить в спле-
тение, так как прав ила из R
α
, α ∈ M, содержат контрольные
символы X , X
0
, X
00
, Y, Y
0
, Y
00
, Z.
Компоненты, пронумерованные α = r
i
, 1 6 i 6 m, исполь-
зуются для имитации правил из P . Это делается на правом кон-
це текущей строки вида XwY , при w ∈ (N ∪ T ∪ {B})
∗
(только
такие строки допускаются фильтрами этих компонент):
(Xw
1
|u
i
Y, Z|v
i
Y ) |= (Xw
1
v
i
Y, Zu
i
Y ).
Строка Xw
1
v
i
Y имеет тот же тип (содержит подобные симво-
лы), что и входная строка Xw
1
u
i
Y . Побочный продукт, строка
Zu
i
Y , может войти в новое сплетение указанного типа, если
только u
i
= v
i
(следовательно, ничего нового произведено не
будет) или (с тем же эффектом) в сплетении типа
(Z|u
i
Y, Z|v
i
Y ) |= (Zv
i
Y, Zu
i
Y ).
Строку вида XwY , с w, состоящим только из символов из
N ∪ T ∪ {B}, можно передать в компоненту с номером α =
D
i
, 1 6 i 6 n. В ней символ D
i
, стоящий на правом конце w,
заменяется на C
i
:
(Xw
1
|D
i
Y, Z|C
i
Y
0
) |= (Xw
1
C
i
Y
0
, ZD
i
Y ).
Строка ZD
i
Y может вступить только в сплетение вида
(Z|D
i
Y, Z|C
i
Y
0
) |= (ZC
i
Y
0
, ZD
i
Y ),

10.2. Взаимодействующие распр еде лен ные H-системы 437
не произведя ничего нового. Первую строку можно передать
как компоненте с индексом α = 1, так и компоненте с α = D
0
j
,
1 6 j 6 n. Во втором случае никакое сплетение невозможно.
Компоненты, соответствующие α = 1, 2, 3, 4, перемещают
символ C с прав ого конца строки на левый:
(XC
s
wC
t
|CY
0
, Z|Y
00
) |= (XC
s
wC
t
Y
00
, ZCY
0
),
(X|C
s
wC
t
Y
00
, X
0
C|Z) |= (XZ, X
0
CC
s
wC
t
Y
00
),
(X
0
C
s+1
wC
t
|Y
00
, Z|Y
0
) |= (X
0
C
s+1
wC
t
Y
0
, ZY
00
),
(X
0
|C
s+1
wC
t
Y
0
, X|Z) |= (X
0
Z, XC
s+1
wC
t
Y
0
).
В результате один символ C переносится с правого конца стро-
ки XC
s
wC
t+1
Y
0
, s, t > 0, на левый. Эту операцию можно по-
вторять, поскольку возникающая строка снова содержит сим-
волы из N ∪T ∪{X, Y
0
, B, C}. «Основная строка», ограниченная
X , Y или же их штрихованными версиями, должна циркулиро-
вать по пути 1, 2, 3, 4 и обратно в 1. Строки же, получаемые
во время данных шагов и содержащие символ Z, могут участ-
вовать лишь в сплетениях, не производящих ничего нового.
В любой момент строка XC
s
wC
t
Y
0
, s, t > 0, произведенная
компонентой с α = 4, может быть передана в любую компонен-
ту с индексом α = D
0
i
, 1 6 i 6 n. Есл и i 6 s, мы получаем
(XC
i
|C
s−i
wC
t
Y
0
, X
00
D
i
|Z) |= (XC
i
Z, X
00
D
i
C
s−i
wC
t
Y
0
).
Если s > i или t > 1, строку X
00
D
i
C
s−i
wC
t
Y
0
нельзя пере-
дать ни в одну компоненту, поскольку фильтры не пропускают
строки, содержащие X
00
и C одновременно. Дальнейшее спле-
тение в компоненте с α = D
0
i
для строк, начинающихся с X
00
,
невозможно. Поэтому мы должны иметь s = i и t = 0. Это
означает, что, заменяя символ D
i
на C
i
, мы обязаны заново
ввести его с левого конца строки.
Таким образом, изменения строки сводятся к циклической
перестановке, которая делает возможным применение правил
из G в любом месте строки, порождаемой G (моделируемой
в Γ).
Теперь компоненты, пронумерованные α = 5, 6, заменяют
Y
0
на Y и X
00
на X, чтобы и имитацию правил из G, и ротацию

438 10. Распределенные H-системы
строки можно было повторить. Детали мы оставляем читате-
лю.
В любой момент любая строка, содержащая только симво-
лы из T ∪ {B}, может быть передана в компоненту с индексом
α = 7, которая введет символ E. Единственное продолжени е
теперь состоит в удален ии вспомогательных символов. Важно
отметить, что мы можем удалить B только вместе с X, а зна-
чит, лишь тогда, когда вводимая строка имеет ту же переста-
новку, что и в G. Операции, выполняемые последними тремя
компонентами нашей системы, таковы:
(XBx|Y, Z|E) |= (XBxE, ZY ),
(|ZZ, XB|xE) |= (xE, XBZZ),
(x|E, ZZ|) |= (x, ZZE).
Заметим, что при всех этих операциях мы имеем x ∈ T
∗
. Марш-
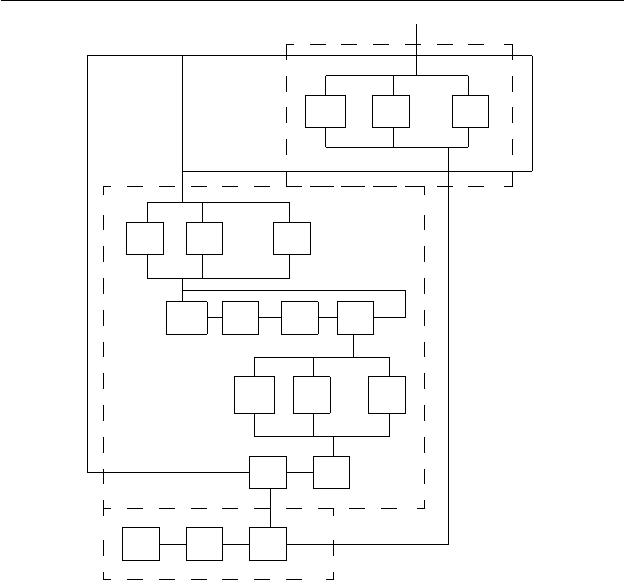
рут следован ия строки вида XwY , возможно, с штрихованны-
ми версиями X или Y , приведен на рис. 10.1. Блок A содержит
компоненты, выполняющие имитацию правил из P , блок B —
компоненты, выполняющие циклическую перестановку строки,
а блок C — компоненты, заканчивающие процесс.
Благодаря предшествующему обсуждению, нетрудно заме-
тить, что каждый вывод в G может быть имитирован в Γ, и
наоборот, все терминальные строки, достигающие первой ком-
поненты Γ, есть строки из L(G). Следовательно, L(G) = L(Γ).
Легко видеть, что Γ содержит m+2n+9 компонент (напом-
ним, что n = card(N ∪ T ∪ {B})), а rad(Γ) = n +1 (эта величина
достигается из-за R
α
при α = D
i
). Каждая компонента содер-
жит только одно правило сплетения, т. е. deg(Γ) = 1.
Замечание 10.2. Можно рассмотреть еще один параметр
акс(Γ) — наибольшее число аксиом в компонентах Γ. Тогда
для предыдущей конструкции акс(Γ) = 1.
Ценой увеличения количества компонент, мы также можем
ограничить и радиус получаемой системы.
10.2. Взаимодействующие распр еде лен ные H-системы 439
789
C
6 5
?
D
0
1
D
0
2
D
0
n
. . .
???
?
???
4321
- - -
?
D
1
D
2
D
n
. . .
???
?
???
B
r
1
r
2
r
m
. . .
???
???
A
?
-
?
?
?
?
?-
Рис. 10.1. Движение строк в Γ.
Теорема 10.6. Для каждой грамматики G = (N, T, S, P ) ти-
па 0 можно построить взаимодействующую распределенную
H-систему Γ, т акую , что:
1) L(G) = L(Γ),
2) deg(Γ) 6 3(card(N ∪ T ) + 1) + 2 · card(P ) + 4,
3) размер (Γ) = 1,
4) rad(Γ) = 2.
Доказательство. Изменим конструкцию системы Γ в д оказа-
тельстве теоремы 10.5 следующим образом.
Во-первых, удалим те компоненты в блоке B на рис. 10.1,
которые совершают в строке перестановку, и рассмотрим сле-
дующие компоненты для всех i = 1, 2, . . . , n:

440 10. Распределенные H-системы
α = D
i
: A
α
= {ZY
i
},
R
α
= {#D
i
Y $Z#Y
i
},
V
α
= N ∪ T ∪ {X, Y, B},
α = D
0
i
: A
α
= {X
0
D
i
Z},
R
α
= {X#$X
0
D
i
#Z},
V
α
= N ∪ T ∪ {X, Y
i
, B};
α = D
00
i
: A
α
= {ZY },
R
α
= {#Y
i
$Z#Y },
V
α
= N ∪ T ∪ {X
0
, Y
i
, B};
α = 1 : A
α
= {XZ},
R
α
= {X
0
#$X#Z},
V
α
= N ∪ T ∪ {X
0
, Y, B}.
Теперь переброска осуществляется следующим образом:
(Xw|D
i
Y, Z|Y
i
) |= (XwY
i
, ZD
i
Y ),
(X|wY
i
, X
0
D
i
|Z) |= (XZ, X
0
D
i
wY
i
),
(X
0
D
i
w|Y
i
, Z|Y ) |= (X
0
D
i
wY, ZY
i
),
(X
0
|D
i
wY, X|Z) |= (X
0
Z, XD
i
wY ).
Во-вторых, изменим имитирующие компоненты в блоке A
из рис. 10.1. Более точно, мы начнем с грамматики G в нор-
мальной форме Куроды (с правилами вида C → x, C ∈ N,
x ∈ (N ∪ T )
∗
, |x| 6 2, и CD → EF при C, D, E, F ∈ N ), пред-
положив при этом, что правила G пронумерованы.
Для каждого правила r : C → x мы введем в Γ компоненту
α = r : A
α
= {Zx},
R
α
= {#CY $Z#x},
V
α
= N ∪ T ∪ {X, Y, B},
а для каждого правила r : CD → EF — компоненты
α = r : A
α
= {ZY
r
},
R
α
= {C#DY $Z#Y
r
},
