Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

208 4 Carbon Problem

of the carbon eﬀect, because the eﬀect is not linear in C

YBCO

in some

cases. The parameter (4.45) should be estimated in experiment and depends

on the test temperature and crystallographic properties of HTSC. In particu-

lar, the absorption of carbon by a superconductor with free boundaries almost

invariably leads to expansion of crystalline lattice and corresponding change

of elastic properties.

Similar to the hydrogen eﬀect in intermetallic compounds [616], an ex-

istence of the carbon inﬂuence on elastic properties (in particular, shear

modulus) may be assumed due to an electronic eﬀect. The addition of car-

bon and the contribution of electrons at the Fermi level moves the Fermi

level and results in a corresponding change of temperature dependence of

the elastic properties. Carbon contributes electrons in the conduction band

and thereby changes the concentration of the conductivity electrons [1030]

that also changes electronic contribution to the elastic constants. The sign

and magnitude of the eﬀect depend on the electronic band structure and

the density of states at the Fermi level. In addition to these long-range ef-

fects of the carbon, there are other, more local eﬀects: (i) the direct carbon–

superconductor ion potential contributes to the elastic constants, and the

interstitial carbon may also aﬀect the superconductor ion–superconductor ion

potential [616]; (ii) direct inﬂuence on elastic constant of the optical phonons

due to the carbon vibrations [311]; and (iii) mechanical relaxation (Snoek ef-

fect) of the interstitial carbon in response to strain [655]. However, note that

for actual statement of the above carbon eﬀects on elastic properties of HTSC,

it is necessary to carry out intensive test investigations.

Then, in the present model simple mixture rules (4.43) and (4.44) have

been used for the derivation of the energy of de-cohesion and the maximum co-

hesive tractions. However, note that the maximum hydrostatic stress, which

is expected ahead of the crack tip in an elastic–plastic material before the

precipitation of near-tip carbonates, is recovered after their fracture. Conse-

quently, the strong eﬀect of hydrostatic stress distribution on carbon diﬀusion

and carbonate precipitation near the crack tip has been taken into account.

At the same time, if perfect cohesion is considered, carbon precipitates at the

tip, and no ductile ligament is formed during fracture similar to its occurrence

for hydrides in metals [1110]. Therefore, the de-cohesion model improves the

performance of the carbon embrittlement model, which is based on elastic be-

havior of the material. Moreover, the de-cohesion model takes into account the

time variation of the de-cohesion energy due to the time-dependent process

of carbonate precipitation.

Finally, note that a similar mathematical model and governing equations

may be obtained for other HTSC under carbon embrittlement. Finite-element

scheme for numerical realization of the governing equations is presented in

Appendix B.

4.4 Modeling of Carbon Segregation and Fracture Processes of HTSC 209

4.4 Modeling of Carbon Segregation

and Fracture Processes of HTSC

It could be proposed that carbon can segregate not only to grain bound-

aries, but also to crack surfaces and dislocations, where lattices are distorted.

Therefore, two microcracking processes are possible: continuously slow crack

growth and discretely rapid crack growth, associated with high amounts of

acoustic emissions. Then, the carbon segregation processes can be studied by

using the microscopic models of the equilibrium slow and fast crack propaga-

tion and also a steady-state crack growth, which are screened by dislocation

ﬁeld [812].

4.4.1 Equilibrium Slow and Fast Crack Growth

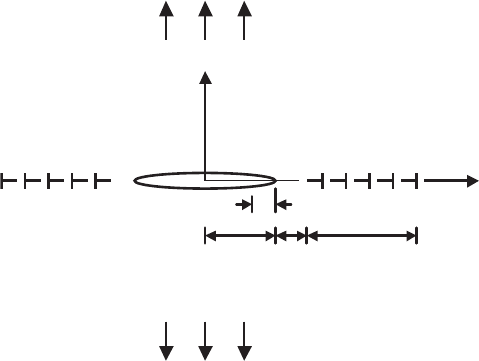
Consider an intergranular crack of length, 2a, in a carbonated HTSC (Fig.

4.13). The crack lies along x-axis in an elastic–plastic isotropic body with

shear modulus, G, Poisson ratio, ν, yield strength, σ

, and work hardening

factor, n. The body is loaded by a remote stress, σ

parallel to the y-axis at

a constant temperature, T .Atthex-axis, two linear dislocation arrays with

the length, r

, are located at the distance, d, from the crack tips. This model

proposes that an intergranular crack tip maintains an atomistic sharpness

and a local equilibrium condition in the presence of screening dislocations.

It is assumed that all geometrical parameters of the crack tip, presented in

Fig. 4.14 (in particular, the size of the arc-shaped crack tips, q,andacracktip

displacement, δ

), remain constant during plastic deformation. The condition

Fig. 4.13. Schematic representation of intergranular crack, screened by linear dis-

location array

210 4 Carbon Problem

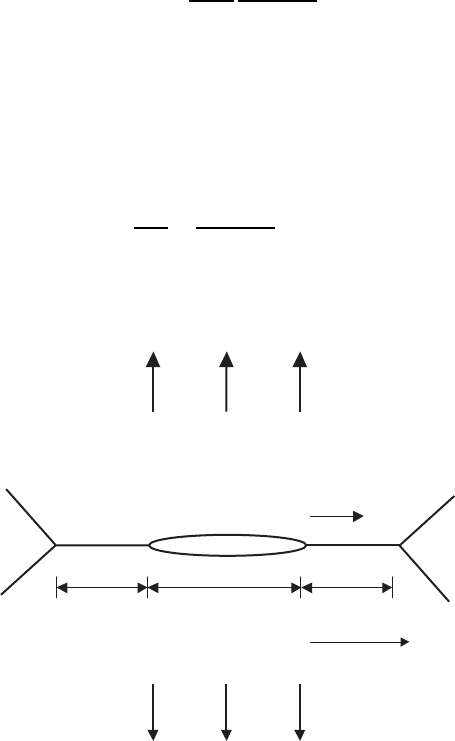
θ = s/r

•

(s, θ)

Fig. 4.14. Illustration of crack tip proﬁle, indicating crack tip angle, 2φ,andpolar

coordinates (s, θ)

of the local equilibrium at the crack tip is that the crack must be screened

by dislocation ﬁeld and maintains a dislocation-free zone with the size d.The

loaded system “crack–dislocation arrays” maintains a local stress, σ

,inthe

dislocation-free zone and produces the next stress intensity in the screening

dislocation zone, given by Hutchinson–Rice–Rosengren model as [884]

= σ

a<|x| <a+ d (4.46)

= βσ

/σ

)

2n/(n+1)

(|x|−a)

−n/(n+1)

a + d<|x| <a+ d + r

(4.47)

where K

is the applied stress intensity and β is the factor, which depends on

the elastic and plastic deformation properties (see Fig. 4.15).

The carbon segregation process is found by the crack tip proﬁle and by

the stress ﬁeld ahead of the crack tip. The chemical potentials of carbon and

superconductor can be stated, following [507] in various grain boundary and

crack surface zones, namely, I is the zone not aﬀected by the stress intensity

(|x| >a+ d + r

); II is the zone of screening dislocations (a+d<|x| <a+ d +

); III is the dislocation-free zone ahead of the crack tip (a<|x| <a+ d);

IV is the arc-shaped crack tip zone (a − q<|x| <a); and V is the parallel

ﬂat crack surface zone (|x| <a− q).

At equilibrium, the chemical potentials of carbon and superconductor must

be the same in all the regions, respectively. So, the equilibrium carbon segre-

gation depends on the binding energies and crack tip conditions. The binding

energies of carbon at grain boundaries and crack surfaces (H

)

and (H

)

respectively, are found through the standard chemical potentials of C and

HTSC as

)

=(μ

)

− (μ

)

− (μ

)

HTSC

+(μ

)

HTSC

; (4.48)

)

=(μ

)

− (μ

)

− (μ

)

HTSC

+(μ

)

HTSC

. (4.49)

Here and further the subscript m is the matrix, b is the grain boundary and

s is the crack surface.

4.4 Modeling of Carbon Segregation and Fracture Processes of HTSC 211

ξ (=x – a)

(x)

VIV

III

II I

Fig. 4.15. Illustration of local stress and stress intensity ahead of the dislocation-

screened crack tip and deﬁnition of various regions, where diﬀerent chemical poten-

tials are given

The basic assumption of the model is that the embrittlement occurs as

a reduction of the surface and grain boundary energies due to the carbon

segregation. Moreover, it is taken into account that slow fracture occurs when

the solute is suﬃciently rapid to maintain the same chemical potential of

solute between the grain boundary and the crack surface. Fast fracture occurs

when the solute concentration remains the same at the grain boundary and

the crack surface. Then, from the thermodynamic theory proposed by Seah,

Rice and Hirth, the ideal works, expended in slow (γ

)andfast(γ

) fracture,

can be obtained as [507]

= γ

− RT (2C

/Ω

− C

III

/Ω

) ; (4.50)

= γ

− (C

III

/Ω

)Δμ . (4.51)

Here, the equilibrium carbon concentrations in zones III and V have forms:

III

exp



)

+ σ

−

4G(1+ν)



/(RT )



1 − C

+ C

exp



)

+ σ

−

4G(1+ν)



/(RT )



; (4.52)

exp[(H

)

/(RT )]

1 − C

+ C

exp[(H

)

/(RT )]

, (4.53)

where C

is the bulk carbon concentration; V

is the molar volume of carbon;

R is the gas constant; 1/Ω

is the carbon coverage at interfaces; C

III

and C

III

are the critical values of carbon concentration in zone III, required for slow

and fast fractures, respectively; γ

is the ideal work of intergranular fracture

in the absence of carbon (= 2γ

− γ

; γ

is the surface fracture energy and

is the fracture energy of grain boundary); and Δμ = RT ln(2C

III

)is

the chemical potential diﬀerence between the crack surface and the stressed

grain boundary.

212 4 Carbon Problem

The equations for constant carbon concentrations can also be found in

zones I and IV. In this case, C

coincides with C

,inwhich(H

)

is replaced

by (H

)

,andforC

we have

exp





(1 − C

)

(1 − C

=exp{[(H

)

+ γ

/Ω

]/(RT )} , (4.54)

where r is the curvature radius of the arc-shaped crack tip (Fig. 4.14). At

the same time, due to the variable stress distribution (4.46) and (4.47), the

carbon content in zone II is not constant. The relationship between the critical

stress intensity, required to propagate the crack (for slow, fast or steady-state

fracture) and to change the ideal work due to the carbon segregation, is stated

by using the local energy balance condition as [507]

−(1 − ν)K

/2G + γ

≤ 0 , (4.55)

where the superscript c corresponds to certain fracture state, K

is the local

stress intensity factor connected with the dislocation-free zone size ahead of

the crack tip (d) and local stress (σ

) in this zone by the equation, approxi-

mately derived from the load balance condition between a crack with a linear

stress intensity and that with local stress [507]: πd =(K

/σ

)

.Moreover,

a relation between σ

and δ

follows from the condition that the elastic

energy release rate is the same as the J-integral, i.e., σ

= K

[2(1−ν

)/δ

]

1/2

Then the threshold apparent stress intensity, K

, is given by the relationships

(4.47), and (4.55):

= K

(γ

/γ

)

(n+1)/4n

(δ

/δ

)

(1−n)/4n

, (4.56)

where K

is the fracture toughness, δ

is the critical crack opening displace-

ment (CCOD), required for various fracture processes (superscript c), and δ

is the CCOD in the absence of carbon, deﬁned as

[4G(1 + ν)γ

]

(n+1)/(1−n)

[2π(1 − ν

)]

2n/(1−n)

2(n+1)/(1−n)

4n/(1−n)

. (4.57)

Note that for the crack to maintain the dislocation-free zone during the

growth, besides the inequality (4.55), it is necessary to satisfy an additional

condition, namely the total energy balance criterion in the form [507]:

−(1 − ν)K

/2G + γ

+ γ

≤ 0 , (4.58)

where γ

is the plastic work due to the generation and motion of screening

dislocations, which could be found numerically, for example, in the case of a

linear dislocation array [507, 884].

4.4 Modeling of Carbon Segregation and Fracture Processes of HTSC 213

4.4.2 Steady-State Crack Growth

Assume that the carbon diﬀusion along stressed boundaries and crack sur-

faces is the mechanism which controls the intergranular embrittlement and

aﬀects the crack growth rate. In this case, the bulk diﬀusion eﬀects on carbon-

induced intergranular cracking (CIIC) are neglected. Under the geometrical

and loading conditions of the equilibrium crack growth problem, the steady-

state case indicates subcritical intergranular crack growth with constant veloc-

ity, ν

(Fig. 4.16). Taking into account the grain boundary and crack surface

zones (II–V), the ﬂuxes of carbon in these regions, J

, can be stated as

= −

dμ

d(x or s)

, (4.59)

where D

is the diﬀusivity of carbon, C

is the carbon concentration, i is the

subscript indicating b or s and j is the superscript indicating various interface

zones; μ

are the corresponding chemical potentials. The diﬀerentiation with

respect to s is carried out only in zone IV; in this case s is the variable arc

length in the corresponding part of the arc-shaped crack tip (see Fig. 4.14).

The continuity equation of ﬂuxes is

d(x or s)

=0, (4.60)

where t is the time. Based on (4.46), (4.47), (4.59) and (4.60) and also the

relationships between the interface energies, γ

, and the amounts of carbon,

Fig. 4.16. Schematic representation of steady-state growth of intergranular crack

and boundary condition

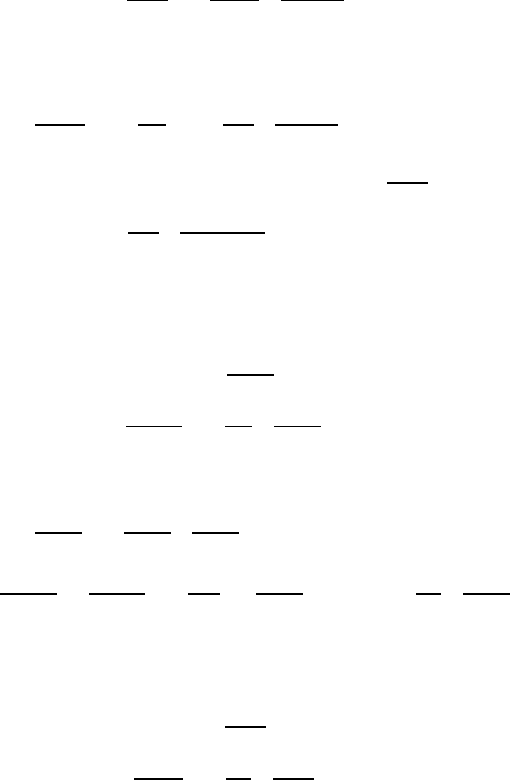
214 4 Carbon Problem

, in the various zones, derived from Gibbs theory and dilute solute ap-

proximation as γ

= γ

− (RT/Ω

, the second-order diﬀerential equations

controlling the carbon diﬀusion in the intergranular cracking regions can be

obtained, similar to [508]:

Zone II:

= −D

−





(n +1)

βσ

(1−n)/(n+1)

× K

2n/(n+1)

(x − a)

(−2n−1)/(n+1)

; (4.61)









(n +1)

βσ

(1−n)/(n+1)

×K

2n/(n+1)

(x − a)

(−2n−1)/(n+1)



−





n(2n +1)

(n +1)

βσ

(1−n)/(n+1)

× K

2n/(n+1)

(x − a)

(−3n−2)/(n+1)

=0. (4.62)

Zone III:

III

= −D

III

; (4.63)

III





III

=0. (4.64)

Zone IV:

= −D

−



rΩ



; (4.65)





rΩ





rΩ





+sec φ





=0.

(4.66)

Zone V:

= −D

; (4.67)





=0. (4.68)

The boundary values of carbon concentration, C

••

(at x =0)andC

••

(at x = a + l

) used in the solution of the second-order diﬀerential equations,

4.4 Modeling of Carbon Segregation and Fracture Processes of HTSC 215

have forms:

••

exp[(H

)

/(RT )]

1 − C

+ C

exp[(H

)

/(RT )]

; (4.69)

••

exp{[(H

)

+ σ

]/(RT )}

1 − C

+ C

exp{[(H

)

+ σ

]/(RT )}

, (4.70)

where σ

is the local stress in a triple point of intergranular boundary.

The conditions at the boundaries between zones are given by

Zones II–III:

)

x=a+d

=(C

III

)

x=a+d

; (4.71)





x=a+d





(n +1)

βσ

(1−n)/(n+1)

2n/(n+1)

(−2n−1)/(n+1)

)

x=a+d



III



x=a+d

. (4.72)

Zones III–IV (at the crack tip):

+ RT ln(C

III

)

x=a

− σ

•

•2

4G(1 + ν)

= μ

+ RT ln(C

)

s=rφ

− (V

/r){γ

− [RT (C

)

s=rφ

/Ω

]} ; (4.73)



III



x=a

=2D





)

s=rφ

rΩ





s=rφ

. (4.74)

Zones IV–V:

RT ln(C

)

s=0

− (V

/r){γ

− [RT (C

)

s=0

/Ω

]} = RT ln(C

)

x=a−q

;

(4.75)





)

s=0

rΩ





s=0





x=a−q

. (4.76)

It is assumed that the steady-state crack growth maintains the equilibrium

values at the crack center and at the triple point of grain boundaries ahead

of the crack. It should be noted that the present boundary condition is a

ﬁrst order approximation because the equilibrium content of carbon at the

triple grain junction is diﬃcult to attain, especially at suﬃciently high velocity

of thecrack. The interface conditions show that the chemical potentials and

ﬂuxes of carbon must be the same at each interface in order to maintain the

continuity of the carbon ﬂux. So, the boundary-value problem is stated for the

solution of which some relationships, deﬁned in the equilibrium crack growth,

216 4 Carbon Problem

are to be used, namely: the local equilibrium condition at the crack tip, the

geometrical crack tip conditions, and also the crack tip condition, derived from

the local energy criterion (4.55). The carbon diﬀusivity eﬀect is determined

by the ideal work of steady-state fracture as

•

= γ

− RT (2C

•

/Ω

− C

•

III

/Ω

)+(C

•

/Ω

+ C

•

III

/2Ω

)Δμ

•

, (4.77)

where

•

=(C

)

x=a−q

•

III

=(C

III

)

x=a

; (4.78)

Δμ

•

= μ

− μ

+ RT ln(C

•

III

•

) − σ

•

(σ

•

)

4G(1 + ν)

. (4.79)

The superscript • indicates the steady-state fracture. The boundary-value

problem can be solved numerically, for example, by using the Runge-Kutta

method. The boundary conditions at the triple points permit to study the

eﬀect of grain sizes on the kinetics of CIIC. At the same time, the size eﬀects

cannot be estimated in the cases of the equilibrium slow and fast cracks.

4.4.3 Some Numerical Results

Numerical results can be obtained in the case of equilibrium crack growth

for diﬀerent values of the bulk carbon concentration, C

. Equating the right

parts of the (4.46), and (4.47) at |x| = a + d and K

= K

and consider-

ing the relations (4.50), (4.52), (4.53) and (4.55) for slow crack and (4.51),

(4.52), (4.53) and (4.55) for fast crack, the problem is reduced to numerical

solution of transcendental algebraic equations. These equations state the re-

lationships γ

and the critical tip conditions (σ

,δ

)toC

. Then, the values

of K

are determined from (4.56), using the calculated values of γ

and δ

Based on test data, the necessary parameters for numerical calculations are

=1J/m

,1/Ω

=1/Ω

=8.1×10

−5

mol/m

,(H

)

=50kJ/mol, (H

)

10 kJ/mol,n =0.1, σ

=10MPa,V

=2× 10

−6

/mol, R =8.316 J/mol K,

ν =0.2, K

=1MPam

1/2

, G =50GPa,T = 1110 K. The numerical results

are presented in Tables 4.2 (slow crack) and 4.3 (fast crack) [812].

As shown by the numerical results, all auxiliary parameters (d

,σ

,δ

) change monotonously with C

for both slow and fast fractures. In

particular, the normalized parameter, γ

/γ

, decreases with an increase of

. At the same time, the normalized parameter, δ

/δ

, increases along with

. These alternative contributions to K

cause its non-monotonous

behavior in the dependence on C

. In this case, the strengthening eﬀect on

(i.e., when K

> 1) occurs when the segregation of carbon in the

crack regions strongly aﬀects the crack tip condition (i.e., reduction of δ

but does not produce a substantial reduction in γ

(see (4.56)). More evident

change of all auxiliary parameters in the case of slow crack compared with the

4.4 Modeling of Carbon Segregation and Fracture Processes of HTSC 217

Table 4.2. Numerical results for slow crack

Parameters C

(ppm)

50 100 150 200 250 300

(μm) 185 176 167 159 150 142

/σ

1.438 1.444 1.451 1.458 1.465 1.472

0.347 0.340 0.332 0.326 0.318 0.311

/γ

0.963 0.925 0.882 0.850 0.809 0.774

/δ

1.050 1.104 1.164 1.222 1.295 1.368

1.007 1.007 0.996 1.004 0.999 0.999

fast crack at the considered range of C

proposes the greater susceptibility of

slow growth on CIIC increase. Then, it is apparent that under the condition

of a dislocation-screened crack, carbon segregation induces slow fracture more

readily than fast fracture. The weak change of K

on C

in both cases

of slow and fast cracks is apparently caused by the small range of C

(while

this is a real bulk carbon concentration in HTSC systems). The presented

numerical example should be speciﬁed with more accurate selection of key

parameters for certain HTSC.

For the used local energy criterion, which is controlled by CIIC, the de-

pendence of K

on the ideal work of fracture, the crack tip conditions and

the plastic deformation properties (see (4.56)) is somewhat similar to that ob-

tained in [1137]. The diﬀerence is that the present analysis explicitly includes

not only the embrittlement eﬀect of carbon, but also the crack tip conditions,

aﬀected by the carbon segregation. It should be noted that the presence of

a dislocation-screened crack and the microscopic behavior of plastic defor-

mation, associated with CIIC, have not yet been experimentally veriﬁed in

HTSC compositions. However, as has been known, an intergranular crack

remains atomistically sharp when an energy barrier for the nucleation of a

dislocation loop at a crack tip is present. This barrier is produced due to a

low level of stress intensity at the crack tip in the presence of screening disloca-

tions, stated by the dislocation sources (e.g., such as intergranular boundaries,

Table 4.3. Numerical results for fast crack

Parameters C

(ppm)

50 100 150 200 250 300

(μm) 188 182 176 169 163 157

/σ

1.436 1.440 1.444 1.450 1.454 1.459

0.349 0.344 0.340 0.334 0.329 0.324

/γ

0.974 0.947 0.925 0.892 0.866 0.840

/δ

1.034 1.067 1.104 1.150 1.192 1.238

1.002 0.997 1.007 1.000 1.000 1.000