Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica
Подождите немного. Документ загружается.


© 2001 by CRC Press LLC
(2)
where L is the length of the beam. The problem is to determine the resulting
deflection y(x). Knowing y, the moment and shearing force, V, distributions can
subsequently be determined based on Equation 1 and V = dM/dx. The final objective
is to calculate the stress distributions in the loaded beam using the M and V results.
The Runge-Kutta method for solving an initial problem can be applied here if
in additional to the initial condition given in (2), y(x = 0) = 0, we also know the
slope, , at x = 0. But, we can always make a guess and hope that by making better
and better guesses the trial process will eventually lead to one which satisfies the
other boundary condition, namely y(x = L) = 0 given in Equation 3. In fact, if the
problem is linear, all we need to do is making two guesses and linearly combine
these two trial solutions to obtain the solution y(x).
Let us first convert the governing differential Equation 1 into two first-order
equations as:
(3,4)
To apply the fourth-order Runge-Kutta method, we have to first decide on a
stepsize h, for example h = L/N we then plan to calculate the deflections at N + 1
locations, x + jh for j = 1,2,…N since j = 0 is the initial location. If we assume a
value for
0
, say A, the Runge-Kutta process will be able to generate the following
table
FIGURE 8. The problem of a loaded beam.
x0h 2h…jh…Nh
x
1
=y
(1)
0y
1
(1)
y
2
(1)
…y
j
(1)
…y
N
(1)
(5)
x
2
=θ
(1)
A θ
1
(1)
θ
2
(1)
… θ
j
(1)
… θ
N
(1)
yx and yx L=
()
==
()
=00 0
dx
dx
xxx yx
dx
dx
M
EI
xx x
1
21
2
20
000
00
==
()
==
()
=
==
()
==
()
=
,
, θθ

© 2001 by CRC Press LLC
If y
N
(1)
= 0, then the value A selected for (x = 0) is correct and the y and
values listed in Equation 5 are the results for the selected stepsize. If y
N
(1)
is not
equal to zero, then the value incorrectly selected, we have to make a second try by
letting (x = 0) = B to obtain a second table by application of the Runge-Kutta
method. Let the second table be denoted as:
Again, if y
N
(2)
= 0, then the value B selected for θ(x = 0) is correct and the y and
θ values listed in Equation 6 are the results for the selected stepsize. Otherwise, if
the problem is linear, the solutions can be obtained by linearly combining the two
trial results as, for j = 1,2,…,N:
(7,8)
where the weighting coefficients and are to be determined by solving the equations:
(9,10)
Equation 10 is derived from the boundary condition y(x = Nh = L) = 0 and based
on Equation 7. Equation 9 needs more explanation because it cannot be derived if
y(x = 0) = 0. Let us assume that for the general case, y(x = 0) = . Then Equation
7 gives + = which leads to Equation 9. Using Cramer’s rule, we can easily
obtain:
(11,12)
and
(13)
NUMERICAL EXAMPLES
Let us consider the problem of a loaded beam as shown in Figure 8. The
crosssection of the beam has a width of 1 cm and a height of 2 cm which results in
a moment of inertia I = 2/3 cm
4
. The reactions at the left and right supports can be
computed to be 5/3 N and 25/3 N, respectively. Based on these data, it can be shown
that the equations for the internal bending moments are:
(14)
x0h 2h…jh…Nh
x
1
=y
(2)
0y
1
(2)
y
2
(2)
…y
j
(2)
…y
N
(2)
(6)
x
2
=θ
(2)
B θ
1
(2)
θ
2
(2)
… θ
j
(2)
… θ
N
(2)
Y y y and
jj j jj j
=+ =+
() ( ) () ( )
αβ θαθβθ
12 12
αβ α β+= + =
() ( )
10
12
and y y
NN
αβ==−
() ()
y D and y D
NN
21
Dy y
NN
=−
()
(2
1
Mx
x for x cm
x x for x cm
()
=
≤≤
−+ − <≤
53 0 20
200
65
3
1
2
20 30
2
,
,

© 2001 by CRC Press LLC
If the beam has a Young’s modulus of elasticity E = 2x10
7
N/cm
2
, we may decide
on a stepsize of h = 1 cm and proceed to prepare a computer program using the
fourth-order Runge-Kutta method to generate two trial solutions and then linearly
combining to arrive at the desired distributions of the deflected shape y(x) and slope
(x). The FORTRAN version of this program called OdeBvpRK to be presented
later has produced the following display on screen:

© 2001 by CRC Press LLC
FORTRAN VERSION
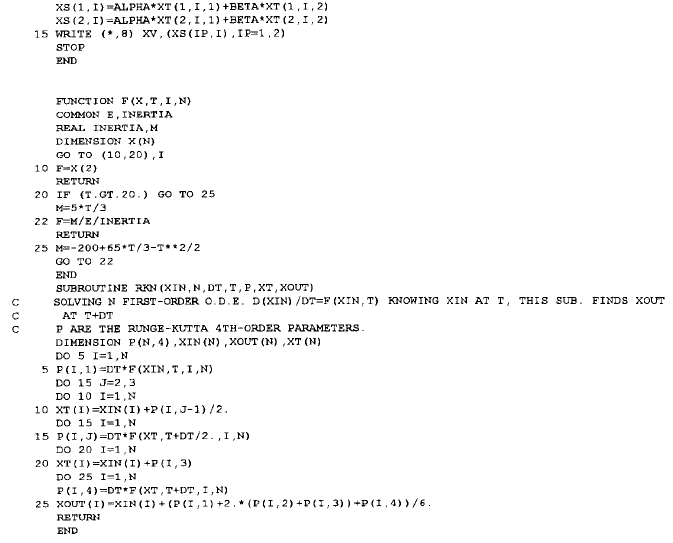
© 2001 by CRC Press LLC
The Subprogram FUNCTION F which defines the initial-value problem is coded
in accordance with Equation 14. The two trial initial slopes are selected as equal to
0.1 and 0.2. The trial results are kept in the three-dimensional variable XT, in which
the deflection y
(k)
(j) for the kth try at station x = x
j
= jh is stored in XT(1,j,k) whereas
the slope there is stored in XT(2,j,k) for j = 1,2,…,30 and k = 1,2. Such a three-
subscripts arrangement facilitates the calling of the subroutine RKN because
XT(1,KS,NTRY) is transmitted as XIN(1) and automatically the next value
XT(2,KS, NTRY) as XIN(2), and the computed results XOUT(1) and XOUT(2) are
to be stored as XT(1,KS + 1,NTRY) and XT(2,KS + 1,NTRY), respectively. Notice
that there are only two dependent variables, NV = 2.
After the weighting coefficients (ALPHA in the program) and (BETA) have
been calculated, the final distributions of the deflection and slope are saved in first
and second rows of the two-dimensional variable X, respectively. It should be
emphatically noted that the solutions obtained is only good for the selected stepsize
h = 1 cm. Whether it is accurate or not remains to be tested by using finer stepsizes
and by repeated application of the Runge-Kutta methods.
It can be shown that the maximum deflection of the loaded beam is equal to
–2.019 cm and is obtained when the stepsize is continuously halved and two con-
secutively calculated values is different less than 0.0001 cm in magnitude. The
needed modification of the above listed program to include this change in the stepsize
and testing of the difference in the maximum deflection is left as homework for the
reader.

© 2001 by CRC Press LLC
QUICKBASIC VERSION
MATLAB APPLICATIONS
In the program RungeKut, MATLAB is used for solving initial value problems
by application of its m function ode45 based on the fourth- and fifth-order Runge-
Kutta method. Here, this function can be employed twice to solve a boundary-value
problem governed by linear ordinary differential equations. To demonstrate the
procedure, the sample problem discussed in FORTRAN and QuickBASIC versions
of the program OdeBvpRK, with the aid of function BVPF.m listed in the subdi-
rectory <mFiles>, can be solved by interactive MATLAB operations as follows:

© 2001 by CRC Press LLC
Notice that format compact enables the display to use fewer spacings; YT1 and
YT2 keep the two trial solutions, and ode45 automatically determines the best
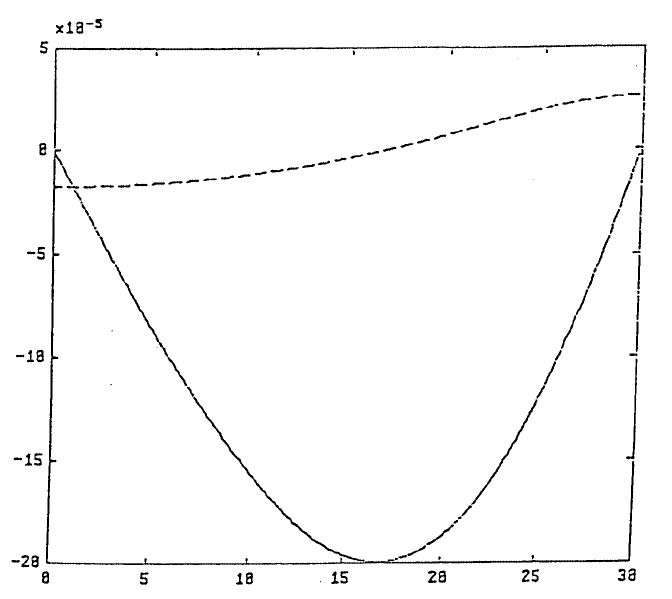
stepsize which if used directly will result in a coarse plot as shown in Figure 9. The
plot showing solid-line curve for the deflection and broken-line curve for the slope
can, however, be refined by linear interpolation of the data (X,Yanswer) and expand-
ing X and the two columns of Yanswer into new data arrays of XSpline, YSpline,
and YPSpline, respectively. Toward that end, the m function spline in MATLAB is
to be applied as follows:

© 2001 by CRC Press LLC
The result of plotting the spline curves is shown in Figure 10.
MATHEMATICA APPLICATIONS
The Runge-Kutta method, particularly the most popular fourth-order method,
can be applied for solution of boundary-value problem governed by ordinary differ-
ential equation(s). Here, only the application of this method is elaborated; readers
are therefore referred to program RungeKut to review the method itself and the
development of related programs and subprograms. The boundary-value problem is
to be solved by continuously guessing the initial condition(s) which are not provided
until all boundary conditions are satisfied if the problem is nonlinear. When the
problem is linear, then only a finite number of guesses are necessary. A system of
two first-order ordinary differential equations which governed the loaded elastic
beam problem previously solved in the MATLAB application is here adapted to
demonstrate the application of the Runge-Kutta method.
FIGURE 9.
© 2001 by CRC Press LLC
In[1]: = EI = 4.*10^7/3; F[X_] = If[X>20,
(–200 + 65*X/3X^2/2)/EI, 5*X/3/EI]
In[2]: = Id1 = (NDSolve[{Y[X] = = YP[X], YP'[X] = = F[X], Y[0] = = 0,
YP[0] = = 0.1}, {Y,YP}, {X, 0, 30}])
In[3]: = Y30Trial1 = Y[30]/. Id1
Out[3] = {3.00052}
EI value and F(X) are defined in In[1]. In[2] specifies the two first-order ordinary
differential equations involving the deflection Y and slope YP, describes the correct
initial condition Y(X = 0) = 0, gives a guessed slope Y(X = 0) = 0.1, and decides
on the limit of investigation from X = 0 to X = 30. In[3] interpolates the ending Y
value by using the data obtained in Id1. A second trial is then to follow as:
In[4]: = Id2 = (NDSolve[{Y[X] == YP[X], YP'[X] = = F[X],
Y[0] == 0, YP[0] == 0.2},
{Y,YP}, {X, 0, 30}])
FIGURE 10. The result of plotting the spline curves.
© 2001 by CRC Press LLC
In[5]: = Y30Trial2 = Y[30]/. Id2
Out[5] = {6.00052}
Linear combination of the two trial solutions is now possible by calculating a
correct Y(X = 0) which should be equal to the value given in Out[8].
In[6]: = d = Y30Trial2Y30Trial1; a = Y30Trial2/d; b = -Y30Trial1/d;
In[7]: = Print[“Alpha = “,a,” Beta = “,b]
Out[7] = Alpha = {2.00017} Beta = {–1.00017}
In[8]: = YP0 = 0.1*a + 0.2*b
Out[8] = {–0.0000174888}
Finally, the actual deflection and slope can be obtained by providing the correct
set of initial conditions and again applying the Runge-Kutta method.
In[9]: = Id = (NDSolve[{Y[X] = = YP[X], YP'[X] = = F[X],
Y[0] = = 0, YP[0] = = –0.0000174888},
{Y,YP}, {X,0,30}])
In[10]: = (Do[Print[“X = “, Xv, “ Y = “, Y[Xv]/.Id, “ DY/DX = “,
YP[Xv]/.Id], {Xv,0,30}])
Out[10] =
X = 0 Y = {0.} DY/DX = {–0.0000174888}
X = 1 Y = {–0.0000174645} DY/DX = {–0.0000174262}
X = 2 Y = {–0.0000348041} DY/DX = {–0.0000172387}
X = 3 Y = {–0.0000518936} DY/DX = {–0.0000169262}
X = 4 Y = {–0.0000686077} DY/DX = {–0.0000164887}
X = 5 Y = {–0.0000848222} DY/DX = {–0.0000159262}
X = 6 Y = {–0.000100412} DY/DX = {–0.0000152387}
X = 7 Y = {–0.000115251} DY/DX = {–0.0000144262}
X = 8 Y = {–0.000129215} DY/DX = {–0.0000134887}
X = 9 Y = {–0.00014218} DY/DX = {–0.0000124262}
X = 10 Y = {–0.000154019} DY/DX = {–0.0000112387}
X = 11 Y = {–0.000164608} DY/DX = {–0.00000992619}
X = 12 Y = {–0.000173788} DY/DX = {–0.00000848869}
X = 13 Y = {–0.000181454} DY/DX = {–0.00000692619}
X = 14 Y = {–0.000187493} DY/DX = {–0.00000523869}
