Ожигов Ю.С. Квантовые вычисления
Подождите немного. Документ загружается.


χ
i
= b
i
|e
1
e
2
i + a
i
|e
1
N
2
i + α
i
|N
1
N
2
i + β
i
|N
1
e
2
i,
e
1
e
1
, e
2
f
1
(x) = 1 f
2
(x, y) = 1
N
1
=
N
P
i=2
e
i
, N
2
=
P
i6=2
e
i
χ
i
−→ Z(χ
i
)
χ
i
1
−→ Z
1
(χ
i
) = χ
0
i
2
−→ Z
2
(χ
0
i
) = χ
i+1
,
Z
1
= −W
y
R
0y
W
y
F
2
, Z
2
= −W
x
R
0x
W
x
F
1
.
Z
1
Z
2
x y
χ
0
i
χ
0
i
= b
0
i
|e
1
e
2
i + a
0
i
|e
1
N
2
i + α
0
i
|N
1
N
2
i + β
0
i
|N
1
e
2
i.
x x = e
1
x+e
j
, j 6=
1
W R
0
W λ
av
x = e
1
λ
av
=
(N−1)a
i
−b
i
N
, b
0
i
= 2λ
av
+ b
i
a
0
i
= 2λ
av
− a
i
b
0
i
=
2(N−1)a
i
−2b
i
N
+ b
i
= b
i
(1 −
2
N
) + 2a
i
(1 −
1
N
),
a
0
i
=
2(N−1)a
i
−2b
i
N
− a
i
= −b
i
2
N
) + a
i
(1 −
2
N
).
x = e
j
, j 6= 1
λ
av
=
(N−1)α
i
+β
i
N
, α
0
i
= 2λ
av
− α
i
β
0
i
= 2λ
av
− β
i
α
0
i
=
2(N−1)α
i
+2b
i
N
− a
i
= α
i
(1 −
2
N
) + 2β
i
2
N
),
β
0
i
=
2(N−1)α
i
+2β
i
N
− β
i
= α
i
(1 −
1
N
) − β
i
(1 −
2
N
).
χ
0
i
2
−→ Z
1
(χ
0
i
) = χ
i+1
.
y : y = e
2
y = e
j
, j 6= 2
y = e
2
λ
av
=
(N − 1)β
0
i
− b
0
i
N
,
b
i+1
= 2λ
av
+ b
0
i
= b
0
i
(1 −
2
N
) + 2β
0
i
(1 −
1
N
),
β
i+1
= 2λ
av
− β
0
i
= β
0
i
(1 −
2
N
) − b
0
i
2
N
.
y = e
j
, j 6= 2
λ
av
=
(N − 1)α
0
i
− a
0
i
N
,
a
i+1
= 2λ
av
+ a
0
i
= a
0
i
(1 −
2
N
) + 2α
0
i
(1 −
1
N
),
α
i+1
= 2λ
av
− α
0
i
= α
0
i
(1 −
2
N
) − a
0
i
2
N
.

b
i+1
= b
i
(1 −
2
N
)
2
+ 2a
i
(1 −
1
N
)(1 −
2
N
) + 4α
i
(1 −
1
N
)
2
− 2β
i
(1 −
2
N
)(1 −
1
N
);
a
i+1
= a
i
(1 −
2
N
)
2
− b
i
2
N
(1 −
2
N
) + 2α
i
(1 −
2
N
)(1 −
1
N
) + 2β
i
2
N
(1 −
1
N
);
α
i+1
= α
i
(1 −
2
N
)
2
+ β
i
2
N
(1 −
2
N
) − a
i
(1 −
2
N
)
2
N
+ b
i
4
N
2
;
β
i+1
= 2α
i
(1 −
1
N
)(1 −
2
N
) − β
i
(1 −
2
N
)
2
− b
i
(1 −
2
N
)
2
N
− 2a
i
(1 −
1
N
)
2
N
.
Z =
1 2 4 −2
−
2
N
1 2
4
N
4
N
2
−
2
N
1
2
N
−
2
N
4
N
2 −1
.
b
i+1
− b
i
= 2a
i
+ 4α
i
− 2β
i
+ b
i
O
1
(
1
N
) + a
i
O
2
(
1
N
) + α
i
O
3
(
1
N
) + β
i
O
4
(
1
N
);
a
i+1
− a
i
= −
2
N
b
i
+ 2α
i
+ a
i
O
5
(
1
N
) + b
i
O
6
(
1
N
2
) + α
i
O
7
(
1
N
) + β
i
O
8
(
1
N
);
α
i+1
− α
i
= −
2
N
a
i
+ β
i
O
13
(
1
N
) + a
i
O
14
(
1
N
2
) + b
i
O
15
(
1
N
2
) + α
i
O
16
(
1
N
);
β
i+1
− β
i
= −
2
N
b
i
+ 2α
i
− 2β
i
+ a
i
O
9
(
1
N
) + α
i
O
10
(
1
N
) + β
i
O
11
(
1
N
) + b
i
O
12
(
1
N
2
).
{¯c
i
} C
k
: ¯c
i
= (c
1
i
, c
2
i
, . . . , c
k
i
), c
j
i
∈ C
¯c
i+1
− ¯c
i
= A¯c
i
,
A k × k
m C(t) : R −→ C
k
˙
C(t) = mAC(t)
C(0) = ¯c
0
.
C(t) = R(t)¯c
0
, R(t) =
exp(mAt) C(t)
¯c
i
C(i/m), i = 0, 1, . . . .
C(
i+1
m
) = C(
i
m
) +
1
m
˙
C(
i
m
) +
1
2m
2
¨
C(t
1
),
i
m
<
t
1
<
i+1
m
1
1
2m
2
¨
C(t
1
) =
1
2
A
2
C(t
1
)
1
2
A
2
exp(mAθ
1
)¯c
0
1
2
A
2
exp(mAθ
2
)¯c
1
+
exp(mA
1
m
)
1
2
A
2
exp(mAθ
1
)¯c0 =
1
2
A
2
exp(mAθ
2
)(¯c
0
+A¯c
0
+
1
2
A
2
exp(mAθ
1
)¯c
0
)+exp(A)
1
2
A
2
exp(mAθ
1
)¯c
0
i
i
≤
3
2
P
j=1
i exp(Aα
j
)A
2
¯c
0
0 < α
j
< 1 k¯c
0
k ≤ h
i
i
= O(ih) kc
0
k = O(
1
N
)
i = o(N)
i = O(
√
N) N

B(τ) B(tm) = C(t) B
d
dτ
B(τ) = AB(τ ), B(0) = c
0
.
¯c
i
= |b
i
, a
i
, α
i
, β
i
i ¯c
0
= |
1
N
,
1
N
,
1
N
,
1
N
i
B = |b, a, α, βi b, a, β, α B t
˙
b = 2a + 4α − 2 β + bO
1
(
1
N
) +
1
+ aO
0
(
1
N
);
˙a = −
2
N
b + 2α +
2
+ O
2
(
1
N
)a;
˙
β = −
2
N
b + 2α − 2β +
4
+ O
4
(
1
N
)a;
˙α = −
2
N
a +
3
,
i
= aO
0i
(
1
N
2
) + bO
1i
(
1
N
2
) + βO
2i
(
1
N
) + αO
3i
(
1
N
), i = 1, 2, 3, 4,
b(0) = a(0) = β(0) = α(0) =
1
N
.
t = O(
√
N), i = [t]
¯
δ =
¯
B(t) − ¯c
i
= O(1/
√
N), N −→ ∞
b(i) ≈ b
i
b
i
|e
1
, e
2
i
0 ≤ t ≤ O(
√
N).
˙
B = MB M = Z − 1 =
˜
A
0
+ E + H 1
˜
A
0
=
0 2 4 0
−
2
N
0 2 0
0 −
2
N
0 0
0 0 0 0
, E =
0 0 0 0
0 0 0 0
0 0 0 0
−
2
N
0 2 −2
, H =
d
1
d
1
d
1
−2 + d
1
d
2
d
1
d
1
d
1
d
2
d
2
d
1
d
1
d
2
d
1
d
1
d
1
,
d
l
O(N
−l
), l = 1, 2.
˜
A
0
E H
R(t)
˙
R = M R R(0) = 1
C(t) = RC(0) R exp(Mt)
˜
A
0
, E, H
E H
M
˙
C(t) = AC(t) C(0) = c
0
A
0
A
0
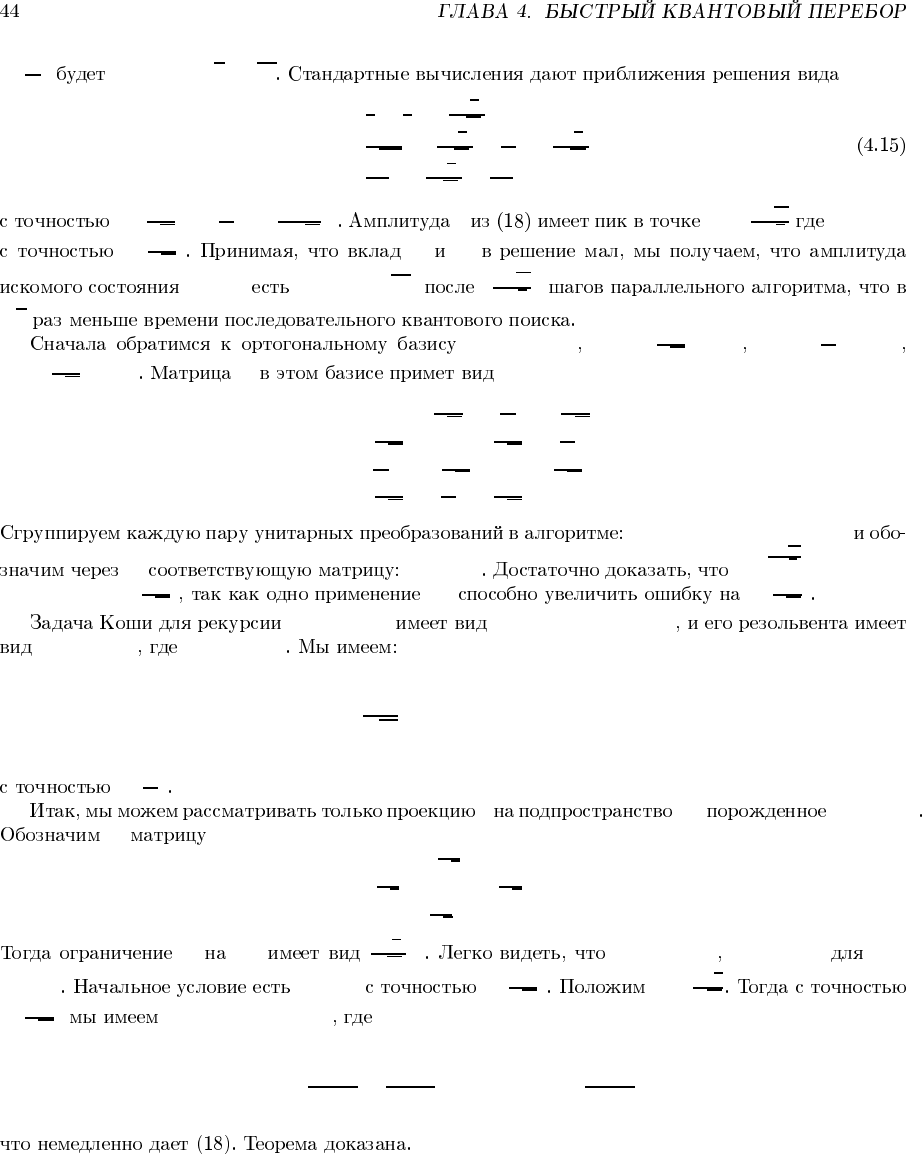
λ
3
+
8
N
λ−
16
N
2
= 0
O(
1
N
) λ
1,2
=
+
− 2
√
2i/
√
N
b =
1
2
−
1
2
cos
2
√
2t
√
N
,
a =
1
√
2N
sin
2
√
2t
√
N
+
1
N
cos
2
√
2t
√
N
,
α =
1
2N
cos
2
√
2t
√
N
+
1
2N
|O(
1
√
N
), O(
1
N
), O(
1
N
√
N
)i b t
1
=
π
√
N
2
√
2
b(t
1
) = 1
O(
1
√
N
) E H
|e
1
, e
2
i 1 − O(1/
√
N)
h
π
√
N
2
√
2
i
√
2
E
1
= |e
1
e
2
i E
2
=
1
√
N
|e
1
N
2
i E
3
=
1
N
|N
1
N
2
i
E
4
=
1
√
N
|N
1
e
2
i Z
A
1
=
1
2
√
N
4
N
−
2
√
N
−
2
√
N
1
2
√
N
4
N
4
N
−
2
√
N
1
2
√
N
−
2
√
N
4
N
2
√
N
−1
.
χ
2k
−→ χ
2k+1
−→ χ
2k+2
B B
0
= A
2
1
kB
[
π
√
N
4
√
2
]
0
|0, 0, 1, 0i−
|1, 0, 0, 0ik = O(
1
√
N
) A
1
O(
1
√
N
)
¯c
i+1
= B
0
¯c
i
˙
¯c = (B
0
−1)¯c, ¯c = ¯c
0
R = exp Bt B = B
0
− 1
B ≈
4
√
N
0 1 0 0
−1 0 1 0
0 −1 0 0
0 0 0 0
O(
1
N
)
¯c H
1
E
1
, E
2
, E
3
D
0 −
i
√
2
0
i
√
2
0 −
i
√
2
0
i
√
2
0
.
B H
1
4
√
2i
√
N
D D
2k+1
= D D
2k
= D
2
k =
1, 2, . . . |0, 0, 1i O(
1
√
N
) k =
4
√
2
√
N
O(
1
√
N
) |b, a, αi ≈ C|0, 0, 1i
C = exp(kiDt) = cos(kDt) + i sin(kDt)
= 1 −
(kDt)
2
2
+
(kDt)
4
4!
− . . . + i(kDt −
(kDt)
3
3!
+ . . .)
= 1 − D
2
(1 − cos kt) + iD sin kt

k
k χ
i
= a
i
0
|N
1
, N
2
, . . . , N
k
i+ a
i
1
|e
1
, N
2
, . . . , N
k
i +
. . . + a
i
k
|e
1
, e
2
, . . . , e
k
i + R
i
R
i
|. . . , N
p
, . . . , e
q
, . . .i
Z
k
= (−1)
k
W
(k)
R
(k)
0
W
(k)
F
(k)
,
W
(k)
= W
1
N
W
2
N
. . .
N
W
k
N
I W
i
x
i
i = 1 , 2, . . . , k
R
(k)
0
= R
01
N
. . .
N
R
0k
N
I R
0i
x
i
i = 1, 2, . . . , k F
(k)
=
F
1
N
. . .
N
F
k
N
I F
i
x
i
e
i
I
A
χ
i
= Aχ
i−1
A 2
kn
A
A
r
k + 1
|N
1
, N
2
, . . . , N
k
i, |e
1
, N
2
, . . . , N
k
i, . . . , |e
1
, e
2
, . . . , e
k
i A
r
A
r
= A
0
+ B A
0
0 2 0 . . . 0
−
2
N
0 2 . . . 0
. . . . . . . . . . . .
0 . . . −
2
N
0 2
0 . . . 0 −
2
N
0
.
−
2
N
(k+1)×(k+1) A A
r
B k > 2
˙
¯a = A¯a, a(0) = |N
−k/2
, . . . , N
−k/2
i,
¯a(i) ≈ |a
i
1
, . . . , a
i
k
i i k
√
N
∀x
1
∃y
1
∀x
2
∃y
2
. . . ∃y
k
p(x
1
, y
2
, . . . , x
k
, y
k
)
N = 2
n
x
1
y
1
. . . x
k
y
k
{0, 1}
n
O(
√
N)
(Cn)
k
C

√
N(log N)
k−1
P ∀x∃y
O(
p
|y
k
||x
1
||y
1
|. . . |x
k
|)
√
N
P
i
λ
i
e
i
e
i
e
i
ξ
χ
kχ − ξk <
f : {0, 1}
n
−→ {0, 1}
p
err
x ∈ {0 , 1}
n
ξ
0
−→ ξ
1
−→ . . . −→ ξ
T
,
ξ
0
= |x, 0i, ξ
T
= (
˜
ξ
N
|f(x)i)
, < p
err
/2, x
ξ
T
f(x) 1−p
err
P
i
λ
i
|x
i
, 0i
P
i
λ
i
˜
ξ
i
N
f(x
i
)i + ¯, ¯ =
P
i
λ
i
¯
x
i
k¯ek < p
√
N/2 N
T
O(
√
N
1
)
x p(x) p, N
1
= 2
|x|
|0, 0, . . . , 0i
|0, 0, . . . , 0, γi
p γ = 1 ∃x p(x) 0

√
N
1
Mn p M(n + 2) + 2
M = log(1/)
m
χ {1, 2, . . . , m}
W F
0
W F
p
χ
P
j
e
j
/
√
N
m =
√
N
1
x
1/2
m = 1, 2, . . .
|0 . . . 0i −→ . . . −→
1
√
m
X
χ≤m
|χi,
χ
M 2n
|0 . . . 0i
N
|x
1
x
2
. . . x
M
i
x
i
=
X
j
λ
j
e
j
,
X
p(e
j
)
|λ
j
|
2
≈ 1/2,
e
j
p
|0 . . . 0i
O
(
X
j
(λ
j
|e
j
i
O
|p(e
j
)i))
O
. . .
O
(
X
j
(λ
j
|e
j
i
O
|p(e
j
)i)),
p(e
j
) ∈ {0, 1} p
|a, bi |a, b + p(a) i
|σ
1
σ
2
. . . σ
M
0
M+2
i −→ |σ
1
σ
2
. . . σ
M
0
M+1
σi ∀i = 1, 2, . . . , M σ, σ
i
∈ {0, 1}
σ = 1 ∃i ∈ {1, . . . , M} : σ
i
= 1

f
| i
| 0 0 0 i
f
−→ | 0 0 0 i
| 0 0 1 i
f
−→ | 1 0 1 i
| 1 0 1 i
f
−→ | 1 1 1 i
| 1 0 0 i
f
−→ | 1 0 0 i
i
i
σ
i
i = 1, 2, . . . , M,
|δ
1
δ
2
. . . δ
M
δ
M+1
. . . δ
2M
σ0i |δ
1
δ
2
. . . δ
2M
σσi |σ0i −→ |σσi,
|σ
1
σ
2
. . . σ
M
0
M+1
σi
σ
1
, σ
2
, . . . , σ
M
(|0 . . . |0i
O
(
X
j
λ
j
|e
j
i
O
|p(e
j
)i))
O
. . .
O
(
X
j
(λ
j
|e
j
i
O
|p(e
j
)i))
O
γ)
.
M n
x
1 −
1
2
M
M = log
1
γ
(|0 . . . 0γi)
p p
p
z
1
, z
2
, . . . , z
q
∀x
1
∃x
2
∀x
3
. . . Q
k−1
x
k−1
Q
k
x
k
p(z
1
, z
2
, . . . , z
q
, x
1
, . . . , x
k
).
Q
1
, Q
2
∈ {∃, ∀}
| z
1
. . . z
q
0 . . . 0i −→ . . . −→ | z
1
. . . z
q
0 . . . 0γi

2
1
2
k
P
i=1
|x
k
|
(Mn)
k
z
1
, . . . z
q
γ =
0, (5) ,
1, (5) .
k k = 0
k k
2
1
2
k−1
P
i=1
|x
i
|
(Mn)
k−1
p (M n)
k−1
z
1
, . . . z
q
, x
k
−→ T
1
∈ {0, 1} T
1
= 1 ∀x
1
∃x
2
. . . Q
k−1
x
k−1
p(z
1
, . . . , z
q
, x
1
, . . . , x
k−1
, x
k
)
k−1
z
1
, . . . , z
q
−→ T ∈ {0, 1} T = 1
∀x
1
∃x
2
. . . Q
k−1
x
k−1
Q
k
x
k
p(z
1
, . . . , z
q
, x
1
, . . . , x
k
)
Q
k
∃
k−1
2
1
2
|x
k
|
Mn
k−1
2
1
2
k−1
P
i=1
|x
i
|
(Mn)
k−1
p 2
1
2
k
P
i=1
|x
1
|
(Mn)
k
p (Mn)
k
Q
k
∀
k−1
0 −→ 1, 1 −→ 0
m
N
1
N
2
π
f(x) = 1 m − 2 N
3
, N
4
, . . . , N
m
m − 2 d
1
, d
2
, . . . , d
m−2
N
s
N
s
= {x
j
s
; j = 1, 2, . . . , l
s
} s = 1, 2, . . . , m
x
1
2
, x
2
2
, . . . , x
l
2
2
m
P
s=1
l
s
= N
H H
¯
N

U I
tar
U H x
s
j
s = 1, 2, . . . , m, j =
1, 2, . . . , l
s
x
2
j
−1 x
1
j
1
x
s
j
s ≥ 3 e
i(d
k
−π)
, d
k
∈ [0, 2π) v
k
= e
id
k
k d
k
d = d
k
γ =
q
l
2
N
γ −→ 0 (n −→ ∞)
e
j
=
1
√
l
j
P
x∈N
j
|xi e
2
˜
0
1
√
N
P
x∈
¯
N
|xi
H
0
e
j
m
˜
0
I
tar
H
0
I
e
2
H
0
l
1
/N −→ 1 (N − l
1
− l
2
)/d
√
Nl
2
−→ 0
q
l
2
N
= o(d) t =
π
4
q
l
2
N
I
˜
0
U
˜
0 t
e
2
n −→ ∞
H
0
I
˜
0
U
G = −I
˜
0
U
I
˜
0
I
tar
H
0
e
2
˜
0 G
G
e
1
e
2
e
1
, e
2
, . . . , e
m
H
0
h
˜
0|e
2
i =
q
l
2
N
= X
h
˜
0|e
j
i =
q
l
j
N
= Y
j−2
j = 3, 4, . . . , n x
j
= 2X
j
m
P
j=2
l
j
/N
