Острейковский В.А. Лабораторный практикум по информатике

Подождите немного. Документ загружается.

введите с клавиатуры Х[1= нажмите

<Enter>.

На экране появится

XI =

значение первого корня;

введите с клавиатуры Х[2= нажмите

<Enter>.

На экране появится

Х2= значение второго корня;

так же получите и значения третьего корня.

Работа № 2. Построение графиков функций

Цель работы: освоить построение графиков функций в декартовой

системе координат.

4 1

Задание: требуется построить графики функций f(x):=

—

g(x):-

—,

х х

при изменении х от -10 до +10 с шагом 0,5.

Методика выполнения работы

Выведите на экран панели инструментов, необходимые для ра-

боты:

для вывода панели 1 выполните команду F10 -» View -> Math

Palette;

щелчком мыши на третьей слева пиктограмме панели 1 выведи-

те на экран панель 3 — Math Palette (Графика) для работы с графи-

ками;

щелчком мыши на первой пиктограмме панели 1 выведите на эк-

ран панель 4 — Arithmetic Palette (Счет), предназначенную для набора

различных математических формул (рис. 8.3).

Установите курсор на рабочем поле и введите с клавиатуры:

f(x):-Alx. Нажмите клавишу <Enter>. На экране появится: f(x):=—.

Формирование вектора значений: введите с клавиатуры: х:-10; 10.

Нажмите клавишу

<Enter>.

На экране появится: х: = -10..10. При такой

записи шаг изменения аргумента берется по умолчанию равным 1.

Если такая точность не устраивает пользователя, то указывается пер-

вое (минимальное) значение аргумента, затем через запятую — второе

значение аргумента, равное первому значению плюс шаг, а затем по-

сле нажатия клавиши точка с запятой (;) верхний предел диапазона из-

менения аргумента х. Так, для задания шага изменения аргумента рав-

ного 0.5, необходимо набрать х: =-10,-9.5;10.

280

!|Й+1ЁШ№М

—^

jyj^

Math Palette

•e(

Graph Palette

^НННН|Н|^^НТ

leg

tan

cos

...

Arithmetic Palette

Рис.

8.З. Панели инструментов, используемые при построении графиков функций

Построение графика начинается с вывода на экран дисплея заго-

товки графика — двух вложенных прямоугольников с черными квад-

ратиками у левой и нижней сторон (рис. 8.4):

щелкните мышью в рабочей области экрана в предполагаемой точ-

ке расположения верхнего левого угла рисуемого графика;

щелкните на кнопке Графики панели инструментов 3 Graph Palette

(или выберите команду Graph, X-Y Plot в меню Insert, или нажмите

<Shift>+<2>).

Заполните заготовку графика именем функции и именем аргу-

мента:

щелчком мыши установите курсор в точку Функция f(x) — чер-

ный квадратик у левой стороны прямоугольника;

наберите f(x);

щелчком мыши установите курсор в точку Аргумент X — черный

квадратик у нижней стороны прямоугольника;

наберите х;

нажмите клавишу

<Enter>.

График появится на экране (рис. 8.5).

6. Для оформления графика координатными осями выполните сле-

дующее:

дважды щелкните мышью на графике — появится диалоговое окно

Formatting Currently Selected X-Y Plot;

выберите вкладку X-Y Axes (рис. 8.6);

в поле выбора Axes Style нажмите кнопку Crossed для представле-

ния графика с изображением осей координат;

в поле X-Axis уберите флажок Auto

Grid,

в поле ввода Number of

Grids введите число 5, что означает разметку оси X;

281

I Ф У И К Ц Н Я f(JE) f. .

—j Аргументу |

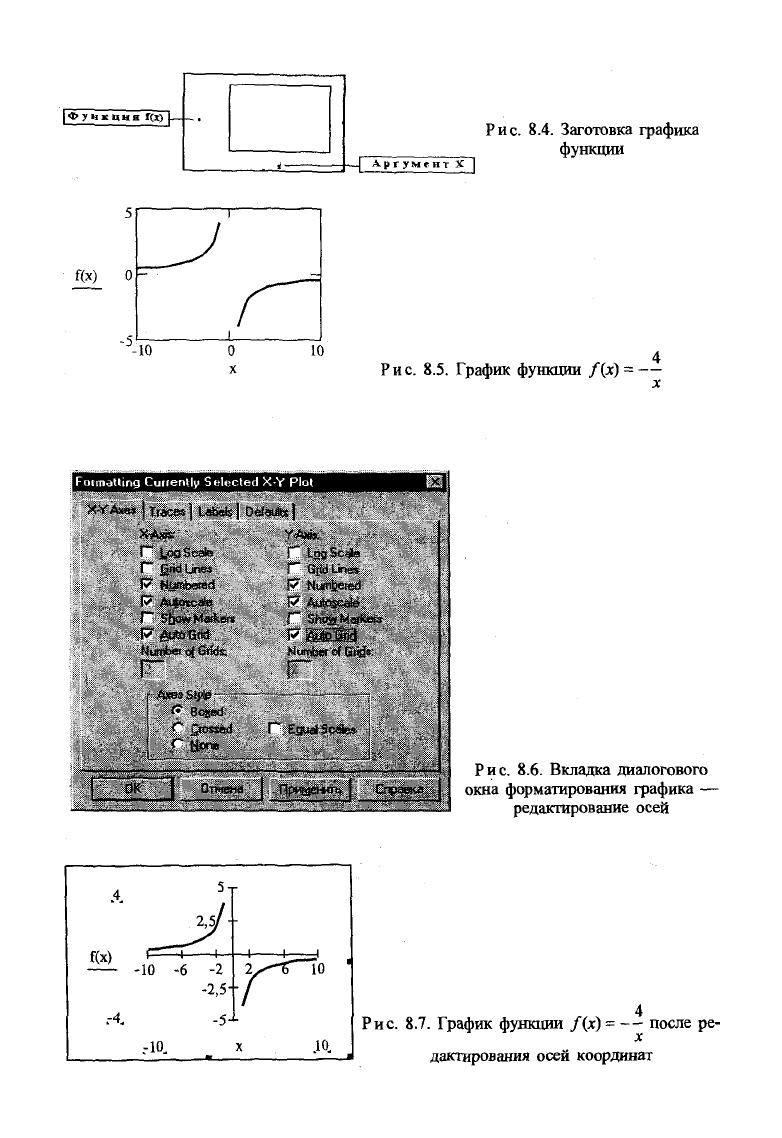
Рис.

8.4. Заготовка графика

функции

ft»

Рис.

8.5. График функции f(x) - —

FoimaMing Cuicentlv

elected XY Plot Ш1

Х-1ГАм»|Т(ас1в] Labels |

XAe

Г" Log Scab

Г* find Lines

P* Numoered

P А|4ока1в

Г" Show Markers

P £(A>Gnd

Numbei of Gitds:

**es Style

**• Bo»ed

f grossed

' Г More

DK | Отмена

Defaults |

VAKB

Г"

Log.

Scale

Г" Gnu Liners

!7 NutnQeied

17 Autosrale

Г" ShowMaifce»

^ЙЙрШ

Numbet of Gnds

P tgual Scales

1 Применить j Справка

Рис.

8.6. Вкладка диалогового

окна форматирования графика —

редактирование осей

К»

гЮ.

.10.

Рис.

8.7. График функции f(x) = — после ре-

дактирования осей координат

Formatting Currently Selected X-Y Plot

• 4 wes Ггз::: j

L«l.

UCJW-S

Lewie Label

lia:e 2

Iis.e3

iiai.i3 4

tijces

г»-*

••a e

Cymbal

пчге

TiuTft.

riLr

•;

fifW

jn*

CoJor Jvpe

it :<u

Ьгя*

ia^r эт lues

Jjdo*

Tjg inec

nAd Co ti»'

*5t i" br,e

-ЦИЕ:

W«qt.'

•fj

• 1

-A\

H.JeAjyiTrf*

t'-jr-.

Отг.чмз Г,, точить Cra

JS*

Рис.

8.8. Вкладка диалогового

окна форматирования графика —

изменения вида графика

в поле

Y-Axis

уберите флажок Auto

Grid,

в поле ввода Number of

Grids введите число 4.

Измененный график появится на экране (рис. 8.7).

8. Чтобы модернизировать график, выполните следующие шаги:

установите курсор на графике и двумя щелчками мыши вызовите

диалоговое

,01010

Formatting Currently Selected X-Y Plot;

в диалоговом окне выберите вкладку Traces (рис. 8.8);

в однострочном поле Color установите цвет grn (зеленый);

в однострочном поле Туре установите bar (прямоугольник);

нажмите клавишу <0К>. Новое представление графика изображено

на рис. 8.9.

9. Чтобы добавить новый график к существующему:

Рис.

8.9. График функции f(x)

— после

редактирования вида графика

283

.V.

-10 -6 -2 *

-lft

Рис.

8.10. График функции

f(x) =

—

и g(x)

установите курсор

на

рабочем поле

строке справа

от

функции

/W;

введите с клавиатуры: g(x):(\/x);

нажмите клавишу

<Enter>.

На экране появится: g(x):=—;

выделите график;

щелкните мышью на графике функции. Установите курсор справа

от /(*);

наберите на клавиатуре запятую. Курсор перейдет на следующую

строку;

наберите на клавиатуре g(x). Нажмите клавишу <Entef>;

измените цену деления на оси X, изменив строку х: = —10..10 на

х: = -10-9.5..10;

линию графика g(x) изобразите по своему усмотрению, используя

диалоговое окно Formatting Currently Selected X-Y Plot. На рис. 8.10

выбран точечный график (Type — points, Weight —3) голубого цвета

(blue).

Работа № 3. Решение нелинейных уравнений

Цель работы: поиск корня нелинейного уравнения с помощью

функции Root.

Задание: определить значение корня уравнения x+lg(x)+ln(x/10)

= 11.1 с точностью 10~

, если известно, что х е

[10; 11].

284

Методика выполнения работы

Многие уравнения не имеют аналитических решений. Они могут

решаться численными методами с заданной погрешностью. Для про-

стейших уравнений вида F(x)

0 решение находится с помощью функ-

ции root (Выражение, Имяпеременной). Функция root возвращает зна-

чение переменной, при котором выражение становится равным нулю,

т. е. F(x)

Для решения уравнения надо сначала задать начальное значение

переменной. Функция всегда имеет несколько решений, поэтому вы-

бор решения определяется начальным значением переменной.

Введем условные обозначения:

/(х) — функция, приравниваемая к 0;

TOL — точность вычисления;

х — начальное значение переменной;

х\

— приближенное решение функции f(x).

Выведите на экран панели инструментов, необходимые для ра-

боты:

для вывода панели 1 (рис. 8.3) выполните команду F10

—>

View

—>

Math Palette;

щелчком мыши на первой пиктограмме панели 1 выведите на эк-

ран панель 4 — Arithmetic Palette (Счет), предназначенную для набора

различных математических формул.

Задание вида функции и условий:

в рабочей области экрана с клавиатуры введите функцию

/(x):=x + lg(x) + ln(x/10)

-11.1;

в рабочей области экрана введите точность TOL: = 10

—3

и началь-

ное значение переменной х: = 10;

функции, которые не заданы в MathCad в явном виде, необходимо

выразить через другие функции, например lg(x) = ln(x)/ln(10).

Решение нелинейного уравнения с помощью функции root.

В рабочей области экрана наберите xl: = root(/Xx),x). Нажмите

<Enter>.

Вывод на экран значения xl:

наберите xl =

<Enter>.

На экране появится приближенное значение

xl.

По умолчанию количество знаков после запятой равно 3;

если требуемая точность превышает 10"

, необходимо изменить

формат вывода результата на экран командой

Fl O^Format-tNumber^Displayed Precision.

285

Задания для самостоятельной работы

Задание № 1

Решите соответствующую Вашему варианту систему линейных

уравнений:

12х]-20х

+5х

= 5

3xi + 2х

+ 5х

2xi -

8x2

+ 5хз = 5

12xi -2х

+ 1хз = 5

3xi + 2х

+ 2хз = 6

6xi - 2х

+ Зхз = 5

8xi - Зх

5.6хз

= 5

3xi - 2х

+ 2.5хз = 6

6х] -2х

+ 3.8хз = 5

20х!

2х

4хз

= 3

ЗОх, + 2х

+ 5х

= 4

2х]

—

6х

+ 5хз

7xj - Зх

1 .бхз

= 5

3xi - 20х

+ 2.5х

= 6

16xi -

2х

+ Зхз = 5

6. -8.5xi-7x

5.2хз

= 5

-9xi - 2х

5.5хз

= 6

-6xi + 7х

+ 2.8х

= 8

Задание № 2

Построить график функции:

Вариант

задания

Вид функции

№

2 +

х-х-

(/-*)<

>{l-xf>

-6х

+9х + 4

~7х

2х

-х'

Пределы

изменения

аргумента

0.1

0,2.. 1,5

0,1.

.0,6

0,2..1,5

2.4

-1 0,8

Шаг

изменения

аргумента

0.01

0.05

0.001

0.01

0.1

0.01

Задание № 3

Определить корень нелинейного уравнения:

х +0,323 - —=

с точностью е = 10

, если х

=0,8.

286

lg(jc) + VJc=l,56

с точностью Е = 10"", если х

=2.

х-е

4,28

с точностью е =

, если х

=1,2.

х+х

+ Vx

=4,75

с точностью

10~

если х

=1,5.

x-Vx =0,109

с точностью 8=10", если х

=1,1.

6. х

+х=3,3

с точностью е=10~

, если х

=1,4.

Глава 9

Векторный редактор

CorelDraw 9

CorelDraw — на сегодняшний день самый популярный графичес-

кий редактор, работающий с векторной графикой.

В настоящее время в эксплуатации находится версия 9.0 этой про-

граммы. Для учебно-методических целей эта версия представляет осо-

бый интерес, поскольку имеет русскоязычный аналог. На примере

этой популярной программы мы рассмотрим основные приемы созда-

ния и редактирования графических образов.

9.1.

Главное

окно,

элементы интерфейса

Интерфейс программы CorelDraw выполнен в традициях, ставших

стандартом для приложений в операционных системах Windows.

После того как графический редактор CorelDraw запущен, на экра-

не появится рабочее окно программы (рис. 9.1).

Основные элементы управления программы сосредоточены в стро-

ке меню, стандартной Панели инструментов, Панели свойств и Пане-

ли инструментов Графика. Основную же часть окна составляет рабо-

чая область, где в центре представлена рабочая страниц — это не

более чем ориентир, создавать объекты можно как на странице, так и

вне ее, но при выводе на печать будет напечатано только то, что нахо-

дится внутри рабочей страницы.

Заголовок, кнопки управления, строка меню, расположенные

в верхней части окна, а также полосы прокрутки и строка состояния

аналогичны таким же элементам любого приложения Windows.

В правой части окна расположена палитра цветов, с помощью ко-

торой вы можете задавать цвет элементам изображения. Сверху и сле-

288

--Г-;

Панель

•" i ' ^-jfflcrpyMeHTOB

*'•

(Графика)

' ' Строка __

! ' счхточтчп щ

Рис.

9.1. Основное окно программы CorelDraw

ва в окне расположены измерительные линейки, предназначенные для

точного позиционирования объектов и определения их размеров.

На стандартной панели инструментов содержатся инструменты,

которые можно встретить во многих других программах Windows:

{New {Создать), Open {Открыть), Save {Сохранить) и т. д.), а так-

же инструменты, которые присущи только приложениям CorelDraw:

Import {Импортировать), Export {Экспортировать), Application

Launcher {Кнопка запуска приложений), What's thisl {Справочная

система).

Панель свойств, расположенная по умолчанию непосредственно

под стандартной панелью инструментов, обладает уникальными ин-

терактивными свойствами. Состав ее элементов управления динами-

чески меняется в зависимости от типа выбранного объекта. Так, на-

пример, при выборе текста на Панели свойств появляются элементы

управления свойствами текста, при выборе линии — элементы

управления свойствами линии. Каждый тип объектов имеет на Па-

нели свойств присущий только ему комплект элементов управления.

Особенностью интерфейса CorelDraw является наличие таких эле-

ментов, как прикрепленные панели, которые обладают свойствами

289