Новиков А.И., Орлов Г.С. Линейная алгебра и аналитическая геометрия
Подождите немного. Документ загружается.

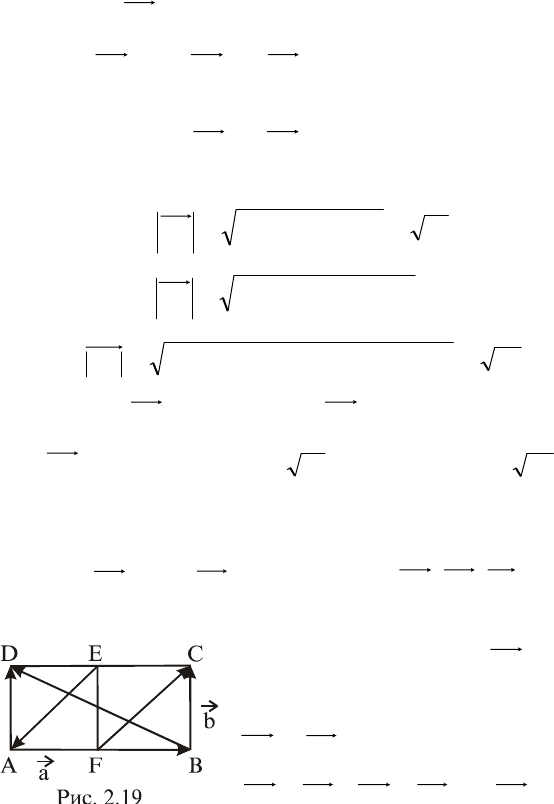
80
3;0;430;11;22AС
.
Далее
2;6;41;3;22AB2BA2BA2
.
Теперь найдем длины сторон треугольника. Поскольку ко-
ординаты векторов
AB
и
AC
известны, то длины сторон АВ,
АС и
BC
находим по формуле (2.10):
14132AB
22
2
;
5304AC
2
2
2
.
29402102BС
22
.
Ответ:
;1;3;2AB
;
2;6;4BA2
;
;;3;0;4AC
29BC;5AC;14AB
.
2.6.2. Решение типовых задач
Задача 2.1. В прямоугольнике
ABCD
(рис. 2.19) даны век-
торы
ABa
и
BCb
. Найти векторы
FC,EA,BD
, если
F
середина стороны
AB
, а
E
середина стороны
DC
.
Решение. Вектор
BD
можно
найти двумя способами. По правилу
параллелограмма как сумму векторов
BA
и
BC
:
abABBCBABCBD
.
81
С другой стороны, можно рассуждать так: вектор
BD
направ-
лен из конца вектора
AB
в конец вектора
BCADAD
и то-
гда по определению разности векторов
abABADBD
.
Аналогично
ba21BCA21EFEDEA
B
,
ba21BCA21BCFBFC
B
.
Ответ:
abBD
;
ba
2
1
EA
;
ba
2
1
FC
.
Задача 2.2. Вектор
1;2;3a
приложен в точке
4;2;1A
. Найти координаты точки
B
конца вектора
ABa
, а также орт
0
a
вектора
a
.
Решение. Пусть точка
B
имеет координаты
z;y;x
. В со-
ответствии с формулой (2.9) получаем
4z,2y,1x1,2,3
,
откуда, по определению равенства двух векторов, имеем
1x3
,
2y2
,
4z1
или
3z,4y,2x
.
Первая часть задачи решена. Найдем
0
a
.
Поскольку
222
123a
и
a
a
,
a
a
,
a
a
a
a
a
z
y
x
0
,
то
14
1
,
14
2
,
14
3
a
0
0
.
82
Ответ:
3;4;2B
,
14
1
,
14
2
,
14
3
a
0
.
Задача 2.3. Выяснить, можно ли из векторов
6;7c;0;2b;2;1a
выделить базис на плоскости.
Если такой базис существует, разложить третий вектор по бази-
су.
Решение. Как известно (п.2.4), всякие три вектора на плос-
кости линейно зависимы, т.е. заданные векторы
c,b,a
в сово-
купности линейно зависимы. Базис на плоскости образуют два
неколлинеарных вектора. Проверим, образуют ли базис векторы
a
и
b
. По определению линейной независимости векторов в
этом случае равенство
0ba
21
должно выполняться
только для нулевых
1
и
2
. Проверим, так ли это.
0,00,22,1
21
или
0,002,2
2121
,
откуда
.02
,02
1
21
Эта система имеет только нулевое решение:
0
1
,
0
2
. Значит, векторы
b,a
линейно независимы, т.е. образуют базис
на плоскости. Разложим теперь вектор
c
по базису
b,a
. Пусть
bac
, где
и
числа, подлежащие определению.
Перепишем линейную комбинацию
bac
в координат-
ной форме
0,22,16,7
или
2,26,7
,
83
откуда получаем систему
6.2
,72
Решая ее, находим
.2,3
Итак,
b2a3c
.
Ответ: базис
b,a
;
b2a3c
.
2.6.3. Задачи для самостоятельной работы
1. В треугольнике
ABC
даны векторы
aAB
,
bBC
,
cAC
. Выразить через
c,b,a
векторы, совпадающие с медиа-
нами
CL,BN,AM
треугольника.
2. В прямоугольнике
АВСD
даны векторы
aAC
,
bBD
, совпадающие с диагоналями параллелограмма. Выра-
зить через
a
и
b
векторы
AB
,
BC
,
CD
,
DA
, совпадающие
со сторонами прямоугольника.
3. Определить начало вектора
1;3;2a
, если его ко-
нец совпадает с точкой
2;1;1B
. Найти также модуль и орт
0
a
вектора
a
.
4. В пространстве в прямоугольной декартовой системе ко-
ординат даны точки
1;1;1A
,
0;2;3B
. Найти расстояние от
этих точек до начала координат и проекции вектора
AB
на ко-
ординатные оси.
5. Даны две координаты
4a
x
,
12a
y
вектора
a
.
Определить третью координату
z
a
при условии, что
13a
.
6. На плоскости даны два вектора
3;2p
и
4;9q
.
Проверить, образуют ли они базис и, если образуют, найти раз-
ложение вектора
14;49d
по базису
q,p
.
84
7. Проверить, образуют ли базис векторы
c,b,a
.
а)
3;1;2a
,
1;2;0b
,
0;4;6c
,
б)
1;0;1a
,
1;2;1b
,
3;2;1c
.
Если векторы
c,b,a
не образуют базис, то найти линейную за-
висимость между ними.
ОТВЕТЫ
1.
b
2
1
aAM
,
ac
2
1
BN
,
a
2
1
ca
2
1
bCL
.
2.
ba
2
1
AB
,
ba
2
1
BC
,
ab
2
1
CD
,
ba
2
1
DA
.
3.
3;2;1A
,
14a
,
1;3;2
14
1
a
0
.
4.
3A,O
,
13B,O
,
4ABПр
x0
,
1ABПр
y0
,
1ABПр
z0
.
5.
3
. 6.
q5p2d
.
7. а)
c,b,a
образуют базис;
б)
c,b,a
линейно зависимы:
0cba2
.
85
2.7. Скалярное произведение векторов
2.7.1. Определение и свойства
Определение. Скалярным произведением двух векторов
a
и
b
называется число (скаляр), равное произведению моду-
лей этих векторов на косинус угла между ними. Обозначается
скалярное произведение
b,a
или
ba
:
b,a
cosbab,a
. (2.14)
Скалярное произведение можно записать еще в одной форме
aПрbbПрab,a
ba
. (2.15)
Действительно,
bПрb,acosb
a
;
aПр
b,a
cosa
b
.
Из (2.15) следуют формулы для вычисления алгебраических
проекций векторов
a
b,a
bПр
a
;
b
b,a
aПр
b
. (2.16)
Скалярное произведение обладает следующими свойствами.
Алгебраические свойства
1.
a,bb,a
.
2.
b,ab,a
,
- действительное число.
3.
c,ab,acb,a
.
4.
2
aa,a
.
86
Замечание. Скалярное произведение
a,a
называется
скалярным квадратом вектора
a
и обозначается
2
a
, т.е.
2
2
aaa,a
.
Геометрические свойства
5. Если векторы
a
и
b
перпендикулярны, то
0b,a
.
Действительно,
00ba2cosbab,a
.
Скалярное произведение равно нулю и для нулевых векторов,
т.е. если
0a
или
0b
.
6. Если векторы
a
и
b
ненулевые, то
0b,a
, если
2
b,a
0
,
0b,a
, если
b,a
2
.
Алгебраические свойства используются при нахождении
скалярного произведения двух линейных комбинаций несколь-
ких векторов.
Пример 2.6. Вычислить
b4a,ba2
, если
ba
и
2a
,
3b
.
Решение. Используя распределительное свойство 3, полу-
чаем
b4,bb4,a2a,ba,a2b4a,ba2
87
22
22
b4b,a7a21свойствупо
b4b,a8a,ba22свойствупо
4свойствупоbaкактак,0b,a
289442b4a2
22
.
Ответ:
28
.
2.7.2. Скалярное произведение в координатной форме
Утверждение. Если векторы
a
и
b
заданы своими ко-
ординатами:
zyx
a,a,aa
;
zyx
b,b,bb
в ортонормированном базисе
k,j,i
, то скалярное произ-
ведение
b,a
определяется формулой
zzyyxx
bababab,a
. (2.17)
Доказательство. Предварительно заметим, что
1ii,i
2
. Аналогично
1k,kj,j
. Для других комби-
наций векторов
k,j,i
с учетом их взаимной перпендикулярно-
сти имеем
0k,jk,ij,i
,
используя эти результаты и алгебраические свойства 1-3, полу-
чаем
yxxxzyxzyx
bai,ibakbjbib,kajaiab,a
j,jbai,jbak,ibaj,i
yyxyzx
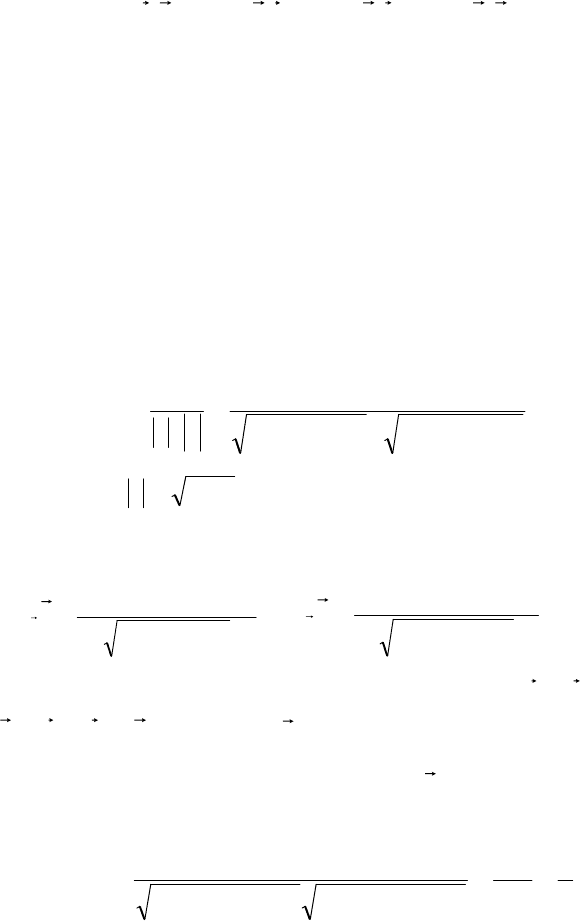
88
k,kbaj,kbai,kbak,jba
zzyzzzzy
0ba1ba0ba0ba0ba1ba
zyyyxyzxyxxx
zzyyxxzzyzxz
bababa1ba0ba0ba
. ■
Замечания. 1. Формула (2.17) позволяет записать в коор-
динатной форме условие перпендикулярности двух векторов
0b,a
:
0babababa
zzyyxx
.
2. Из (2.14) с учетом (2.17) следует формула для нахожде-
ния угла между двумя векторами, заданными своими координа-
тами в ортонормированном базисе
2
z
2
y
2
x
2
z
2
y
2
x
zzyyxx
bbb:aaa
bababa
ba
b,a
b,aсos
. (2.18)
Заметим, что
a,aa
.
3. В ортонормированном базисе формулы (2.16) для алгеб-
раических проекций векторов переписываются в виде
,
aaa
bababa
bПр
2
z
2
y
2
x
zzyyxx
a
2
z
2
y
2
x
zzyyxx
b
bbb
bababa
bПр
.(2.19)
Пример 2.7. Найти угол между векторами
j4i3a
и
k3j2i6b
, а также
bПр
a
.
Решение. Поскольку
0;4;3a
;
3;2;6b
, то в
соответствии с формулой (2.17) имеем
7
2
75
10
326043
302463
b,a
сos
2
222
2
2
;
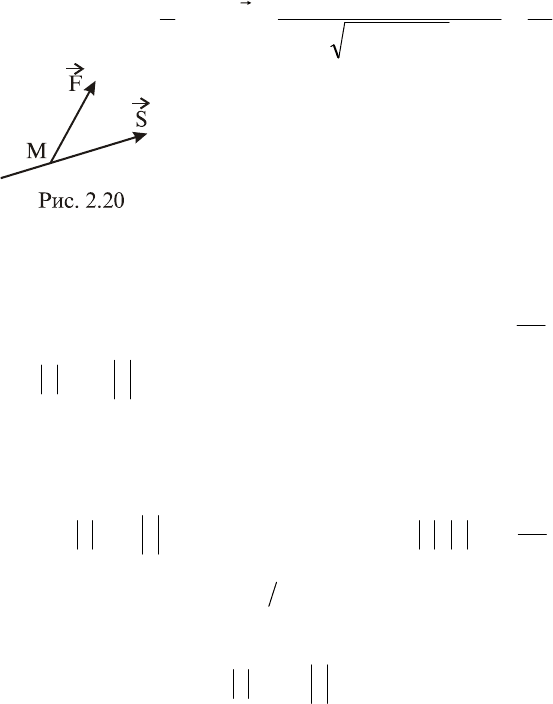
89
2
5
10
43
302463
bПр,
7
2
arccos
b,a
2
2
a
.
В механике скалярное произведение находит
применение при вычислении работы
A
силы
F
при перемещении материальной точки
M
из начала вектора перемещения
S
в его конец
(рис. 2.20):
S,FA
.
2.7.3. Решение типовых задач
Задача 2.4. Векторы
a
и
b
образуют угол
3
2
. Зная,
что
3a
,
4b
, вычислить
b2a,b2a3
.
Решение
b;b4a;b2b;a6a;a3b2a,b2a3
3
2
cosba416493b;a4b4a3
2
2
61214346427
.
Ответ: -61.
Задача 2.5. Дано:
3a
,
5b
. Определить, при каком
значении
векторы
ba
,
ba
будут перпендикулярны.
Решение. Предположим, что
baba
, тогда
0b,ba,bb,aa,a0ba,ba
2
