Никифоров В.О. и др. Интеллектуальное управление в условиях неопределенности
Подождите немного. Документ загружается.

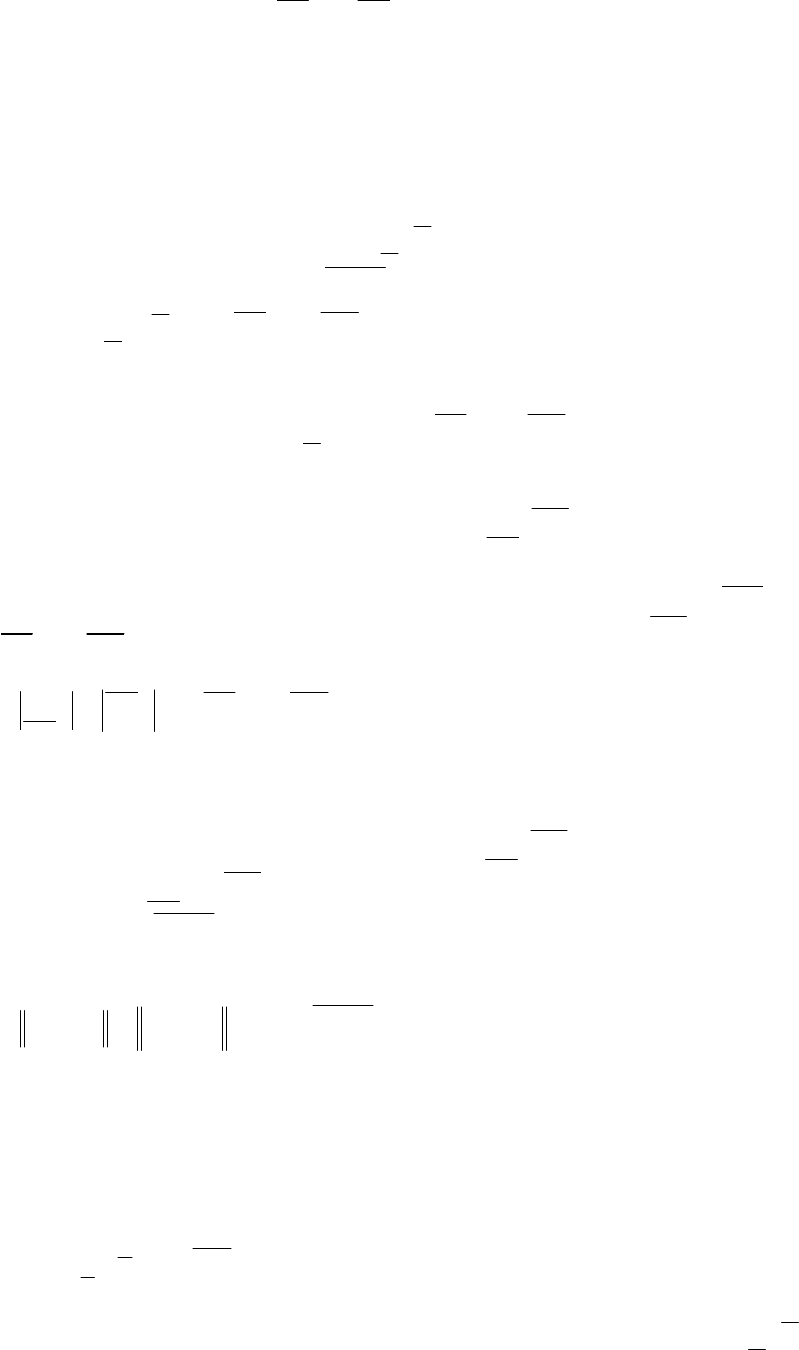
215
[][ ]
klniBAC
m
j
jlijil
,1 ;,1 ;][
1
==⋅=
∑
=
, (П.5.31)
где произведение
[
]
[
]
jlij
BA ⋅ интервальных чисел определяется в
соответствии с (П.5.9)–(П.5.11), а суммирование этих произведений
осуществляется в соответствии с (П.5.12), (П.5.13).
Определение П.5.15. Угловой реализацией
(
)
ν
c
A )( mn × -
интервальной матрицы
][] ,[][
0
AAAAA
Δ
+
=
=
, получаемой в
результате
ν
-й выборки
nm
2 ,1=
ν
из множества мощности, равной
)(nm пар
{
}
mjniAA
ij
ij
,1 ;,1 , , == граничных значений интервальных
скалярных компонентов ][
ij
A матрицы
][
A
, называется матрица
()
(
)
{
}
(
)
{
}
mjniAAAcolrowA
ij
ij
cijc
,1 ;,1 ; , ==∈=
ν
ν
(П.5.32)
с фиксированными на этой реализации компонентами. □
Утверждение П.5.5. Пусть ]A ,[][ ΔΔ=Δ AA – интервальный
матричный компонент матрицы ][
A
в силу факторизации в форме
(П.5.29), тогда интервальные компоненты
[][, A],
ij
ij
ij
AAΔ=Δ Δ
1, ; 1,injm==, обладают тем свойством, что
mjniAA
ij
ij
,1 ;,1 , ==Δ=Δ , (П.5.33)
которое выполняется в силу (П.5.27), (П.5.28).
Утверждение П.5.6. Угловые реализации
(
)
ν
c
A
Δ
и
()
μ
c
AΔ
)( mn
× -интервальной матрицы ]A ,[][ ΔΔ=Δ AA с граничными
компонентами
A
Δ
и A Δ (П.5.28), полученные в результате
ν
-й и μ-й
выборок
mn
2 ,1 , =
μ
ν
в силу (П.5.32) и свойства (П.5.33), обладают
равными матричными нормами так, что выполняется равенство
()
(
)
mn
cc
AA 2 ,1 , ; =Δ=Δ
μν
μυ
(П.5.34)
Определение П.5.16. Интервальным полиномом
[
]
)(zD степени
n называется полином, коэффициенты которого являются
интервальными числами так, что он принимает вид
[][][]
[
]
[
]
[
]
nn
nnn
azazazazazD +++++=
−
−−
1
2
2
1
10
)( Κ (П.5.35)
где
[][]
niaaa
i
i
i
,0 ; , == . □
Определение П.5.17. Интервальным характеристическим
полином (ИХП)
[]
)(
λ
D интервальной )( nn
×
-матрицы ] ,[][ AAA =
называется интервальный полином степени
n , получаемый в силу

216
определения характеристического полинома произвольной )(
nn× -
квадратной матрицы
()
][][][][][][det
1
2
2
1
10 nn
nnn
aaaaaA +λ++λ+λ+λ=−Ιλ
−
−−
Κ
(П.5.36)
так, что
(
)
][det)]([ AD −Ιλ=λ
. □
Приведем несколько способов вычисления коэффициентов ИХП
интервальной )(
nn× -матрицы
][
A
.
Способ 1. Способ основан на обобщенной теореме Ф. Виета.
Пусть спектр собственных значений интервальной матрицы ][
A
{
}
(
)
{
}
[] [ ] , : det [] 0; 1,
i
ii
A
Ain
⎡⎤
σ=λ=λλ λΙ−==
⎣⎦
(П.5.37)
известен, тогда ИХП (П.5.36) представим в форме
[]
()
1
01 1
1
() [ ] [ ] [ ] [ ] [ ]
n
nn
nn i
i
Daa a a
−
−
=
λ= λ+ λ + + λ+ = λ−λ
∏
K, (П.5.38)
где 1]1 ,1[][
0
==a .
Обощенная теорема Виета устанавливает связь собственных
значений
][
i
λ
с коэффициентами nia
i
,1 ];[ = в форме
1
1
[] [];
n
i
i
atRA
=
=− λ =−
∑
(П.5.39)
212
11
22
12
[] [ ][ ];
n
ii
i
i
ii
a
=
=
<
=λ⋅λ
∑
(П.5.40)
3123
11
22
33
123
[] [ ][ ][ ];
n
ii i
i
i
i
ii i
a
=
=
=
<<
=− λ ⋅λ ⋅ λ
∑
(П.5.41)
Μ
1
1121
11
22
(1) 1
12 ( 1)
[](1) [][][ ];
n
n
niiim
i
i
in n
ii im
a
−
−−
=
=
−=−
<<< −
=− λ ⋅λ λ
∑
M
K
K
(П.5.42)
1
[](1) [].
n
n
ni
i
a
=
=− λ
∏
□ (П.5.43)
Способ 2. Способ Г. Крамера главных миноров.
1
11
[] [] , ;
nn
ii
ii
ii
atRA A A
==
⎡⎤
=− =−
⎢⎥
⎣⎦
∑∑
(П.5.44)
217
1
[](1) [ ],
k
k
kii
i
aM
=
=−
∑
(П.5.45)
где ][
ii
M – алгебраическое дополнение )(ii -го элемента ][
ii
A матрицы
][
A
;
[](1)det[].
n
n
aA=− □ (П.5.46)
Способ 3. Способ У.Ж.Ж. Леверье.
∑
=
+−
−
=−=
k
i
ik
ik
nkAtra
k
a
1
1
1
;,1 ];[][
1
][ (П.5.47)
.1][
0
=a □
Способ 4. Способ Д.К. Фаддеева:
{}
,,1 ;]][[
1
][
1
nkHAtr
k
a
kk
=−=
−
(П.5.48)
где
.][ ;][]][[][
01
Ι
=
Ι+=
−
HaHAH
kkk
□ (П.5.49)
218
ПРИЛОЖЕНИЕ 6
Свойство строгой положительной вещественности
Рассмотрим передаточную функцию вида
0
1
1
1
1
)(
apap
bpbpb
sH
n
n
n
o
m
m
m
m
+++
+++
=
−
−
−
−
Λ
Λ
. (П6.1)
Критерий строгой положительной вещественности: передаточная
функция
)(
s
H
является строго положительно вещественной (СПВ-
функцией) только в том случае, если
(У1) она не имеет полюсов в области
0]Re[ ≥
s
;
(У2)
0)](Re[ >
ω
j
H
для всех
−
∞<ω<∞;
(У3)
2
lim Re[ ( )] 0Hjωω> при
ω
→∞.
Для пояснения приведенного критерия рассмотрим передаточную
функцию апериодического звена первого порядка
1
)(
+
=
Ts
k
sH
A
, (П6.2)
где 0>k – коэффициент усиления, а 0>
T
– постоянная времени.
Покажем, что передаточная функция (П6.2) удовлетворяет условиям
(У1)–(У2). Действительно, единственный полюс функции (П6.2)
T
s
/
1−= лежит вне области 0]Re[ >
s
. Как известно, частотный
годограф апериодического звена первого порядка полностью лежит в
четвертом квадранте комплексной плоскости, что гарантирует
выполнение условия (У2) (см. рис. П6.1). Наконец, рассмотрим
частотную передаточную функцию звена:
22 22
()
11 1
A
kkkT
Hj j
jT T T
ω
ω= = −
ω+ ω + ω +
.
Тогда
2
22 2
lim 0
1
kk
TT
⎛⎞
ω=>
⎜⎟
ω+
⎝⎠
ω→∞
,
что означает выполнение условия (У3).
Таким образом, можно сделать вывод, что СПВ-функции
обладают почти такими же частотными свойствами, что и звено
первого порядка. Так, их частотные годографы лежат в правой
полуплоскости (следовательно, фазовый сдвиг, вносимый
динамическим звеном с такой передаточной функцией, не превышает
0
90 ). Кроме того, скорость убывания вещественной части частотной
передаточной функции при
ω
→∞ не быстрее, чем у
2
1/ω . Из
219
сделанного вывода видно, что класс строго положительно
вещественных передаточных функций является достаточно узким, и
далеко не все линейные модели реальных объектов будут
удовлетворять условиям (У1)–(У2).
Отметим следующие свойства строго положительно
вещественных передаточных функций:
1) если )(
/
)()(
s
B
s
A
s
H
= является СПВ-функцией, то оба
многочлена )(
s
A
и )(
s
B
гурвицевы, а их степени отличаются не
больше, чем на единицу;
2) если )(
s
H
является СПВ-функцией, то )(
/
1
s
H
– также СПВ-
функция;
3) если )(
1
sH и )(
2
sH – СПВ-функции, то
12
() ()
H
sHs
α
+β –
также СПВ-функция для любых положительных
α
и
β
;
4) если
)(
1
sH и )(
2
sH являются передаточными функциями
прямой и отрицательной обратной связи, то передаточная функция
замкнутой системы ))()(1/()()(
211
sHsHsHsH
+
=
также является
СПВ-функцией.
220
ПРИЛОЖЕНИЕ 7
Свойства многомерных адаптивных систем управления
Для исследования свойств адаптивной системы, состоящей из
объекта (4.50), (4.51), эталонной модели (4.53), (4.54), настраиваемого
регулятора (4.59) и алгоритма адаптации (4.61), используем функцию
Ляпунова
1
(, )
22
TT
Veq ePe qq
β
=+
γ
%%
%
. (П7.1)
Неизвестный положительный параметр
β
может быть включен в
выражение для функции Ляпунова, так как в теоремах об
устойчивости используется только факт существование функции
Ляпунова, но не требуется точного вычисления ее значений.
Производная функции (П7.1) в силу уравнений модели ошибки
T
M
eAe hq=+βω
&
%
, (П7.2)
T
qhPe=−γω
&
%
(П7.3)
имеет вид
11
22
TT T
VePeePeqq
β
=++=
γ
&
&
&&%%
() 0
TT TT TT T
MM
eAPPAe q hPe q hPe eQe=− + +β ω −β ω =− ≤
%%
.
Последнее неравенство означает устойчивость по Ляпунову
нулевого состояния равновесия модели ошибки (П7.2), (П7.3)
(теорема П2.1 из приложения 2) и справедливость предела (4.63)
(теорема П2.4 из приложения 2).
Для исследования свойств нелинейной робастной системы,
состоящей из объекта (4.50), (4.51), эталонной модели (4.53), (4.54) и
нелинейного регулятора (4.72), используем функцию Ляпунова
PeeeV
T
2
1
)( =
. (П7.4)
Подставляя управление (4.72) в уравнение (4.57) и добаляя
внешнее возмущение
δ, получаем модель ошибки замкнутой системы
нелинейного робастного управления
2
(|| )
TT
M
eAe h q hPe=+βω−γω +δ
&
. (П7.5)
Вычисляя производную функции (П7.4) в силу уравнения (П7.5),
получаем
22
||| |
TTT TT
V e Qe q h Pe h Pe e Ph=− +β ω −γ ω + δ
&
.

221
Переходя к нормам и выделяя в правой части неравенства полный
квадрат разности, получим:
222
|| ||||| | ||| | ||| |
TT
Q
V e q h Pe h Pe e Ph≤−λ +β ω −γ ω + δ=
&
222 2 2
1
|| ||| | ||||| | || ||
244
TT
Q
ehPeqhPeqq
⎛⎞
ββ
=− λ − γ ω −β ω + + −
⎜⎟
γγ
⎝⎠
22222
111
|||||| || ||
222
Q
QQ
e e Ph Ph Ph
⎛⎞
−λ−δ+δ+δ
⎜⎟
⎜⎟
λλ
⎝⎠
=
2
2
2
111
|| | || | | | || | |
222
2
Q
T
Q
Q
ehPeqePh
⎛⎞
⎛⎞
λ
β
⎜⎟
=− λ − γ ω − − − δ +
⎜⎟
⎜⎟
γ
λ
⎝⎠
⎝⎠
222
1
|| | |
42
Q
qPh
β
++ δ
γλ
,
где
Q
λ – минимальное собственное значение матрицы Q , а δ –
верхняя оценка ограниченного возмущения
δ
(т.е. |()|t
δ
≤δ для всех
0
≥
t
). Усиливая неравенство, пренебрежем квадратными членами.
Окончательно получим
22 22
11
|| || | |
242
Q
Q
VeqPh
β
≤− λ + + δ
γλ
&
(П7.6)
или
222
1
|| | |
42
Q
PQ
VVq Ph
λ
β
≤− + + δ
λγ λ
&
(П7.7)
(переход от выражения (П7.6) к формуле (П7.7) осуществлен с
использованием неравенства Релея). Из (П7.6) видно, что при
нарушении неравенства (4.73) производная функции Ляпунова
становится отрицательной. Это доказывает сходимость ошибки
слежения к предельному установившемуся множеству (4.73).
Проинтегрировав неравенство (П7.7), получим, что скорость
сходимости к предельному множеству является экспоненциальной
(решение аналогичной задачи приведено в
п. 5.1.4). Наконец, обнулив
в выражении (4.73) величину
δ
, убеждаемся, что предельное значение
установившейся ошибки может быть сделано произвольно малым за
счет увеличения коэффициента нелинейной обратной связи
γ
.

222
ПРИЛОЖЕНИЕ 8.
Расчетное задание по курсу «Интеллектуальное управление в
условиях неопределенности»
Для непрерывного объекта управления, заданного в виде
передаточной функции (ПФ) «вход-выход (ВВ)» НОУ
))1()1()1())(1()1((
)1()1(
),(
7463
2
524130
2110
qasqasqaqasqa
qbsqb
qs
++++++++
+
+
+
=Φ
,
где 0
70605040302010
=
=
=
==== qqqqqqq – номинальные значения
параметров
0j
q , 7,1=j :
1.
Построить МТЧ непрерывного ОУ
),()(),()(),();()(),()(),( q
t
uqDq
t
x
q
C
q
t
y
t
uqBq
t
x
q
A
q
t
x
+
=
+=
&
в требуемом базисе; произвести ранжирование параметров
j
q
по потенциальной чувствительности к ним выхода ОУ с
использованием матрицы управляемости агрегированной
системы.
2.
Перейти к дискретному описанию ОУ
);()(),()(),1( kuqBqkxqAqkx +=+ )()(),()(),( kuqDqkxqCqky +
=
указанным в задании методом. Построить МТЧ
дискретного
ОУ
к вариации интервала дискретности.
3.
Синтезировать закон управления (ЗУ) вида u(t)=k
g
g(t)-kx(t),
который должен обеспечивать
системе
),()(),()(),();()(),()(),( q
t
uqDq
t
x
q
C
q
t
y
t
gqGq
t
x
q
F
q
t
x
+
=
+=
&
g
KqBqGKqBqAqF )()(,)()()(
=
−= ,
образованной объединением НОУ и ЗУ равенство входа
g(t) и
выхода
y(t) в неподвижном состоянии при номинальных
значениях параметров с помощью:
- матрицы
k
g
прямой связи по входу g(t);
- матрицы
k обратной связи по состоянию x(t)
распределение мод Баттерворта с характеристической частотой
0
ω .
Построить МТЧ спроектированной системы по каждому из
параметров и для значения
3.0=Δ
j
q ; выделить доминирующие
параметры по степени их влияния на величину
σ
перерегулирования и длительность t
п
переходного процесса;
223
4.
Построить матрицу функций модальной чувствительности и
выделить неблагоприятное сочетание вариаций параметров;
5.
Получить ВМО НОУ с интервальными параметрами
[] []
)()()();()()( tDutCxtytuBtxAtx
+
=
+=
&
,
[]
[
][]
[
]
,,
00
BBBAAA
Δ
+
=Δ+=
c использованием
интервальной арифметики на основе
интервальной реализации параметров q
j
, записываемых в форме
[]
[
]
jjj
qqq ,= при заданных граничных (угловых) значениях.
6.
Синтезировать закон медианного модального управления,
базовый алгоритм которого дополняется контролем нормы
0
F
медианной составляющей интервальной матрицы
[]
F
спроектированной системы с последующим вычислением
оценки F
I
δ , вычислить матрицы k
g
и k.
Закон управления (ЗУ) вида
u(t)=k
g
g(t)-kx(t) должен доставлять
системе
[] []
)()()();()()( tDutCxtytgGtxFtx
+
=
+=
&
[] []
[
]
[
]
[
]
[
]
[
]
,,
00
GGKBGFFKBAF
g
Δ
+
=
=
Δ
+=−=
образованной объединением НОУ и ЗУ равенство входа
g(t) и
выхода
y(t) в неподвижном состоянии при номинальных
значениях параметров с помощью:
-матрицы
k
g
прямой связи по входу g(t);
- матрицы
k обратной связи по состоянию x(t)
распределение мод Баттерворта с характеристической частотой
0
ω
, которая гарантирует достижение значение оценки
относительной интервальности матрицы состояния системы
0
F
F
F
I
Δ
=δ
не больше заданной
F
IR
δ
. Исследовать свойство
робастности ЗС, полученной в п.6, с помощью метода В.Л.
Харитонова.
ПРИМЕЧАНИЕ. При формировании интервального ВМО ВСВ
НОУ следует стремиться к тому, чтобы интервальной была бы
только матрица состояния НОУ.
7.
Оценить алгебраическую реализуемость неадаптивного или
адаптивного управления, обеспечивающего параметрическую
инвариантность выхода системы, и синтезировать его (по
выбору). Величина параметрической неопределенности ОУ
характеризуется величиной, указанной в табл. П8.1.
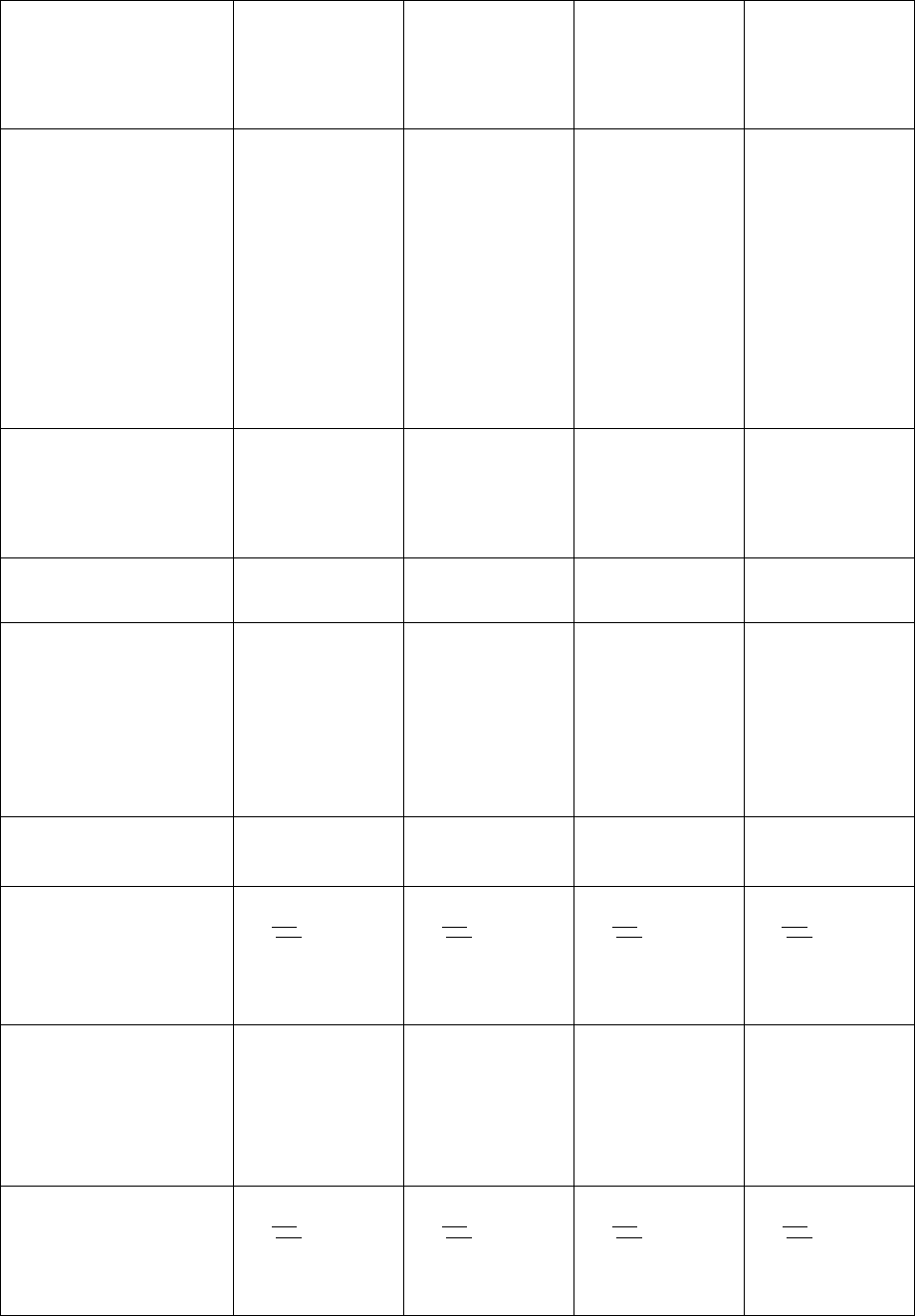
224
Таблица П.8.1
Варианты
Исходные
данные
A Б В
Г
1.1. Значения
параметров ПФ
3
0
=b ;
4.0
1
=b
;
2
0
=a ;
6.0
1
=a
;
0
2
=a ;
6
3
=a ;
10
4
=a
0
0
=
b ;
67.0
1
=
b
;
0
0
=
a ;
1
1
=
a
;
16
2
=
a ;
3
3
=
a ;
10
4
=
a
0
0
=
b ;
2
1
=
b
;
5
0
=
a ;
1
1
=
a
;
0
2
=
a ;
5.2
3
=
a ;
25
4
=
a
1
0
=b ;
25.0
1
=b
;
0
0
=a ;
1
1
=a
;
4
2
=a ;
3
3
=a ;
1
4
=a
1.2. Базис
описания НОУ
каноничес-
кий
управляе-
мый
каноничес-
кий
наблюдае-
мый
физический произволь-
ный
2.1. Интервал
дискретности
Δt=0.05с Δt=0.03с Δt=0.02c Δt=0.07с
2.2. Метод
перехода к ДОУ
заменой
производ-
ной
отношением
конечных
малых
с помощью
интеграль-
ной модели
ВСВ НОУ
заменой
производ-
ной
отношением
конечных
малых
произволь-
ный
3. Характеристи-
ческая частота
1
0
3
−
=ω c
1
0
5
−
=ω c
1
0
10
−
=ω c
1
0
15
−
=ω c
5. Граничные
(угловые)
значения
параметра
j
q
j
q = -0.2
j
q = 0.2
j
q = -0.3
j
q = 0.3
j
q = -0.4
j
q = 0.4
j
q = -0.5
j
q = 0.5
6. Относительная
интервальность
матрицы
состояния
системы
02.0
=
δ F
IR
03.0
=
δ
F
IR
04.0=
δ
F
IR
05.0
=
δ F
IR
7. Величина
параметрической
неопределеннос-
ти
j
q
= -0.2
j
q = 0.2
j
q
= -0.3
j
q = 0.3
j
q
= -0.4
j
q = 0.4
j
q
= -0.5
j
q = 0.5
