Никифоров В.О. и др. Интеллектуальное управление в условиях неопределенности
Подождите немного. Документ загружается.

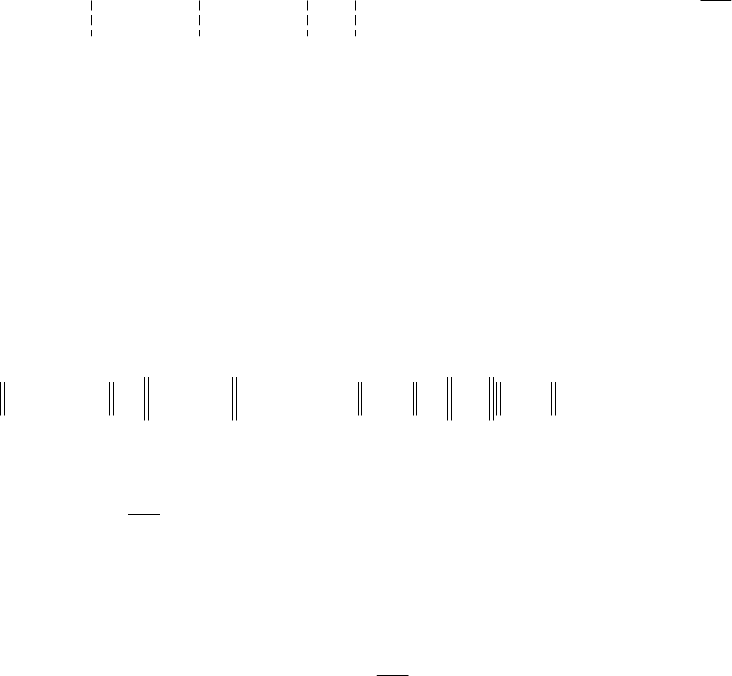
205
резольвента
1
)(
−
− AsI . Таким образом, в силу (П4.56), а также
условий утверждения 2.15 становится справедливой запись
jjj
DsDAsI
11
)()(
−−
λ−=− . (П.4.57)
Подстановка (П.4.57) в (2.191) приводит к цепочке соотношений:
00)()()()()(
1111
=⋅λ−=λ−=λ−=−=Φ
−−−−
ξχ jj
l
jjj
l
j
l
jl
sDCsDsCDAsICs
■ (П.4.58)
Доказательство утверждения 2.16. Пусть
l
C – левый
собственный вектор матрицы
A
, соответствующий ее собственному
значению
l
λ , тогда выполняется система равенств:
l
l
l
CAC λ= , (П.4.59)
l
l
l
l
ll
CACAACAC
22
λ=λ==
, (П.4.60)
Μ
ln
l
nl
l
nlnl
CACAACAC
1221 −−−−
λ==λ==Κ
. (П.4.61)
Если теперь с использованием (П.4.59) – (П.4.61), а также (2.190)
сформировать матрицу управляемости "вход-выход"
lj
W
χ
(2.185), то
получим
[
]
{
}
.,1;0)(
12
niWrowDCDCDCDCW
iljj
ln
lj
l
lj
l
lj
l
lj
===λλλ=
χ
−
χ
Κ
■ (П.4.62)
Доказательство утверждения 2.1.4. Свободное движение
))0()0 ),0( ,()(
x
x
(t,g(t)
x
t
x
t
x
=≡= системы (2.137) задается выражением
)0())0( ,( xextx
Ft
=
. (П.4.63)
Если в (П.4.63) осуществить переход к евклидовым векторным
нормам и согласованным с ними матричным нормам, то на основании
свойств SVD-разложения матричной экспоненты получим цепочку
равенств и неравенств
{
}
)0()0()0())0( ,( xexexextx
FtFt
M
Ft
=α== . (П.4.64)
Воспользуемся свойством матричной функции от матрицы
)(F
f
сохранять отношение матричного подобия
FM
M
=
Λ
, где
{
}
nidiag
i
,1 ; =λ=Λ , записываемого в одной из форм
1
)()( ,)()(
−
Λ==Λ MMfFfMFfMf . (П.4.65)
Тогда в силу (П.4.64) оказывается справедливым равенство
{
}
11
,1 ;
−
λ
−Λ
=== MnieMdiagMMee
t
tFt
i
. (П.4.66)
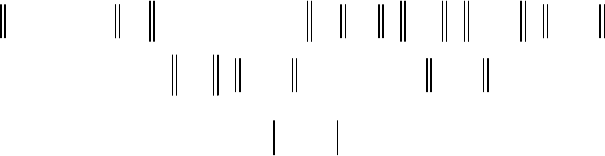
206
Подстановка (П.4.66) в (П.4.64) для ))0(,(
x
t
x
дает
{}
11
( , (0)) (0) (0)
(0) (0) ,
M
tt
t
t
M
xt x Me M x M e M x
CM e x e x
Λ− Λ −
−λ
Λ
=
≤⋅⋅ ⋅ =
=⋅=β⋅
(П.4.67)
где
{
}
{
}
; min Re .
MMi
i
CMβ= λ= λ
Доказательство утверждения 3.1. Зададим модальную модель с
матрицами
()
H ,Γ в форме автономной системы
),()();0();()(
t
Hz
t
z
t
z
t
z
=
η
Γ=
&
(П.4.68)
а непрерывный ОУ с тройкой матриц ),,(
C
B
A
– в форме (2.39)
)()( );0( );()()(
t
C
x
t
y
x
t
B
u
t
Ax
t
x
=
+
=
&
. (П.4.69)
Потребуем, чтобы управление )(
t
u обеспечивало при выполнении
условия )0()0(
Mz
x
= подобие процессов по вектору )(
t
x
состояния
ОУ процессам по вектору )(
t
z состояния ММ, записываемое в форме
t
t
Mz
t
x
∀= ),()(, (П.4.70)
где )( nn
M
×− – неособая матрица подобия так, что существует
1−
M
.
Дифференцирование (П.4.70) по
t
дает равенство
)()(
t
z
M
t
x
&
&
= . (П.4.71)
Подстановка в (П.4.71) выражений (П.4.68) и (П.4.69) приводит с
использованием (П.4.70) к выражению
()
),()( tzAMMtBu −
Γ
= (П.4.72)
которое может быть разрешено относительно управления )(
t
u в
функции )(
t
z состояния ММ:
()
)()()(
1
tzAMMBBBtu
TT
−Γ=
−
. (П.4.73)
Таким образом, (П.4.73) является решением задачи модального
управления, обеспечивающего выполнение векторного подобия
(П.4.70) в форме прямого программного управления программным
задатчиком желаемых траекторий в ОУ (П.4.69), порождаемых
множеством начальных состояний )0(
x
. Программным задатчиком
является ММ (П.4.68) с начальным состоянием
1
(0) (0)zMx
−
= с
прямой связью по вектору состояния )(
t
z с матрицей связей
)()(
1
AMMBBBK
TT
z
−Γ=
−
. (П.4.74)

207
Если пара матриц
()
H ,Γ полностью наблюдаема, то прямая связь
по вектору )(
t
z состояния ММ может быть заменена на прямую связь
по вектору )(
t
η выхода ММ, для чего на матрицу
M
подобия
необходимо наложить ограничение в форме матричного соотношения,
являющегося уравнением Сильвестра
BH
A
M
M
−
=−Γ . (П.4.75)
Подстановка (П.4.75) в закон (П.4.72) дает его реализацию в
форме
)()()()(
1
tHztBHzBBBtu
TT
−=−=
−
. (П.4.76)
Подставим теперь задачу поиска модального управления в форме
отрицательной обратной связи по вектору состояния )(
t
x
ОУ (2.3а),
(П.4.69) с матрицей связей
K
так, что она записывается в форме
() ().ut Kxt=− (П.4.77)
Нетрудно видеть, что, если в (П.4.76) подставить (П.4.70), то
получим матричное соотношение
,
K
M
H
= (П.4.78)
из которого следует (3.1). Подставим (П.4.78) в уравнение Сильвестра
(3.2), (П.4.75), тогда с учетом (3.3) получаем матричное условие
подобия матриц Γ и
F
в форме (3.4).
Теперь докажем корректность требования непересекаемости
алгебраических векторов
{
}
{
}
0
=
Γ
σ
σ
Ι
A собственных значений
матрицы
A
и
Γ
. Для этих целей предположим, что матрица
Γ
задана
в диагональной форме:
{
}
nidiag
i
,1 ; =λ=Λ=Γ , (П.4.79)
так что матричное уравнение Сильвестра (3.2), (П.4.75) примет вид
BH
A
M
M
−
=
−Λ
. (П.4.80)
Решим это уравнение, для чего запишем его в столбцовой форме:
.,1 ; niBHAMM
iii
=−=−Λ (П.4.81)
Для случая матрицы
Λ
=
Γ простой структуры столбец
i
Λ
имеет
вид
[]
,0 |0
1
T
T
ini
T
ii −−
λ=Λ
(П.4.82)
подстановка которого в (П.6.81) дает представление последнего в
форме
,)(
iii
BHMA −=−Ιλ (П.4.83)
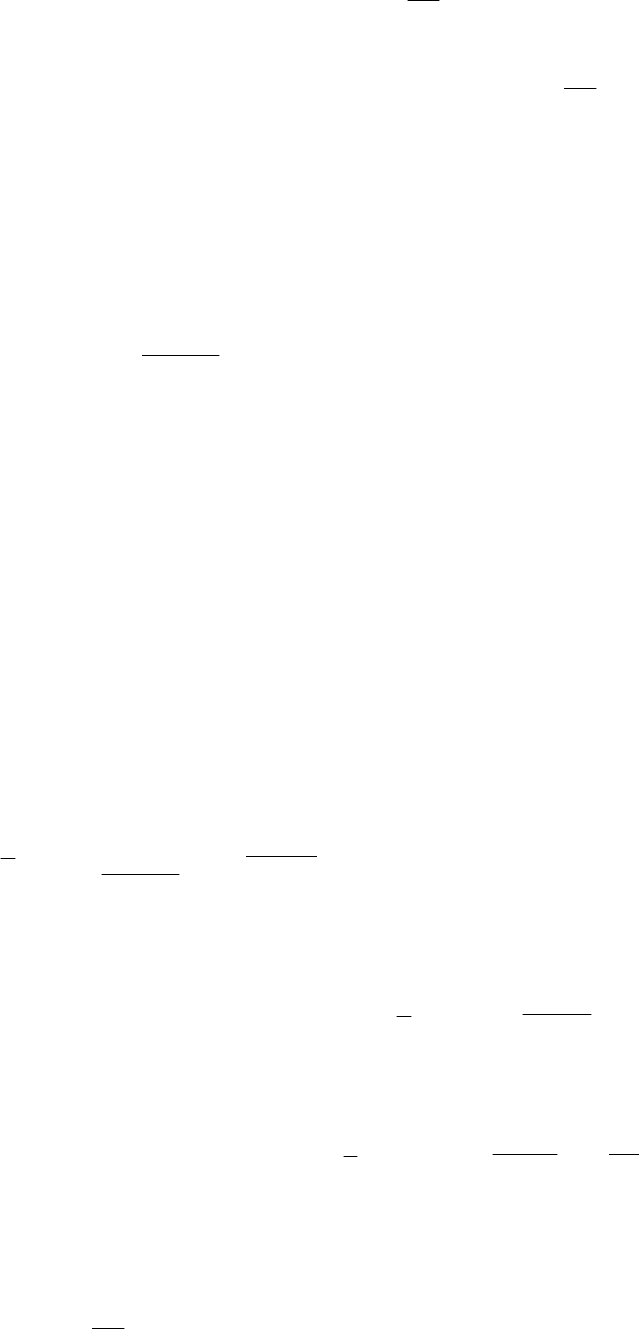
208
откуда для матрицы
M
получим
()
{
}
niBHAMrowM
iii
,1 ;
1
=−Ιλ−==
−
. (П.4.84)
Таким образом, только в случае выполнения условия
{} {}
0=σΓσ AΙ матричные блоки niA
i
,1 );( =−Ιλ оказываются
обратимыми, а, следовательно, существует решение матричного
уравнения Сильвестра (3.2), (П.4.75).
И, наконец, покажем справделивость требования управляемости
пары ) ,(
B
A
. Для этих целей воспользуемся разложением Фаддеева–
Леверье матрицы
1
)(
−
−Ιλ A
i
в (П.4.84), которое имеет вид
()
[]
,)()()()(
)(
1
1
0
2
321
1
−
−−−
−
λ++λ+λ+Ιλ×
×
λ
=−Ιλ
n
iininin
in
i
AdAdAdd
d
A
Κ
(П.4.85)
где
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
=λ
+λ=λ
+λ++λ+λ=λ
+λ++λ+λ=λ
+λ++λ+λ+λ=−Ιλ=λ
−−
−−
−
−−
−−
−
−
−−
.1)(
;)(
;)(
;)(
;)det()(
0
11
23
3
1
2
2
12
2
1
1
1
1
2
2
1
1
i
ii
nin
n
i
n
iin
nin
n
i
n
iin
nin
n
i
n
i
n
iin
d
ad
aaad
aaad
aaaaAd
Μ
Κ
Κ
Κ
(П.4.86)
Введем обозначения
.1,0 ;
)(
)(
)( −=
λ
λ
=λ
nj
d
d
d
in
ij
ij
(П.4.87)
Используя (П.4.85) и (П.4.87), выражение (П46.85) можно
представить в форме
()
[
]
{
}
0,1 );(|| | |
12
1
−=λΙ=−Ιλ
−
−
njdcolAAAA
ij
n
i
Κ . (П.4.88)
Тогда матрица
M
, записанная в форме (П.4.84), получает
представление
[
]
[
]
{
}
.,1 ;0,1 ;)(|| |
1
ninjHdcolrowBAABBM
iij
n
=−=λ−=
−
Κ (П.4.89)
Из (П.4.89) следует, что
1−
∃
M
, если
[
]
nBAABBrang
n
=
−1
|| | Κ , то
есть пара ) ,(
B
A
управляема.
Доказательство утверждения 3.3. Зададим желаемую структуру
мод
{
}
ni
i
,1 ; =λ и желаемую структуру собственных векторов
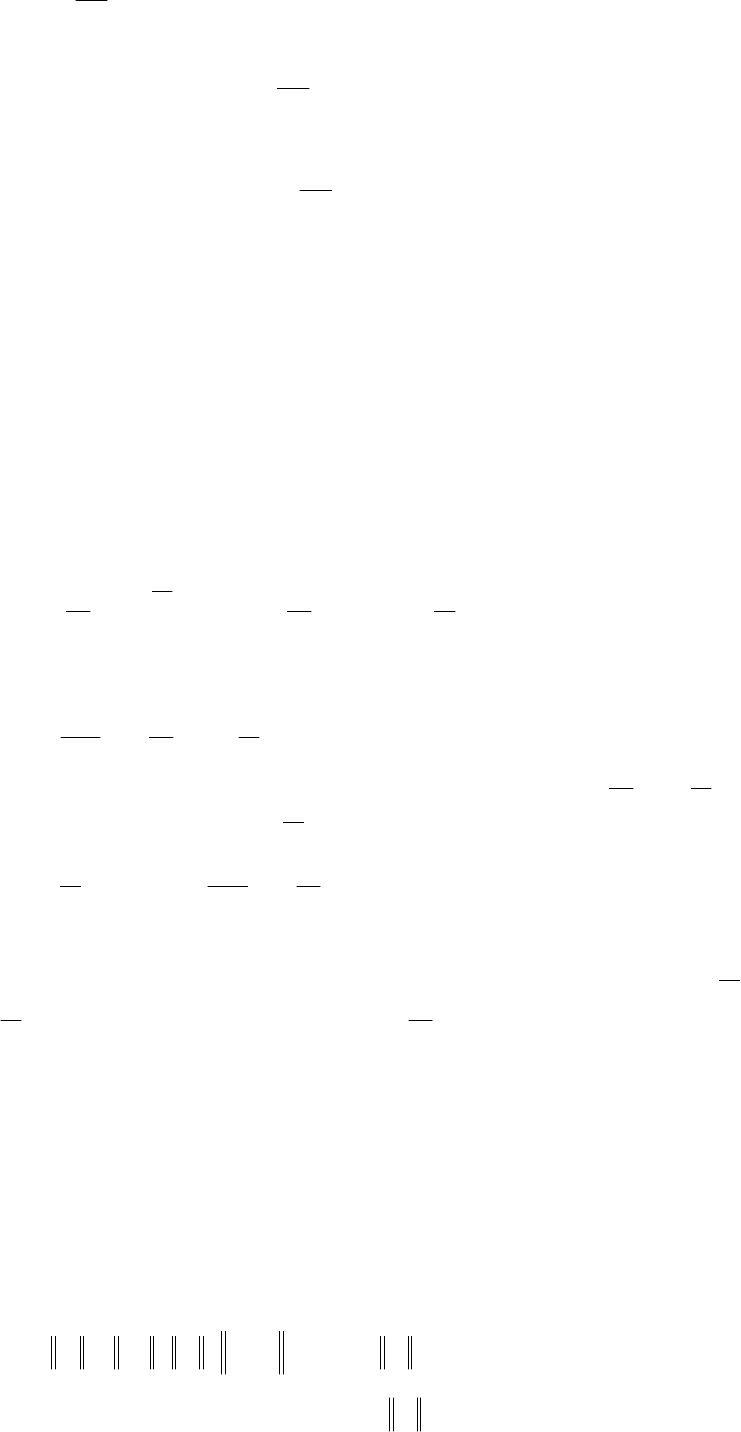
209
{
}
ni
i
,1 ; =ξ . Сконструируем на
i
λ
матрицу состояния ММ, заданную в
диагональной форме
{
}
nidiag
i
,1 ; ==Λ=Γ
λ
. (П.4.90)
Сконструируем матрицу
M
преобразования подобия в форме
{
}
niMrowM
ii
,1 ; =ξ== . (П.4.91)
Подставим (П.4.90) и (П.4.91) в уравнение Сильвестра (3.2).
Решим полученное уравнение относительно матрицы
H
, при этом,
если матрица
B удовлетворяет условию (3.7), то для
H
можно
записать
)(
1
Λ−=
−
MAMBH . (П.4.92)
Подстановка (П.4.92) в (3.1) приводит к (3.8).
Доказательство утверждения 3.4. Доказательство утверждения
строится на представлении матричного уравнения Сильвестра (3.2) в
форме
[] [][]
,
~
|
~
|
~
0
0
~
| HHBMMAMM −=−
⎥
⎦
⎤
⎢
⎣
⎡
Λ
Λ
(П.4.93)
которое декомпозируется на два матричных уравнения Сильвестра:
.
~
~
~
~
, HBMAMHBMAM −=−Λ−=−Λ
(П.4.94)
Первое из этих уравнений при заданных
M
и Λ решается
относительно матрицы
H
с учетом того, что n
r
rangB
<
=
в форме
()
()
.
1
MAMBBH
T
−Λ=
−
(П.4.95)
Второе уравнение Сильвестра (П.4.94) при заданных
(
)
H
~
,
~
Λ
,
решается относительно матрицы
M
~
. Композиция матриц
[
]
,
~
| HH где
H
имеет вид (П.4.95), и матриц
[
]
,
~
| MM подставленных в (3.1), дают
(3.9).
Доказательство утверждения 3.6. Доказательство утверждения
опирается на использование неравенства (3.22) и представление
матрицы
F
в форме
1−
Λ=
M
M
F
. (П.4.94)
Если в (П.4.94) осуществить переход к матричным нормам, то
получим неравенство
{
}
Λ=⋅Λ⋅≤
−
MCMMF
1
,
разрешив которое относительно
Λ
, получим:
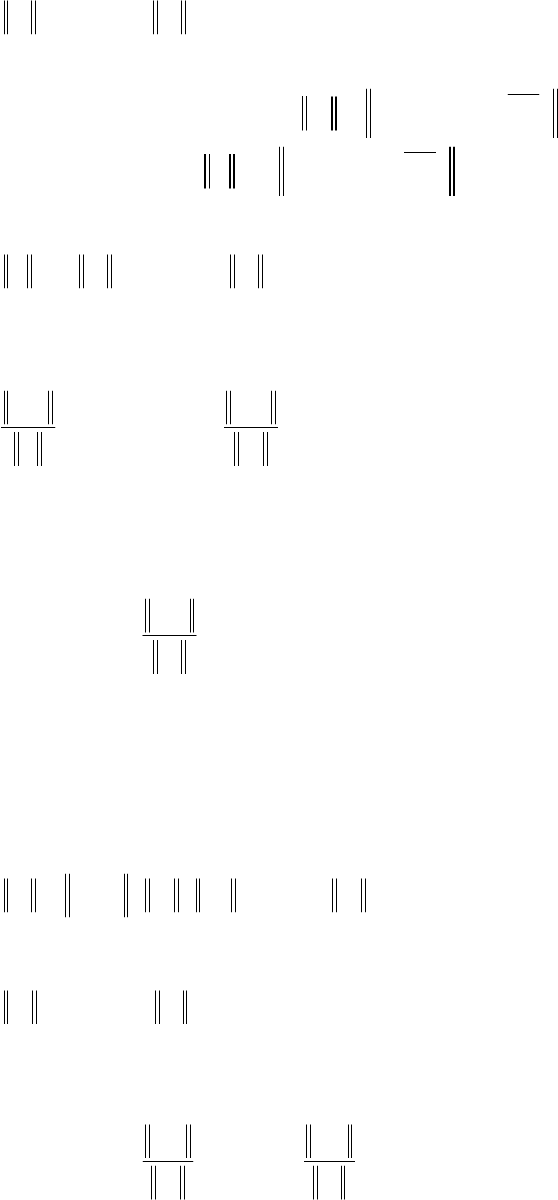
210
{}
FMC
1−
≥Λ . (П.4.95)
Учтем то обстоятельство, что все матричные нормы
диагональной матрицы
{
}
;1,
i
diag i nΛ= λ = совпадают с
бесконечной нормой
{
}
;1,
i
col i n
∞
λ= λ= вектора
λ
из собственных
значений матрицы
F так, что (П.4.95) можно записать:
{}
FMC
1−
∞
≥Λ=λ . (П.4.96)
Если теперь левую часть (3.22) поделить на левую часть (П.4.96),
а правую часть (3.22) – на правую часть (П.4.96), то получим:
{} {}
F
MC
F
F
MC δ=
Δ
≤δ=
λ
ΔΛ
λ
22
. ■(П.4.97)
Доказательство утверждения 3.7. Доказательство утверждения
основано на использовании (3.24), (П.4.97), а также равенства
A
F Δ=Δ , что в итоге позволяет записать неравенство
{}
F
F
MC
Δ
≤δ
λ
2
. (П.4.98)
Если теперь матричное соотношение (П.4.94) разрешить
относительно матрицы Λ в форме
FM
M
1−
=Λ , (П.4.99)
затем в (П.6.99) перейти к матричным нормам, то получим неравенство
{
}
FMCMFM =⋅⋅≤Λ
−1
. (П.4.100)
Неравенство (П.4.99) может быть записано в форме
{}
Λ≥
−
MCF
1
. (П.4.101)
Нетрудно видеть, что неравенства (П.4.98) и (П.4.101) позволяют
построить цепочку неравенств:
{} {}
Λ
Δ
≤
Δ
≤δ
λ
A
MC
F
A
MC
32
. (П.4.102)
Если в (П.4.102) ограничиться крайними слева и справа
элементами неравенства, то получим (3.26). ■
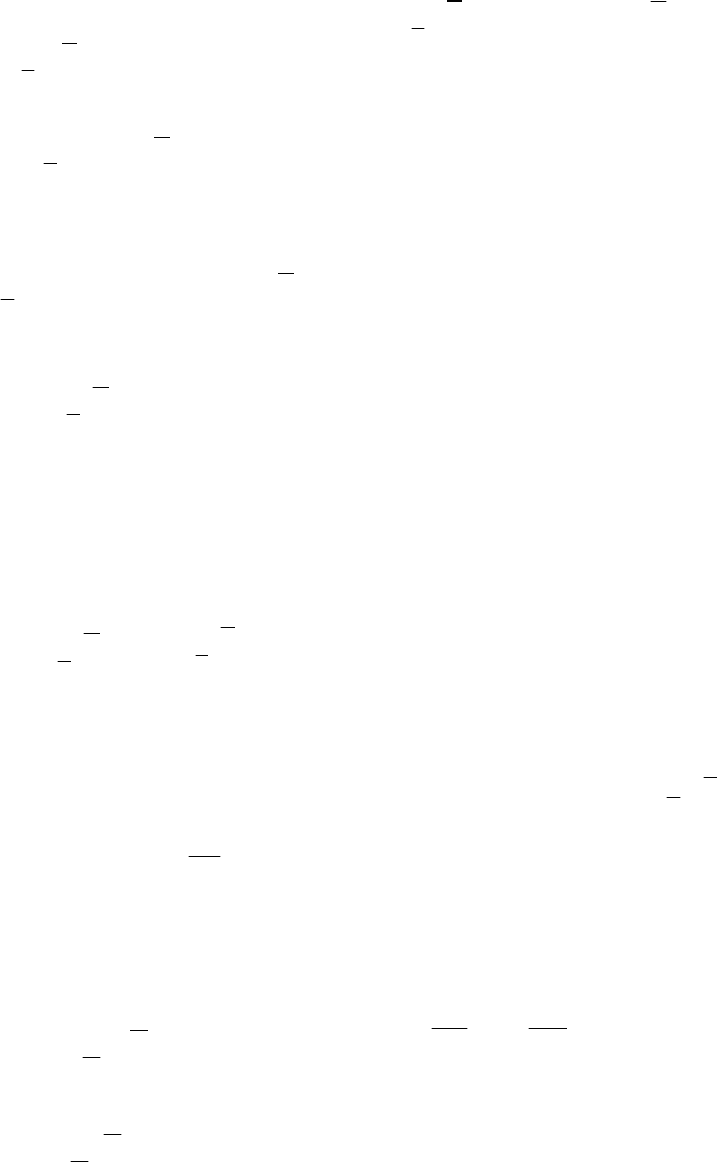
211
ПРИЛОЖЕНИЕ 5
Элементы интервальных вычислений
Определение П.5.1. Пусть числа ρ,
ρ
такие, что
f
,
R
∈ρ и при
этом
ρρ ≤ , задают вещественное число
ρ
в параметризованной
относительным параметром ]1,0[
∈
q форме
qq ρ
+
−ρ=ρ )1( , ((П.5.1)
Тогда вещественное интервальное число ][
ρ
образуется
экстремальными реализациями этого числа
{}
{
}
]1 ,0[ );(max ,]1 ,0[ );(min
∈
ρ
=
ρ
∈ρ=ρ qqqq
q
q
(П.5.2)
так, что оно может быть записано в форме
] ,[][ ρρ=ρ . □ (П.5.3)
Определение П.5.2. Интервальным комплексным числом
][ δ+ρ=γ
j
называется комплексное число, у которого интервальными
являются вещественная и мнимая части так, что становится
справедливым представление
][][][ δ+ρ
=
δ+ρ=γ
j
j
, (П.5.4)
где ] ,[][ ρρ=ρ ;
] ,[][ δδ=δ
. □
Ниже, в основном, рассматриваются вещественные интервальные
числа.
Определение П.5.3. Интервальным вектором ][
x
размерности n
называется вектор с интервальными компонентами
] ,[][
i
i
i
xxx = так,
что становится справедливой запись
{
}
nixcolx
i
,1 ];[][ == □ (П.5.5)
Определение П.5.4. Интервальной )( mn
×
-матрицей ][
A
называется матрица, составленная из интервальных скалярных
компонентов
] ,[][
ij
ij
ij
AAA = ,
(
)
{
}
mjAcolrowA
ij
,1 ;n1,i ];[[[ === (П.5.6)
при этом оказывается справедливым представление
] ,[][ AAA =
, (П.5.7)
где
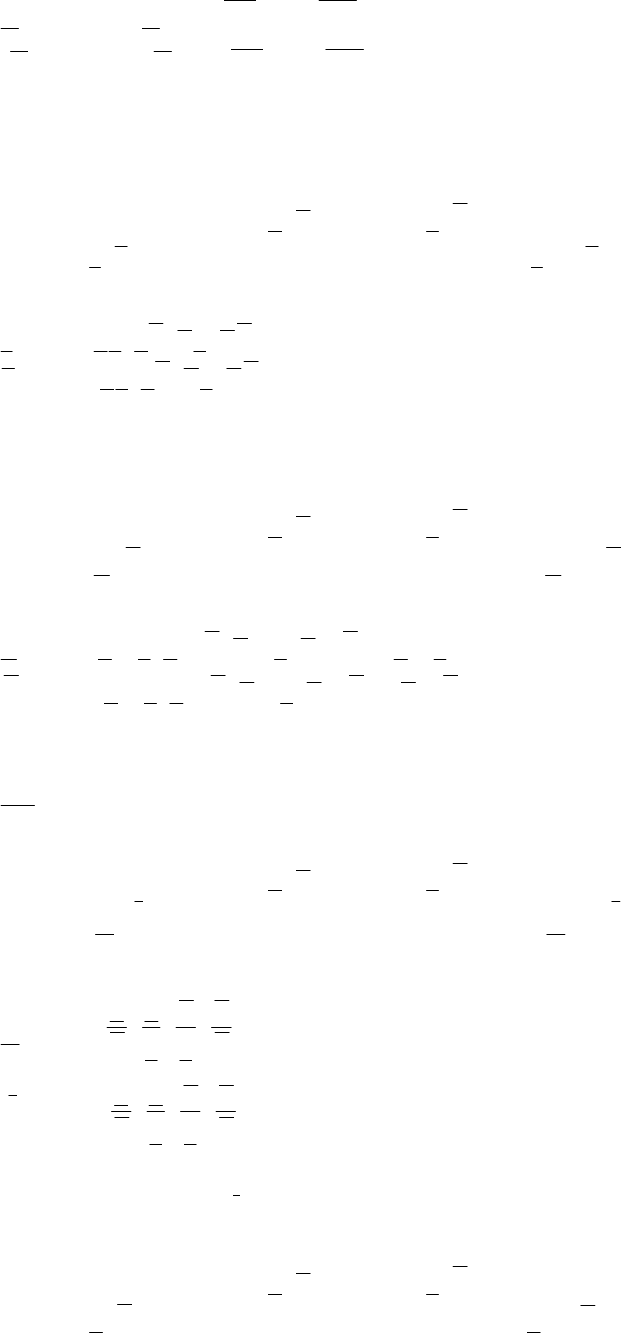
212
(
)
{
}
(){}
mjniAcolrowA
mjniAcolrowA
ij
ij
,1 ;,1 ;
,,1 ;,1 ;
===
===
□ (П.5.8)
Определение П.5.5. Произведением
][][][ cba =⋅ (П.5.9)
интервальных чисел ] ,[][ aaa = и
] ,[][ bbb
=
называется интервальное
число
] ,[][ ccc = , граничные значения которого c и
c
вычисляются в
силу соотношений
{
}
babababac , , ,min= , (П.5.10)
{
}
babababac , , ,max= . □ (П.5.11)
Определение П.5.6. Суммой
][][][ dba =+
(П.5.12)
интервальных чисел ] ,[][ aaa = и ] ,[][ bbb
=
называется интервальное
число
] ,[][ ddd = , граничные значения которого d и
d
вычисляются
с помощью соотношений
{
}
{}
. , , ,max
, , , ,min
bababababad
bababababad
+=++++=
+
=
+
+++=
□ (П.5.13)
Определение П.5.7. Частным от деления
][
][
][
f
b
a
=
(П.5.14)
интервальных чисел ] ,[][ aaa = и ] ,[][ bbb
=
называется интервальное
число
] ,[][ fff = , граничные значения которого f и f вычисляются
в силу выражений
. , , ,max
, , , ,min
⎭
⎬
⎫
⎩
⎨
⎧
=
⎭
⎬
⎫
⎩
⎨
⎧
=
b
a
b
a
b
a
b
a
f
b
a
b
a
b
a
b
a
f
□ (П.5.15)
Определение П.5.8. Разностью
][][][ hba =− (П.5.16)
интервальных чисел ] ,[][ aaa = и
] ,[][ bbb
=
называется интервальное
число
] ,[][ hhh = , граничные значения которого h и h определяются с
помощью выражений
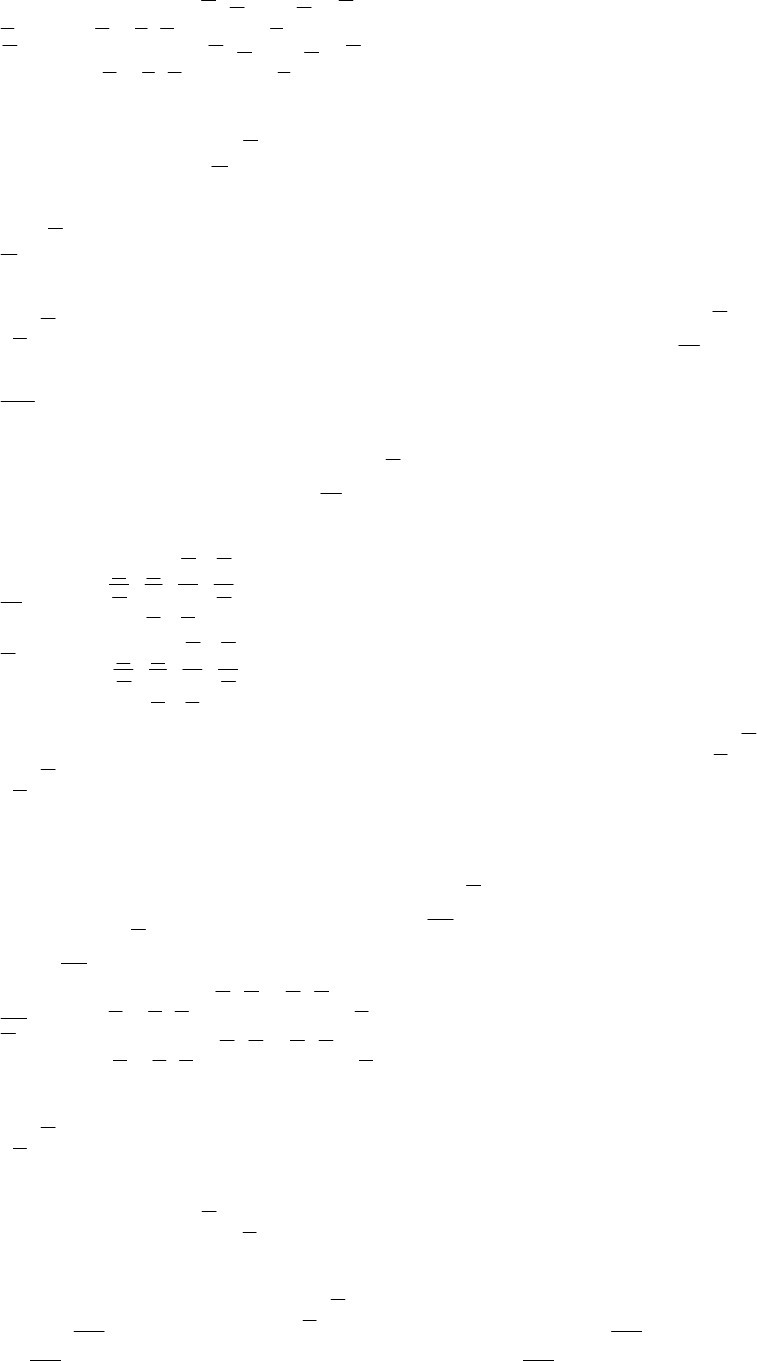
213
{
}
{}
. , , ,max
; , , ,min
babababah
babababah
−−−−=
−
−−−=
□ (П.5.17)
Определение П.5.9. Фиксированное число
g
имеет интервальное
представление
] ,[][ ggg = , которое характеризуется выполнением
равенства
gg ≡ . □ (П.5.18)
Утверждение П.5.1. Частное от деления интервального числа
] ,[][ aaa = на самое себя является интервальное число ]1 ,1[]1[
aaa
=
],1[
][
][
a
a
a
=
(П.5.19)
граничные значения которого
a
1 и
a
1 в силу (П.5.15) вычисляются с
помощью соотношений
. , , ,max1
, , , ,min1
⎭
⎬
⎫
⎩
⎨
⎧
=
⎭
⎬
⎫
⎩
⎨
⎧
=
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
(П.5.20)
Утверждение П.5.2. Разностью интервальных чисел ] ,[][ aaa = и
] ,[][ aaa =
]0[][][
a
aa =− (П.5.21)
является интервальное число ]0 ,0[]0[
aaa
=
, граничные значения
которого
a
0 и
a
0 в силу (П.5.17) задаются соотношениями
{}
{}
. , , ,max0
, , , ,min0
aaaaaaaa
aaaaaaaa
a
a
−−−−=
−
−−
−
=
(П.5.22)
Определение П.5.10. Медианой ][amid интервального числа
] ,[][ aaa = называется фиксированное число
0
a
, задаваемое
соотношением
()
aaaamid +
=
= 5.0][
0
. □ (П.5.23)
Определение П.5.11. Интервальным компонентом ][awid
интервального числа
] ,[][ aaa
=
называется интервальное число
] ,[][ aaa ΔΔ=Δ , граничные значения которого a
Δ
и a
Δ
задаются с
помощью соотношений
214
. ,
00
aaaaaa −=Δ−=Δ (П.5.24)
так, что ]. ,[][][
00
aaaaaaaawid −=Δ−=Δ=Δ= □
Утверждение П.5.3. Интервальное число ] ,[][ aaa
=
в силу
(П.5.23), (П.5.24), а также (П.5.13) и (П.5.18) представимо аддитивной
композицией
],[][
0
aaa Δ+= (П.5.25)
где
].[][ ],[
0
awidaamida =Δ=
Определение П.5.12. Медианой ][amid интервальной )( mn × –
матрицы
] ,[][ AAA = называется матрица
0
A с фиксированными
скалярными компонентами
oij
A
(
)
{
}
mjniAcolrowA
oij
,1 ;,1 ;
0
=== , (П.5.26)
где элементы
oij
A матрицы
0
A задаются соотношением
{
}
(
)
.5.0] ,[][
ij
ij
ij
ij
ijoij
AAAAAmidA
+
=
== □ (П.5.27)
Определение П.5.13. Интервальным матричным компонентом
][
A
wid
интервальной матрицы ] ,[][ AAA
=
называется интервальная
матрица
] ,[][ AAA ΔΔ=Δ , граничные реализации которой AΔ и
A
Δ
задаются соотношениями
(
)
{
}
(){}
.,1 ;,1 ;
,,1 ;,1 ;
00
00
mjniAAArowcolAAA
mjniAAArowcolAAA
ijijij
ijijij
==−=Δ=−=Δ
==−=Δ=−=Δ
(П.5.28)
так, что
] ,[][][
00
AAAAAAAAwid −=Δ−=Δ=Δ= . □
Утверждение П.5.4. Интервальная )( mn
×
-матрица ] ,[][ AAA = в
силу (П.5.26), (П.5.28), а также (П.5.27) и (П.5.8) представима в
аддитивной форме
],[][
0
AAA
Δ
+= (П.5.29)
где
].[][ ],[
0
AwidAAmidA =Δ=
Определение П.5.14. Произведением интервальных )( mn × -
матрицы
] ,[][ AAA = и )( km × -матрицы ] ,[][ BBB
=
][][][ C
B
A
=× (П.5.30)
называется интервальная )( kn
×
-матрица ] ,[][ CCC = с
интервальными скалярными элементами
] ,[][
il
il
il
CCC = ,
вычисляемыми в силу соотношений
