Никифоров В.О. и др. Интеллектуальное управление в условиях неопределенности
Подождите немного. Документ загружается.


130
с учетом представления матриц
M
, L и
Λ
как
{
}
MDrowM ,
=
,
{
}
LLrowL
D
,= ,
{}
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=ΛΛ=Γ=Λ
700
050
002
,
D
diag , ]2[
−
=
Λ
D
,
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=Λ
70
05
.
Уравнение
DD
BLADD −=
−
Λ решим при заданной матрице
[]
T
D 421 −= , в результате чего получим 4
=
D
L . Уравнение
LBMAM −=−Λ решим относительно
M
, задавая
[
]
11
=
L , тогда
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−=
6/14/1
42/120/1
294/101,0
M . Матрицы
M
и L исходного уравнения
Сильвестра (3.83) принимают вид
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−−=
61414
4212012
29410101
//
//
/,
M и
[]
114=L . Рассчитаем матрицу
K
обратной связи по формуле
1−
= MLK и получим
[]
135970=K . В соответствии с (3.84)
матрица
35
=
g
K
. Матрица состояния
F
номинальной версии
спроектированной системы принимает вид
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−−
=
145970
100
010
F ;
матрица
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−+−+−
−−
+
=
14459470
122
01
)(
qq
qq
qq
qF
. Проверим теперь,
является ли
D
собственным вектором
F
, воспользовавшись (3.106):
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−−
4
2
1
2
8
4
2
4
2
1
145970
100
010
. Т. о.,
D
является
собственным вектором матрицы
F
, соответствующим значению
2
1
−=λ
.
Проверим выполнение соотношения (3.105): произведение
матриц
[]
132=C и
[]
T
D 421 −= оказывается нулевым.
Следовательно, утверждения 1 и 4 выполняются, и
спроектированная система должна обладать параметрической
131
инвариантностью выхода, что означает равенство нулю функции
траекторной чувствительности )(
t
η
по выходу )(t
y
. Дополним модель
номинальной версии системы моделью траекторной чувствительности
к вариации параметра
q
и произведем моделирование полученной
агрегированной системы.
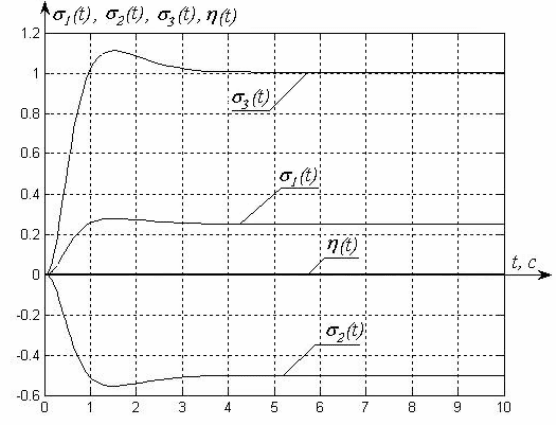
Результаты моделирования иллюстрируют равенство нулю
функции траекторной чувствительности по выходу
при единичном
ступенчатом (рис. 3.1) и гармоническом экзогенном задающем
воздействии
()
tg
(рис. 3.2).
Рис. 3.1 Функции траекторной чувствительности по состоянию и
выходу при 1)(
=
t
g
для параметрически инвариантной системы
Рассмотрим теперь контрпример. Сравним полученную систему
с системой, матрица состояния которой обладает спектром
собственных значений
{}
{
}
7;5;3
321
−
=
λ
−
=
λ
−
=
λ
=σ F
, при этом
утверждения 3.10 и 3.12 не выполняются. В этом случае матрицы
F
,
K
и
g
K принимают вид
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−−
=
1571105
100
010
F ,
[
]
1471105
=
K ,
632,52
=
g
K
. Результаты моделирования, представленные на рис.3.3,
показывают, что выход модели траекторной чувствительности не
равен нулю, то есть эта система не обладает параметрической
инвариантностью выхода относительно неопределенности параметров
132
ее матрицы состояния и вариация выхода примет вид
()()
qqtgty ΔΔ ,,,
0
=
()
(
)
0
,, qtgt
η
.0
0
≠
Δ
≠Δq
q
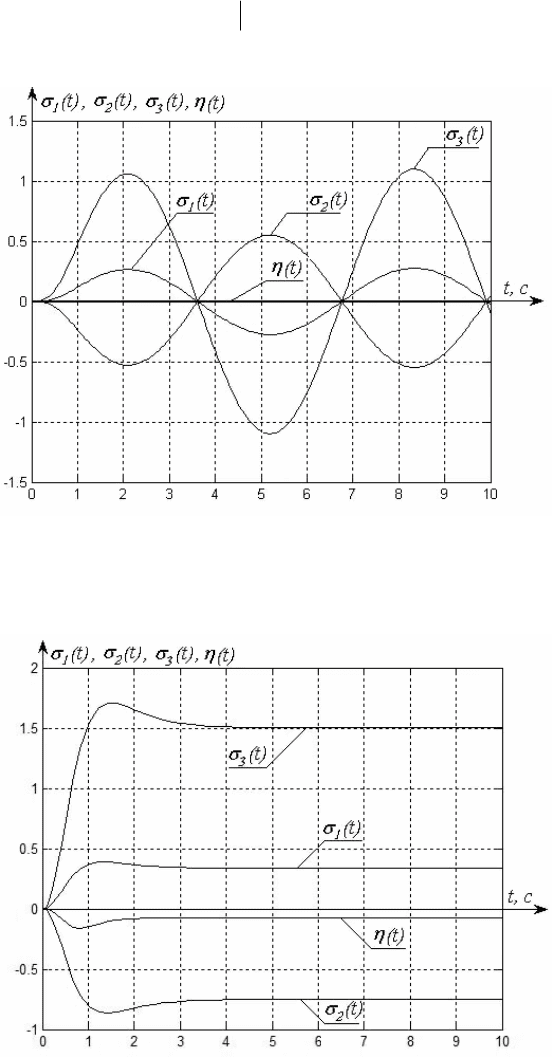
Рис. 3.2 Функции траекторной чувствительности по состоянию и
выходу при
tt
g
sin)( = для параметрически инвариантной
системы
Рис.3.3 Функции траекторной чувствительности по состоянию и
выходу при
1)(
=t
g
для параметрически неинвариантной
системы

133
Примечание. Для обеспечения желаемого левого собственного
вектора-строки
T
R
ς матрицы состояния системы
F
, соответствующего
собственному значению
ς
λ , можно предложить следующий алгоритм.
Предполагается, что заданы матрицы
{
}
ς
λ=λ−=λ=Λ
ni
nidiag ;1,1;
и
L
, желаемый левый собственный вектор
T
R
ς , обладающий единичной
нормой и соответствующий собственному значению
ς
λ
, требуемое
значение
Rς
Δ
невязки
TT
R
ςς
θ−ς=Δ
левых векторов матрицы
F
, пара
()
L,Λ
наблюдаема, размерность
L
равна размерности
T
B
.
Алгоритм 3.5.
Шаг1. Вычислить матрицу
{
}
niMBLAMMM
i
,1;1&arg ==−=−Λ=
.
Шаг 2. Вычислить матрицу состояния системы
F
=
1−
Λ
M
M
.
Шаг 3. Вычислить и произвести нормирование правого
собственного вектора
ς
θ матрицы
T
F
, соответствующего
собственному значению
ς
λ , обеспечив тем самым ему единичную
норму
.1=θ
ς
Шаг 4. Вычислить функцию
TT
R
ςς
θ−ς=Δ невязки
собственных левых векторов матрицы
F
.
Шаг 5. Проверить выполнение неравенства
Rςς
Δ
≤
Δ
, где
R
ς
Δ
–
требуемое значение невязки.
Шаг 6. Если неравенство шага 7 не выполняется, то с помощью
методов недифференцируемой оптимизации (метод
деформированного многогранника, Нелдера-Мида) сформировать
вариацию
()
kLΔ матрицы L , где
k
– номер итерации алгоритма, и
вернуться к шагу 1 алгоритма, в противном случае перейти к шагу 7.
Шаг 7. Вычислить матрицы формирователя сигнала
управления (ФСУ):
1−
=
LM
K
,
{
}
niMBLAMMM
i
,1;1&arg ==−=−Λ=
;
{
}
IBKCFK
gg
=
−
=
−1
arg
,
причем обратимость матрицы
F
обеспечивается тем, что все ее
собственные значения являются ненулевыми.
Шаг 8. Сформировать систему, образованную объединением
ОУ и ФСУ
() ()
(
)
tKxtgKtu
g
−
=
(
)
(
)
(
)
(
)
(
)
tCxtytGgtFxtx
=
+
=
,
&
, в
которой
g
BKGBKAF =−= ,
, при этом матрица
F
системы
обладает желаемым левым собственным вектором
T
R
ς
.

134
3.5. Робастное интервальное управление
Рассматриваются многомерные непрерывные объекты
управления, матричные компоненты векторно-матричного
представления которых характеризуются параметрической
неопределенностью, задаваемой в интервальной форме.
Предполагается, что модельная параметрическая неопределенность
может быть за счет выбора базиса или включения на входе буферной
системы с фиксированными параметрами представлена
неопределенностью (интервальностью) задания только матрицы
состояния объекта управления. Таким образом, объект управления
с
интервальными параметрами задается векторно-матричной моделью
()
[]
() () ( )
(
)
(
)
;0;
x
tAxtButx ytCxt=+ =
&
, (3.109)
где ,,
nr m
x
Ru Ry R∈∈∈– соответственно векторы состояния,
управления и выхода ОУ;
[
]
,,
A
BC– интервальная матрица
состояния, матрица управления и выхода, согласованные по
размерности с переменными модели (3.109). Для интервальной
матрицы
[
]
A
состояния используются два представления:
[]
()
{
}
()
{}
,: ;1,;1,;
;1,; 1,;
ij
ij
A
AA A rowcol A i n j n
ArowcolAi n j n
⎡⎤
== ==
⎣⎦
===
, (3.110)
[] [ ]
00
,
A
AAA AA
⎡⎤
=+Δ=+ΔΔ
⎣⎦
, (3.111)
где
()
{
}
0
0
;1,; 1,
ij
A
row col A i n j n===
, (3.112)
(
)
{
}
()
{}
;1,; 1,;
;1,; 1,;
ij
ij
A
row col A i n j n
Arowcol Ai n j n
Δ= Δ = =
Δ= Δ = =
(3.113)
000
0.5( ); ;
ij
ij
ij ij ij ij ij ij ij
A
AA AAA AAA=+Δ=−Δ=−
. (3.114)
В приведенных выражениях
00
,
ij
A
A
– медианные компоненты
соответственно интервальных матрицы
[
]
A
и ее
(
)
,ij
-го компонента
ij
A
⎡⎤
⎣⎦
;
[
]
,
ij
AA
⎡⎤
ΔΔ
⎣⎦
– интервальные матричный элемент и его
(
)
,ij
-й
скалярный компонент, задающие ширину
[
]
(
)
(
)
,
ij
wid A wid A
⎡
⎤
⎣
⎦
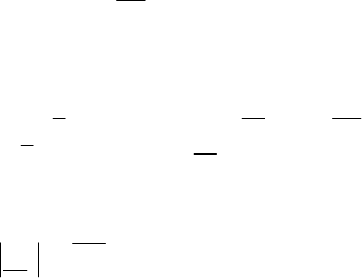
135
соответственно интервальной матрицы
[
]
A
и ее
(
)
ji,-го
интервального скалярного компонента
ij
A
⎡
⎤
⎣
⎦
. Будем именовать
0
A
и
[]
A
Δ
соответственно медианой и интервальной составляющей
интервальной матрицы
[]
A
Δ
.
Ставится задача синтеза неадаптивного регулятора,
реализующего закон управления в виде обратной связи с матрицей К
по состоянию x(t) и прямой связи с матрицей
g
K
по внешнему
задающему воздействию g(t), записываемый в форме
() () ()
g
ut K gt Kxt=−
. (3.115)
Здесь
,
g
K
K
– матрицы с фиксированными параметрами, так что их
интервальные представления
[
]
[
]
,, ,
ggg
K
KK K KK
⎡⎤⎡ ⎤
==
⎣⎦⎣ ⎦
характеризуются медианами
00
,
gg
K
KK K
=
=
и нулевой шириной
[]
0, 0
g
wid K wid K
⎡⎤
==
⎣⎦
. Закон управления (3.115) должен доставить
системе
[]
() () (); (0); () ()
x
tFxtGgtxytCxt=+ =
&
, (3.116)
образованной агрегированием ОУ (3.109) и ЗУ (3.115), значения
показателей
{
}
;1,I
ρ
ρ
=
μ
качества процессов в переходном и
установившемся режимах, которые, будучи интервальными и
представимыми в формах
0
,,;(1,)
ρ
ρ
ρρρρ
⎡⎤
⎡⎤
⎡⎤
π=ππ=π+ΔπΔπ
ρ
=
μ
⎣⎦
⎣⎦
⎣⎦
,
удовлетворяли бы по медианной составляющей квалификационному
неравенству
00R
ρ
ρ
π≤π
и характеризовались шириной
22wid
ρ
ρρ
⎡⎤
π=Δπ=Δπ
⎣⎦
, которая удовлетворяет технологический
процесс, в который встраивается проектируемая система.
Основная часть публикаций, связанных с проблемами синтеза
законов неадаптивного управления вида (3.115), использует
формулировку задачи синтеза, сводящую ее к проблеме робастной
устойчивости, факт достижения которой контролируется методом
В.Л. Харитонова. Необходимо отметить, что при представлении
интервальных матриц в основном, за редким
исключением,
используется форма (3.110).
136
Вернемся к модели (3.116) спроектированной системы, в которой
для интервальной матрицы состояния
[
]
F
запишем
[] []
0
,
F
FF F F
⎡⎤
==+Δ
⎣⎦
, (3.117)
[][] [ ]
[
]
00
F
ABKA ABKABK A= − =+Δ− =− +Δ. (3.118)
Матричные соотношения (3.87), (3.88), по существу, содержат
доказательство следующего утверждения.
Утверждение 3.13. Закон управления вида (3.115) изменяет
лишь медианную составляющую
0
F
интервальной матрицы
[]
F
состояния системы (3.116) в силу соотношения
00
F
ABK=−
, (3.119)
оставляя неизменной ее интервальную составляющую так, что
выполняется равенство
[
]
[
]
F
AΔ=Δ
. ■ (3.120)
Отметим важное свойство интервальной составляющей
[
]
()
Δ
∗
интервальной матрицы
[
]
()∗ .
Свойство 3.1. Норма
[]
()
Δ
∗ интервальной составляющей
[]
()Δ∗ интервальной матрицы
[
]
()
∗
не является интервальной и
совпадает с нормой любой ее угловой реализации
{( ( )) } ; 1,2
nn
c
×
ν
Δ∗ ν=
так, что выполняется равенство
()
{( ( )) } ; 1,2
nn
c
×
ν
Δ∗ = Δ∗ ν=
⎡⎤
⎣⎦
. (3.121)
Теперь введем две характеристики интервальной матрицы
[
]
()∗ ,
задав их с помощью определений.
Определение 3.5. Оценкой абсолютной интервальности
интервальной матрицы
[]
[
]
0
() () ()∗=∗+Δ∗
называется положительное
число
()
I
Δ∗
, задаваемое соотношением
() [ ()]
I
Δ
Δ∗=Δ∗
. (3.122)
Определение 3.6. Оценкой относительной интервальности
интервальной матрицы
[]
[
]
0
() () ()∗=∗+Δ∗ называется положительное
число
()
I
δ∗

137
00
[()]
()
()
() ()
I
I
Δ
Δ∗
Δ∗
δ∗= =
∗∗
. □
Нетрудно видеть, что введенные оценки интервальности
интервальной матрицы
[]
()∗ применительно к
[
][]
()
F
∗
=
интервальной матрице состояния спроектированной системы (3.116)
совместно с положениями утверждения 3.13 содержат доказательство
следующего утверждения.
Утверждение 3.14. Закон управления (3.115) не изменяет
значения оценки абсолютной интервальности матрицы состояния, так
что выполняется равенство
I
I
F
AΔ=Δ
, (3.123)
но при этом изменяется значение оценки относительной
интервальности интервальной матрицы
[
]
F
состояния системы (3.116)
в силу соотношения
00
[] []
I
AA
F
F
ABK
ΔΔ
δ= =
−
. ■
Теперь сформулируем постановку задачи синтеза закона
управления объектом с интервальными параметрами –
сконструировать матрицы
K
и
g
K
закона управления (3.115) такие,
чтобы:
1.
медианная составляющая
00
F
ABK
=
−
матрицы
[]
F
спроектированной системы (3.116) доставляла медианные
значения
()
0
1,
ρ
π
ρ
=
μ
показателей качества процессов в
переходном и установившемся режимах, удовлетворяющих
требованиям
()
00
1,
Rρρ
π≤π
ρ
=
μ
; (3.124)
2.
оценка относительной интервальности
I
F
δ
матрицы
[]
F
состояния спроектированной системы (3.116) удовлетворяла
условию
I
IR
F
Fδ≤δ
, (3.125)
при этом
I
R
F
δ
была такой, что становится корректным
использование аппарата теории чувствительности в рамках
функций чувствительности первого порядка;

138
3.
для медианной составляющей
0
F
матрицы состояния
[]
F
выполнялось условие обеспечения единичного отношения
"вход – выход" в неподвижном состоянии
() ( )
{
}
(
)
1
1
1
00 0
0
arg
gg
s
K
sCsIF BK I CFB
−
−
−
=
=Φ= − ==− . (3.126)
Для решения поставленной задачи воспользуемся
возможностями обобщенного модального управления (ОМУ). При
этом, как указывалось ранее, в зависимости от ранга матрицы B ,
когда ранг матрицы Bn= , возможно решение полной задачи ОМУ
так, что свободно назначаются желаемые спектры собственных
значений медианной версии
{
}
{
}
0
;1,
i
F
inσ=λ= матрицы
F
системы
и собственных векторов
{
}
0
:;1,
ii
M
MFMinξ= Λ= = этой матрицы. В
противном случае, когда rangB r n
=
〈 , возможно решение неполной
задачи ОМУ, в которой назначается спектр
{
}
0
F
σ
, а матрица
M
собственных векторов
{
}
0
;;1,
ii iii
M
row M F i n==ξξ=λξ= ищется из
соображений
{
}
{
}
arg min
M
CM= . (3.127)
Напомним, что потребность контролировать число обусловленности
{
}
CM матрицы собственных векторов вызвана поиском возможности
априори с помощью оценки нормы
Λ
матрицы состояния
модальной модели, задаваемой наблюдаемой парой
(
)
,
H
Λ
, оценить
норму
00
F
ABK=− с тем, чтобы удовлетворить требованию (3.125).
В основу этой оценки кладутся соотношения матричного
подобия
0
M
FMΛ= , (3.128)
которые в нормах приводят к оценочным неравенствам
{
}
{
}
1
0
CM F CM
−
Λ≤ ≤ Λ
, (3.129)
и требованию (3.125), записываемому в силу (3.129) в виде
0
[]
I
IR
A
F
F
A
∑
Δ
δ= ≤δ
. (3.130)
Объединение (3.129) и (3.130) порождает цепочку неравенств

139
{}
[]
0
[]
I
IR
A
A
FCM F
F
Δ
Δ
δ= ≤ ≤δ
Λ
. (3.131)
Правая часть неравенства (3.131) приводит к оценке требуемой
нормы
Λ матрицы состояния ММ
{}
[]
I
R
A
CM
F
Δ
Λ≥
δ
. (3.132)
Полученные соотношения позволяют предложить алгоритм синтеза
закона управления в виде (3.115) методами обобщенного модального
управления для случая rang B n= .
Алгоритм 3.5
1. Построение
(
)
,,
A
BC представления ОУ в базисе, в котором
интервальность первичных физических параметров приводит к
интервальности только матрицы состояния так, что объект
получает
[]
()
,,ABC представление. Запись интервальной
матрицы
[]
A
в форме
[
]
[
]
0
A
AA=+Δ
.
2. Формирование требований к показателям качества процессов в
переходном и установившемся режимах в виде набора их
медианных значений
(
)
{
}
0
1,
ρ
π
ρ
=
μ
для системы с медианной
матрицей состояния
0
F
, а также задания требуемой величины
I
R
F
δ оценки относительной интервальности интервальной
матрицы
[]
F
проектируемой системы
0
[]
I
IR
A
F
F
F
Δ
δ
=≤δ.
3.
Формирование требований к матрице состояния
Λ
модальной
модели, задаваемой в диагональной форме
{
}
;1,
i
diag i nΛ= λ =
со структурой и реализацией
i
λ
, доставляющих системе набор
требуемых показателей качества
(
)
{
}
0
1,
ρ
πρ
=
μ
, образующих
вектор
0
π
так, что
(
)
0
Λ=Λ π
.
4.
Формирование матрицы
Λ
модальной модели со структурой
мод п. 3 алгоритма, но с нормой
Λ
при известной
[
]
A
Δ
норме интервальной составляющей матрицы состояния
[
]
A
ОУ
(3.109) в силу (3.131), в котором в силу достижимости
