Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

11.1. МЕХАНИЗМЫ РЕКУРСИИ

635

дов, основанных на рекурсии, мы преимущественно будем придерживаться

стиля структурного программирования. Это позволит давать более прямые

и реалистичные по отношению к существующим реализациям оценки алго-

ритмов.

§ 11.1. МЕХАНИЗМЫ РЕКУРСИИ

При обсуждении подпрограмм уже говорилось о рекурсивных процеду-

рах. Была указана связь рекурсивных алгоритмов с рекуррентными соотно-

шениями между данными. По существу это основа обширного класса ре-

курсивных методов, которые можно охарактеризовать как проецирование ре-

куррентности на программу. Но рекуррентное соотношение является лишь

предпосылкой к тому, чтобы строить рекурсивную программу. В частности,

рекурсивная программа проигрывает итеративной схеме по эффективности,

когда конкретная задача фактически не требует дополнительной памяти, во-

влекаемой в вычисления при рекурсии. Именно здесь, где целесообразно ди-

намически выделять и освобождать память, но можно сделать это без явного

обращения к механизмам распределения памяти, проходят границы разум-

ного применения рекурсивных методов

Подводный камень рекурсии, также рассмотренный ранее, — повторный

счет. Мы увидели это на примере прямолинейной реализации рекуррентно-

го соотношения. В реальной практике подобное встречается и в более заву-

алированной форме, что, собственно говоря, и приводит к отрицательному

отношению к рекурсии среди программистов, привыкших к операционным

моделям вычислений. Если же обратиться к функциональному программи-

рованию, то, во-первых, среди его приемов есть достаточно полезные сред-

ства преодоления повторения вычислений, а во-вторых, автоматический ана-

лиз программ этого стиля, направленный на выявление повторений, гораздо

легче и продуктивнее, чем для императивных программ. Тем не менее, опас-

ность повторного счета остается всегда.

Методы, основанные на рекурсии, укладываются в следующую универ-

Заманчиво выглядят применения автоматической трансформации рекурсивной програм-

мы в итеративную, когда дополнительная память фактически нужна лишь для организации

рекурсивных вызовов. Однако соответствующие алгоритмы довольно трудны и далеко не

всегда распознают ситуацию, а потому такой путь нельзя рекомендовать как универсаль-

ный. К тому же, если программист составляет рекурсивный алгоритм по той причине, что

он просто не проанализировал реальную потребность в ресурсах для решаемой задачи, то

это свидетельствует о его низкой квалификации. И очень часто такой анализ прямо ведет

разработчика к ручной трансформации решения.

636

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

сальную схему.

Определение 11.1.1. Пусть Σ — набор данных, обрабатываемых при вы-

полнении некоторого действия ∆(Σ). Σ рассматривается как обстановка вы-

числений действия ∆ (см.п.7.3.5и §8.3),и,таким образом,она может включать

как входные данные, так и результаты вычислений: ∆

∪∆

Out

(∆

∩∆

Out

= ∅

не обязательно выполнено). Если даны наборы данных Σ

, ..., Σ

, действия

∆

, ..., ∆

, и схема программ Ω над ∆

(Σ

), ..., ∆

(Σ

), с входными данны-

ми ∆

и результатами ∆

Out

, такая, что:

• выполнение Ω приводит к выполнению ∆(Σ) в целом;

• каждое из ∆

является либо атомарным, либо в свою очередь описано

через декомпозицию;

• среди ∆

, ..., ∆

или среди реализующих их схем представлено один

или более раз ∆;

то ∆ называется рекурсивным, а Ω называется рекурсивной схемой программ

для ∆(Σ). Ω называется также декомпозицией ∆(Σ), а ∆

(Σ

), ..., ∆

(Σ

) —

базисом этой декомпозиции.

Конец определения 11.1.1.

Применение этого определения требует конкретизации большинства затра-

гиваемых им понятий. Во-первых, схема Ω здесь не обязательно схема про-

грамм в классическом смысле. Она может включать и совместные, и недетер-

минированные, и параллельные действия. Во-вторых, отнюдь не все элемен-

ты обстановки могут представляться реальными программными объектами,

они могут (и часто должны быть) призраками.

Рассмотрим пример. Если пополнить входные данные программы всеми

их возможными комбинациями при помощи имеющихся функций (постро-

ить т. н. сколемовский универс), то можно считать все Σ

подмножествами

Σ. Но такое разбиение данных, хотя полезно для анализа программы, в боль-

шинстве случаев остается лишь концептуальным, и нет нужды строить его

явно: это не только нецелесообразно, но зачастую и просто невозможно. Бо-

лее того, если явное построение осуществимо, а не остается призраком, то

именно это свидетельствует о том, что, по-видимому, в данном случае более

разумно итеративное решение, которое не нуждается дополнительной памя-

ти рекурсивного вычисления.

В то же время, необходимо научиться выстраивать последовательность

данных (наборов данных), которая будет динамически предъявляться ∆

, ...,

11.1. МЕХАНИЗМЫ РЕКУРСИИ

637

∆

при каждом обращении к рекурсивно задаваемому действию. С разбие-

нием действий чуть проще: это, собственного говоря, и есть декомпозиция

алгоритма. Основные задачи здесь сводятся к следующему. Надо понять, что

именно будет предохранять от бесконечного вычисления рекурсивных схем

и от повторного счета.

Определение 11.1.2. Пусть Ω рекурсивная схема для ∆(Σ) с базисом ∆

(Σ

..., ∆

(Σ

), пусть Ex —исполнение данной схемы. Пусть j1 — номер компо-

нента базиса, для которого ∆

(Σ

) присутствет в исполнении и приводит к

исполнению ∆(Σ

). Тогда можно построить рекурсивную схему следующего

уровня, совпадающую с Ω по структуре, но имеющую базис

∆

(Σ

), . . . , ∆

(Σ

Таким путем может быть выстроена последовательность активизаций ∆, на-

зываемая путем рекурсии:

∆(Σ) = ∆(Σ

), ∆

(Σ

), ∆(Σ

) . . . , ∆(Σ

), ∆

(Σ

), ∆(Σ

k+1

), . . . . (11.1)

Если эта последовательность конечна, т. е. существует k такое, что в испол-

нении ∆(Σ

) уже нет компонент, исполняющих ∆, то номер j, 1 6 j 6 k,

называется уровнем рекурсии, а k — глубиной рекурсии для исполнения Ex.

Рекурсивная схема называется конечной, если для всех данных, с которы-

ми выполняется ∆, гарантируется конечность глубины рекурсии. Рекурсив-

ная схема называется избыточной, если существует набор данных, с кото-

рыми выполняется ∆, для которого в последовательности (11.1) встречают-

ся повторяющиеся элементы. Рекурсивная схема называется слабо избыточ-

ной,если существует набор данных,с которыми выполняется ∆,для которого

на двух путях рекурсии (11.1) встречаются повторяющиеся элементы.

Конечная и не избыточная рекурсивная схема называется слабо коррект-

ной. Конечная, не избыточная и не слабо избыточная рекурсивная схема на-

зывается корректной.

Конец определения 11.1.2.

Нужно всегда знать,чем в конкретном случае становятся контексты компонет

рекурсивного вызова, а также обосновывать, что рекурсивная схема является

корректной. Следующие примеры поясняют данное определение.

Пример 11.1.3. Разбиение данных и действий.

Процедура рекурсивного вычисления факториала (см. программу 8.7.1 на

стр. 464) приводит к следующим контекстам данных и разбиениям действий:

638

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

∆

= {N | (N < 2)} =⇒

result

= 1

;

= {1,

result

};

∆

= {N | (N > 2)} =⇒

result

Fact (N-1);

= {N − 1,

result

}

;

∆

= =⇒

result

(∆

) ∗ N

;

= {

result

(∆

) ∗ N}

;

Для дальнейших уровней рекурсии выражения остаются совершенно анало-

гичными выражениям для ∆

, Σ

Разбиение аргумента

остается призраком. Оно представляет базу для

соответствующих действий, второе из которых задает рекурсию, а третье –

синтезирует результат. Условие из программы 8.7.1 и зависимость ∆

N+1

от

∆

гарантируют сильную корректность схемы. Путь рекурсии всего один.

Конец примера 11.1.3.

Анализ разбиений данных и контекстов действий является мощным инстру-

ментом для сложных рекурсивных программ, но он требует во всех нетриви-

альных случаях дополнения аппаратом т. н. сигнализирующих функций.

На практике непосредственная проверка конечности глубины рекурсии

может оказаться затруднительной. Поэтому, согласно парадоксу изобрета-

теля, нужно вводить идеальные конструкции, гарантирующие конечность.

Первое, что здесь приходит на ум — ввести некоторое частичное упорядоче-

ние  на множестве контекстов Σ, такое, что на любом пути рекурсии

 Σ

 ···  Σ

 ···

Это отношение лучше всего задать при помощи функции-призрака, отобра-

жающей множество контекстов в какое-либо обычное частично-упорядочен-

ное (а чаще всего в линейно-упорядоченное) множество. Такая функция на-

зывается сигнализирующей функцией рекурсии. Итак, для сигнализирующей

функции ϕ должно на каждом пути рекурсии выполняться

ϕ(Σ

)  ϕ(Σ

k+1

j(k+1)

Когда ϕ становится достаточно малой (например, доходит до нуля), рекурсия

заканчивается. На самом деле ϕ может принимать в качестве аргумента лишь

входные части контекстов.

Но даже это не всегда гарантирует конечности. Пусть, например, значе-

ниями ϕ являются рациональные числа и на пути рекурсии она выдает убы-

вающую последовательность

, . . . ,

, . . .

11.1. МЕХАНИЗМЫ РЕКУРСИИ

639

Сами видите, что такая рекурсия бесконечна. К счастью, в логике накоплен

багаж фундированных чумов, в которых любая убывающая последователь-

ность конечна. Самым часто применяемым из них является множество орди-

налов (см., например, [63]). Для построения сигнализирующей функции для

любой практической программы достаточно ординалов до ε

. Другим полез-

ным примером фундированного чума является лексикографически упорядо-

ченная последовательность n-ок натуральных чисел.

Пример 11.1.4. Корректность процедуры

MCD

и избыточность функции

из § 8.7.

Проанализируем процедуру

MCD

(программа 8.7.3),предназначенную для

вычисления наибольшего общего делителя двух чисел. Воспользуемся од-

ним из стандартных решений: лексикографическим порядком на парах на-

туральных чисел. Каждая из входных частей

(Σ

) множеств Σ

является

парой чисел, и очевидна монотонность последовательности

(Σ

). таким

образом, здесь сигнализирующая функция просто выделяет входную часть

Σ. Отсутствие избыточности вычислений обеспечивается структурой зави-

симостей действий процедуры, благодаря которой последовательность (11.1)

не содержит повторений. В функции

(процедура 8.7.2), вычисляющей чи-

сла Фибоначчи, действия в синтезирующей части схемы (сложение двух ре-

зультатов) прямо указывают на повторное появление рекурсивно вызывае-

мых действий на различных путях рекурсии. Это повторение появляется в

связи с тем, что от каждого уровня рекурсии возникают по две независимых

друг от друга последовательности вызовов, а потому внутри каждой из них

нет способа узнать о повторениях вычислений на другой последовательно-

сти. Но каждый из путей рекурсии упорядочен отношением < для аргумен-

тов вызовов функции, и эта процедура слабо корректна.

Конец примера 11.1.4.

При задании рекурсивных алгоритмов важно хорошо представлять, в какой

последовательности выполняются действия

∆

(Σ

), . . . , ∆

(Σ

относящиеся к разным уровням рекурсии. От этого порядка, в частности, за-

висит накапливаемый результат вычислений, и, если не заботиться о нем,

то выходные данные будут порождаться, но совершенно не соответствую-

щие тому, что требуется. На рис. 11.1 приводится схема, иллюстрирующая

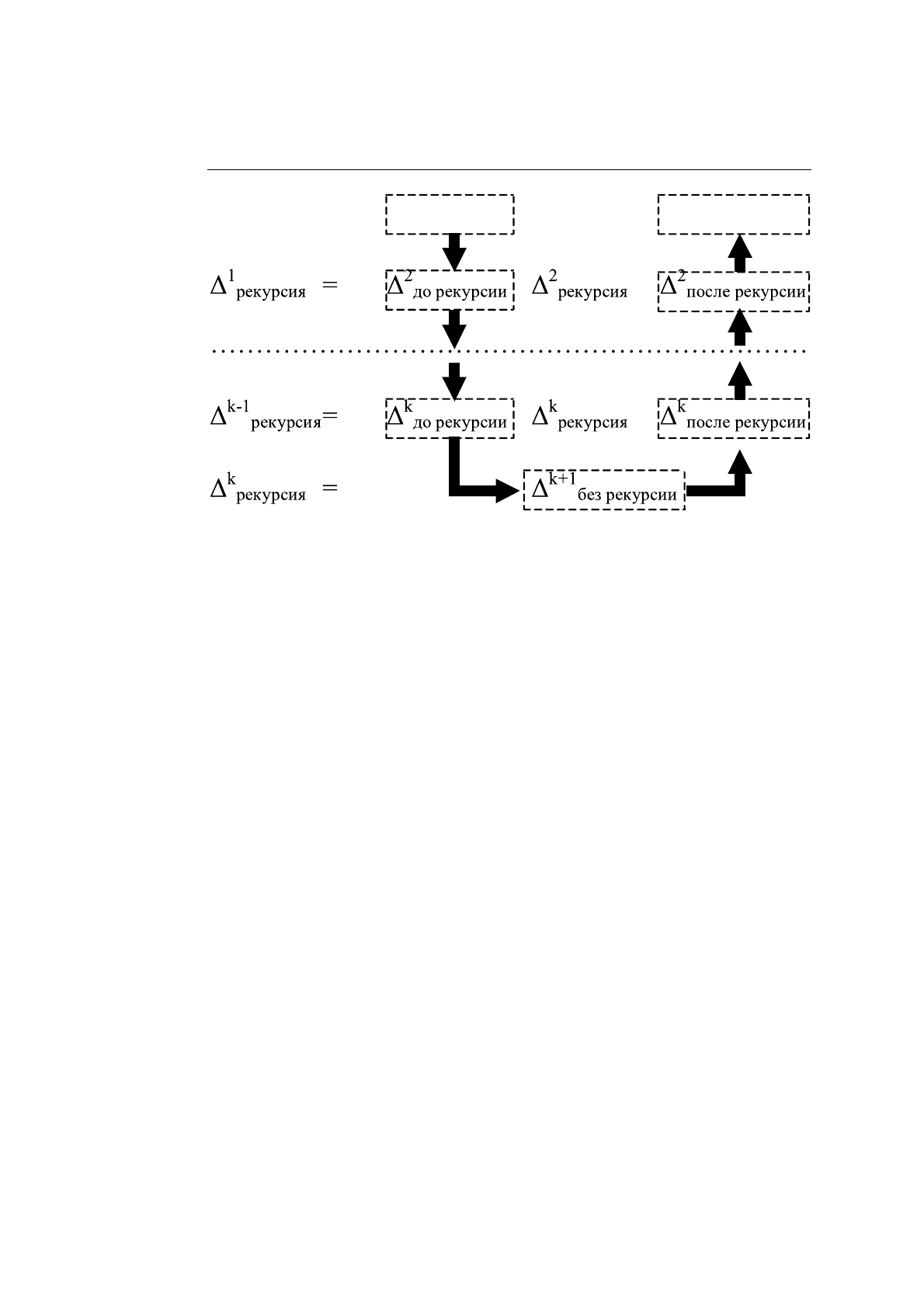
640

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

∆

до рекурсии

∆

рекурсия

∆

после рекурсии

Рис. 11.1. Порядок действий при использовании рекурсии

порядок исполнения действий из разбиений, относящихся к разным уров-

ням рекурсии. Он показан стрелками, соединяющими элементы разбиений

(пунктирные блоки).

Определение 11.1.5. При последовательной организации рекурсивных вы-

числений их порядок задается как один из следующих вариантов рекурсив-

ных схем:

• префиксная схема,когда делается попытка сначала выполнить действие

∆ (т. е. первое исполняемое действие из ∆

, ..., ∆

приводит к ∆), а

затем выполняются остальные действия;

• постфиксная схема, когда сначала выполняются все действия из ∆

..., ∆

, не приводящие к ∆, после чего делается попытка выполнить

действие ∆

, которое приводит к ∆;

• инфиксная схема, когда попытке выполнить действие ∆ предшествует

некоторое число действий из ∆

, ..., ∆

, а после выполнения ∆ выпол-

няются остальные действия;

• смешанные схемы — комбинации предыдущих случаев.

Конец определения 11.1.5.

11.2. ЗАКРАШИВАНИЕ ЗАМКНУТЫХ ОБЛАСТЕЙ

641

Постфиксная схема обладает свойством, которое на первый взгляд может по-

высить эффективность выполнения рекурсивных программ: за счет того, что

после выполнения действия на максимальной глубине рекурсии, нет дей-

ствий других уровней рекурсии, которые требуется выполнить, можно по-

следовательный возврат по уровням заметить завершением сразу всей цепоч-

ки рекурсивных вызовов. Однако при ближайшем рассмотрении становится

ясным, что в общем случае здесь никакого выигрыша нет. В обоих случаях

корректное завершение требует последовательной ликвидации в обратном

порядке (см. рис. 11.1) процессов, порожденных на каждом уровне рекур-

сии, а это как раз то, что происходит при последовательном возврате. В то же

время явное указание возможности завершения всех уровней рекурсии сразу

может повысить выразительность алгоритма.

При префиксной схеме в принципе возможно бесконечное углубление ре-

курсии, если не гарантируется, что данные, поставляемые для переработки

на каждый новый уровень рекурсии, ведут к некоему пределу, обеспечива-

ющему конечность уровней. Для этого предела должно быть предусмотрено

действие, которое уже не приводит к рекурсии. При использовании инфикс-

ной и постфиксной схем оба эти условия можно выполнить за счет начальных

действий, предшествующих рекурсии.

Рассмотренные выше положения никак не привязаны к моделям вычи-

слений языков. Здесь выделено то, что в полной мере присуще как опера-

ционному стилю структурного программирования, так и неимперативному

функциональному стилю. По существу, речь идет об алгоритмах, т. е. о том,

что нужно иметь ввиду программисту, когда он намерен применять в своей

практике методы, основанные на рекурсии.

§ 11.2. ЗАКРАШИВАНИЕ ЗАМКНУТЫХ ОБЛАСТЕЙ

Первая задача, на примере которой можно показать продуктивность при-

менения методов, основанных на рекурсии относится к области, где они ис-

ключительно широко применяются: машинной графике.При оперировании с

изображениями зачастую возникает потребность закрашивать части экрана,

которые содержательно соответствуют областям плоскости, ограниченным

замкнутыми кривыми. Необходимость различать область как объект пред-

ставления, с которым работает пользователь, и область как часть экрана обу-

словлена тем, что на уровне пользовательского представления существуют

понятия непрерывной кривой, замкнутости, тогда как экранное представле-

642

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

ние — это просто набор точек растра, называемых пикселями, которые раз-

личаются местоположением на экране и цветом.

Экранная область представляет собой связную группу пикселей, т. е. та-

кую, в которой между любыми двумя пикселями можно найти путь, целиком

лежащий в данной области. Соответственно, путь — последовательность

пикселей π

, таких, что π

и π

i+1

— соседние. Области выделяются либо об-

щим цветом своих пикселей, и тогда они называются внутренне определен-

ными, либо цветом границы — линии, составленной из одноцветных сосед-

них пикселей, и тогда они называются гранично определенными. Чтобы эти

определения стали корректными, необходимо указать, как понимается тер-

мин “соседние пиксели”. Различаются 4-связное соседство и 8-связное со-

седство. В первом случае соседними считаются такие пиксели, у которых

либо горизонтальная, либо вертикальная координата отличаются на едини-

цу, во втором — такие, у которых обе координаты различаются не более чем

на 1 (допускается диагональное соседство).

В условиях приведенных определений задача закраски области ставит-

ся следующим образом. Дана замкнутая область и известны координаты ка-

кого-либо ее пикселя. Требуется, чтобы все пиксели области и только они

оказались закрашены одним цветом. Дополнительным условием для данной

задачи является то, что не делается никаких предположений относительно

формы закрашиваемой области.

Стратегия закраски внутренне определенной области,которую можно пред-

ложить для решения задачи, заключается в следующем. Для каждого пиксе-

ля, начиная с известного, проверяется его цвет. Если цвет старый, он заменя-

ется на новый и делается попытка запустить этот алгоритм рекурсивно для

каждого из соседей. Для гранично определенных областей выбор этих же

действий осуществляется по результату проверки несовпадения цвета пик-

селя с граничным цветом, дополненному отказом от перехода к соседу, если

очередной пиксель оказался уже перекрашенным. Понятно, что запуск алго-

ритма для соседей нужно осуществлять четыре раза в случае 4-связного и

восемь раз для 8-связного соседства.

Ниже приводится процедура закраски внутренне определенной области

при 4-связном соседстве. Остальные варианты предлагается запрограмми-

ровать читателю самостоятельно в качестве упражнения. Чтобы не привязы-

ваться к какой-либо графической библиотеке, в представленном алгоритме

вместо конкретных функции выявления и процедуры задания цвета пикселя

11.2. ЗАКРАШИВАНИЕ ЗАМКНУТЫХ ОБЛАСТЕЙ

643

указываются условные

имена:

ЧитатьЦветПикселя

ПисатьЦветПикселя

При использовании приводимой процедуры в конкретных условиях необхо-

димо,во-первых,позаботиться о подключении соответствующей библиотеки

к программе, во-вторых, заменить эти имена.

{ Pascal }

procedure FloodFill4(x,y, {

координаты внутренней точки

}

OldColor, {

цвет области до закраски

}

NewColor {

требуемый цвет области

}

: Integer );

begin

if ЧитатьЦветПикселя ( x, y ) = OldColor

then begin

ПисатьЦветПикселя ( x, y, NewColor );

{

изменение цвета текущего пикселя

}

FloodFill4 ( x, y - 1, OldColor, NewColor );

{

переход к верхнему соседу

}

FloodFill4 ( x, y + 1, OldColor, NewColor );

{

переход к нижнему соседу

}

FloodFill4 ( x - 1, y, OldColor, NewColor );

{

переход к левому соседу

}

FloodFill4 ( x + 1, y, OldColor, NewColor );

{

переход к правому соседу

}

end

end;

/* C */

void FloodFiLL4 (

int x, y, //координаты внутренней точки

OldColor, //цвет области до закраски

NewColor ) //требуемый цвет области

{

if (ЧитатьЦветПикселя (x,y) == OldColor) {

ПисатьЦветПикселя (x,y,NewColor);

FloodFiLL4 ( x, y-1, OldColor, NewColor);

//переход к верхнему соседу

Чтобы подчеркнуть их условность, они записаны на русском языке.

644

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

FloodFiLL4 ( x, y+1, OldColor, NewColor);

//переход к нижнему соседу

FloodFiLL4 ( x-1, y, OldColor, NewColor);

//переход к левому соседу

FloodFiLL4 ( x+1, y, OldColor, NewColor);

//переход к правому соседу

}

Процедура

FloodFill4

достаточно проста и будет часто (но не всегда, см.

упр. 1 ) работать правильно. Однако, хорошо ли она работает? Ответ на этот

вопрос весьма поучителен. При вызове ее для областей, содержащих значи-

тельное количество точек, расположенных по горизонталям и вертикалям,

FloodFill4

будет вызывать себя рекурсивно столько раз, сколько точек лежит

правее, левее, выше и ниже от текущей. К примеру, если правее текущей вну-

тренней точки в области находится 500 точек, то глубина рекурсии, появляю-

щейся только за счет первого внутреннего вызова процедуры, окажется рав-

ной 500, а значит одновременно будет существовать соответствующее число

экземпляров процедуры (из-за других рекурсивных вызовов это число ока-

жется еще больше).

Если удастся сократить рекурсию, то возможности применения процеду-

ры возрастут за счет снижения требований к памяти. Такое сокращение воз-

можно. Достаточно заметить, например, что для одного из направлений мож-

но заменить два рекурсивных вызова (вверх и вниз или влево и вправо) на два

цикла заполнения новым цветом соответствующей полосы области. При та-

кой замене нужно еще позаботиться о переходах к соседям по другому напра-

влению. Это можно сделать разными путями, но, вообще говоря, для продол-

жения процесса без запоминания в стеке или рекурсии точек-соседей полосы

(что, как уже говорилось, одно и то же) здесь не обойтись, что видно, в част-

ности, из рисунка 11.2а. Если первой внутренней точкой будет указана точка

, направление циклов горизонтальное, а после заполнения полосы в каче-

стве соседей для перехода к следующей полосе выбираются только верхние и

нижние соседи точки

, то верхние треугольники области, отделенные гори-

зонтальными штриховыми линиями, окажутся не закрашенными. Напротив,

для областей другой формы такой путь вполне правомерен (см. рис.11.2б), но

это уже нарушение условия задачи. Читателю предлагается самостоятельно

выяснить вопрос о том, когда можно, а когда нельзя ограничиваться выбором

соседей для продолжения процесса только теми точками, которые окружают