Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

11.3. ПЕРЕБОРНЫЕ АЛГОРИТМЫ И РЕКУРСИЯ

655

2 1

2 2

При обратном порядке некоторые кортежи пропадают, другие — повто-

ряются:

2 1

2 2

2 1

2 2

Причина тому понятна: направления упорядоченности не независимы!

Из приведенной программы видно, что второй рекурсивный вызов можно

преобразовать в цикл. И тогда тело процедуры превращается в:

for k := k to N do

begin

V [Ie] := k;

Handle ( V, Ie );

if Ie < N then SelectF( Ie + 1, 1 );

{ if k < N then SelectF( Ie, k + 1 );

— Этот оператор исчезает!

}

end;

К сожалению, небольшое повышение эффективности, которое достига-

ется при такой модификации, снижает наглядность программы: вместе со

вторым рекурсивным вызовом исчезает явно показанное в прежнем тексте

представление о принятом упорядочивании. Это следствие плохой совме-

стимости рекурсий и циклов! Таким образом, данную модификацию мож-

но рекомендавать лишь в тех случаях, когда требуется особая забота об эф-

фективности. Программа 11.3.3 легко может быть преобразована так, чтобы

в результирующих кортежах не появлялись повторяющиеся элементы. Для

этого в нее можно встроить фильтрацию: проверку повторения элемента, ко-

торая будет экранировать присваивание значения

элементу массива

V[Ie]

первый рекурсивный вызов. В

Pascal

’е это достигается с помощью исполь-

зования множества задействованных индексов:

var Ma: set of 1..N;

В результате получается программа 11.3.4.

656

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

Программа 11.3.4

procedure SelectF1( Ie, k : Integer);

begin

if not (k in Ma) then

begin

Ma := Ma + [k];

V [Ie] := k;

Handle ( V, Ie );

if Ie < N then SelectF( Ie + 1, 1 );

Ma := Ma - [k];

end

if k < N then SelectF( Ie, k + 1 );

end;

Проверка, добавление и удаление элемента множества — быстрые операции

при представлении малых множеств (см. п. 9.3.5), принятом в языке

Pascal

Поэтому получается практически чистый выигрыш в эффективности, и во

многих случаях такое прямое преобразование можно рекомендавать. Если

это не так, то требуется более точно (или порою более грубо, но более про-

сто; необходимо соблюдение баланса между сложностью проверки и слож-

ностью повторных вызовов) определить порядок кортежей, не имеющих по-

вторений. Использование множеств может быть рекомендовано для решения

еще одной переборной задачи, подобной только что рассмотренной: для по-

строения множеств неповторяющихся индексов (упражнение 3).

Все приведенные решения (а также другие решения, оставленные для

самостоятельного рассмотрения) демонстрируют ситуацию, в которой кон-

тексты рекурсий содержат существенную долю вычисляемых результатов.

Именно здесь обычно хорошо работает метод перебора/генерации. В сущно-

сти он представляет собой неявное задание отношения полного порядка на

данных, который согласован с естественным частичным порядком. То, что

такое доопределение чаще всего не является однозначным, понятно. Резуль-

таты решения, а также его эффективность обычно существенно зависят от

того, как именно произведено доопределение порядка.

Представленные программы корректны с точки зрения конечности вычи-

слений. Однако их анализ показывает, что все они не являются сильно кор-

ректными,и, соотвественно,вызывают повторный счет. Это хорошо видно из

схемы на рис. 11.4: окончания кортежей для разных значений

-того элемен-

та оказываются одинаковыми. Для данной задачи повторный счет не очень

11.3. ПЕРЕБОРНЫЕ АЛГОРИТМЫ И РЕКУРСИЯ

657

велик, но в других случаях он может оказаться значительным. В связи с этим

мы покажем метод, с помощью которого можно подменять повторный счет

запоминанием результатов. Суть метода в переходе к рекурсивным струк-

турам данных, которые естественно сочетаются с рекурсивными методами

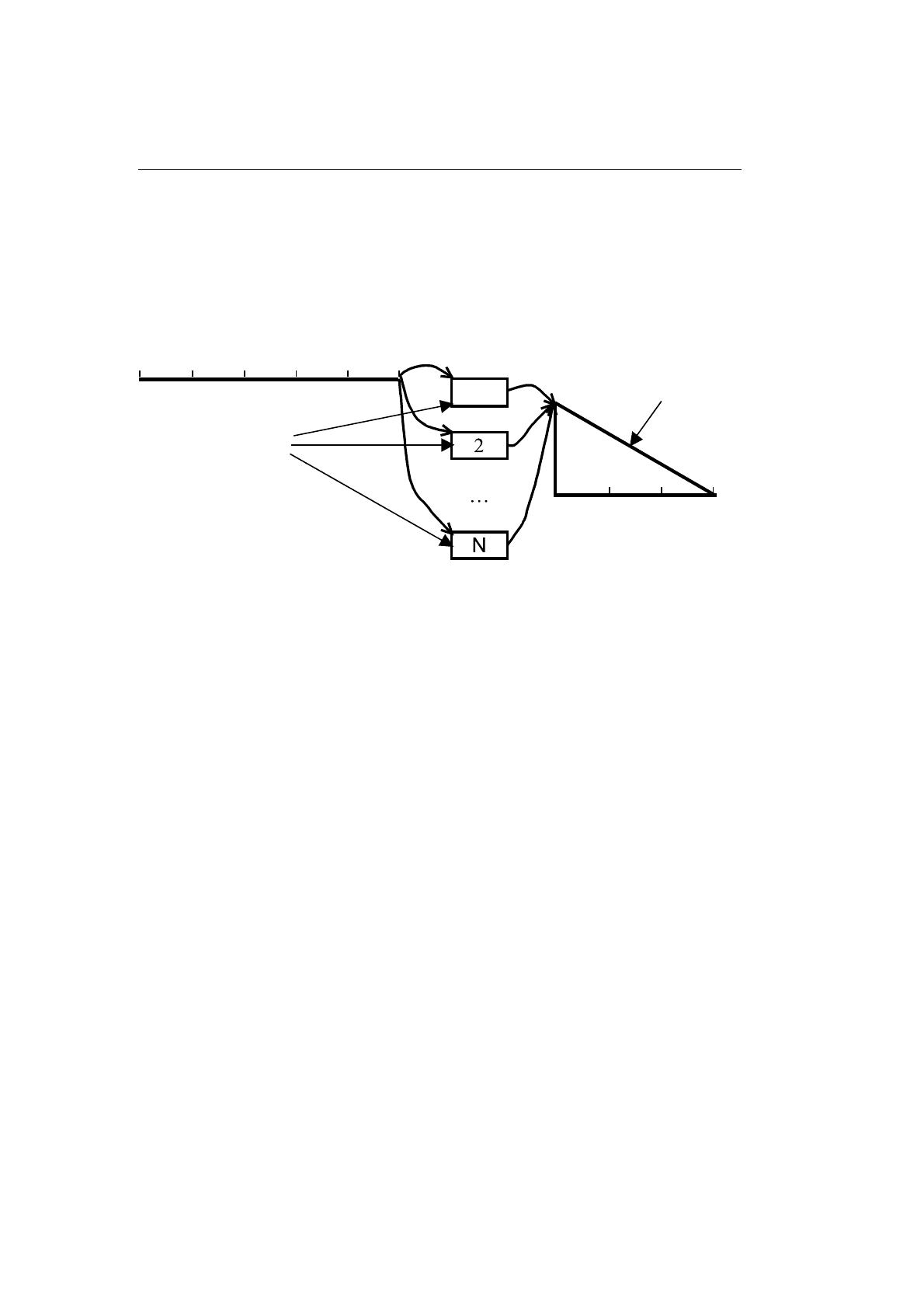
в программировании, а возможность его применения показывает схема на

рис. 11.5, на которой специальными стрелками выделены требуемые связи

Начало

ie-

ый элемент

Общие

окончания

Рис. 11.5. Схема упорядочивания с общими окончаниями кортежей

между составляющими разбиения данных для обсуждаемой задачи.

Программная структура, которая в состоянии обеспечить такие связи —

список, который заменяет массив

(точнее, содержимое этого массива, ме-

няющееся в динамике вычислений). Для перехода от массива к списку нуж-

но пополнить общий контекст программы описаниями типов, определяющих

новую структуру данных:

type PL =^TL;

TL = record inf : Integer;

down, right : PL;

end;

где

inf

— поле для размещения индекса, а

down

right

— поля ссылок на

следующий элемент в вертикальном и горизонтальном направлениях. Пере-

менная, которая будет указывать на список в целом, описывается как:

var Sta : PL;

В новой программе у рекурсивной процедуры

SelectF2

появляется допол-

нительный параметр

, который показывает номер в горизонтальном напра-

влении (ранее он был бы излишним из-за его совпадения с индексом

). В

658

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

алгоритме процедуры вместо присваивания

элементу массива генерирует-

ся новый элемент списка. Первый рекурсивный вызов аналогичен такому же

вызову в прежней программе. Если мы переделаем и второй рекурсивный вы-

зов в подобной манере, то получится решение, отличие которого от

SelectF

будет лишь в том, что следы вычисления кортежей сохраняться в списке.

Для исключения повторного счета вместо этого надо встроить генерацию се-

рии элементов вертикального направления с общей ссылкой на

Окончание

В этом построении неизбежно теряется одно качество прежнего решения:

теперь нельзя совместить обработку (вывод) с формированием списка. Это

вполне понятно, поскольку дополнительный просмотр только что построен-

ных элементов вертикального направления с нужными для обработки про-

смотрами по горизонтальному направлению лишает всех преимуществ ре-

шение о слиянии

Окончаний

. Следующая программа реализует процедуру

SelectF2

, обладающую указанными свойствами.

Программа 11.3.5

procedure SelectF2 ( var Ie : PL; co, k : Integer );

var Cr, Nx : PL;

begin

new (Ie);

Cr := Ie;

with Ie^do

begin inf := k;

down := nil;

right:= nil;

end;

if co < N then SelectF2 ( Cr^.left, co + 1, 1 );

while k < N do

begin k := k + 1;

new (Nx);

Cr^.down := Nx;

Nx^.inf := k;

Nx^.right:= Cr^.right;

Nx^.down := nil;

Cr := Nx;

end;

11.3. ПЕРЕБОРНЫЕ АЛГОРИТМЫ И РЕКУРСИЯ

659

Вызов процедуры

SelectF2(Sta,1,1)

для фиксированного

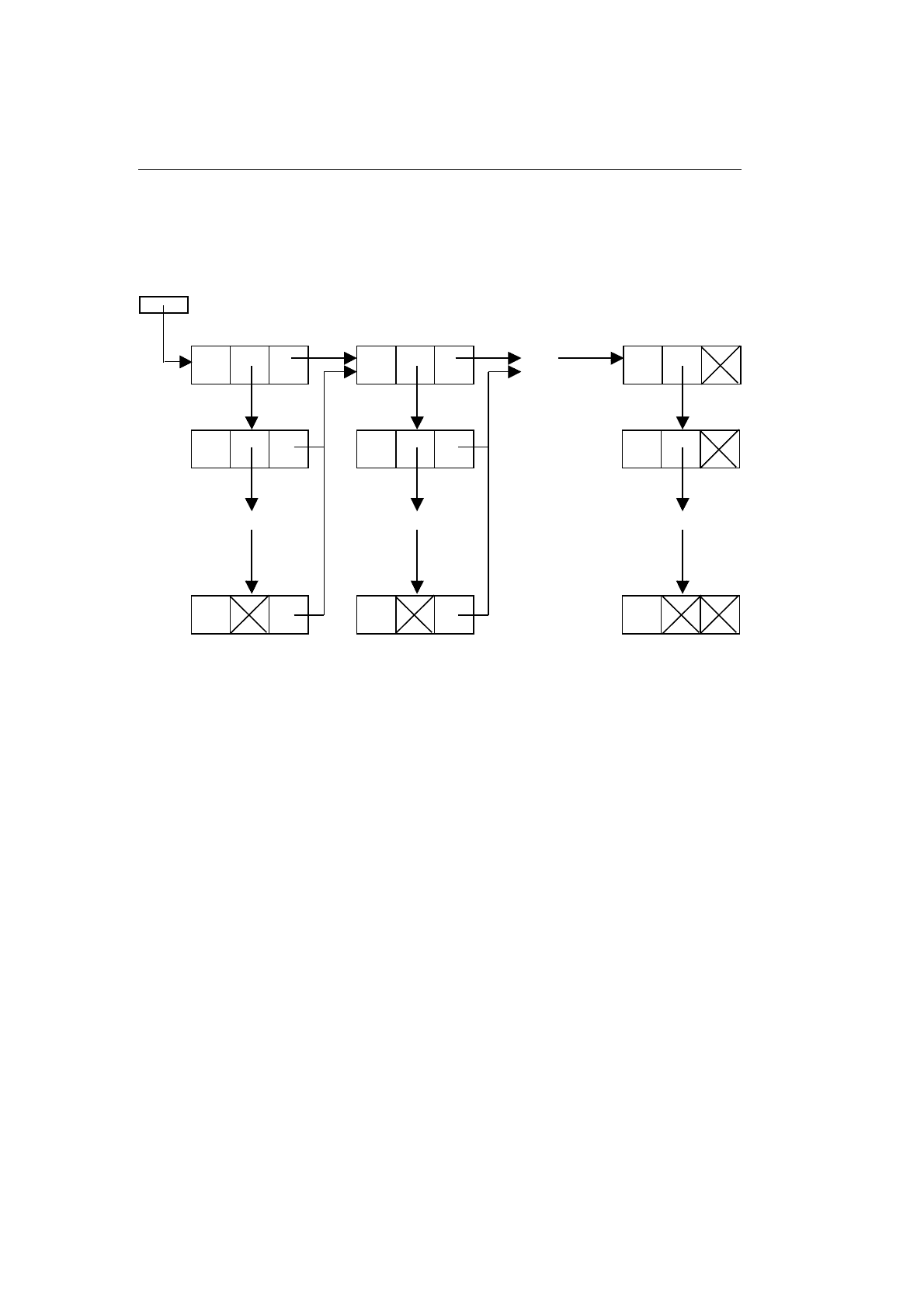
приводит к по-

строению графа, который представлен списком, изображенном на рис. 11.6.

Искомые кортежи строятся при прохождении всех маршрутов, начинающих-

Sta

inf

down

right

1 1 1

…

Рис. 11.6. Граф решений, представленный списком

ся в вершине, на которую указывает

Sta

. Построение кортежа сводится к

выписыванию последовательности пометок вершин графа (поля

inf

) при их

посещении согласно следующему правилу: из всех вершин вертикального

направления перемещения пометка берется только у последней из них. По-

строение всех кортежей может рассматриваться как самостоятельная задача

отслеживания нужных маршрутов без повторений. Возможно ее решение ре-

курсивным методом.При разработке соответствующей программы (это пред-

лагается выполнить самостоятельно) целесообразно не ограничиваться гра-

фами, которые получаются при выполнении процедуры

SelectF2

. Решая за-

дачу для общего случая, мы не только расширяем сферу ее применения (в

частности, должно получиться так, что она будет работать и тогда, когда

склейка окончаний не предусматривается, можно предусмотреть фильтра-

цию решений и т.д.),но и получаем универсальный подход для оперирования

660

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

с графами.

Структура получившегося графа решений вполне регулярна, и можно го-

ворить о построении ее иными методами, нежели те, что были применены

выше. Разумеется, это можно (и нужно!) было выяснить на этапе анализа

задачи, который устанавливает принимаемый метод решения. Но здесь хо-

телось бы подчеркнуть другое. Если сравнить различные решения задачи с

точки зрения того, как вовлекаются данные в вычисления, то становится яс-

но, что структура графа отражает именно эти потоки данных, т. е. фиксирует

в себе все допустимые с точки зрения задействованных алгоритмов порядки

доступа к данным.

Каждый из путей из начальной вершины графа соответствует одному из

искомых решений. Ацикличность построенного графа позволяет при постро-

ении решений не заботиться о контроле длин проходимых путей. Если отка-

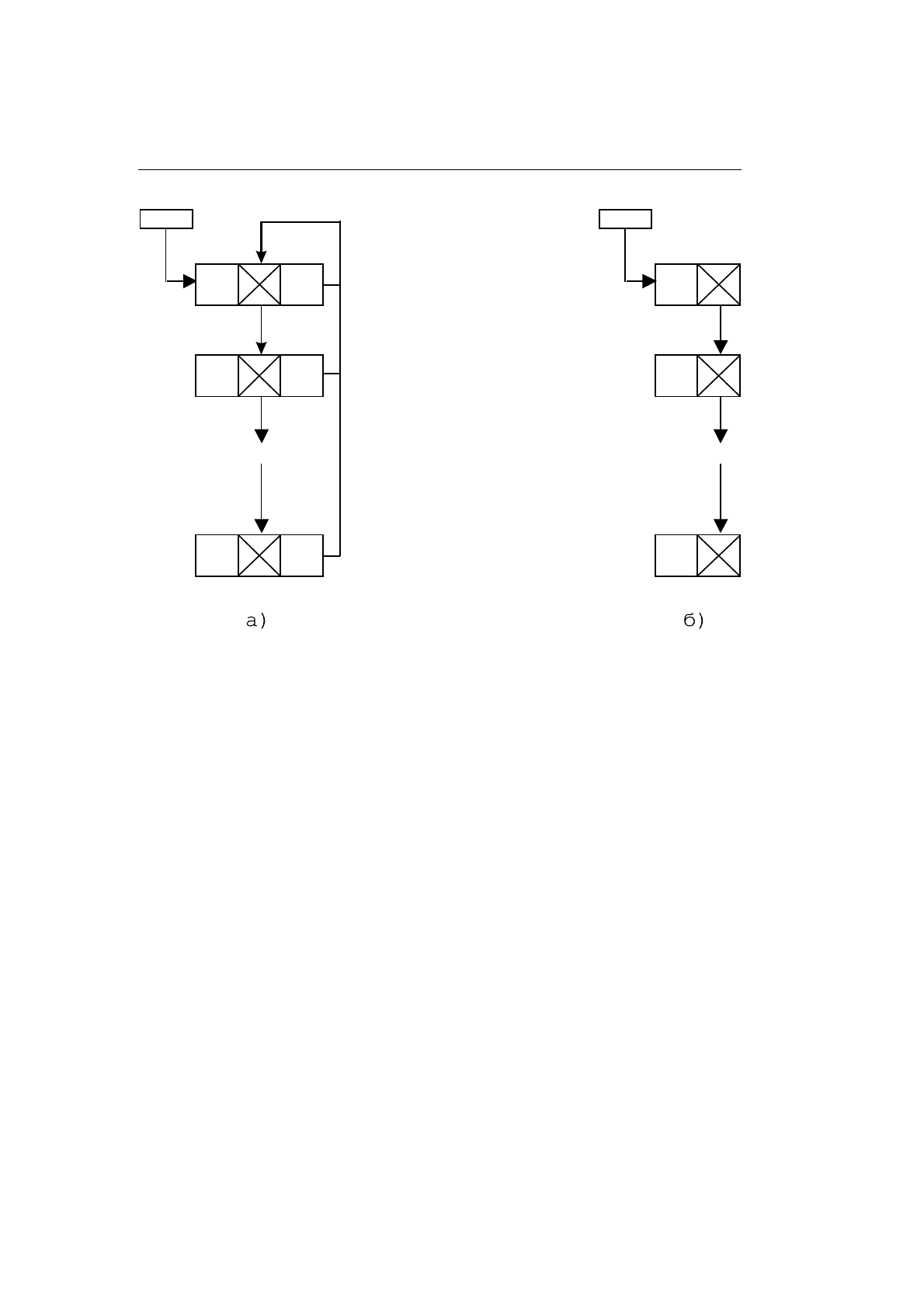
заться от использования этого свойства, то можно еще раз произвести склей-

ку графа по вертикальному направлению (см. рис. 11.7а). Поиск решений для

нового графа может осуществляться той же программой, которая применима

для графов обоих прежних видов (без учета и с учетом совпадений оконча-

ний), если только она контролирует длины проходимых путей. Это принци-

пиально, т. к. новый граф перестает быть ациклическим.

В списочном представлении нового графа оказалось, что все ссылки на-

право (поле

right

) имеют одно и то же значение. Зачем же тогда хранить их

в каждом элементе? Очевидный ответ на этот вопрос приводит к тому, что

требуемую списочную структуру целесообразно преобразовать в простой по-

следовательный список (см.рис. 11.7б).Прежняя программа для его обработ-

ки не годится, но из нее легко (даже механически!) можно построить новую

программу, соответствующую измененной структуре данных.

Содержимое элементов этого списка для решаемой задачи соответствует

следованию чисел отрезка натурального ряда, записанного в поле

Inf

. Поэто-

му сам такой список становится избыточным: вместо его просмотра более

эффективно реализовать непосредственное оперирования с этим отрезком.

А это возврат к тому, что было реализовано в первом или втором решении,

которые вовсе не используют граф. Впрочем, теперь они оказались упрятан-

ными в программе обработки (

Handle

Круг замкнулся. Приведенными построениями мы показали, что для ре-

В данном случае это слово практически является термином: поток данных задает частич-

ный порядок на них, фиксирующий разрешение доступа к данным: чтодбы данное

стало

доступным, нужно обработать все предшествующие ему.

11.4. ЛАБИРИНТ

661

Sta Sta’

…

Рис. 11.7.Два вида графа решений: (а)— список со склеенными вертикалями

и (б) — список-последовательность.

шаемой задачи переход от рекурсивной программы к рекурсивным данным

не дает преимуществ. Но не следует по этой причине считать наши постро-

ения излишними: в других случаях подобный переход может быть целесо-

образным во многих отношениях, и во всяком случае его нужно запомнить

как общий прием программирования.

§ 11.4. ЛАБИРИНТ

В настоящем параграфе приводится иллюстрация метода перебора/генерации

вариантов с возвратами, когда требуется найти не все, а одно из возможных

решений. В качестве области применения метода обсуждается разработка ал-

горитмов блуждания по лабиринту, т. е. нахождения путей в лабиринте из

заданной точки. В учебном плане задача блуждания по лабиринту удобна в

нескольких отношениях. Во-первых, она является весьма характерной пере-

662

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

борной задачей, требующей просмотра вариантов с возвратами. Во-вторых, в

ней легко усмотреть связь с задачей закраски области (§ 11.2). Попытка при-

менить уже наработанный подход к решению оказывается поучительной. В-

третьих, на примере данной задачи можно проследить один важный техно-

логический подход к решению программистских задач, связанный с разбие-

нием задачи на подзадачи.

11.4.1. Блуждание по лабиринту и закраска области

Задача закраски области может быть достаточно просто переформулиро-

вана для случая блуждания по лабиринту, когда требуется найти все точки

области, достижимые из заданной точки. В такой постановке новая задача

допускает решение, ничем не отличающееся от решения задачи о закраске.

В самом деле, возможность перехода из одной точки лабиринта в другую пол-

ностью соответствует понятию соседства точек,и как следствие,закраску со-

седней точки можно трактовать как переход в нее, а осуществление закраски

всей области — как отметку всех последовательно достижимых точек. Од-

нако если слегка изменить постановку задачи блуждания, потребовав опре-

делить не существование пути, а сам путь из одной точки в другую, то об-

наружится, что алгоритм закраски области потребует корректировки. Кстати

сказать, новая постановка более естественна для задачи блуждания.

Почему для нахождения пути из одной точки в другую подход, предста-

вленный в предыдущем разделе, не годится? Дело в том, что он не фиксирует

последовательности перемещений по точкам, более того, для закраски прин-

ципиально, что одна и та же точка посещается не один раз, а столько, сколько

нужно для закраски всех соседствующих с ней точек. При решении новой же

задачи нужно научиться отвергать (исключать из рассмотрения) точки, пере-

ходы из которых ведут в тупики (не только зацикливание). В прежней задаче

отвергались лишь граничные точки, что сохраняется и для задачи блужда-

ния, и те точки, соседи которых лежат на границе области или уже закраше-

ны. Иными словами, определить, нужна ли конкретная точка для продолже-

ния процесса (для рекурсивного вызова процедуры), можно было локально.

Теперь же, составляя последовательность точек (последовательности, если

требуется найти разные пути), представляющей искомый путь (пути), отвер-

гать точки нужно после исследования, ведет ли из нее путь в точку назначе-

ния. Весьма поучительно попробовать попытаться воспользоваться прежним

алгоритмом для решения данной задачи непосредственно и увидеть его де-

фекты.

Есть еще одна особенность новой задачи, важная уже на уровне уточ-

11.4. ЛАБИРИНТ

663

нения постановки: при блуждании по лабиринту для каждой точки всегда

можно выделить множество очевидно достижимых из нее точек. В него, к

примеру, попадают все соседние неграничные точки, весь луч из данной точ-

ки до пересечения его с границей (интуитивное представление видимости).

Поэтому можно ввести понятие множества точек, очевидно достижимых из

данной. Очевидно достижимые точки определять можно по-разному, но при

выполнении одного условия: для поиска пути в лабиринте в качестве началь-

ной (конечной) точки выбор какой-либо из них в множестве очевидно дости-

жимых точек безразличен.

Иными словами, для блуждания в лабиринте все множества взаимно оче-

видно достижимых точек группируются в классы эквивалентности, и вместо

точечного пространства, аналогичного области закраски, в задачах о лаби-

ринте нужно оперировать с набором классов эквивалентности. Для опреде-

ленности будем называть такие классы комнатами, искусственно устанавли-

вая границы комнат как окончания очевидно существующего перехода меж-

ду точками. Эти границы либо совпадают с фактическими границами лаби-

ринтного пространства, которые в дальнейшем называются стенами, либо

добавлены для разграничения комнат, связанных возможным переходом, —

двери. В результате в качестве начала и конца искомого пути указываются не

точки, а комнаты, а сам путь рассматривается как последовательность ком-

нат.

Таким образом, задача о лабиринте становится дискретной. В ней можно

выделить в ней два независимых аспекта:

• графическое отображение лабиринта и

• нахождение пути в нем.

Следует заметить, что и при решении задачи раскраски фактически был

осуществлен переход к дискретной постановке: непрерывность границ обла-

сти рассматривалась как наличие среди соседей каждой граничной точки

других граничных точек. В свою очередь, именно это позволило разрабо-

тать универсальный алгоритм, не зависящий от (аналитического) вида гра-

ниц области закраски (правда, у этого алгоритма есть недостаток: он очень

чувствителен к непрерывности отображения границы области на экране, т. е.

неустойчив к пропуску граничных пикселей). В задаче раскраски не было не-

обходимости выделять аспект графического отображения, она формулирует-

ся для заданной, т. е. уже изображенной области. Таким образом, дискретное

представление области закраски остается реализационным.

664

ГЛАВА 11. МЕТОДЫ, ОСНОВАННЫЕ НА РЕКУРСИИ

Для блуждания по лабиринту ситуация иная. Задача поиска пути может

ставиться для изображенного лабиринта, но, тем не менее, и в этом случае

подразумевается, что ее решение должно формулироваться как последова-

тельность комнат, дверей, а не на уровне точечного представления. Кроме

того, естественно предполагать, что решение, полученное для одного лаби-

ринта, окажется тем же самым для любого другого, подобного ему лабиринта

(вопросы, связанные с подобием, обсуждаются в следующем параграфе).

11.4.2. Абстрактное и конкретное представления данных

Прежде всего, разберемся с тем, что означает абстрактное представление

данных в программировании.

Предельно абстрактным представлением данных (пока мы не имеем дело

со значениями высших типов) можно считать алгебраическую систему. Она

состоит из совокупности непустых множеств (носителей системы), которые

соответствуют базовым типам данных рассматриваемой структуры, совокуп-

ности функций и предикатов над этими носителями, часть из которых станет

методами создаваемых программных объектов

, а часть так и останется при-

зраками.

Соответственно, данные считаются изоморфными, если изоморфны со-

ответствующие им алгебраические системы.

Но это предельно абстрактное математическое представление данных не-

достаточно для программирования. Подобно тому, как было введено понятие

абстрактного синтаксиса программы, можно выделить и абстрактное про-

граммное представление, фиксирующее те программные сущности, которые

обязаны быть представлены для реализации нужных нам алгоритмов над рас-

сматриваемой структурой данных. Некоторым (весьма полезным, но недо-

статочным!) приближением к абстрактному представлению данных в про-

граммировании служат абстрактные классы в ООП (см. стр. 717).

В абстрактном представлении мы фиксируем лишь необходимые для ре-

ализуемого алгоритма особенности структур данных и методов. В частно-

сти, можно практически полностью игнорировать вопросы представления

информации при вводе и выводе, если данные вопросы не являются критиче-

скими для алгоритма. Но даже если эти вопросы оказались для нас критиче-

Здесь слово метод полностью согласуется с тем значением, которое ему в идеале желают

придать в объектно-ориентированном программировании, но никак не привязано к тому,

является ли конкретная реализация объектной.