Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

10.3. СИНТАКСИЧЕСКИЕ ТАБЛИЦЫ

605

А можно ли с помощью данного метода убить сразу двух зайцев? Ока-

зывается, это можно сделать, если вспомнить, что задача анализа вовсе не

требует восстановления дерева разбора строки. Это означает, что можно ана-

лизировать входной поток в соответствии с грамматикой, которая отличается

от заданной изначально. Но при замене грамматики должны быть выполнены

два условия:

• новая грамматика должна быть эквивалентна исходной (порождает тот

же язык);

• действия,которые надо выполнять после анализа, и которые заданы как

функции от исходной грамматики, должны быть согласованы с новой

грамматикой.

Если первое условие ставит чисто формальные рамки (к тому же не очень

строгие, т. к. вполне допустимо выбрать новую грамматику так, чтобы поро-

ждаемый язык включал исходный, и применить фильтрацию на уровне дей-

ствий), то второе может вызывать затруднения. Но в нашем случае это не так.

Вместо (10.3) можно воспользоваться для выражения и множителя следую-

щими правилами:

<выражение> ::= <множитель> [ “+” <множитель> |

“−” <множитель>]*

<множитель> ::= <терм> [ “*” <терм> |“/” <терм> ]*

(10.3)

которые, очевидно, порождают тот же язык.

В качестве второго условия в данном обсуждении используется согласо-

вание грамматики с порядком вычислений. В реализующей программе это

легко достигается, поскольку оперирование полностью сосредоточено в дей-

ствиях каждого из автоматов (см. таблицы 10.7 и 10.8). В данном случае нет

никаких противоречий в том, чтобы разработчики сами выбирали порядок

действий.

В последних двух таблицах прямая рекурсия удалена. Вместо нее исполь-

зованы циклы. Хорошо это или нет? Хорошо с точки зрения эффективности и

возможности задавать нужный порядок. Плохо, если это ведет к нарушению

понимаемости. В данном случае это не так, но, вообще говоря, преобразова-

ние грамматики часто отрицательно сказывается на наглядности программы,

По вычислительной мощности синтаксические таблицы (даже без строк с

E-переходами и действий) равносильны машине Тьюринга. Но нерегламен-

тированное их использование может вызвать значительные трудности при

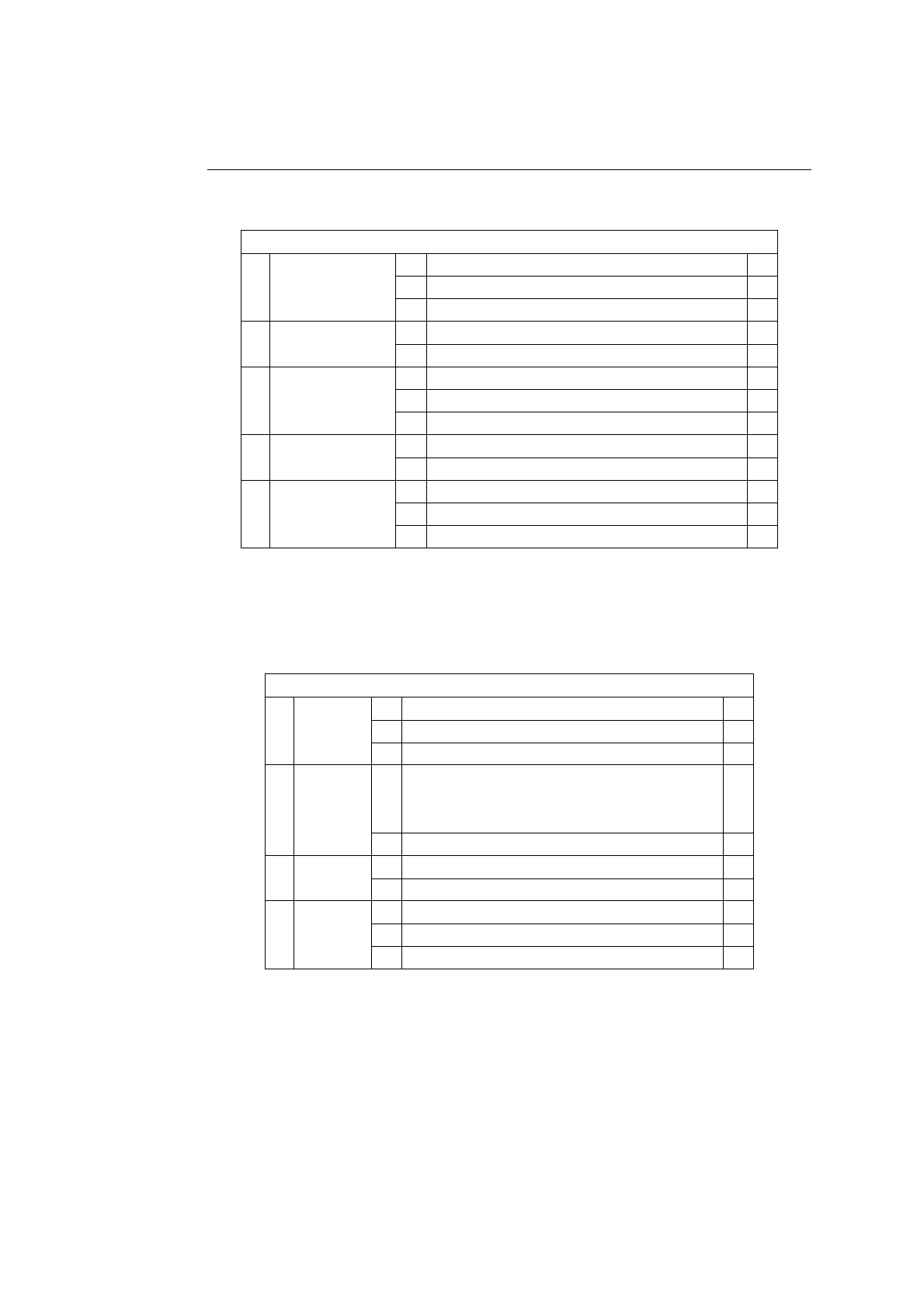
606

ГЛАВА 10. МЕТОДЫ ПРОГРАММИРОВАНИЯ ОТ СОСТОЯНИЙ

<выражение>

<множитель

> T

F /*

распознано, что выражения нет

*/ F

E /*

ошибка в множителе

*/ E

2 “+” T

F 1

<множитель

> T /*

зацикливание

*/ 2

F /*

после “+” нет множителя

*/ E

E /*

ошибка в множителе

*/ E

1 “-” T

F /*

распознано выражение

*/ T

<множитель

> T 2

F /*

после “-” нет множителя

*/ E

E /*

ошибка в множителе

*/ E

Таблица 10.7. Модифицированная диаграмма для выражения

<множитель> /*

все аналогично

<терм

> T

F F

E E

2 “*” T /*

пример того, что можно объединить

два вызова понятия (ср. <выражение>)

F 1

1 “/” T

F T

0 <терм> T 2

F E

E E

Таблица 10.8. Модифицированная диаграмма для множителя

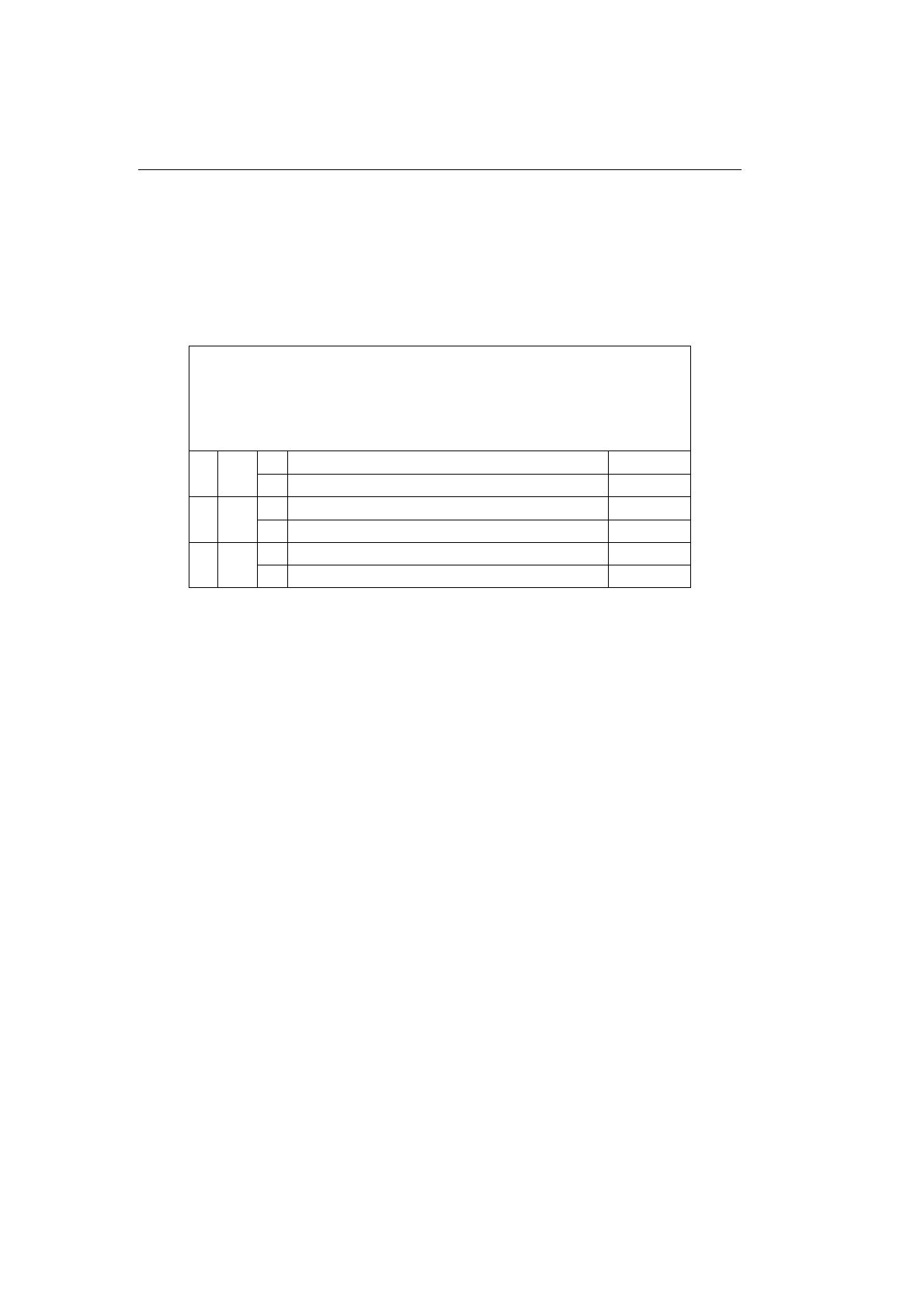
10.3. СИНТАКСИЧЕСКИЕ ТАБЛИЦЫ

607

понимании программ. В этой связи стоит посмотреть, как распознается не

контекстно-свободный язык

| 0 6 n}

с помощью синтаксических таблиц,снабжаемых соответствующими действи-

ями (таблица 10.9).

int Parser_aNbNcN ();

/* возвращает -1, если строка не принадлежит

| 0 6

,и N,если она содержит по Nбукв a,bи cв нужном порядке

int I = 0; J;

1 “a” T I++; 1

F J = I;

2 “b” T J--; 2

F if (J != 0) return ( -1 );

3 “c” T J++; 3

F if (I != J) return ( -1 );else return ( I );

Таблица 10.9. Распознаватель не контекстно-свободного языка

И последнее замечание. Синтаксические таблицы не обязательно связы-

вать с задачей синтаксического анализа контекстно-свободных грамматик.

Ничто не препятствует использованию их для решения по видимости со-

вершенно других задач. Если удается представить в табличном виде неко-

торой процесс, то, как правило, его реализация облегчается даже тогда, ко-

гда приходится транслировать таблицу вручную. По существу, таблица —

это описание некоего автомата, она строится, когда такой автомат удобен для

данного вида обработки. Например, последовательности корректных упра-

вляющих воздействий часто описываются структурами, изоморфными кон-

текстно-свободным грамматикам. При этом не обязательно связывать работу

такой управляющей таблицы с вызовами процедур, она может быть, напри-

мер, инструментом для построения системы типов данных или аппаратной

реализации. В этом случае методы, разработанные в программировании от

состояний, могут быть перенесены на области, далекие от конечных автома-

тов.

10.3.5. Построение графа состояний

608

ГЛАВА 10. МЕТОДЫ ПРОГРАММИРОВАНИЯ ОТ СОСТОЯНИЙ

В §10.2 и 10.3 мы обсуждали возможности организации таблиц как сред-

ства задания конечного автомата и одного из возможных его расширений. Это

расширение, использованное для решения задачи нисходящего контекстно-

свободного анализа языка, значимо как само по себе, так и в качестве демон-

страции метода конечных автоматов. Продолжая обсуждение метода, стоит

сравнить два представленных выше вида таблиц:

1. Для конечного автомата строится одна таблица на все состояния, тогда

как для синтаксического анализатора составляются отдельные табли-

цы для каждого понятия;

2. В таблице конечного автомата не указываются исходы проверки усло-

вий переходов, и, следовательно, неявно для реализации предписыва-

ется использовать выбор, тогда как в синтаксическом анализаторе при-

меняются указание исходов проверок и явное задание переходов к сле-

дующему элементу, что ориентирует реализацию на распознавание по-

следовательности составляющих.

3. В таблице конечного автомата нет иных меток перехода, кроме как на-

именований состояний (иное решение потребовало бы фиксации по-

рядка проверки условий переходов). Следовательно, в таблице конеч-

ного автомата нет возможности организовать иной цикл, кроме того,

который предписывается самой моделью вычислений.

4. В таблице конечного автомата возможны выделенные элементы —усло-

вия переходов, отвечающие за работу в случаях, когда не требуется чте-

ние из входного потока. Эта задача в синтаксических таблицах не воз-

никает, т. к. в выбранном методе анализа путем проверки первого сим-

вола (лексемы) конструкции выясняется, что конструкция должна быть

распознана полностью.

5. У двух таблично заданных автоматов разная распознающая сила. Син-

таксические таблицы — более мощное средство за счет привлечения

дополнительной (стековой) памяти. Конечный автомат этого не требу-

ет, а потому может и должен реализоваться на традиционной архитек-

туре вычислительного оборудования эффективнее.

В связи с последним замечанием уместно подчеркнуть что, как мы могли

убедиться, разные варианты трансляции таблиц оказываются неравнознач-

ными с точки зрения эффективности. Так, вариант 1, реализующий конечный

10.4. ДИАГРАММЫ СОСТОЯНИЙ И ПЕРЕХОДОВ. ИХ СВЯЗЬ С МАТЕМАТИЧЕСКИМИ МОДЕЛЯМИ

609

автомат с помощью функций-состояний (см. программу 10.2.1), не годится

именно из-за того, что он ориентируется на использование стека, который

является адекватной базовой структурой для синтаксических таблиц.

§ 10.4. ДИАГРАММЫ СОСТОЯНИЙ И ПЕРЕХОДОВ.

ИХ СВЯЗЬ С МАТЕМАТИЧЕСКИМИ МОДЕЛЯМИ

Вначале сделаем несколько методологических замечаний.

Если какие-то понятия образуют систему с достаточно сложной структу-

рой, то необходимо различать четыре вида представления такой системы.

a) визуальное представление системы, которое предназначено для человека;

его можно рассматривать как спецификацию задачи;

b) теоретическое (математическое) представление, которое предназначе-

но для анализа свойств системы и ее преобразований; его можно рассма-

тривать как формализацию задачи;

c) алгоритмическое представление, связывающее визуальное и теоретиче-

ское представление с программой и являющееся спецификацией програм-

мы;

d) программное представление, которое наконец-то предназначено для ис-

полнения некоторого приближения к данной системе на реальном вычи-

слителе.

Рассмотрим требования к различным формам представления.

• к визуальным представлениям: понятность для человека, в том числе,

желательно, и для неспециалиста;

• к математическим представлениям: понятность для специалиста и на-

личие мощной системы преобразований;

• общее требование к первым двум пунктам: статическая проверяемость

свойств;

Таким образом, в принципе математическое представление избыточно, если у нас нет воз-

можности эффективно использовать его для преобразования алгоритма. Но оно зачастую

играет еще и другие роли, одна из которых отмечена в следующем пункте, а вторая — за-

щита принятых решений от неквалифицированной критики и убеждение заказчика и/или

начальника и оппонентов в их обоснованности.

610

ГЛАВА 10. МЕТОДЫ ПРОГРАММИРОВАНИЯ ОТ СОСТОЯНИЙ

• к алгоритмическим представлениям: ясность для программиста;

• к программным представлениям: осуществимость эффективной обра-

ботки;

• общее требование к паре соседних представлений: достаточно простое

(в идеале однозначное) соответствие между ними, позволяющее легко

переходить между уровнями и поддерживать согласованность и аде-

кватность всей системы описаний.

Теперь перейдем к более систематическому рассмотрению тех структур,

которые лежат в основе программирования от состояний. Мы заметили, что

общее визуальное представление алгоритмической спецификации, которая

затем перерабатывается в программу, написанную в стиле от состояний —

граф состояний и переходов.

Определение 10.4.1. Граф состояний и переходов, называемый также диа-

граммой переходов — нагруженный ориентированный граф G. Каждой вер-

шине графа G сопоставлено наименование состояния, а каждой дуге — усло-

вие.

Конец определения 10.4.1.

Примеры таких диаграмм можно посмотреть в предыдущем параграфе.Усло-

вие AB, сопоставленное дуге, ведущей из a в b, содержательно интерпрети-

руется следующим образом. При выполнении AB в состоянии a управление

передается состоянию b (или же в другом смысле осуществляется переход по

данной дуге).

Когда граф состояний и переходов используется для документирования

программы,наименования состояний,как правило,совпадают с именами про-

цедур, выполняющихся в данном состоянии.

Прежде всего, рассмотрим подробнее вопрос, по какой причине в про-

граммистских работах диаграммы переодов и конечные автоматы употре-

бляются почти как синонимы. Вычисления, соответствующие диаграммам

переходов, могут быть представлены циклом, телом которого является по-

следовательность трех действий:

Исполнение процедуры, сопоставленной состоянию;

Проверка условий, сопоставленных выходящим дугам,

выбор дуги, соответствующей истинному условию;

Переход к состоянию, в которое ведет выбранная дуга;

10.4. ДИАГРАММЫ СОСТОЯНИЙ И ПЕРЕХОДОВ. ИХ СВЯЗЬ С МАТЕМАТИЧЕСКИМИ МОДЕЛЯМИ

611

Если отвлечься от конкретных действий, выполняемых в состояниях (при-

рода которых может быть очень сложной), и перейти к схеме программ, то

мы получаем схему Янова (см. § A.3), и, более того, схему Янова частного

вида. Если далее упростить условия на дугах, то мы можем закодировать их

символами алфавита, мощность которого не больше мощности множества

состояний на диаграмме. При этом коды всех дуг, выходящих из данного со-

стояния, будут различаться. Далее мы можем построить конечный автомат,

моделирующий поведение схемы Янова в следующем смысле:

1. Состояния автомата обозначаются натуральными числами i и взаимно-

однозначно соответствуют функциональным блокам (действиям) схе-

мы Янова, и, соответственно, состояниям диаграммы переходов;

2. Символы входного алфавита обозначаются теми же натуральными ча-

слами;

3. В программной матрице автомата элемент A

= k тогда и только тогда,

когда в диаграмме переходов дуга, начинающаяся в состоянии, код ко-

торого i, и закодированная буквой j, ведет в состояние, закодированное

числом k.

Для каждого исполнения схемы Янова, соответствующей нашей диаграмме

переходов, существует входная лента построенного нами автомата, порожда-

ющая ту же последовательность состояний.

Таким образом, математический переход от диаграмм состояний к конеч-

ным автоматам весьма прям и весьма груб. Это типичное приближение пер-

вого порядка

. Приближения первого порядка являются легче всего исследу-

емыми математическими моделями систем. Сделанные при их построении

огрубления часто приводят к тому, что, базируясь на таком приближении,

приходят к ложным выводам о поведении системы. Например, приближени-

ем первого порядка функции sin в точке 0 является прямая y = x. Поведение

этой прямой и поведение синуса на достаточно больших отрезках не имеют

ничего общего даже с качественной точки зрения. Такой эффект огрубления

Понятие приближения первого порядка, приближения второго порядка и т. д. появились

при применении разложений функций в ряд Тейлора для получения приближенных реше-

ний систем. В общем случае системного анализа эти понятия служат полезным маяком и

порождают аналогичную, но, конечно, не формализованную и неформализуемую, систему

оценок для нечисленных математических моделей.

612

ГЛАВА 10. МЕТОДЫ ПРОГРАММИРОВАНИЯ ОТ СОСТОЯНИЙ

возникает и в наших системах, формализуемых диаграммами переходов

Тем не менее, как и многие другие математические модели первого порядка,

автоматная аналогия диаграмм переходов дает много полезного для обраще-

ния с диаграммами и получающимися программами, если ее не абсолюти-

зировать. В частности, методы преобразования и оптимизации автоматов ча-

сто могут прямо применяться для преобразования и оптимизации программ,

описанных диаграммами переходов.

Мы уже рассмотрели один случай, когда структура, по виду совершенно

аналогичная диаграммам переходов, на самом деле имеет другую интерпре-

тацию. А именно, это — синтаксические таблицы. В синтаксических табли-

цах на самом деле мы имеем рекурсию, замаскированную тем, что аргумен-

ты рекурсивного обращения к процедурам всегда вычисляются стандартно:

это — текущее подвыражение. Здесь годятся методы преобразования авто-

матов, связанные с экономией состояний, но методы декомпозиции и ком-

позиции уже не идут, поскольку в данном случае автомат на самом деле не

конечный, а магазинный, и прямо представить последовательности его со-

стояний в виде полугруппы не удается.

Это лишь первый из отмеченных нами случаев, когда поверхностные ана-

логии, связанные с совпадением грубейших представлений и (иногда вдоба-

вок еще и) грубейших математических моделей ведут в концептуальные ту-

пики.

§ 10.5. ПРОГРАММНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФА СОСТОЯНИЙ

Отметим, что программные представления графа состояний очень сильно

зависят от динамики данного графа. Стоит выделить четыре подслучая.

1. Состояния и таблица переходов жестко заданы постановкой задачи (на-

пример,такова задача синтаксического анализа).Тогда практически все-

гда лучшее программное представление —

goto

, независимо от разме-

ра таблицы.

2. Состояния и таблица переходов пересматриваются, но фиксированы

между двумя модификациями задачи. Тогда при небольших размерах

таблицы по-прежнему предпочтительней всего реализация через пере-

ходы, а при достаточно больших необходима ее декомпозиция, в связи

Диаграммы переходов можно считать моделями второго порядка. Хотя действия по-преж-

нему остаются неконкретизированными, условия переходов выписываются более детально.

10.5. ПРОГРАММНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФА СОСТОЯНИЙ

613

с чем часто целесообразно представление состояний объектами.

3. Состояния и таблица переходов динамически порождаются перед вы-

полнением данного модуля, и фиксированы в момент его выполнения.

Тогда лучший способ реализации — задание таблицы переходов в ви-

де структуры данных и написание интерпретирующей программы для

таких таблиц.

4. ‘Живая таблица’: модифицируется в ходе исполнения. Пока что дать

методологические советы для таких таблиц мы не можем, хотя очевид-

но, что, несмотря на внешнюю рискованность, такой путь явился бы

чрезвычайно выигрышным для многих систем адаптивного реагирова-

ния.

В контексте этих ситуаций следует рассматривать и работу с табличным пред-

ставлением конечных автоматов, в частности, систему конечных автоматов

как средство расширения их распознающих возможностей. Приведенные вы-

ше примеры ручной трансформации таблиц в программный формат дают

представление о том, какую цель можно ставить, если решать задачу их ав-

томатического перевода на язык программирования, а указанные ситуации

служат ориентиром для выбора между трансляционным и интерпретацион-

ным подходом к реализации. В связи с этим далее мы уточним постановку

задачи перевода для конечного автомата и обозначим варианты ее решения

применительно к конечному автомату, подсчитывающему длины слов. Затем

будет рассмотрена задача,которая по существу является автоматной, но прин-

ципиально не может быть решена с помощью ручного построения таблиц

конечного автомата.

10.5.1. Требования к автоматической трансляции таблиц

Серьезный недостаток предложенного в § 10.2.5 решения задачи автома-

тического преобразования диаграмм конечного автомата в программу свя-

зан с идеей препроцессорного построения, удобного для обработки предста-

вления диаграмм переходов. Игнорирование обратной связи между исход-

ным представлением автомата и его интерпретируемым представлением по-

рождает проблемы. Если не рассматривать развитие программы, то отсле-

живать ее не нужно. Но как только встает вопрос о хотя бы минимальных

переделках, возникает проблема:

614

ГЛАВА 10. МЕТОДЫ ПРОГРАММИРОВАНИЯ ОТ СОСТОЯНИЙ

• внесение изменений в диаграмму не влечет за собой автоматического

изменения внутреннего представления, а возможные нарушения согла-

шений, связанных с исходным решением, могут сделать бессмыслен-

ным переиспользование. Это особенно заметно, если обратить внима-

ние на то, что в результирующей таблице отсутствуют имена состоя-

ний;

• поиск и диагностика ошибок (речь идет не только о синтаксисе) воз-

можны лишь на уровне интерпретируемого представления, что проти-

воречит осмысливанию программы в прежних терминах;

• наличие программы, не зависящей от исходного представления, про-

воцирует на ее модификации, которые не будут перенесены в исходное

представление. В результате концептуальная и реализационная модели

расходятся между собой.

Таким образом, предложенное решение не является технологичным. Оно мо-

жет быть распространено на другие ситуации лишь для очень узкого круга

задач.

Все, сказанное выше, в полной мере может быть отнесено и к синтакси-

ческим таблицам. В обоих случаях задача разработки технологии включает в

себя создание и использование инструментов поддержки всех этапов, из ко-

торых состоит технологическая цепочка оперирования с таблицами. Ключе-

вым моментом является выбор формата представления таблиц, приспосо-

бленный как к ручной, так и к автоматической обработке.

Есть смысл попытаться отыскать универсальное решение. Если плюс к

этому оно будет стандартизовано, то появляется возможность создать техно-

логию. Сегодня предпосылки для такого решения существуют: использова-

ние так называемых языков разметки текстов и, в первую очередь,

XML

10.5.2. Языки разметки и автоматическая трансляция таблиц

При обсуждении Программы 10.2.5 мы указывали, что предложенный

текст является размеченным символами _i, i = 1, . . . , 5. Было показано, как

от размеченного текста переходить к программе на языке

С++

или к интер-

претации таблицы.У такой разметки только один недостаток: она не стандар-

тизована, а потому о распространении далее среды разработчиков системы,

предназначенной для поддержки применения таблиц, говорить не приходит-

ся.