Некипелов А. Становление и функционирование экономических институтов

Подождите немного. Документ загружается.

50 Глава

Экономика «робинзонады»

риод

МЫ

рассматриваем как самостоятельный у но не изолирован-

ный от первого. Стоящая перед Робинзоном задача состоит в том,

чтобы максимизировать общую полезность за два рассматриваемых

периода. Поэтому созданные в первом периоде орудия труда есть

лишь преходящий момент в производстве потребительских благ во

втором периоде и вся их роль в производственном процессе сводит-

ся к повышению производительности труда во втором периоде. Если

же мы рассматриваем второй период изолированно от первого, то

упомянутые орудия труда должны рассматриваться как самостоя-

тельный, дополняющий рабочую силу самого Робинзона, ограни-

ченный фактор производства (этот фактор производства оказывает-

ся в данном случае заданным экзогенно). Соответствующая пробле-

ма будет рассмотрена в следующем параграфе.

Итак, потере в общей величине полезности в первом периоде,

связанной с трудовыми инвестициями, противостоит увеличиваю-

щаяся общая полезность во втором периоде. Рассмотрим теперь

подробнее, что количественно означают эти потери и выигрыши

полезности.

Начнем с первого периода. Время трудовой деятельности те-

перь будет состоять из двух частей: времени труда, нацеленного

на создание потребительских благ (^

Й^

•

х,), и времени трудовых

инвестиций (/). Однако полезность в текущем периоде будет при-

носить лишь первая его часть. Время же трудовых инвестиций

—

это всего лишь параметр, уменьшающий величину «полезно ис-

пользуемого» времени Г. Поэтому в модели максимизации полез-

ности Робинзона применительно к первому периоду трудовые ин-

вестиции /, как и параметры

а^,

не должны быть представлены в

целевой функции:

U=U{x^,...,x,„L),

г=1,...,

п\ (1.30)

при ограничении (условии связи)

1=1

Функция Лагранжа (1.6) будет выглядеть так:

3 = U(x^,...,x^,L)

X'(T-tai'Xi-L-1). (1.31)

i=l

Максимизация полезности Робинзоном 51

Система уравнений, определяющая необходимые условия на-

личия максимума у функции полезности, будет почти полностью

совпадать с аналогичной системой (1.7) для модели 1. Отличие

лишь в том, что в последней строчке, определяющей частную про-

изводную функции Лагранжа по

Х^

в правой части присутствует /:

3t = I7t -

X • ^1

= 0;

=:Ui-Xai

=0;

3„ =U„-X'a„ =0; (1.32)

По аналогии с (1.11) имеем U/a^ = и^. В этом, конечно, нет ни-

чего неожиданного: ведь параметр / лишь уменьшает величину «по-

лезно используемой» в текущем плане части единичного отрезка Г.

А вот при решении системы уравнений (1.32) необходимо прини-

мать во внимание, что значения неизвестных переменных X|,...,x„, L

определяются теперь не только параметрами

6Z„

но и параметром /:

х^

= х/^(й^,...,й„,/);

х^

=х^(а^,...,а„,1У,

х„ =x,f

(й1,...,й„,/);

(1.33)

L = L^(^i,...,fl„,/);

Х = Х^(й,,...,й„,/).

52 Глава 1. Экономика «робинзонады»

Соответственно косвенная функция полезности будет иметь

следующий вид: U^ = U{a^,...,a^^J). Имея в виду, что по «лемме

об огибающей»

э/

— ГТП7Т"\7'ПРМ'

^^ =

-Х^

(,34)

Таким образом, увеличение трудовых инвестиций на одну

единицу приводит к уменьшению общей полезности в этот пе-

риод на величину

соответствующую предельной полезности

свободного времени.

В то же время во второй период величина общей полезности

должна возрасти, так как благодаря осуществленным в первый

период инвестициям повысится производительность труда. Для

демонстрации этого, а также для выяснения возникающих здесь

количественных взаимосвязей сформулируем модель максимиза-

ции полезности Робинзоном во второй единичный период (при

этом учтем, что инвестиций в этот период больше не будет, а пока-

затели трудоемкости становятся функциями от инвестиций, про-

изведенных в первый период):

max (/(2> = (/(24xP,...,xl2\L<2>), i =

i,...,n

(1.35)

при ограничении (условии связи)

1=1

Соответственно функция Лагранжа для второго периода будет

иметь следующий вид:

3^2^ = и^'\х\'\...,х^^\Ь^'^)

Л^2>

(T-t

af\l).

хр> -

L<2))

(^36)

t=i

Поскольку по «лемме об огибающей» скорость изменения кос-

венной функции полезности равняется скорости изменения функ-

ции Лагранжа в точке максимума, имеем:

Максимизация полезности Робинзоном

Э/

= -X

М(2) ^М(2)

fdflP

+... +

М(2)

d^n

(1.37)

Поскольку

(2)

— отрицательная величина (рост инвестиций

ведет к последующему снижению трудоемкости), постольку

Э/

>0.

Теперь, когда ясны механизмы потерь полезности в первом пе-

риоде и выигрыша полезности во втором периоде, а также способ

обеспечения сопоставимости будущей полезности и текущей (см.

п, 1), мы можем поставить вопрос о нахождении оптимальной ве-

личины трудовых инвестиций в первом периоде.

Отметим следующие особенности математической модели,

адекватной для решения этой задачи. Во-первых, величина инве-

стиций времени, производимых в первый период, превращается

здесь из экзогенно задаваемого параметра в эндогенную перемен-

ную.

Соответственно она должна быть представлена в целевой

функции. Во-вторых, общая величина полезности, реализуемой

индивидом за два периода, должна равняться сумме полезности,

полученной в первом периоде, и дисконтированной величины по-

лезности второго периода. При этом дисконт, как мы видели в

п. 1, является возрастающей функцией от величины инвестиций

dD ^

времени, т.е. —ттг > 0.

(1)

(1.38)

при ограничениях (условиях связи)

(0.^(0 ^^^0)^^(0

1=1

Глава 1. Экономика «робинзонады»

Функция Лагранжа будет иметь следующий

вид:

Х2 •

(2)/г(Оч_(2)/^(2)/ИОчч

r(2)

1=1

(1.39)

- s

вГЧГ'О

•

х,^'Чй,^^Ч/"0)

- Г'

Необходимые условия наличия максимума

функции

Ла-

гранжа:

3i'^

= C/r^-X,.fl|'> =

,(0 _rr(1)

(О

ЗУ

иу'-ХгаУ'

= 0;

3|Nf/r-^,-«r

а(1)

_ гг(0 _

- О-

f^j^^-^)

ЙЭхР>

ЭАР

Э/<'>

D(r")

+ ^.[/(2)(;,(2)(^(2)(;(.)) ;,(2)(^(2)(^(.))д,(2)).

(1.40)

-Я,

Лз •

Д dflP>

скР>

,5^--P('^P^<^^'^)-S2)-Р(/^'^)

= 0;

Зх, =7--Ё«*''-^Г'-^-"'-/'*' =

Максимизация полезности Робинзоном

35"

(7р> •Da<")-X2-af

(/<'>)

ЗР

= t/P

• DU^'^)

Х2 •

йрЧ/") = 0; (1.40)

о(2)

_ tbn

(ттО)

_ > . „(2) _ «.

3|>=^((/Р-Х2)-Х,-жР

а(2)

_ dx,^ . (2) _ .

_ . . (2) _ л.

Зх,

= Г

- S

йРЧ/^'')

•

x^4aj4l''')) -1<" =

3g> = (7f (xp>(«P>(/<'>),...,xf (flf

(/<^>),Z.<2>)

= 0. (1.40)

Решение данной системы уравнений позволяет найти значения

1^^\

D(/^^0,

х1^\ а\^\ хр\ Lp L2, ^t,

>-2' максимизирующие

уро-

56 Глава 1. Экономика «робинзонады»

вень благосостояния индивида за два рассматриваемых периода.

Вместе с тем ввиду громоздкости из этих уравнений затрудни-

тельно вывести ясные закономерности, характеризующие взамо-

отношение различных переменных.

Поэтому упростим нашу задачу. Будем рассматривать вели-

чину полезности как функцию от количества произведенного

композитного блага х. Это значит, что мы здесь отвлекаемся

от свободного времени как фактора удовлетворения потребно-

стей. Исходное положение, в котором находится Робинзон

(рис.

1.6), характеризуется его способностью производить оди-

наковое количество композитного блага в первый и второй пе-

риод (х^ = ^2). Вместе с тем, прибегнув в первом периоде к тру-

довым инвестициям продолжительностью /, он может, сократив

текущее потребление (х] - xf = -

1/а^

< 0), увеличить потребле-

ние будущее: (х\ -

Х2

= (х] - х^)

•

(-1)

•

(1 + г), где 1 + г

—

абсо-

Будущие блага ,

х^

'>*^i='N^.

\\ '*^°

Текущие блага

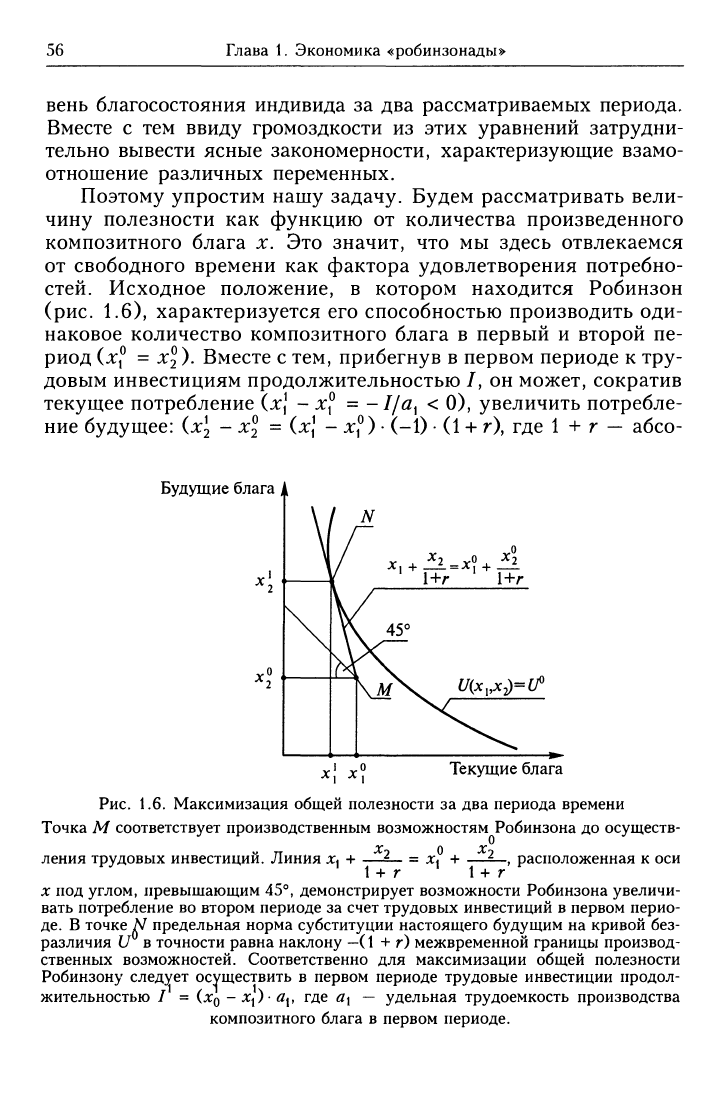
Рис.

1.6. Максимизация общей полезности за два периода времени

Точка М соответствует производственным возможностям Робинзона до осуществ-

^2 -

= X, +

Х2

расположенная к оси

ления трудовых инвестиций. Линия

Хл

\ + г \ + г

X под углом, превышающим 45°, демонстрирует возможности Робинзона увеличи-

вать потребление во втором периоде за счет трудовых инвестиций в первом перио-

де.

В точке

Л^

предельная норма субституции настоящего будущим на кривой без-

различия и в точности равна наклону

—(1

+ г) межвременной границы производ-

ственных возможностей. Соответственно для максимизации общей полезности

Робинзону следует осуществить в первом периоде трудовые инвестиции продол-

жительностью / = (^0

-X|)^|,

где <2| — удельная трудоемкость производства

композитного блага в первом периоде.

Максимизация полезности Робинзоном 57

лютная величина углового коэффициента прямой, определяю-

щей возможности увеличения производства в будущем периоде

за счет возрастающей в результате трудовых инвестиций фондо-

вооруженности труда и соответственно снижающихся удель-

ных трудовых затрат на производство композитного блага. От-

сюда следует, что межвременная граница производственных

возможностей Робинзона может быть записана в таком виде

(при этом мы отбрасываем верхний индекс у х\ и х\)\

(1 +

г)

(1 +

г)

функция Лагранжа для стоящей перед нами проблемы будет

иметь следующий вид:

3 = и{х^уХ2)-^'к

af-xi)

\Х2 Х2)

(1 + г)

(1.42)

Из необходимых условий наличия максимума вытекает сле-

дующая формула абсолютной величины предельной нормы заме-

щения полезности текущей полезностью будущей:

-ii = -(l + r). (1.43)

с/2

Таким образом, предельная ценность текущего потребления

(его норма замещения будущим потреблением) равняется альтер-

нативным издержкам, связанным с упущенным будущим потреб-

лением в результате нереализованных возможностей роста произ-

водительности труда под воздействием трудовых инвестиций.

И напротив, альтернативные издержки будущего потребления мо-

гут быть представлены обратной по отношению к [—(1+ г)] вели-

чиной /г = - -.

(1 + г)

Здесь следует оговориться, что мы не включили в функцию

Лагранжа одно из важных ограничений, состоящее в том, что Ро-

бинзон может обменивать только текущее потребление на буду-

щее,

но не наоборот. Поэтому вполне возможен случай, что усло-

вие касания межвременной функции полезности и межвременной

58 Глава 1. Экономика «робинзонады»

Границы производственных возможностей произойдет правее точ-

ки (х^, Х2), т.е. там, где межвременная граница производствен-

ных возможностей отсутствует (рис. 1.6). Очевидно, что в этом

случае наивысшая из кривых безразличия, доступных Робинзо-

ну, будет проходить через точку (х^, ^2) и, соответственно, ника-

ких трудовых инвестиций он осуществлять не будет.

Решив уравнения, определяющие необходимые условия мак-

симума межвременной функции полезности, получаем маршал-

лианские функции востребованности текущего и будущего по-

требления: х- = x^(k, х^). Подставив их в функцию Лагранжа

(1.43) и продифференцировав последнюю по k, в соответствии с

леммой об огибающей получаем: dU^ / dk = X

•

{х^ - х^). От-

сюда следует, что увеличение г (соответственно уменьшение k),

отражающее возрастающее воздействие трудовых инвестиций на

производительность труда, будет способствовать увеличению ин-

вестиций.

Далее конкретизируем межвременную функцию полезности,

придав ей вид аддитивной функции с дисконтированием полезно-

стей будущих периодов (см. (1.2)). Тогда «условие касания», не-

обходимое для достижения максимума межвременной функцией

полезности для двух последовательных периодов, примет следую-

щий вид:

UXxj) _

+ г

Отсюда видно, что масштабы потребления в различные вре-

менные периоды зависят как от степени «нетерпеливости» потре-

бителей, выражаемой через \

р^

так и от производственных воз-

можностей Робинзона увеличивать производительность своего

труда благодаря трудовым инвестициям в создание средств труда

(1 4- г). В случае равенства г и р оказывается, что в интересах

Робинзона обеспечивать постоянный уровень потребления

х^

= х^ в различные временнь1е отрезки. Тогда же, когда эти

параметры не равны друг другу, Робинзон должен либо увеличи-

вать,

либо уменьшать свое потребление постоянным темпом, опре-

деляемым из решения уравнения (1.44)^

См.:

Silberberg, Е. Ор. cit. Р. 424-425.

Максимизация полезности Робинзоном 59

Модель 3. Природные ресурсы ограниченны

До сих пор мы исходили из того, что Робинзон, определяя наибо-

лее эффективный вариант «времяпрепровождения», не сталкива-

ется ни с какими ограничениями в ресурсах, необходимых для

производства потребляемых им благ х^,...,х„. Между тем для соз-

дания этих благ Робинзону необходимо располагать помимо соб-

ственного времени необходимым количеством соответствующего

природного материала (оставим пока в стороне созданные трудом

самого Робинзона средства труда).

Допустим, в производстве используется т видов ресурсов,

имеющихся в количестве b^,...,b^. Тогда ограниченность этих ре-

сурсов мы можем представить как функцию от создаваемых с их

помощью благ: gXx^,...,x^)<bi. Добавим также естественное требо-

вание неотрицательности количества производимых Робинзоном

потребительных ценностей.

С учетом сказанного модель максимизации степени удовлетво-

рения потребностей Робинзона может быть сформулирована сле-

дующим образом:

max и = и(х^, ..., д:„, L)

при ограничениях (условиях связи)

дЧх,,...,х„)<Ь^; (1.45)

L +

а^-

= Г;

= l,...,w; i = l,...,m.

Общий подход для определения точки максимума у моделей, в

которых ограничения представлены неравенствами, был разрабо-