Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

1.9.2 The Wu–Yang monopole

Wu and Yang (1975) noticed that the geometrical and topological structures

behind the Dirac monopole are best described by ﬁbre bundles. In chapters 9

and 10, we give an account of the Dirac monopole in terms of ﬁbre bundles and

their connections. Here we outline the idea of Wu and Yang without introducing

the ﬁbre bundle. Wu and Yang noted that we may employ more than one vector

potential to describe a monopole. For example, we may avoid singularities if

we adopt A

in the northern hemisphere and A

in the southern hemisphere

of the sphere S surrounding the monopole. These vector potentials yield the

magnetic ﬁeld B = gr/r

, which is non-singular everywhere on the sphere.

On the equator of the sphere, which is the boundary between the northern and

southern hemispheres, A

and A

are related by the gauge transformation,

− A

= grad . To compute this quantity , we employ the result of exercise

1.14,

− A

r sin θ

ˆe

= grad(2gφ) (1.281)

where use has been made of the expression

grad f =

∂ f

∂r

ˆe

∂ f

∂θ

ˆe

r sin θ

∂ f

∂φ

ˆe

Accordingly, the gauge transformation function connecting A

and A

 = 2gφ. (1.282)

Note that  is ill deﬁned at θ = 0andθ = π. Since we perform the gauge

transformation only at θ = π/2, these singularities do not show up in our analysis.

The total ﬂux is

 =

curl A · dS =



curl A

· dS +



curl A

· dS (1.283)

where U

and U

stand for the northern and southern hemispheres respectively.

Stokes’ theorem yields

 =

equator

· ds −

equator

· ds =

equator

( A

− A

) ·ds

equator

grad(2gφ) · ds = 4gπ (1.284)

in agreement with (1.277).

1.9.3 Charge quantization

Consider a point particle with electric charge e and mass m moving in the ﬁeld

of a magnetic monopole of charge g. If the monopole is heavy enough, the

Schr¨odinger equation of the particle takes the form



p −



ψ(r) = Eψ(r). (1.285)

It is easy to show that under the gauge transformation A → A + grad ,the

wavefunction changes as ψ → exp(ie/

hc)ψ. In the present case, A

and A

differ only by the gauge transformation A

− A

= grad(2gφ).Ifψ

and ψ

are

wavefunctions deﬁned on U

and U

respectively, they are related by the phase

change

(r) = exp



−ie



(r). (1.286)

Let us take θ = π/2 and study the behaviour of wavefunctions as we go round

the equator of the sphere from φ = 0toφ = 2π. The wavefunction is required to

be single valued, hence (1.286) forces us to take

2eg

= nn∈

. (1.287)

This is the celebrated Dirac quantization condition for the magnetic charge; if

the magnetic monopole exists, the magnetic charge takes discrete values,

g =

hcn

n ∈

. (1.288)

By the same token, if there exists a magnetic monopole somewhere in the

universe, all the electric charges are quantized.

1.10 Instantons

The vacuum-to-vacuum amplitude in the Euclidean theory is

Z ≡0|0∝



φ e

−S[φ,∂

φ]

(1.289)

where S is the Euclidean action. Equation (1.289) shows that the principal

contribution to Z comes from the values of φ(x) which give the local minima

of S[φ,∂

φ]. In many theories there exist a number of local minima in addition

to the absolute minimum. In the case of non-Abelian gauge theories these minima

are called instantons.

1.10.1 Introduction

Let us consider the SU(2) gauge theory deﬁned in the four-dimensional Euclidean

space

. The action is

S =



x (x) =



x[−

µν

] (1.290)

where the ﬁeld strength is

µν

= ∂

µ ν

− ∂

ν µ

+ g[

] (1.291)

with

≡ A

µν

≡ F

µν

The ﬁeld equation is

µ µν

= ∂

µ µν

+ g[

µν

]=0. (1.292)

In the path integral only those ﬁeld conﬁgurations with ﬁnite action

contribute. Suppose

satisﬁes

→ iU(x)

−1

∂

U(x ) as |x |→∞ (1.293)

where U(x ) is an element of SU(2). We easily ﬁnd that

µν

vanishes for the

of (1.293). We require that on sphere S

of large radius, the gauge potential be

given by (1.293).

Later we show that this conﬁguration is characterized by the way in which

is mapped to the gauge group SU(2). Non-trivial conﬁgurations are those that

cannot be deformed continuously to a uniform conﬁguration. They were proposed

by Belavin et al (1975) and are called instantons.

1.10.2 The (anti-)self-dual solution

In general, solving a second-order differential equation is more difﬁcult than

solving a ﬁrst-order one. It is nice if a second-order differential equation can

be replaced by a ﬁrst-order one which is equivalent to the original problem. Let

us consider the inequality



x tr



µν

±∗

µν

≥ 0. (1.294)

Clearly (1.294) is saturated if

µν

=±∗

µν

. (1.295)

If the positive sign is chosen,

is said to be self-dual while the negative sign

gives an anti-self-dual solution. If (1.295) is satisﬁed, the ﬁeld equation is

automatically satisﬁed since

µ µν

=±

∗

µν

= 0 (Bianchi identity). (1.296)

As we will show in section 10.5, the integral

Q ≡

−1

16π



x tr

µν

∗

µν

(1.297)

is an integer characterizing the way S

is mapped to SU(2). If is self-dual then

Q is positive, and if

is anti-self-dual then Q is negative. From (1.294), we ﬁnd

(note that ∗

µν

∗

µν

)that



x (2

µν

± 2 ∗

µν

∗

µν

) ≥ 0. (1.298)

From this inequality and the deﬁnition of the action, we ﬁnd that

S ≥ 8π

|Q| (1.299)

where the inequality is saturated for (1.295). Let us concentrate on the self-dual

solution

=∗ . We look for an instanton solution of the form

= i f (r )U (x)

−1

∂

U(x ) (1.300)

where r ≡|x| and

f (r) → 1asr →∞ (1.301a)

U(x) =

− ix

). (1.301b)

Substituting (1.300) into (1.295), we ﬁnd that f satisﬁes

d f (r)

= 2 f (1 − f ). (1.302)

The solution that satisﬁes the boundary condition (1.301a) is

f (r) =

+ λ

(1.303)

where λ is a parameter that speciﬁes the size of the instanton. Substituting this

into (1.300) we ﬁnd that

(x ) =

+ λ

U(x )

−1

∂

U(x ) (1.304)

and the corresponding ﬁeld strength

µν

(x ) =

4λ

+ λ

µν

(1.305)

where

≡

[σ

,σ

] σ

≡

=−σ

. (1.306)

This solution gives Q =+1andS = 8π

Problems

1.1 Consider a Hamiltonian of the form

H =







∂φ

∂t



(∇φ)

+ V (φ)



where V (φ) (≥ 0) is a potential. If φ is a time-independent classical solution, we

may drop the ﬁrst term and write H [φ]=H

[φ]+H

[φ],where

[φ]≡



x (∇φ)

[φ]≡



xV(φ).

(1) Consider a scale transformation φ(x ) → φ(λx). Show that H

[φ]

transforms as

[φ]→H

[φ]=λ

(n−2)

[φ] H

[φ]→H

[φ]=λ

−n

[φ].

(2) Suppose φ satisﬁes the ﬁeld equation. Show that

(2 −n)H

[φ]−nH

[φ]=0.

[Hint:Taketheλ-derivative of H

[φ]+H

[φ] and put λ = 1.]

(3) Show that time-independent topological excitations of H [φ] exist if and

only if n = 1(Derrick’s theorem). Consider ways out of this restriction.

MATHEMATICAL PRELIMINARIES

In the present chapter we introduce elementary concepts in the theory of maps,

vector spaces and topology. A modest knowledge of undergraduate mathematics,

such as set theory, calculus, complex analysis and linear algebra is assumed.

The main purpose of this book is to study the application of the theory of

manifolds to the problems in physics. Vector spaces and topology are, in a sense,

two extreme viewpoints of manifolds. A manifold is a space which locally looks

(or

) but not necessarily globally. As a ﬁrst approximation, we may

model a small part of a manifold by a Euclidean space

(or

)(asmall

area around a point on a surface can be approximated by the tangent plane at

that point); this is the viewpoint of a vector space. In topology, however, we

study the manifold as a whole. We want to study the properties of manifolds and

classify manifolds using some sort of ‘measures’. Topology usually comes with

an adjective: algebraic topology, differential topology, combinatorial topology,

general topology and so on. These adjectives refer to the measure we use when

classifying manifolds.

2.1 Maps

2.1.1 Deﬁnitions

Let X and Y be sets. A map (or mapping) f is a rule by which we assign y ∈ Y

for each x ∈ X . We write

f : X → Y. (2.1)

If f is deﬁned by some explicit formula, we may write

f : x → f (x ) (2.2)

There may be more than two elements in X that correspond to the same y ∈ Y .A

subset of X whose elements are mapped to y ∈ Y under f is called the inverse

image of y, denoted by f

−1

(y) ={x ∈ X |f (x ) = y}.ThesetX is called

the domain of the map while Y is called the range of the map. The image of

the map is f (X) ={y ∈ Y |y = f (x) for some x ∈ X}⊂Y .Theimage

f (X) is also denoted by im f . The reader should note that a map cannot be

deﬁned without specifying the domain and the range. Take f (x ) = exp x ,for

example. If both the domain and the range are

, f (x) =−1hasnoinverse

image. If. however, the domain and the range are the complex plane ,weﬁnd

−1

(−1) ={(2n +1)πi|n ∈ Z}. The domain X and the range Y are as important

as f itself in specifying a map.

Example 2.1. Let f :

→ be given by f (x ) = sin x . We also write

f : x → sin x. The domain and the range are

and the image f ( ) is [−1, 1].

The inverse image of 0 is f

−1

(0) ={nπ |n ∈ }. Let us take the same function

f (x ) = sin x = (e

− e

−ix

)/2i but f : → this time. The image f (C) is the

whole complex plane

Deﬁnition 2.1. If a map satisﬁes a certain condition it bears a special name.

(a) A map f : X → Y is called injective (or one to one)ifx = x



implies

f (x ) = f (x



(b) A map f : X → Y is called surjective (or onto) if for each y ∈ Y there

exists at least one element x ∈ X such that f (x) = y.

Example 2.2. Amap f :

→ deﬁned by f : x → ax (a ∈ −{0}) is

bijective. f :

→ deﬁned by f : x → x

is neither injective nor surjective.

f :

→ given by f : x → exp x is injective but not surjective.

Exercise 2.1. Amap f :

→ deﬁned by f : x → sin x is neither injective

nor surjective. Restrict the domain and the range to make f bijective.

Example 2.3. Let M be an element of the general linear group GL(n,

) whose

matrix representation is given by n ×n matrices with non-vanishing determinant.

Then M :

→

, x → Mx is bijective. If det M = 0, it is neither injective

nor surjective.

A constant map c : X → Y is deﬁned by c(x ) = y

where y

is a ﬁxed

element in Y and x is an arbitrary element in X . Given a map f : X → Y ,we

may think of its restriction to A ⊂ X , which is denoted as f |

: A → Y .Given

two maps f : X → Y and g : Y → Z ,thecomposite map of f and g is a map

g ◦ f : X → Z deﬁned by g ◦ f (x) = g( f (x )). A diagram of maps is called

commutative if any composite maps between a pair of sets do not depend on how

they are composed. For example, in ﬁgure 2.1, f ◦ g = h ◦ j and f ◦ g = k etc.

Exercise 2.2. Let f :

→ be deﬁned by f : x → x

and g : → by

g : x → exp x.Whatareg ◦ f :

→ and f ◦ g : → ?

If A ⊂ X ,aninclusion map i : A → X is deﬁned by i (a) = a for any

a ∈ A. An inclusion map is often written as i : A → X.Theidentity map

: X → X is a special case of an inclusion map, for which A = X.If

f : X → Y deﬁned by f : x → f (x ) is bijective, there exists an inverse map

−1

: Y → X, such that f

−1

: f (x) → x, which is also bijective. The maps f

Figure 2.1. A commutative diagram of maps.

and f

−1

satisfy f ◦ f

−1

= id

and f

−1

◦ f = id

.Conversely,if f : X → Y

and g : Y → X satisfy f ◦g = id

and g ◦ f = id

,then f and g are bijections.

This can be proved from the following exercise.

Exercise 2.3. Show that if f : X → Y and g : Y → X satisfy g ◦ f = id

, f is

injective and g is surjective. If this is applied to f ◦ g = id

as well, we obtain

the previous result.

Example 2.4. Let f :

→ (0, ∞) be a bijection deﬁned by f : x → exp x.

Then the inverse map f

−1

: (0, ∞) → is f

−1

: x → ln x .Letg :

(−π/2,π/2) → (−1, 1) be a bijection deﬁned by g : x → sin x.Theinverse

map is g

−1

: x → sin

−1

Exercise 2.4. The n-dimensional Euclidean group E

is made of an n-

dimensional translation a : x → x +a (x , a ∈

) andanO(n) rotation R : x →

Rx, R ∈ O(n). A general element (R, a) of E

acts on x by (R, a) : x → Rx+a.

The product is deﬁned by (R

, a

) × (R

, a

) : x → R

x + a

) + a

,that

is, (R

, a

) ◦(R

, a

) = (R

, R

). Show that the maps a, R and (R, a)

are bijections. Find their inverse maps.

Suppose certain algebraic structures (product or addition, say) are endowed

with the sets X and Y .If f : X → Y preserves these algebraic structures, then f

is called a homomorphism. For example, let X be endowed with a product. If f

is a homomorphism, it preserves the product, f (ab) = f (a) f (b). Note that ab is

deﬁned by the product rule in X ,and f (a) f (b) by that in Y . If a homomorphism

f is bijective, f is called an isomorphism and X is said to be isomorphic to Y ,

denoted x

∼

2.1.2 Equivalence relation and equivalence class

Some of the most important concepts in mathematics are equivalence relations

and equivalence classes. Although these subjects are not directly related to maps,

it is appropriate to deﬁne them at this point before we proceed further. A relation

R deﬁned in a set X is a subset of X

. If a point (a, b) ∈ X

is in R, we may write

aRb. For example, the relation > is a subset of

.If(a, b) ∈ >,thena > b.

Deﬁnition 2.2. An equivalence relation ∼ is a relation which satisﬁes the

following requirements:

(i) a ∼ a (reﬂective).

(ii) If a ∼ b,thenb ∼ a (symmetric).

(iii) If a ∼ b and b ∼ c,thena ∼ c (transitive).

Exercise 2.5. If an integer is divided by 2, the remainder is either 0 or 1. If two

integers n and m yield the same remainder, we write m ∼ n. Show that ∼ is an

equivalence relation in

Given a set X and an equivalence relation ∼, we have a partition of X into

mutually disjoint subsets called equivalence classes. A class [a] is made of all

the elements x in X such that x ∼ a,

[a]={x ∈ X|x ∼ a} (2.3)

[a] cannot be empty since a ∼ a. We now prove that if [a]∩[b] =∅then

[a]=[b]. First note that a ∼ b.(Since[a]∩[b] =∅there is at least one

element in [a]∩[b] that satisﬁes c ∼ a and c ∼ b. From the transitivity, we

have a ∼ b.) Next we show that [a]⊂[b]. Take an arbitrary element a



in [a];



∼ a.Thena ∼ b implies b ∼ a



,thatisa



∈[b]. Thus, we have [a]⊂[b].

Similarly, [a]⊃[b] can be shown and it follows that [a]=[b]. Hence, two

classes [a] and [b] satisfy either [a]=[b] or [a]∩[b]=∅. In this way a set X

is decomposed into mutually disjoint equivalence classes. The set of all classes

is called the quotient space, denoted by X/ ∼. The element a (or any element

in [a]) is called the representative of a class [a]. In exercise 2.5, the equivalence

relation ∼ divides integers into two classes, even integers and odd integers. We

may choose the representative of the even class to be 0, and that of the odd class

to be 1. We write this quotient space

/ ∼. / ∼ is isomorphic to

,thecyclic

group of order 2, whose algebra is deﬁned by 0 + 0 = 0, 0 + 1 = 1 + 0 = 1

and 1 + 1 = 0. If all integers are divided into equivalence classes according to

the remainder of division by n, the quotient space is isomorphic to

, the cyclic

group of order n.

Let X be a space in our usual sense. (To be more precise, we need the

notion of topological space, which will be deﬁned in section 2.3. For the time

being we depend on our intuitive notion of ‘space’.) Then quotient spaces may

be realized as geometrical ﬁgures. For example, let x and y be two points in

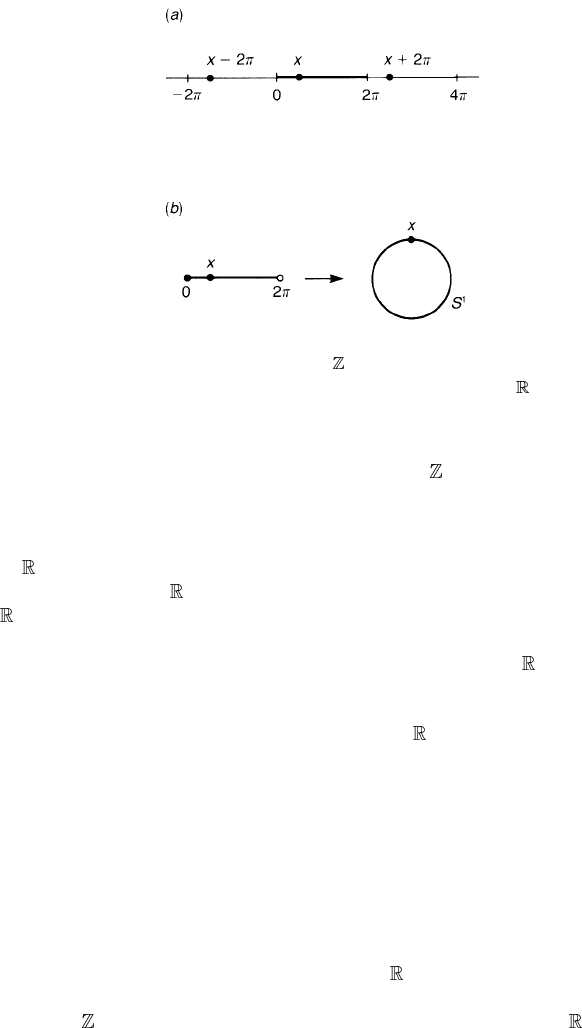
Figure 2.2. In (a) all the points x + 2nπ, n ∈ are in the same equivalence class [x].We

may take x ∈[0, 2π) as a representative of [x].(b) The quotient space

/ ∼ is the circle

Introduce a relation ∼ by: x ∼ y if there exists n ∈ such that y = x + 2πn.

It is easily shown that ∼ is an equivalence relation. The class [x ] is the set

{...,x −2π, x , x +2π,...}. A number x ∈[0, 2π) serves as a representative of

an equivalence class [x], see ﬁgure 2.2(a). Note that 0 and 2π are different points

but, according to the equivalence relation, these points are looked upon as

the same element in

/ ∼. We arrive at the conclusion that the quotient space

/ ∼ is the circle S

={e

iθ

|0 ≤ θ<2π}; see ﬁgure 2.2(b). Note that a point

ε is close to a point 2π − ε for inﬁnitesimal ε. Certainly this is the case for S

where an angle ε is close to an angle 2π − ε, but not the case for

. The concept

of closeness of points is one of the main ingredients of topology.

Example 2.5. (a) Let X be a square disc {(x , y) ∈

||x|≥1, |y|≥1}.Ifwe

identify the points on a pair of facing edges, (−1, y) ∼ (1, y), for example, we

obtain the cylinder, see ﬁgure 2.3(a). If we identify the points (−1, −y) ∼ (1, y),

we ﬁnd the M¨obius strip, see ﬁgure 2.3(b).[Remarks: If readers are not familiar

with the M¨obius strip, they may take a strip of paper and glue up its ends after

a π-twist. Because of the twist, one side of the strip has been joined to the

other side, making the surface single sided. The M¨obius strip is an example

of a non-orientable surface, while the cylinder has deﬁnite sides and is said to

be orientable. Orientability will be discussed in terms of differential forms in

section 5.5.]

(b) Let (x

, y

) and (x

, y

) be two points in

and introduce an equivalence

relation ∼ by: (x

, y

) ∼ (x

, y

) if x

= x

+ 2πn

and y

= y

+ 2πn

, n

∈ .Then∼ is an equivalence relation. The quotient space

/ ∼ is

the torus T

(the surface of a doughnut), see ﬁgure 2.4(a). Alternatively, T