Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

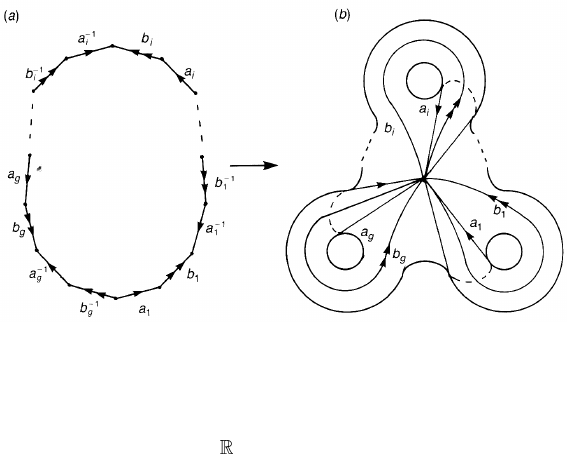
Figure 2.13. The polygon (a) whose edges are identiﬁed is the torus 

with genus g.

2.3 Show that two ﬁgures in ﬁgure 2.109(b) are homeomorphic to each other. Find

how to unlink the right ﬁgure in

2.4 Show that there are only ﬁve regular polyhedra: a tetrahedron, a hexahedron,

an octahedron, a dodecahedron and an icosahedron. [Hint: Use Euler’s theorem.]

HOMOLOGY GROUPS

Among the topological invariants the Euler characteristic is a quantity readily

computable by the ‘polyhedronization’ of space. The homology groups are

reﬁnements, so to speak, of the Euler characteristic. Moreover, we can easily read

off the Euler characteristic from the homology groups. Let us look at ﬁgure 3.1.

In ﬁgure 3.1(a), the interior is included but not in ﬁgure 3.1(b). How do we

characterize this difference? An obvious observation is that the three edges of

ﬁgure 3.1(a) form a boundary of the interior while the edges of ﬁgure 3.1(b)do

not (the interior is not apartofﬁgure3.1(b)). Clearly the edges in both cases

form a closed path (loop), having no boundary. In other words, the existence of

a loop that is not a boundary of some area implies the existence of a hole within

the loop. This is our guiding principle in classifying spaces here: ﬁnd a region

without boundaries, which is not itself a boundary of some region. This principle

is mathematically elaborated into the theory of homology groups.

Our exposition follows Armstrong (1983), Croom (1978) and Nash and Sen

(1983). An introduction to group theory is found in Fraleigh (1976).

3.1 Abelian groups

The mathematical structures underlying homology groups are ﬁnitely generated

Abelian groups. Throughout this chapter, the group operation is denoted by +

since all the groups considered here are Abelian (commutative). The unit element

is denoted by 0.

3.1.1 Elementary group theory

Let G

and G

be Abelian groups. A map f : G

→ G

is said to be a

homomorphism if

f (x + y) = f (x) + f (y) (3.1)

for any x, y ∈ G

.1ff is also a bijection, f is called an isomorphism.Ifthere

exists an isomorphism f : G

→ G

, G

is said to be isomorphic to G

, denoted

by G

∼

. For example, a map f : →

={0, 1} deﬁned by

f (2n) = 0 f (2n + 1) = 1

Figure 3.1. (a) is a solid triangle while (b) is the edges of a triangle without an interior.

is a homomorphism. Indeed

f (2m + 2n) = f (2(m + n)) = 0 = 0 + 0 = f (2m) + f (2n)

f (2m + 1 + 2n + 1) = f (2(m + n + 1)) = 0 = 1 + 1

= f (2m + 1) + f (2n + 1)

f (2m + 1 + 2n) = f (2(m + n) + 1) = 1 = 1 +0

= f (2m + 1) + f (2n).

A subset H ⊂ G is a subgroup if it is a group with respect to the group

operation of G. For example,

≡{kn|n ∈ } k ∈

is a subgroup of , while

={0, 1} is not.

Let H be a subgroup of G.Wesayx, y ∈ G are equivalent if

x − y ∈ H (3.2)

and write x ∼ y. Clearly ∼ is an equivalence relation. The equivalence class to

which x belongs is denoted by [x ].LetG/H be the quotient space. The group

operation + in G naturally induces the group operation + in G/H by

[x]+[y]=[x + y]. (3.3)

Note that + on the LHS is an operation in G/H while + on the RHS is that in G.

The operation in G/H should be independent of the choice of representatives. In

fact, if [x



]=[x ], [y



]=[y],thenx − x



= h, y − y



= g for some h, g ∈ H

and we ﬁnd that



+ y



= x + y − (h + g) ∈[x + y]

Furthermore, G/H becomes a group with this operation, since H is always a

normal subgroup of G; see example 2.6. The unit element of G/H is [0]=[h],

h ∈ H .IfH = G,0− x ∈ G for any x ∈ G and G/G has just one element [0].

If H ={0}, G/H is G itself since x − y = 0 if and only if x = y.

Example 3.1. Let us work out the quotient group

/2 . For even numbers

we have 2n − 2m = 2(n − m) ∈ 2

and [2m]=[2n]. For odd numbers

(2n +1)−(2m +1) = 2(n −m) ∈ 2

and [2m +1]=[2n +1]. Even numbers and

odd numbers never belong to the same equivalence class since 2n−(2m+1)/∈ 2

Thus, it follows that

/2 ={[0], [1]}. (3.4)

If we deﬁne an isomorphism ϕ :

/2 →

by ϕ([0]) = 0andϕ([1]) = 1, we

ﬁnd

∼

. For general k ∈ ,wehave

∼

. (3.5)

Lemma 3.1. Let f : G

→ G

be a homomorphism. Then

(a) ker f ={x|x ∈ G

, f (x) = 0} is a subgroup of G

(b) im f ={x|x ∈ f (G

) ⊂ G

} is a subgroup of G

Proof.(a)Letx , y ∈ ker f .Thenx +y ∈ ker f since f (x +y) = f (x) + f (y) =

0+0 = 0. Note that 0 ∈ ker f for f (0) = f (0)+ f (0).Wealsohave−x ∈ ker f

since f (0) = f (x − x) = f (x) + f (−x) = 0.

(b) Let y

= f (x

), y

= f (x

) ∈ im f where x

, x

∈ G

.Sincef is a

homomorphism we have y

= f (x

) + f (x

) = f (x

) ∈ im f . Clearly

0 ∈ im f since f (0) = 0. If y = f (x ), −y ∈ im f since 0 = f (x − x) =

f (x ) + f (−x) implies f (−x) =−y.

Theorem 3.1. (Fundamental theorem of homomorphism)Let f : G

→ G

be a homomorphism. Then

/ker f

∼

im f. (3.6)

Proof. Both sides are groups according to lemma 3.1. Deﬁne a map ϕ :

/ ker f → im f by ϕ([x ]) = f (x). This map is well deﬁned since for



∈[x], there exists h ∈ ker f such that x



= x + h and f (x



) = f (x + h) =

f (x ) + f (h) = f (x). Now we show that ϕ is an isomorphism. First, ϕ is a

homomorphism,

ϕ([x]+[y]) = ϕ([x + y]) = f (x + y)

= f (x) + f (y) = ϕ([x ]) + ϕ([y]).

Second, ϕ is one to one: if ϕ([x ]) = ϕ([y]),then f (x) = f (y) or f (x) − f (y) =

f (x − y) = 0. This shows that x − y ∈ ker f and [x]=[y]. Finally, ϕ is onto:

if y ∈ im f , there exists x ∈ G

such that f (x) = y = ϕ([x ]).

Example 3.2. Let f : →

be deﬁned by f (2n) = 0and f (2n+1) = 1. Then

ker f = 2

and im f =

are groups. Theorem 3.1 states that /2

∼

,in

agreement with example 3.1.

3.1.2 Finitely generated Abelian groups and free Abelian groups

Let x be an element of a group G.Forn ∈

, nx denotes

x +···+x

-. /

(if n > 0)

and

(−x) +···+(−x )

-. /

|n|

(if n < 0).

If n = 0, we put 0x = 0. Take r elements x

,...,x

of G. The elements of G of

the form

+···+n

∈ , 1 ≤ i ≤ r) (3.7)

form a subgroup of G, which we denote H . H is called a subgroup of G

generated by the generators x

,...,x

.IfG itself is generated by ﬁnite

elements x

,...,x

, G is said to be ﬁnitely generated.Ifn

+···+n

= 0

is satisﬁed only when n

= ··· = n

= 0, x

,...,x

are said to be linearly

independent.

Deﬁnition 3.1. If G is ﬁnitely generated by r linearly independent elements, G is

called a free Abelian group of rank r .

Example 3.3.

is a free Abelian group of rank 1 ﬁnitely generated by 1 (or −1).

Let

⊕ be the set of pairs {(i, j)|i, j ∈ }. It is a free Abelian group of rank 2

ﬁnitely generated by generators (1, 0) and (0, 1). More generally

⊕ ⊕···⊕

, -. /

is a free Abelian group of rank r. The group

={0, 1} is ﬁnitely generated by

1butisnot free since 1 is not linearly independent (note 1 + 1 = 0).

3.1.3 Cyclic groups

If G is generated by one element x, G ={0, ±x, ±2x ,...}, G is called a cyclic

group.Ifnx = 0foranyn ∈

−{0},itisaninﬁnite cyclic group while if

nx = 0forsomen ∈

−{0},aﬁnite cyclic group.LetG be a cyclic group

generated by x and let f :

→ G be a homomorphism deﬁned by f (n) = nx.

f maps

onto G but not necessarily one to one. From theorem 3.1, we have

G = im f

∼

/ ker f .LetN be the smallest positive integer such that Nx = 0.

Clearly

ker f ={0, ±N, ±2N,...}=N

(3.8)

and we have

∼

. (3.9)

If G is an inﬁnite cyclic group, then ker f ={0} and G

∼

. Any inﬁnite cyclic

group is isomorphic to

while a ﬁnite cyclic group is isomorphic to some

We will need the following lemma and theorem in due course. We ﬁrst state

the lemma without proof.

Lemma 3.2. Let G be a free Abelian group of rank r and let H (=∅) be a subgroup

of G. We may always choose p generators x

,...,x

, out of r generators of G

so that k

,...,k

generate H . Thus, H

∼

⊕ ... ⊕ k

and H is of

rank p.

Theorem 3.2. (Fundamental theorem of ﬁnitely generated Abelian groups)

Let G be a ﬁnitely generated Abelian group (not necessarily free) with m

generators. Then G is isomorphic to the direct sum of cyclic groups,

∼

⊕···⊕

, -. /

⊕

⊕···⊕

(3.10)

where m = r + p. The number r is called the rank of G.

Proof.LetG be generated by m elements x

,...,x

and let

f :

⊕···⊕

, -. /

→ G

be a surjective homomorphism,

f (n

,...,n

) = n

+···+n

Theorem 3.1 states that

⊕···⊕

, -. /

/ ker f

∼

Since ker f is a subgroup of

⊕···⊕

, -. /

lemma 3.2 claims that if we choose the generators properly, we have

ker f

∼

⊕···⊕k

We ﬁnally obtain

∼

⊕···⊕

, -. /

/ ker f

∼

⊕···⊕

, -. /

/(k

⊕···⊕k

)

∼

⊕···⊕

, -. /

m−p

⊕

⊕···⊕

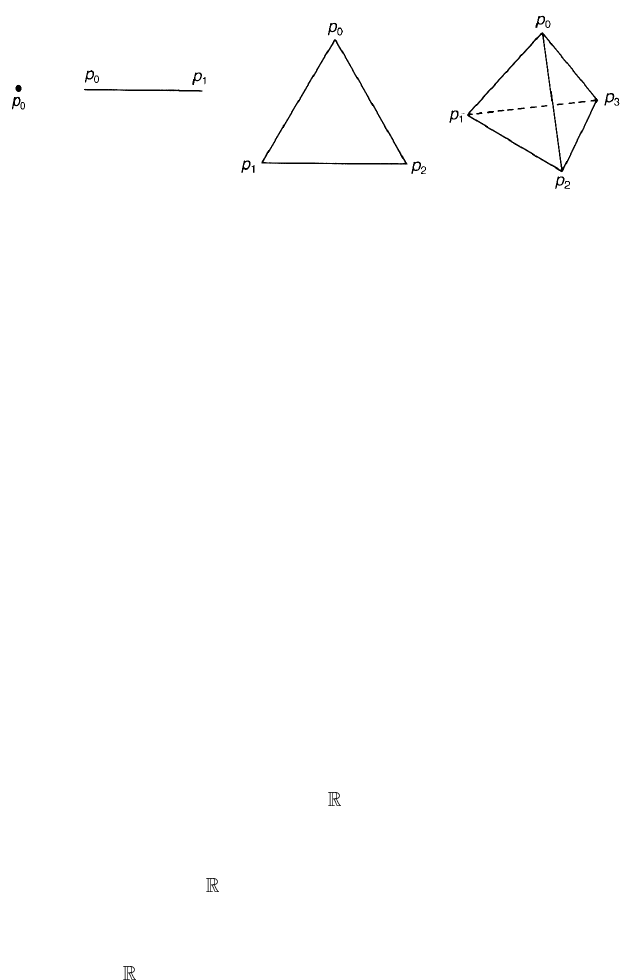
Figure 3.2. 0-, 1-, 2- and 3-simplexes.

3.2 Simplexes and simplicial complexes

Let us recall how the Euler characteristic of a surface is calculated. We ﬁrst

construct a polyhedron homeomorphic to the given surface, then count the

numbers of vertices, edges and faces. The Euler characteristic of the polyhedron,

and hence of the surface, is then given by equation (2.31). We abstract this

procedure so that we may represent each part of a ﬁgure by some standard object.

We take triangles and their analogues in other dimensions, called simplexes, as

the standard objects. By this standardization, it becomes possible to assign to

each ﬁgure Abelian group structures.

3.2.1 Simplexes

Simplexes are building blocks of a polyhedron. A 0-simplex p

 is a point, or

a vertex, and a 1-simplex p

 is a line, or an edge. A 2-simplex p

 is

deﬁned to be a triangle with its interior included and a 3-simplex p

 is

a solid tetrahedron (ﬁgure 3.2). It is common to denote a 0-simplex without the

bracket; p

 may be also written as p

. It is easy to continue this construction

to any r -simplex p

...p

. Note that for an r -simplex to represent an r -

dimensional object, the vertices p

must be geometrically independent, that is, no

(r − 1)-dimensional hyperplane contains all the r + 1 points. Let p

,...,p

be points geometrically independent in

where m ≥ r.Ther -simplex

=p

,...,p

 is expressed as



x ∈



x =



i=0

, c

≥ 0,



i=0

= 1



. (3.11)

,...,c

) is called the barycentric coordinate of x.Sinceσ

is a bounded and

closed subset of

, it is compact.

Let q be an integer such that 0 ≤ q ≤ r. If we choose q + 1 points

,...,p

out of p

,...,p

,theseq + 1 points deﬁne a q-simplex σ

p

,...,p

, which is called a q-face of σ

. We write σ

≤ σ

if σ

is a face of

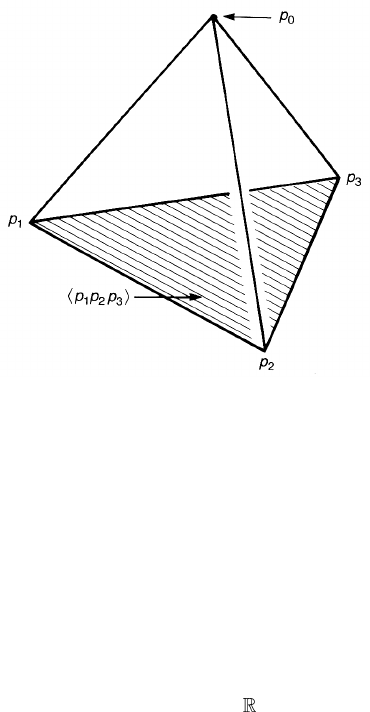
Figure 3.3. A 0-face p

and a 2-face p

 of a 3-simplex p

.

.Ifσ

= σ

,wesayσ

is a proper face of σ

, denoted as σ

<σ

. Figure 3.3

shows a 0-face p

and a 2-face p

 of a 3-simplex p

.Thereare

one 3-face, four 2-faces, six 1-faces and four 0-faces. The reader should verify

that the number of q-faces in an r-simplex is



r + 1

q + 1



. A 0-simplex is deﬁned

to have no proper faces.

3.2.2 Simplicial complexes and polyhedra

Let K be a set of ﬁnite number of simplexes in

. If these simplexes are nicely

ﬁtted together, K is called a simplicial complex. By ‘nicely’ we mean:

(i) an arbitrary face of a simplex of K belongs to K ,thatis,ifσ ∈ K and



≤ σ then σ



∈ K ;and

(ii) if σ and σ



are two simplexes of K , the intersection σ ∩ σ



is either empty

or a common face of σ and σ



,thatis,ifσ, σ



∈ K then either σ ∩ σ



=∅

or σ ∩ σ



≤ σ and σ ∩ σ



≤ σ



For example, ﬁgure 3.4(a) is a simplicial complex but ﬁgure 3.4(b) is not.

The dimension of a simplicial complex K is deﬁned to be the largest dimension

of simplexes in K .

Example 3.4. Let σ

be an r -simplex and K ={σ



|σ



≤ σ

} be the set of

faces of σ

. K is an r-dimensional simplicial complex. For example, take

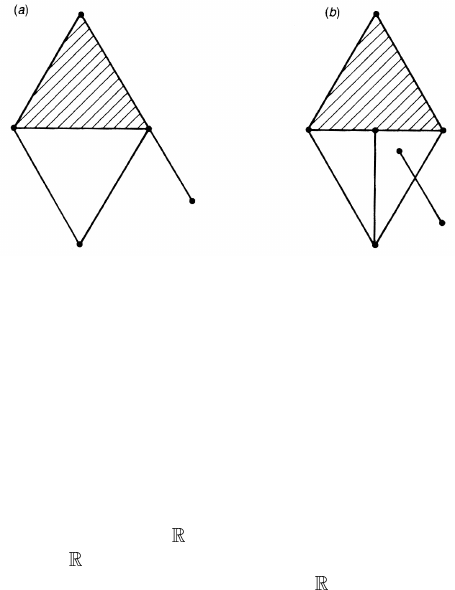
Figure 3.4. (a) is a simplicial complex but (b) is not.

=p

 (ﬁgure 3.3). Then

K ={p

, p

, p

, p

,

p

, p

,

p

, p

}. (3.12)

A simplicial complex K is a set whose elements are simplexes. If each

simplex is regarded as a subset of

(m ≥ dim K ), the union of all the simplexes

becomes a subset of

. This subset is called the polyhedron |K | of a simplicial

complex K . The dimension of |K | as a subset of

is the same as that of K ;

dim |K |=dim K .

Let X be a topological space. If there exists a simplicial complex K and a

homeomorphism f :|K |→X, X is said to be triangulable and the pair (K, f )

is called a triangulation of X . Given a topological space X, its triangulation is

far from unique. We will be concerned with triangulable spaces only.

Example 3.5. Figure 3.5(a) is a triangulation of a cylinder S

×[0, 1]. The reader

might think that somewhat simpler choices exist, ﬁgure 3.5(b), for example. This

is, however, not a triangulation since, for σ

=p

 and σ



=p

,we

ﬁnd σ

∩ σ



=p

∪p

, which is neither empty nor a simplex.

3.3 Homology groups of simplicial complexes

3.3.1 Oriented simplexes

We may assign orientations to an r -simplex for r ≥ 1. Instead of ... for an

unoriented simplex, we will use (...)to denote an oriented simplex. The symbol

is used to denote both types of simplex. An oriented 1-simplex σ

= ( p

) is

a directed line segment traversed in the direction p

→ p

(ﬁgure 3.6(a)). Now

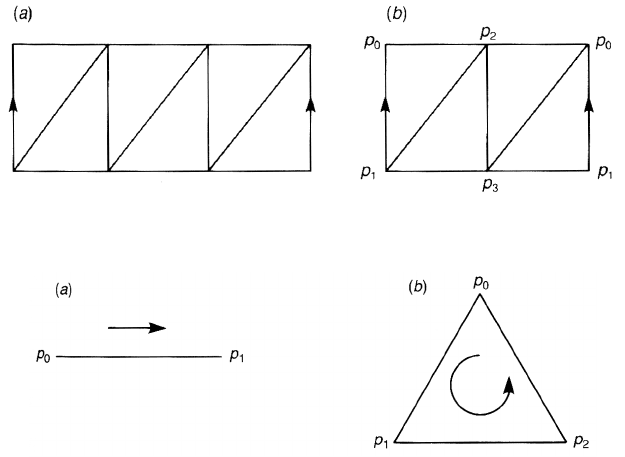
Figure 3.5. (a) is a triangulation of a cylinder while (b) is not.

Figure 3.6. An oriented 1-simplex (a) and an oriented 2-simplex (b).

( p

) should be distinguished from ( p

). We require that

( p

) =−( p

). (3.13)

Here ‘−’ in front of ( p

) should be understood in the sense of a ﬁnitely

generated Abelian group. In fact, ( p

) is regarded as the inverse of ( p

Going from p

to p

followed by going from p

to p

means going nowhere,

( p

) + ( p

) = 0, hence −( p

) = ( p

Similarly, an oriented 2-simplex σ

= ( p

) is a triangular region

with a prescribed orientation along the edges (ﬁgure 3.6(b)). Observe that

the orientation given by p

is the same as that given by p

or p

but opposite to p

, p

or p

. We require that

( p

) = ( p

)

=−(p

) =−( p

Let P be a permutation of 0, 1, 2

P =



012

ijk



These relations are summarized as

( p

) = sgn(P)( p

)