Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

where sgn(P) =+1 (−1) if P is an even (odd) permutation.

An oriented 3-simplex σ

= ( p

) is an ordered sequence of four

vertices of a tetrahedron. Let

P =



0123

ijkl



be a permutation. We deﬁne

( p

) = sgn(P)( p

It is now easy to construct an oriented r-simplex for any r ≥ 1. The

formal deﬁnition goes as follows. Take r + 1 geometrically independent points

, p

,...,p

.Let{p

, p

,...,p

} be a sequence of points obtained by

a permutation of the points p

,...,p

.Wedeﬁne{p

,...,p

}and {p

,...,p

}

to be equivalent if

P =



01... r

... i



is an even permutation. Clearly this is an equivalence relation, the equivalence

class of which is called an oriented r-simplex. There are two equivalence

classes, one consists of even permutations of p

,...,p

, the other of odd

permutations. The equivalence class (oriented r-simplex) which contains

,...,p

} is denoted by σ

= ( p

...p

), while the other is denoted by

−σ

=−( p

...p

).Inotherwords,

( p

...p

) = sgn(P)( p

...p

). (3.14)

For r = 0, we formally deﬁne an oriented 0-simplex to be just a point

= p

3.3.2 Chain group, cycle group and boundary group

Let K ={σ

} be an n-dimensional simplicial complex. We regard the simplexes

in K as oriented simplexes and denote them by the same symbols σ

remarked before.

Deﬁnition 3.2. The r-chain group C

(K ) of a simplicial complex K is a free

Abelian group generated by the oriented r -simplexes of K .Ifr > dim K , C

(K )

is deﬁned to be 0. An element of C

(K ) is called an r-chain.

Let there be I

r-simplexes in K . We denote each of them by σ

r,i

(1 ≤ i ≤

).Thenc ∈ C

(K ) is expressed as

c =



i=1

r,i

∈ . (3.15)

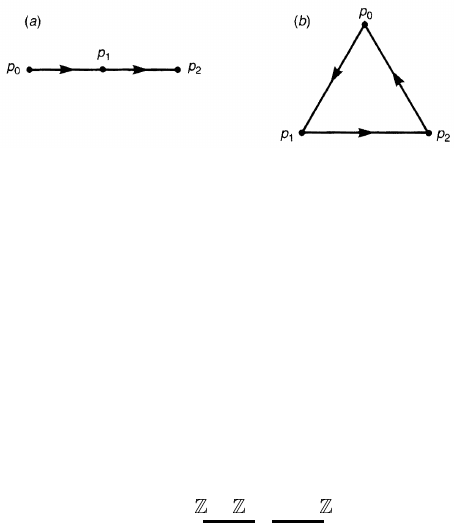
Figure 3.7. (a) An oriented 1-simplex with a ﬁctitious boundary p

.(b) A simplicial

complex without a boundary.

The integers c

are called the coefﬁcients of c. The group structure is given as

follows. The addition of two r-chains, c =



r,i

and c







r,i

,is

c + c





+ c



)σ

r,i

. (3.16)

The unit element is 0 =



0 · σ

r,i

, while the inverse element of c is −c =



(−c

)σ

r,i

.[Remark: An oppositely oriented r-simplex −σ

is identiﬁed with

(−1)σ

∈ C

(K ).] Thus, C

(K ) is a free Abelian group of rank I

(K )

∼

⊕ ⊕···⊕

, -. /

. (3.17)

Before we deﬁne the cycle group and the boundary group, we need to

introduce the boundary operator. Let us denote the boundary of an r -simplex

by ∂

. ∂

should be understood as an operator acting on σ

to produce its

boundary. This point of view will be elaborated later. Let us look at the boundaries

of lower-dimensional simplexes. Since a 0-simplex has no boundary, we deﬁne

∂

= 0. (3.18)

For a 1-simplex ( p

),wedeﬁne

∂

( p

) = p

− p

. (3.19)

The reader might wonder about the appearance of a minus sign in front of p

This is again related to the orientation. The following examples will clarify this

point. In ﬁgure 3.7(a), an oriented 1-simplex (p

) is divided into two, ( p

)

and ( p

). We agree that the boundary of ( p

) is {p

}∪{p

} and so should

be that of ( p

) + ( p

).If∂

( p

) were deﬁned to be p

+ p

, we would

have ∂

( p

) + ∂

( p

) = p

+ p

. This is not desirable since p

is a ﬁctitious boundary. If, instead, we take ∂

( p

) = p

− p

, we will have

∂

( p

) + ∂

( p

) = p

− p

+ p

− p

= p

− p

as expected. The next

example is the triangle of ﬁgure 3.7(b). It is the sum of three oriented 1-simplexes,

( p

) + ( p

). We agree that it has no boundary. If we insisted on

the rule ∂

( p

) = p

+ p

, we would have

∂

( p

) + ∂

( p

) + ∂

( p

) = p

+ p

which contradicts our intuition. If, on the other hand, we take ∂

( p

) =

− p

,wehave

∂

( p

) + ∂

( p

) + ∂

( p

) = p

− p

+ p

− p

+ p

− p

= 0

as expected. Hence, we put a plus sign if the ﬁrst vertex is omitted and a minus

sign if the second is omitted. We employ this fact to deﬁne the boundary of a

general r-simplex.

Let σ

( p

...p

)(r > 0) be an oriented r-simplex. The boundary ∂

is an (r − 1)-chain deﬁned by

∂

≡



i=0

(−1)

( p

... ˆp

...p

) (3.20)

where the point p

under ˆ is omitted. For example,

∂

( p

) = ( p

) − ( p

) + ( p

)

∂

( p

) = ( p

) − ( p

) + ( p

) − ( p

We formally deﬁne ∂

= 0forr = 0.

The operator ∂

acts linearly on an element c =



r,i

of C

(K ),

∂

c =



∂

r,i

. (3.21)

The RHS of (3.21) is an element of C

r−1

(K ). Accordingly, ∂

deﬁnes a map

∂

: C

(K ) → C

r−1

(K ). (3.22)

∂

is called the boundary operator. It is easy to see that the boundary operator

is a homomorphism.

Let K be an n-dimensional simplicial complex. There exists a sequence of

free Abelian groups and homomorphisms,

−→ C

(K )

∂

−→ C

n−1

(K )

∂

n−1

−→···

∂

−→ C

(K )

∂

−→ C

(K )

∂

−→ 0 (3.23)

where i : 0 → C

(K ) is an inclusion map (0 is regarded as the unit element

of C

(K )). This sequence is called the chain complex associated with K and

is denoted by C(K ). It is interesting to study the image and kernel of the

homomorphisms ∂

Deﬁnition 3.3. If c ∈ C

(K ) satisﬁes

∂

c = 0 (3.24)

c is called an r-cycle.Thesetofr -cycles Z

(K ) is a subgroup of C

(K ) and is

called the r-cycle group. Note that Z

(K ) = ker ∂

.[Remark:Ifr = 0, ∂

vanishes identically and Z

(K ) = C

(K ), see (3.23).]

Deﬁnition 3.4. Let K be an n-dimensional simplicial complex and let c ∈ C

(K ).

If there exists an element d ∈ C

r+1

(K ) such that

c = ∂

r+1

d (3.25)

then c is called an r-boundary.Thesetofr-boundaries B

(K ) is a subgroup

of C

(K ) and is called the r-boundary group. Note that B

(K ) = im ∂

r+1

[Remark: B

(K ) is deﬁned to be 0.]

From lemma 3.1, it follows that Z

(K ) and B

(K ) are subgroups of C

(K ).

We now prove an important relation between Z

(K ) and B

(K ), which is crucial

in the deﬁnition of homology groups.

Lemma 3.3. The composite map ∂

◦∂

r+1

: C

r+1

(K ) → C

r−1

(K ) is a zero map;

that is, ∂

(∂

r+1

c) = 0foranyc ∈ C

r+1

(K ).

Proof.Since∂

is a linear operator on C

(K ), it is sufﬁcient to prove the identity

∂

◦ ∂

r+1

= 0 for the generators of C

r+1

(K ).Ifr = 0, ∂

◦ ∂

= 0since∂

is a

zero operator. Let us assume r > 0. Take σ = ( p

...p

r+1

) ∈ C

r+1

(K ).We

ﬁnd

∂

(∂

r+1

σ) = ∂

r+1



i=0

(−1)

( p

... ˆp

...p

r+1

)

r+1



i=0

(−1)

∂

( p

... ˆp

...p

r+1

)

r+1



i=0

(−1)



i−1



j =0

(−1)

( p

... ˆp

...p

r+1

)

r+1



j =i+1

(−1)

j −1

( p

... ˆp

...p

r+1

)





j <i

(−1)

i+j

( p

... ˆp

...p

r+1

)

−



j >i

(−1)

i+j

( p

... ˆp

...p

r+1

) = 0 (3.26)

which proves the lemma.

Theorem 3.3. Let Z

(K ) and B

(K ) be the r -cycle group and the r-boundary

group of C

(K ),then

(K ) ⊂ Z

(K )(⊂C

(K )). (3.27)

Proof. This is obvious from lemma 3.3. Any element c of B

(K ) is written as

c = ∂

r+1

d for some d ∈ C

r+1

(K ). Then we ﬁnd ∂

c = ∂

(∂

r+1

d) = 0, that is,

c ∈ Z

(K ). This implies Z

(K ) ⊃ B

(K ).

What are the geometrical pictures of r -cycles and r -boundaries? With our

deﬁnitions, ∂

picks up the boundary of an r-chain. If c is an r -cycle, ∂

c = 0 tells

us that c has no boundary. If c = ∂

r+1

d is an r-boundary, c is the boundary of d

whose dimension is higher than c by one. Our intuition tells us that a boundary

has no boundary, hence Z

(K ) ⊃ B

(K ). Those elements of Z

(K ) that are not

boundaries play the central role in this chapter.

3.3.3 Homology groups

So far we have deﬁned three groups C

(K ), Z

(K ) and B

(K ) associated with

a simplicial complex K . How are they related to topological properties of K or

to the topological space whose triangulation is K ? Is it possible for C

(K ) to

express any property which is conserved under homeomorphism? We all know

that the edges of a triangle and those of a square are homeomorphic to each other.

What about their chain groups? For example, the 1-chain group associated with a

triangle is

) ={i( p

) + j ( p

) + k( p

)|i, j, k ∈ }

∼

⊕ ⊕

while that associated with a square is

)

∼

⊕ ⊕ ⊕ .

Clearly C

) is not isomorphic to C

), hence C

(K ) cannot be a candidate

of a topological invariant. The same is true for Z

(K ) and B

(K ). It turns out

that the homology groups deﬁned in the following provide the desired topological

invariants.

Deﬁnition 3.5. Let K be an n-dimensional simplicial complex. The rth

homology group H

(K ),0≤ r ≤ n, associated with K is deﬁned by

(K ) ≡ Z

(K )/B

(K ). (3.28)

[Remarks: If necessary, we deﬁne H

(K ) = 0forr > n or r < 0. If we

want to stress that the group structure is deﬁned with integer coefﬁcients, we

write H

(K ; ). We may also deﬁne the homology groups with -coefﬁcients,

(K ; ) or those with

-coefﬁcients, H

(K ;

).]

Since B

(K ) is a subgroup of Z

(K ), H

(K ) is well deﬁned. The group

(K ) is the set of equivalence classes of r -cycles,

(K ) ≡{[z]|z ∈ Z

(K )} (3.29)

where each equivalence class [z] is called a homology class.Twor -cycles z and



are in the same equivalence class if and only if z −z



∈ B

(K ), in which case z

is said to be homologous to z



and denoted by z ∼ z



or [z]=[z



]. Geometrically

z − z



is a boundary of some space. By deﬁnition, any boundary b ∈ B

(K ) is

homologous to 0 since b −0 ∈ B

(K ). We accept the following theorem without

proof.

Theorem 3.4. Homology groups are topological invariants. Let X be

homeomorphic to Y and let (K, f ) and (L , g) be triangulations of X and Y

respectively. Then we have

(K )

∼

(L) r = 0, 1, 2,.... (3.30)

In particular, if (K, f ) and (L, g) are two triangulations of X ,then

(K )

∼

(L) r = 0, 1, 2,.... (3.31)

Accordingly, it makes sense to talk of homology groups of a topological

space X which is not necessarily a polyhedron but which is triangulable. For an

arbitrary triangulation (K , f ), H

(X ) is deﬁned to be

(X ) ≡ H

(K ) r = 0, 1, 2,.... (3.32)

Theorem 3.4 tells us that this is independent of the choice of the triangulation

(K, f ).

Example 3.6. Let K ={p

}. The 0-chain is C

(K ) ={ip

|i ∈ }

∼

. Clearly

(K ) = C

(K ) and B

(K ) ={0} (∂

= 0andp

cannot be a boundary of

anything). Thus

(K ) ≡ Z

(K )/B

(K ) = C

(K )

∼

. (3.33)

Exercise 3.1. Let K ={p

, p

} be a simplicial complex consisting of two 0-

simplexes. Show that

(K ) =



⊕ (r = 0)

{0} (r = 0).

(3.34)

Example 3.7. Let K ={p

, p

,(p

)}.Wehave

(K ) ={ip

+ jp

|i, j ∈ }

(K ) ={k( p

)|k ∈ }.

Since ( p

) is not a boundary of any simplex in K , B

(K ) ={0} and

(K ) = Z

(K )/B

(K ) = Z

(K ).

If z = m( p

) ∈ Z

(K ), it satisﬁes

∂

z = m∂

( p

) = m{p

− p

}=mp

− mp

= 0.

Thus, m has to vanish and Z

(K ) = 0, hence

(K ) = 0. (3.35)

As for H

(K ),wehaveZ

(K ) = C

(K ) ={ip

+ jp

} and

(K ) = im ∂

={∂

i( p

)|i ∈ }={i ( p

− p

)|i ∈ }.

Deﬁne a surjective (onto) homomorphism f : Z

(K ) → by

f (ip

+ jp

) = i + j.

Then we ﬁnd

ker f = f

−1

(0) = B

(K ).

Theorem 3.1 states that Z

(K )/ ker f

∼

im f = ,or

(K ) = Z

(K )/B

(K )

∼

. (3.36)

Example 3.8. Let K ={p

, p

,(p

), ( p

)}, see ﬁgure 3.7(b).

This is a triangulation of S

. Since there are no 2-simplexes in K ,wehave

(K ) = 0andH

(K ) = Z

(K )/B

(K ) = Z

(K ).Letz = i (p

) +

j ( p

) + k( p

) ∈ Z

(K ) where i, j, k ∈ . We require that

∂

z = i( p

− p

) + j ( p

− p

) + k( p

− p

)

= (k − i) p

+ (i − j) p

+ ( j − k) p

= 0.

This is satisﬁed only when i = j = k. Thus, we ﬁnd that

(K ) ={i{( p

) + ( p

)}|i ∈ }.

This shows that Z

(K ) is isomorphic to and

(K ) = Z

(K )

∼

. (3.37)

Let us compute H

(K ).WehaveZ

(K ) = C

(K ) and

(K ) ={∂

[l( p

) + m( p

) + n( p

)]|l, m, n ∈ }

={(n − l) p

+ (l − m) p

+ (m − n) p

|l, m, n ∈ }.

Deﬁne a surjective homomorphism f : Z

(K ) → by

f (ip

+ jp

+ kp

) = i + j + k.

We verify that

ker f = f

−1

(0) = B

(K ).

From theorem 3.1 we ﬁnd Z

(K )/ ker f

∼

im f = ,or

(K ) = Z

(K )/B

(K )

∼

. (3.38)

K is a triangulation of a circle S

, and (3.37) and (3.38) are the homology

groups of S

Exercise 3.2. Let K ={p

, p

,(p

), ( p

)} be a

simplicial complex whose polyhedron is a square. Verify that the homology

groups are the same as those of example 3.8 above.

Example 3.9. Let K ={p

, p

,(p

), ( p

)};see

ﬁgure 3.6(b). Since the structure of 0-simplexes and 1-simplexes is the same

as that of example 3.8, we have

(K )

∼

. (3.39)

Let us compute H

(K ) = Z

(K )/B

(K ). From the previous example, we

have

(K ) ={i{( p

) + ( p

)}|i ∈ }.

Let c = m( p

) ∈ C

(K ).Ifb = ∂

c ∈ B

(K ),wehave

b = m{( p

) − ( p

) + ( p

)}

= m{( p

) + ( p

)} m ∈ .

This shows that Z

(K )

∼

(K ), hence

(K ) = Z

(K )/B

(K )

∼

{0}. (3.40)

Since there are no 3-simplexes in K ,wehaveB

(K ) ={0}.Then

(K ) = Z

(K )/B

(K ) = Z

(K ).Letz = m( p

) ∈ Z

(K ).Since

∂

z = m{( p

) − (p

) + (p

)}=0, m must vanish. Hence, Z

(K ) ={0}

and we have

(K )

∼

{0}. (3.41)

Exercise 3.3. Let

K ={p

, p

,(p

), ( p

( p

), ( p

)}

be a simplicial complex whose polyhedron is the surface of a tetrahedron. Verify

that

(K )

∼

(K )

∼

{0} H

(K )

∼

. (3.42)

K is a triangulation of the sphere S

and (3.42) gives the homology groups of S

3.3.4 Computation of H

(K)

Examples 3.6–3.9 and exercises 3.2, 3.3 share the same zeroth homology group,

(K )

∼

. What is common to these simplicial complexes? We have the

following answer.

Theorem 3.5. Let K be a connected simplicial complex. Then

(K )

∼

. (3.43)

Proof.SinceK is connected, for any pair of 0-simplexes p

and p

, there exists

a sequence of 1-simplexes ( p

), ( p

),...,(p

) such that ∂

(( p

) +

( p

) +···+( p

)) = p

− p

. Then it follows that p

is homologous

to p

, namely [p

]=[p

]. Thus, any 0-simplex in K is homologous to p

say.

Suppose

z =



i=1

∈ Z

(K )

where I

is the number of 0-simplexes in K . Then the homology class [z] is

generated by a single point,

[z]=









It is clear that [z]=0, namely z ∈ B

(K ),if



= 0.

Let σ

= ( p

j,1

j,2

)(1 ≤ j ≤ I

) be 1-simplexes in K , I

being the number

of 1-simplexes in K ,then

(K ) = im ∂

={∂

+···+n

)|n

,...,n

∈ }

={n

( p

1,2

− p

1,1

) +···+n

( p

− p

)|n

,...,n

∈ }.

Note that n

(1 ≤ j ≤ I

) always appears as a pair +n

and −n

in an element

of B

(K ). Thus, if

z =



∈ B

(K ) then



= 0.

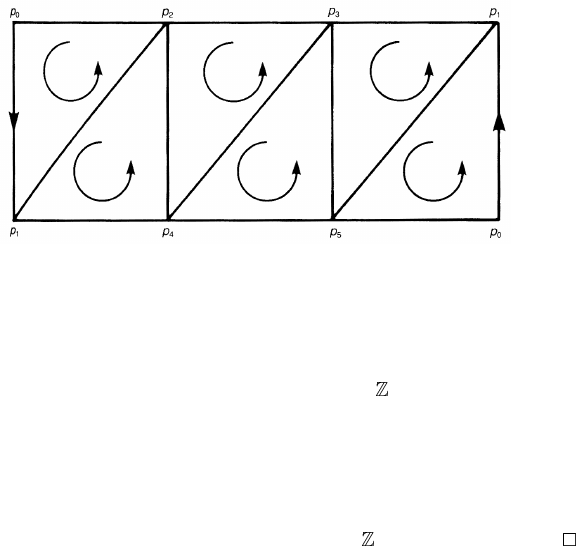
Figure 3.8. A triangulation of the M¨obius strip.

Now we have proved for a connected complex K that z =



∈ B

(K ) if

and only if



= 0.

Deﬁne a surjective homomorphism f : Z

(K ) → by

f (n

+···+n

) =



i=1

We then have ker f = f

−1

(0) = B

(K ). It follows from theorem 3.1 that

(K ) = Z

(K )/B

(K ) = Z

(K )/ ker f

∼

im f = .

3.3.5 More homology computations

Example 3.10. This and the next example deal with homology groups of non-

orientable spaces. Figure 3.8 is a triangulation of the M¨obius strip. Clearly

(K ) = 0. Let us take a cycle z ∈ Z

(K ),

z = i( p

) + j ( p

) + k( p

)

+l( p

) + m( p

) + n( p

z satisﬁes

∂

z = i {(p

) − ( p

) + ( p

)}

+ j{( p

) − ( p

) + ( p

)}

+ k{( p

) − ( p

) + ( p

)}

+l{( p

) − ( p

) + ( p

)}

+ m{( p

) − ( p

) + ( p

)}

+ n{( p

) − ( p

) + ( p

)}=0.

Since each of ( p

), ( p

) and ( p

) appears once

and only once in ∂

z, all the coefﬁcients must vanish, i = j = k = l = m = n =