Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


Now the expansion of S[x ] around x = x
c
takes the form
S[x
c
+ y]=S[x
c
]+
1
2!
dt
1
dt
2
y(t
1
)y(t
2
)
δ
2
S[x ]
δx(t
1
)δx(t
2
)
x=x
c
(1.136)
where y(t) satisfies the boundary condition y(t
i
) = y(t
f
) = 0. Note that (1) the
first-order term vanishes since δS[x]/δx = 0atx = x
c
and (2) terms of order
three and higher do not exist since the action is second order in x. Therefore, this
expansion is exact and this problem is exactly solvable as we see later.
By noting that
δ
δx(t
1
)
t
f
t
i
dt
1
2
m ˙x (t)
2
−
1
2
mω
2
x(t)
2
=−m
d
2
dt
2
1
x(t
1
) − mω
2
x(t
1
)
=−m
d
2
dt
2
1
+ ω
2
x(t
1
)
and that
δx(t
1
)
δx(t
2
)
= δ(t
1
− t
2
)
we obtain the second-order functional derivative
δ
2
S[x ]
δx(t
1
)δx(t
2
)
=−m
d
2
dt
2
1
+ ω
2
δ(t
1
− t
2
). (1.137)
Substituting this into equation (1.136) we find that
S[x
c
+ y]=S[x
c
]−
m
2!
dt
1
dt
2
y(t
1
)y(t
2
)
d
2
dt
2
1
+ ω
2
δ(t
1
− t
2
)
= S[x
c
]+
m
2
dt ( ˙y
2
− ω
2
y
2
), (1.138)
where the boundary condition y(t
i
) = y(t
f
) = 0 has been taken into account.
Since
x is translationally invariant,
14
we may replace x by y to obtain
x
f
, t
f
|x
i
, t
i
=e
iS[x
c
]
y(t
i
)=y(t
f
)=0
y e
i
m
2
t
f
t
i
dt ( ˙y
2
−ω
2
y
2
)
. (1.139)
Let us evaluate the fluctuation part
I
f
=
y(0)=y(T )=0
y e
i
m
2
T
0
dt ( ˙y
2
−ω
2
y
2
)
(1.140)
14
Integrating over all possible paths x(t) with x(t
i
) = x
i
and x(t
f
) = x
f
is equivalent to integrating
over all possible paths y(t) with y(t
i
) = y(t
f
) = 0, where x(t) = x
c
(t) + y(t).
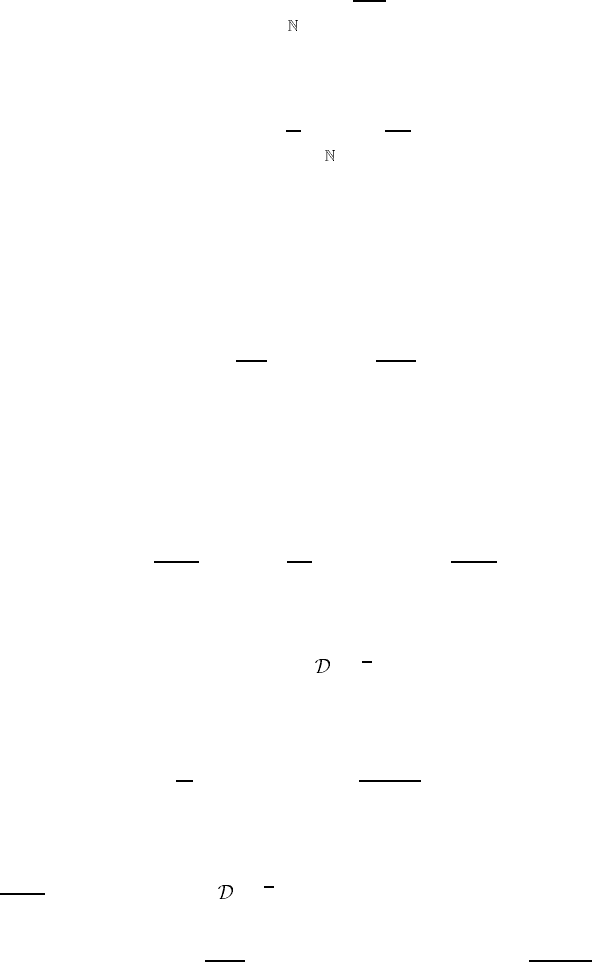
where we have shifted the t variable so that t
i
now becomes t = 0. We expand
y(t) as
y(t) =
n∈
a
n
sin
nπ t
T
(1.141)
in conformity with the boundary condition. Substitution of this expansion into the
integral in the exponent yields
T
0
dt ( ˙y
2
− ω
2
y
2
) =
T
2
n∈
a
2
n
nπ
T
2
− ω
2
.
The Fourier transform from y(t) to {a
n
} may be regarded as a change of variables
in the integration. For this transformation to be well defined, the number of
variables must be the same. Suppose the number of the time slice is N + 1,
including t = 0andt = T , for which there are N − 1 independent y
k
.
Correspondingly, we must put a
n
= 0forn > N − 1. The Jacobian associated
with this change of variables is
J
N
= det
∂y
k
∂a
n
= det
sin
nπ t
k
T
(1.142)
where t
k
is the kth time step when [0, T ] is divided into N infinitesimal steps.
This Jacobian can be evaluated most easily for a free particle. Since the
transformation {y
k
}→{a
n
} is independent of the potential, the Jacobian should
be identical for both cases. The probability amplitude for a free particle has been
obtained in (1.104) leading to
x
f
, T |x
i
, 0=
1
2πiT
1/2
exp
i
m
2T
(x
f
− x
i
)
2
=
1
2πiT
1/2
e
iS[x
c
]
.
(1.143)
This is written in terms of a path integral as
e
iS[x
c
]
y(0)=y(T )=0
y e
i
m
2
T
0
dt ˙y
2
. (1.144)
By comparing these two expressions and noting that
m
2
T
0
dt ˙y
2
→ m
N
n=1
a
2
n
n
2
π
2
4T
we arrive at the equality
1
2πiT
1/2
=
y(0)=y(T )=0
y e
i
m
2
T
0
dt ˙y
2
= lim
N→∞
J
N
1
2πiε
1/2
da
1
...da
N−1
exp
im
N−1
n=1
a
2
n
π
2
n
2
4T
.
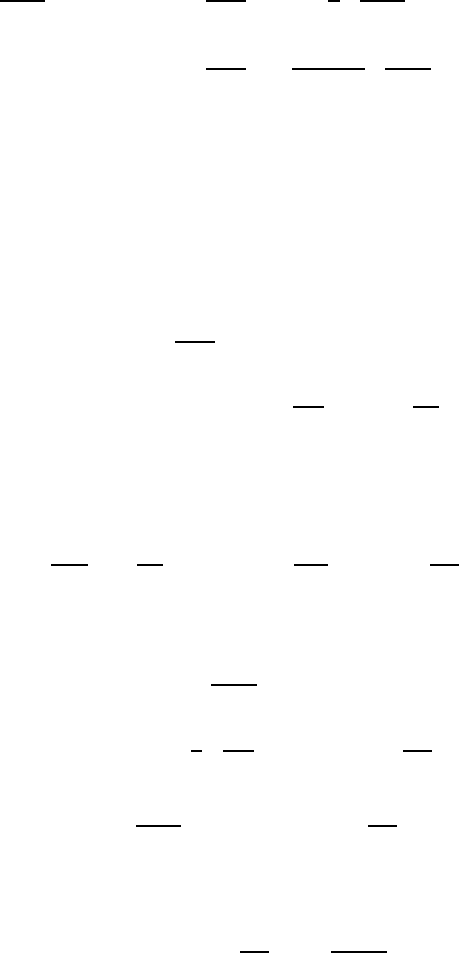
By carrying out the Gaussian integrals, it is found that
1
2πiT
1/2
= lim
N→∞
J
N
1
2πiε
N/2
N−1
n=1
1
n
4πiT
π
2
1/2
= lim
N→∞
J
N
1
2πiε
N/2
1
(N − 1)!
4πiT
π
2
(N−1)/2
from which we finally obtain, for finite N,that
J
N
= N
−N/2
2
−(N −1)/2
π
N−1
(N − 1)!. (1.145)
The Jacobian J
N
clearly diverges as N →∞. This does not matter at all,
however, since we are not interested in J
N
on its own but a combination with
other (divergent) factors.
The transition amplitude of a harmonic oscillator is now given by
x
f
, T |x
i
, 0= lim
N→∞
J
N
1
2πiε
N/2
e
iS[x
c
]
×
da
1
...da
N−1
exp
i
mT
4
N−1
n=1
a
2
n
nπ
T
2
− ω
2
.
(1.146)
The integrals over a
n
are simple Gaussian integrals and easily carried out to yield
da
n
exp
imT
4
a
2
n
nπ
T
2
− ω
2
=
4iT
πn
2
1/2
1 −
ωT
nπ
2
−1/2
.
By substituting this result into equation (1.146), we obtain
x
f
, t
f
|x
i
, t
i
= lim
N→∞
J
N
N
2πiT
N/2
e
iS[x
c
]
×
N−1
k=1
1
k
4iT
π
1/2
N−1
n=1
1 −
ωT
nπ
2
−1/2
=
1
2πiT
1/2
e
iS[x
c
]
N−1
n=1
1 −
ωT
nπ
2
−1/2
. (1.147)
The infinite product over n is well known and reduces to
lim
N→∞
N
n=1
1 −
ωT
nπ
2
=
sin ωT
ωT
(1.148)
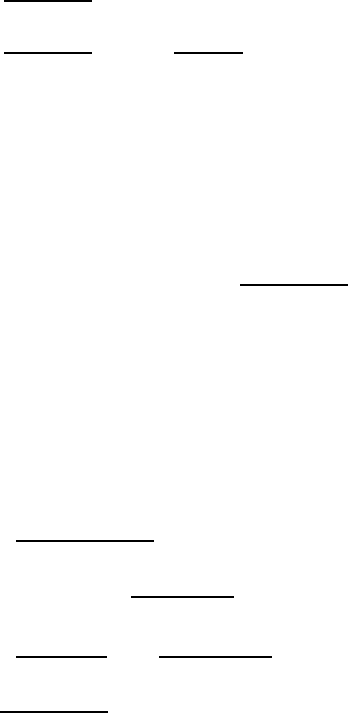
Note that the divergence of J
N
cancelled with the divergence of the other terms
to yield a finite value. Finally we have shown that
x
f
, t
f
|x
i
, t
i
=
ω
2πisinωT
1/2
e
iS[x
c
]
=
ω
2πisinωT
1/2
exp
iω
2sinωT
{(x
2
f
+ x
2
i
) cos ωT − 2x
i
x
f
}
.
(1.149)
1.4.2 Partition function
The partition function of a harmonic oscillator is easily obtained from the
eigenvalue E
n
= (n + 1/2)ω,
Tr e
−β
ˆ
H
=
∞
n=0
e
−β(n+1/2)ω
=
1
2sinh(βω/2)
. (1.150)
The inverse temperature β can be regarded as the imaginary time by putting
iT = β. Then the partition function may be evaluated from the path integral
point of view.
Method 1: The trace may be taken over {|x } to yield
Z(β) =
dx x|e
−β
ˆ
H
|x
=
ω
2πi(−isinhβω)
1/2
×
dx exp i
ω
−2i sinh βω
(2x
2
cosh βω − 2x
2
)
=
ω
2π sinh βω
1/2
π
ω tanh(βω/2)
1/2
=
1
2sinh(βω/2)
(1.151)
where use has been made of equation (1.149).
The following exercise serves as a preliminary to Method 2.
Exercise 1.5. (1) Let A be a symmetric positive-definite n × n matrix. Show that
dx
1
...dx
n
exp
−
i, j
x
i
A
ij
x
j
= π
n/2
(det A)
−1/2
= π
n/2
i
λ
−1/2
i
(1.152)
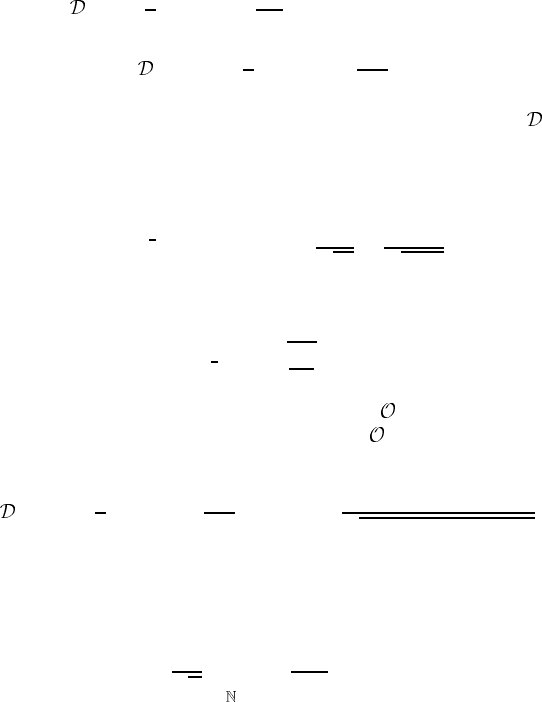
where λ
i
is the eigenvalue of A.
(2) Let A be a positive-definite n × n Hermite matrix. Show that
dz
1
d¯z
1
...dz
n
d¯z
n
exp
−
i, j
¯z
i
A
ij
z
j
= π
n
(det A)
−1
= π
n
i
λ
−1
i
.
(1.153)
Method 2: We next obtain the partition function by evaluating the path
integral over the fluctuations with the help of the functional determinant and the
ζ -function regularization. We introduce the imaginary time τ = it and rewrite
the path integral as
y(0)=y(T )=0
y exp
i
2
dty
−
d
2
dt
2
− ω
2
y
→
y(0)=y(β)=0
¯
y exp
−
1
2
dτ y
−
d
2
dτ
2
+ ω
2
y
,
where we noted the boundary condition y(0) = y(β) = 0. Here the bar on
implies the path integration measure with imaginary time.
Let A be an n × n Hermitian matrix with positive-definite eigenvalues
λ
k
(1 ≤ k ≤ n). Then for real variables x
k
, we obtain from exercise 1.5 that
n
k=1
∞
−∞
dx
k
e
−
1
2
p,q
x
p
A
pq
x
q
=
n
k=1
1
√
λ
k
=
1
√
det A
where we neglected numerical factors. This is a generalization of the well-known
Gaussian integral
∞
−∞
dxe
−
1
2
λx
2
=
2π
λ
for λ>0. We define the determinant of an operator
by the (properly
regularized) infinite product of its eigenvalues λ
k
as Det =
k
λ
k
.
15
Then
the previous path integral is written as
y(0)=y(β)=0
¯
y exp
−
1
2
dτ y
−
d
2
dτ
2
+ω
2
y
=
1
Det
D
(−d
2
/dτ
2
+ ω
2
)
,
(1.154)
where the subscript ‘D’ implies that the eigenvalues are evaluated with the
Dirichlet boundary condition y(0) = y(β) = 0.
The general solution y(τ ) satisfying the boundary condition is written as
y(τ ) =
1
√
β
n∈
y
n
sin
nπτ
β
. (1.155)
15
We will use ‘det’ for the determinant of a finite dimensional matrix while ‘Det’ for the (formal)
determinant of an operator throughout this book. Similarly, the trace of a finite-dimensional matrix is
denoted ‘tr’ while that of an operator is denoted ‘Tr’.
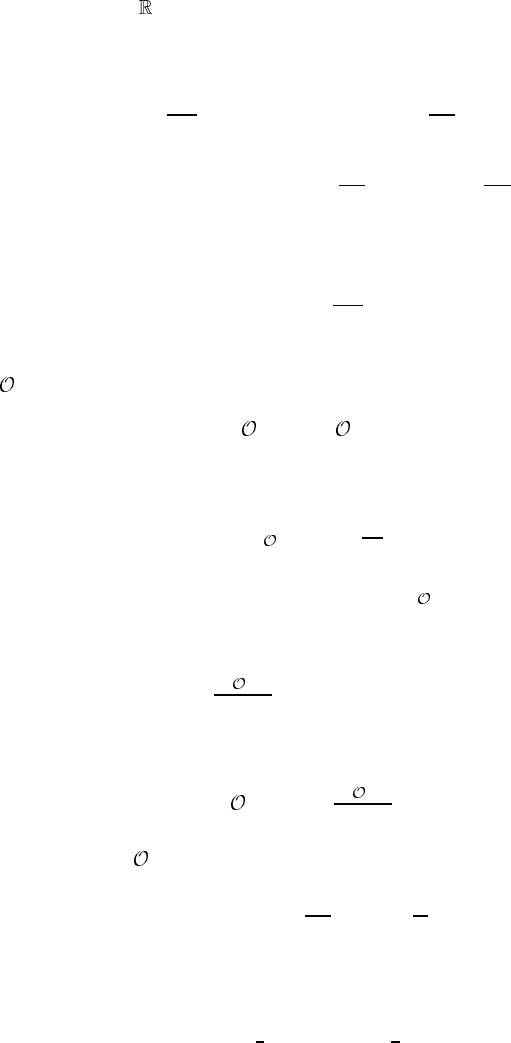
Note that y
n
∈ since y(τ ) is a real function. Since the eigenvalue of the
eigenfunction sin(nπτ/β) is λ
n
= (nπ/β)
2
+ ω
2
, the functional determinant
is formally written as
Det
D
−
d
2
dτ
2
+ ω
2
=
∞
n=1
λ
n
=
∞
n=1
nπ
β
2
+ ω
2
=
∞
n=1
nπ
β
2
∞
p=1
1 +
βω
pπ
2
. (1.156)
The first infinite product in the last line is written as
Det
D
−
d
2
dτ
2
.
We will evaluate this infinite product through the ζ -function regularization. Let
be an operator with positive-definite eigenvalues λ
n
.Thenwehaveformally
log Det
= Tr log =
n
log λ
n
. (1.157)
Now we define the spectral ζ -function as
ζ
(s) ≡
n
1
λ
s
n
. (1.158)
The RHS converges for sufficiently large Re s and ζ
(s) is analytic with respect
to s in this region. Moreover, it can be analytically continued to the whole s-plane
except at a possible finite number of points. By noting that
dζ
(s)
ds
s=0
=−
n
log λ
n
we arrive at the expression
Det
= exp
−
dζ
(s)
ds
s=0
. (1.159)
We replace
by −d
2
/dτ
2
in the case at hand to find
ζ
−d
2
/dτ
2
(s) =
n≥1
nπ
β
−2s
=
β
π
2s
ζ(2s) (1.160)
where ζ(2s) is the celebrated Riemann ζ -function. It is analytic over the whole
s-plane except at the simple pole at s = 1. From the well-known values
ζ(0) =−
1
2
ζ
(0) =−
1
2
log(2π) (1.161)

we obtain
ζ
−d
2
/dτ
2
(0) = 2log
β
π
ζ(0) + 2ζ
(0) =−log(2β).
We have finally shown that
Det
D
−
d
2
dτ
2
= e
log(2β)
= 2β (1.162)
and that
Det
D
−
d
2
dτ
2
+ ω
2
= 2β
∞
p=1
1 +
βω
pπ
2
. (1.163)
The infinite product in this equation is well known but let us pretend that we are
ignorant about this product.
The partition function is now expressed as
Tr e
−β H
=
2β
∞
p=1
1 +
βπ
pπ
2
−1/2
π
ω tanh(βω/2)
1/2
. (1.164)
By comparing this with the result (1.151), we have proved the formula
∞
n=1
1 +
βω
nπ
2
=
π
βω
sinh(βω)
namely
∞
n=1
1 +
x
2
n
2
=
sinh(π x)
π x
. (1.165)
What about the infinite product expansion of the cosh function? This is given
by using the path integral with respect to the fermion, which we will work out in
the next section.
1.5 Path integral quantization of a Fermi particle
The particles observed in Nature are not necessarily Bose particles whose position
and momentum operators obey the commutation relation [p, x]=−i. There are
particles called fermions whose operators satisfy anti-commutation relations. A
classical description of a fermion requires anti-commuting numbers called the
Grassmann numbers.

1.5.1 Fermionic harmonic oscillator
The bosonic harmonic oscillator in the previous section is described by the
Hamiltonian
16
H =
1
2
(a
†
a + aa
†
)
where a and a
†
satisfy the commutation relations
[a, a
†
]=1 [a, a]=[a
†
, a
†
]=0.
The Hamiltonian has eigenvalues (n + 1/2)ω (n ∈
) with the eigenvector |n:
H |n=(n +
1
2
)ω|n.
Now suppose there is a Hamiltonian
H =
1
2
(c
†
c − cc
†
)ω. (1.166)
This is called the fermionic harmonic oscillator, which may be regarded as
a Fourier component of the Dirac Hamiltonian, which describes relativistic
fermions. If the operators c and c
†
should satisfy the same commutation relations
as those satisfied by bosons, the Hamiltonian would be a constant H =−ω/2.
Suppose, in contrast, they satisfy the anti-commutation relations
{c, c
†
}≡cc
†
+ c
†
c = 1 {c, c}={c
†
, c
†
}=0. (1.167)
The Hamiltonian takes the form
H =
1
2
[c
†
c − (1 −cc
†
)]ω = (N −
1
2
)ω (1.168)
where N = c
†
c. It is easy to see that the eigenvalue of N must be either 0 or 1.
In fact, N satisfies N
2
= c
†
cc
†
c = N, namely N(N − 1) = 0. This is nothing
other than the Pauli principle.
Let us study the Hilbert space of the Hamiltonian H .Let|n be an
eigenvector of H with the eigenvalue n,wheren = 0, 1 as shown earlier. It
is easy to verify the following relations;
H |0=−
ω
2
|0 H |1=
ω
2
|1
c
†
|0=|1 c|0=0 c
†
|1=0 c|1=|0.
It is convenient to introduce the component expressions
|0=
0
1
|1=
1
0
.
16
We will drop ˆon operators from now on unless this may cause confusion.

Exercise 1.6. Suppose the basis vectors have this form. Show that the operators
have the following matrix representations
c =
00
10
, c
†
=
01
00
,
N =
10
00
, H =
ω
2
10
0 −1
.
The commutation relation [x , p]=i for a boson has been replaced by
[x, p]=0 in the path integral formalism of a boson. For a fermion, the anti-
commutation relation {c, c
†
}=1 should be replaced by {θ,θ
∗
}=0, where θ and
θ
∗
are anti-commuting classical numbers called Grassmann numbers.
1.5.2 Calculus of Grassmann numbers
To distinguish anti-commuting Grassmann numbers from commuting real and
complex numbers, the latter will be called the ‘c-number’, where c stands for
commuting. Let n generators {θ
1
,...,θ
n
} satisfy the anti-commutation relations
{θ
i
,θ
j
}=0 ∀i, j. (1.169)
Then the set of the linear combinations of {θ
i
} with the c-number coefficients is
called the Grassmann number and the algebra generated by {θ
i
} is called the
Grassmann algebra, denoted by
n
. An arbitrary element f of
n
is expanded
as
f (θ) = f
0
+
n
i=1
f
i
θ
i
+
i< j
f
ij
θ
i
θ
j
+···
=
0≤k≤n
1
k!
{i}
f
i
1
,...i
k
θ
i
1
...θ
i
k
, (1.170)
where f
0
, f
i
, f
ij
,...and f
i
1
,...,i
k
are c-numbers that are anti-symmetric under the
exchange of any two indices. The element f is also written as
f (θ ) =
k
i
=0,1
˜
f
k
1
,...,k
n
θ
k
1
1
...θ
k
n
n
. (1.171)
Take n = 2 for example. Then
f (θ ) = f
0
+ f
1
θ
1
+ f
2
θ
2
+ f
12
θ
1
θ
2
=
˜
f
00
+
˜
f
10
θ
1
+
˜
f
01
θ
2
+
˜
f
11
θ
1
θ
2
.
The subset of λ
n
which is generated by monomials of even (resp. odd) power in
θ
k
is denoted by
n
+
(
n
−
):
n
=
n
+
⊕
n
−
. (1.172)

The separation of
n
into these two subspaces is called
2
-grading. We call an
element of
n
+
(
n
−
) G-even (G-odd). Note that dim λ
n
= 2
n
while dim
n
+
=
dim
n
−
= 2
(n−1)
.
The generator θ
k
does not have a magnitude and hence the set of Grassmann
numbers is not an ordered set. Zero is the only number that is a c-number as well
as a Grassmann number simultaneously. A Grassmann number commutes with a
c-number. It should be clear that the generators satisfy the following relations:
θ
2
k
= 0
θ
k
1
θ
k
2
...θ
k
n
= ε
k
1
k
2
...k
n
θ
1
θ
2
...θ
n
(1.173)
θ
k
1
θ
k
2
...θ
k
m
= 0 (m > n),
where
ε
k
1
...k
n
=
+1if{k
1
...k
n
} is an even permutation of {1 ...n}
−1if{k
1
...k
n
} is an odd permutation of {1 ...n}
0otherwise.
A function of Grassmann numbers is defined as a Taylor expansion of the
function. When n = 1, for example, we have
e
θ
= 1 +θ
since higher-order terms in θ vanish identically.
1.5.3 Differentiation
It is assumed that the differential operator acts on a function from the left:
∂θ
j
∂θ
i
=
∂
∂θ
i
θ
j
= δ
ij
. (1.174)
It is also assumed that the differential operator anti-commutes with θ
k
.The
Leibnitz rule then takes the form
∂
∂θ
i
(θ
j
θ
k
) =
∂θ
j
∂θ
i
θ
k
− θ
j
∂θ
k
∂θ
i
= δ
ij
θ
k
− δ
ik
θ
j
. (1.175)
Exercise 1.7. Show that
∂
∂θ
i
∂
∂θ
j
+
∂
∂θ
j
∂
∂θ
i
= 0. (1.176)
It is easily shown from this exercise that the differential operator is nilpotent
∂
2
∂θ
2
i
= 0. (1.177)
Exercise 1.8. Show that
∂
∂θ
i
θ
j
+ θ
j
∂
∂θ
i
= δ
ij
. (1.178)
