Мустафин М.А. Энергосберегающие системы электропривода центробежных насосных агрегатов. Автореферат
Подождите немного. Документ загружается.


Рисунок 10 – Расчет энергетических показателей привода ЦН с МДП.
2. Определяются токи статора и ротора АД, коэффициент сдвига
статора К
С1
и ротора К
С2
, активные и реактивные мощности статора Р
1АД
,
Q
1АД
и ротора Р
2
, Q
2
. Здесь должны быть рассмотрены электромагнитные
процессы в АД в режиме двойного питания, соответствующем п.1.
3. Активная мощность на входе НПЧ Р
1НПЧ
соответствует, за вычетом
потерь в преобразователе, активной мощности ротора Р
2
, реактивная
мощность Q
1НПЧ
определяется по рассчитанным Р
2
, Q
2
, К
С2
и функциям
регулирования МДП.
4. Определяется суммарная мощность, потребляемая приводом
Р
МДП
=
Р
1АД
±
Р
1НПЧ
; Q
МДП
= Q
1АД
+ Q
1НПЧ
; S
МДП
=
22
МДПМДП
QP
+
(9)
и по (9) - коэффициент сдвига (коэффициент мощности по первым
гармоническим) привода в целом
МДП
МДП
СМДП
S
Р
К
=
. (10)
Ниже (рисунок 11) представлены результаты, полученные на
разработанной модели. Наибольшую реактивную мощность привод
потребляет при регулировании по минимуму реактивной мощности ротора,
что объясняется тем, что для создания одного и того же магнитного потока со
стороны статора требуется большая реактивная мощность, чем со стороны
статора (частота скольжения
S
f
значительно меньше частоты сети
1
f
).
21
Расчет U
2
, δ, токов АД, – подпрограмма “Matrix”
(рис.2.4, 2.6)
Расчет Q
1AD
,P
1AD
,S
1AD
,K
cAD1
,Q
2AD
,P
2AD
,S
2AD
Параметры НПЧ
Расчет Q
1НПЧ
, P
1НПЧ
, S
1НПЧ
, K
cНПЧ1
Расчет Q
МДП
, P
МДП
, S
МДП
, K
cМДП
Вывод результатов
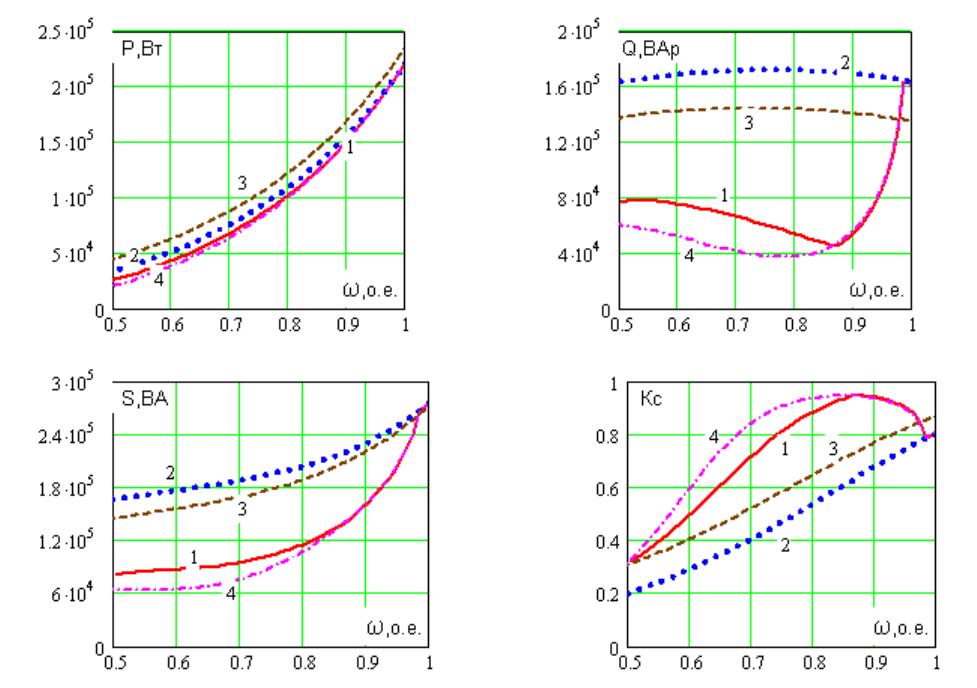
1 –
Q1
=0
; 2
–
Q2
=0
; 3
–
ΔP
– min; 4 – I2 =I2н.
Рисунок 11 – Составляющие суммарной мощности и коэффициент сдвига
привода центробежного насоса с машиной двойного питания (Нс = 0).
При регулировании по Q1=0 реактивная мощность, потребляемая при
пониженной подаче, снижается на 67%, если использовать закон I2 =I2н – на
82%. Суммарная активная мощность, потребляемая приводом, практически
не зависит от закона регулирования МДП и определяется нагрузкой.
Некоторое снижение потерь в АД приводит к уменьшению Р
Σ
при
регулировании по ΔP – min на 5.1% по сравнению с вариантом I2 =I2н, на
0.6% - с вариантом Q2=0 и на 3.1% - с вариантом Q1=0. Практически
одинаковыми энергетические показатели становятся при номинальной
подаче, что связано с ограничением токов номинальными значениями при
расчете функций регулирования в алгоритме “Matrix”.
На полученной модели выполнены численные исследования, позволившие
не только сравнить эффективность различных критериев оптимизации, но и
определить влияние на энергетику двигателя, преобразователя и привода в
целом таких параметров, как коэффициент трансформации трансформатора,
противодавление в трубопроводе, что позволяет определить основные
закономерности и пути снижения потерь в электроприводе ЦН.
В четвертом подразделе второго раздела исследуется
энергопотребление электроприводов ЦН в динамических режимах, которые
22
могут быть вызваны оперативными включениями или отключениями
отдельных элементов системы или изменением режимов их
функционирования.
Для оценки энергопотребления в переходных режимах работы
центробежных агрегатов разработана модель динамических процессов
асинхронного электропривода, рисунок 12. Созданная на базе
компьютерного математического приложения «Mathcad» модель является
универсальной, поскольку охватывает все варианты управления АД.
Рисунок 12 - Блок – схема алгоритма расчета динамических характеристик
привода центробежного насоса.
Путем задания необходимых начальных условий, моделируются все виды
переходных процессов (пуск, останов, реверс, сброс и наброс нагрузки),
различные формы задающих воздействий для их формирования. Модель
учитывает основные технические характеристики ЦН и трубопровода.
Вектор правых частей системы дифференциальных уравнений формируется
по данным о схеме электропривода, параметрах АД, характере нагрузки. Вид
переходного процесса и его параметры вместе с параметрами нагрузки
определяют вектор начальных условий. Кроме того, используя подпрограмму
«Расчет du/dt», можно задать форму и интенсивность нарастания управляющих
воздействий. Далее выбирается метод численного решения системы (Рунге-
Кутта с фиксированным или адаптированным шагом, Булириш-Штера и т.д.),
интервал и шаг решения. Вывод результатов осуществляется в табличном или
графическом виде.
В качестве примера ниже (рисунки 13, 14) приведены результаты расчета
электромагнитного момента и тока статора асинхронного двигателя 4АНК 315
23
Параметры АД.
Схема включения
Параметры насоса и
трубопровода:
Н
0
,Н
С
,η,С
Н
Вид и
параметры ПП
Расчет dM
C
/dt
Расчет du
1
/dt, du
2
/dt
Формирование
вектора правых
частей системы ДУ
Метод, интервал и
шаг решения
Формирование
вектора
начальных
условий
Решение системы ДУ
Вывод результатов
i, A
t, с
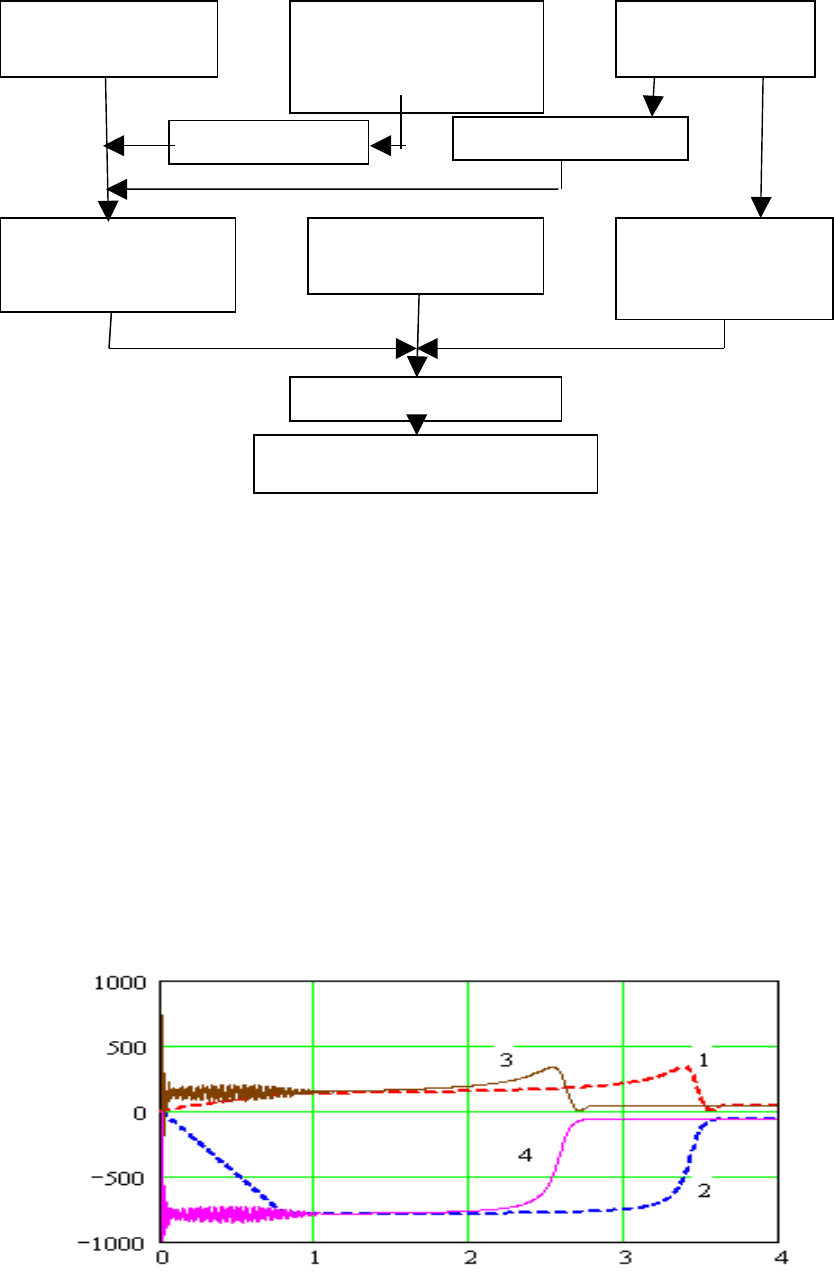
4У3 при прямом пуске насоса и при экспоненциальном нарастании напряжения
на статоре.
1,3 – активные составляющие; 2,4 – реактивные составляющие.
Рисунок 13 – Токи АД при прямом (3,4) и плавном (1,2) пуске с центробежной
нагрузкой.
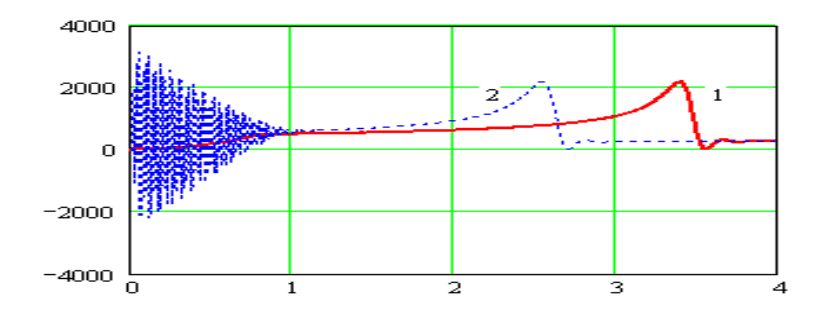
Рисунок 14 – Моменты АД при прямом (2) и плавном (1) пуске с центробежной
нагрузкой.
Отсутствие резких колебание электромагнитного момента при
регулируемом значении du/dt позволяет избежать резких гидравлических
перегрузок элементов насосного агрегата.
В результате на монитор в табличном или графическом виде выводятся:
- мгновенные значения проекций токов статора и ротора i
1x
(t), i
1y
(t), i
2x
(t),
i
2y
(t);
- мгновенные значения скорости вращения ротора АД ω(t);
- мгновенные значения момента сопротивления механизма М
С
(t) и
электромагнитного момента АД М(t);
- максимальные и минимальные значения указанных параметров.
Этих данных достаточно для того, чтобы, используя дополнительно
разработанный программный модуль «Расчет энергетических
характеристик», получить данные энергопотребления в динамических
режимах.
24
M, Нм
t, c

На рисунках 15, 16 представлены результаты расчетов мгновенных
значений потребляемой мощности асинхронного двигателя при прямом
пуске центробежного насоса и мгновенного коэффициента мощности
двигателя
)(
)(
)(
tS
tP
tK
M
=
. (11)
1 – активная Р(t); 2 – реактивная мощность Q(t); 3 – полная мощность S(t).
Рисунок 15 - Прямой пуск ЦН.
Рисунок 16 - Коэффициент мощности АД при прямом пуске ЦН.
Далее в программе рассчитываются мгновенное значение полезной
мощности на валу двигателя во время переходного процесса.
)()()( tMttP
ЭМВ
ω
=
. (12)
и мгновенный коэффициент полезного действия.
)(
)(
)(
tP
tP
t
В
=
η
. (13)
Кроме характера протекания электромагнитных и электромеханических
переходных процессов, при проектировании систем электропривода полезно
знать интегральные характеристики за все время, например, пуска. Эти
данные получаем путем интегрирования соответствующих переменных в
пределах времени протекания переходного процесса. Нами проведено
исследование влияния формы и интенсивности нарастания напряжения на
25

пусковые энергетические характеристики. Интегральные характеристики
приведены в таблице 1.
Таблица 1 – Интегральные характеристики при плавном пуске
Постоянная
времени Т, с
P
n
, кВт Q
n
, кВАр S
n
, кВА K
мп
η
n
0
570.7 2029 2133 0.267 0.396
0.1 602.2 2226 2334 0.259 0.348
0.2 688.4 2593 2719 0.254 0.330
0.5 980.1 4091 4265 0.230 0.219
Таким образом, предлагаемые методика и программа расчета
энергетических показателей позволяют оценить характер переходных
процессов и определить энергозатраты в динамических режимах различных
систем электропривода центробежных механизмов.
В третьем разделе диссертации исследуются энергетические
характеристики электроприводов при несинусоидальном питании.
Несинусоидальность выходного напряжения реальных
преобразователей частоты (ПЧ), применяемых в регулируемом
электроприводе, вызывает искажение токов, электромагнитного момента,
ухудшает использование элементов электропривода и его энергетические
характеристики. Высшие гармонические составляющие токов вызывают
добавочные потери в обмотках двигателя и трансформатора ПЧ,
увеличиваются потери на гистерезис и вихревые токи в стали. Кроме
отрицательных энергетических последствий, негативное влияние оказывается
на механическую часть насосных агрегатов. При определенных,
резонансных, соотношениях частот и амплитуд гармоник и собственных
частот насосного агрегата, в нем возникает нежелательная механическая
вибрация ротора. Это явление так же требует дополнительного изучения.
В первом подразделе третьего раздела определены задачи и проведен
анализ известных методов анализа приводов с несинусоидальным питанием.
Предложен метод исследования электромагнитных и электромеханических
процессов в асинхронных приводах с несинусоидальным питанием, который
является развитием методов гармонических составляющих и обобщенных
векторов. Каждая гармоническая составляющая напряжений и токов
представляется вектором с соответствующей амплитудой и частотой
вращения, что позволяет согласовать уравнения для них с уравнениями для
первых гармонических АД. Таким образом, совмещаются положения метода
гармонических составляющих и математическое описание обобщенной
электрической машины, использованное при расчете привода по первым
гармоническим.
Получено выражение для ν – х гармонических составляющих токов АД в
виде проекций на синхронные оси, позволяющая определить их мгновенные
значения:
26

ν
ν
ν
ν
ννννν
ννννν
ννννννν
ννννννν
ννν
ν
ν
ν
ωσω
ωσω
ωσωωσω
σωωσωω
σωω
y
x
y
x
srsmsmrs
rssmrsms
msmrsmrs
mrsmsrsm
rs
y
x
y
x
U
U
U
U
rlllsllrsllls
llsrllllsllrs
llrlllslrslsrl
lllsllrlsrllrs
lsrl
I
I
I
I
2
2
1
1
2
222
2
2
2
2
22
2
2
22
2
22222
2
2
2
22222
2
2
2
22222
2
2
2
2
1
1
)(
)(
)(
1
−−
−−
−+−
−−+
+
=
(14)
Таким образом, мы имеем возможность, зная гармонический состав
выходного напряжения выбранного (или проектируемого) ПЧ, определить
мгновенные значения токов в двигателе и в приводе в целом. Однако,
необходима и интегральная оценка влияния несинусоидальности питающего
напряжения на энергетические характеристики привода – КПД и
коэффициент мощности.
Ток статора при несинусоидальном питании можно представить как
сумму первой и высших гармонических составляющих:
∑
∞
=
+=
1
2
1
2
)1(11
2
ν
ν
I
II
, (15)
где I
1(1)
– действующее значение первой гармоники тока статора;
I
1ν
– амплитуда 2 – й гармоники тока статора.
Для интегральной оценки используем коэффициент искажения тока
статора, который равен отношению действующих значений первой
гармонической к полному току статора при несинусоидальном питании:
.
1
)1(1
1
I
I
k
u
=
(16)
Коэффициент полезного действия АД, при несинусоидальном питании
уменьшается из-за потерь, вызванных высшими гармоническими токов в
меди двигателя
ν
M
P
∆
:
+=∆
∑ ∑
∞
≠
∞
≠
1 1
2
22
2
11
2/2/3
ν ν
ννν
IrIrP
M
. (17)
Коэффициент мощности электропривода при несинусоидальном
питании определяется как
,
ИCM
kkk
⋅=
(18)
где k
С
= cosφ – коэффициент сдвига (коэффициент мощности по первым
гармоникам токов и напряжений) определяется во втором разделе.
Влияние высших гармоник на электромагнитный момент с
достаточной точностью можно определить по взаимодействию основного
потока с высшими гармоническими составляющими тока ротора. Расчет их
27

можно провести, учитывая только взаимодействие высших гармонических
токов с первыми гармониками
)(
2
3
2121
νν
yxxymПэм
iiiiLpM
−=
. (19)
В подразделе рассмотрены схемные решения и элементная база
преобразователей частоты, используемых для управления АД.
Во втором подразделе третьего раздела исследуются
электромагнитные и электромеханические процессы в электроприводе
центробежных насосов по схеме «ПЧ – АД» при питании от реальных
преобразователей. ПЧ со звеном постоянного тока, применяемые в таких
приводах, подразделяются на ПЧ с управляемым выпрямителем (ПЧ с УВ) и
ПЧ с широтно – импульсной модуляцией (ПЧ с ШИМ). Получены выражения
для выходного напряжения этих ПЧ, проведен его гармонический анализ.
Выходное напряжение ПЧ с УВ имеет простую прямоугольную или
ступенчатую форму и фиксированный спектральный состав. Напряжение ПЧ
с ШИМ сложно по гармоническому составу, который зависит от величины и
частоты выходного напряжения, несущей частоты и меняется в процессе
регулирования.
В работе предлагается математическая модель, позволяющая
реализовать оптимальное частотное управление приводом ЦН и исследовать
качество выходного напряжения ПЧ в зависимости от режима работы
насосного агрегата. Для этого используются возможности по реализации
численных методов расчета и математического моделирования
математического приложения «Mathcad» (MathSoft). В соответствии с
принципом работы ПЧ с ШИМ, определим пилообразное опорное
напряжение как
⋅=
2
)(
t
tgarctgktU
НЕС
HЕС
ω
, (20)
а модулирующую кривую как
.sin)( ttU
выхМОД
ωµ
=
(21)
В (20) ω
нес
может задаваться независимо или являться функцией ω
нес
=f(ω
вых
). Параметры модуляции μ, ω
вых
определяются, как
ном
опт
U
U
=
µ
,
цнсвых
ωωω
=
, (22)
где U
опт
– оптимальное, по минимуму потерь, напряжение,
определенное ранее;
ω
цн
– частота вращения рабочего колеса ЦН, о.е.
Выходное напряжение ПЧ описывается логической функцией
28

).()(,
)()(,
)(
tUtUifE
tUtUifE
tU
ОДHЕС
ОДHЕС
вых
Μ
Μ
≥−
<
=
(23)
На рисунке 17 представлены результаты моделирования ПЧ с ШИМ,
которые могут выводиться не только в графическом, но и в цифровом
табличном виде. Что позволяет использовать сигналы управления U
И
для
непосредственного управления вентильными группами ПЧ.
Рисунок 17 - Формирование выходного напряжения ПЧ с ШИМ.
Для оценки энергетических показателей, кроме мгновенных значений,
необходимо знать интегральные характеристики, то есть гармонический
состав кривой напряжения.
Аналитическое проведение гармонического анализа затруднено, так как
состав U
вых
зависит от схемы преобразователя, глубины модуляции,
соотношении несущей и выходной частот ПЧ. Математическое приложение
«Mathcad» располагает несколькими вариантами встроенных функций
прямого и обратного преобразований Фурье численными методами. Важным
является то, что исследуемая функция может быть представлена в виде
комбинации аналитических и логических операций, то есть, записана в
неявном виде. Не рассматривая детально разработанную программу,
представим результат спектрального анализа U
вых
ПЧ с ШИМ. (рисунок 18).
29
0
0
0
0

Расчет U
ОПТ
Расчет ω
вых
, μ по (3.31)
Параметры ПЧ – ω
нес
Формирование U
вых
по (3.29)…(3.32)
ω
необх
Гарм. анализ СУ ПЧ
Вывод результатов
Рисунок 18
-
Спектрограмма выходного напряжения ПЧ с ШИМ.
Корректность использованных программ можно оценить, применив
обратное преобразование Фурье, то есть синтезировав кривую выходного
напряжения ПЧ по рассчитанным коэффициентам. Полученные результаты
расчета подтверждают высокую точность примененных математических
средств.
Для обобщения описанных выше операций, нами предлагается
математическая модель для исследования ПЧ с ШИМ при оптимальном, по
минимуму потерь в двигателе, управлении ЦН (рисунок 19).
Рисунок 19 - Блок – схема модели.
Оптимальное значение напряжения рассчитывается для заданной частоты
вращения рабочего колеса насоса с учетом параметров АД. Далее
определяются значения выходной частоты ПЧ и глубина регулирования,
соответствующие минимальным потерям в АД в данном режиме работы ЦН.
Формирование кривой выходного напряжения осуществляется в
соответствии с рисунком 17 для конкретной схемы ПЧ и выбранной несущей
частоты. Полученные сигналы управления поступают на формирователь
импульсов коммутации вентильных групп ПЧ, а кривая мгновенных
30
