Мустафин М.А. Энергосберегающие системы электропривода центробежных насосных агрегатов. Автореферат

Подождите немного. Документ загружается.

cцн

сн

СС

НС

ММ

−

),(

ωω η

, (3)

где Н

– статический напор, обусловленный разностью уровней начала

и конца трубопровода;

- напор насоса при закрытой задвижке (при подаче Q = 0).

На рисунке 3 представлены зависимости М

ст

=f(ω), М

ст

=f(Q),

рассчитанные по (3) для различных значений статического подпора.

На характер рассматриваемой зависимости существенным образом

влияет вид напорной характеристики сети, на которую работает ЦН, и

особенно соотношение между статической и динамической составляющими

требуемого напора. С увеличением Нс относительное значение момента

сопротивления Мс при той же частоте вращения становится меньше.

1 – Hc = 0 ; 2 – Hc = 0.2 ; 3 – Hc = 0.4.

Рисунок 3 - Механические характеристики ЦН.

Полученное выражение механической характеристики содержит

основные параметры напорных характеристик насоса, трубопровода,

изменение КПД при регулировании и позволяет в дальнейших исследованиях

точно учесть их, как нагрузку на валу привода.

Одной из наиболее эффективных возможностей энергосбережения

является создание объектно - ориентированных систем электропривода,

максимально учитывающих параметры и специфику работы приводного

механизма. На базе полученных зависимостей, характеризующих режимы

работы ЦН, проведен сопоставительный анализ возможных вариантов

регулируемого электропривода центробежных насосов: «преобразователь

частоты – асинхронный двигатель» (ПЧ – АД), «тиристорный регулятор

напряжения – асинхронный двигатель» (ТРН – АД), «вентильный двигатель»

(ВД), «асинхронный вентильный каскад» (АВК), «машина двойного

питания» (МДП). Недостатки систем ТРН – АД (недостаточный диапазон

регулирования), АВК (низкие энергетические показатели), ВД (сложность

реализации), а также накопленный положительный опыт эксплуатации

позволили выделить, как наиболее перспективные схемы АЭП ЦН, схемы

«преобразователь частоты – асинхронный двигатель» и «машина двойного

питания». Определены области возможного использования этих систем

электропривода.

К достоинствам широко распространенной системы ПЧ-АД следует

отнести следующее:

- высокий КПД в широком диапазоне регулирования скорости АД, так

как последний во всем диапазоне регулирования работает с малой величиной

скольжения ротора (малыми потерями скольжения);

- хорошие регулировочные свойства, обеспечивающие возможность

плавно регулировать скорость и формировать требуемые характеристики и

законы регулирования;

- надежность используемого в системе асинхронного двигателя с

короткозамкнутым ротором.

Он может быть рекомендован для насосных агрегатов, требующих

глубокого регулирования подачи и напора, частых пусков и остановов.

Применение этой системы для высоковольтных (6 – 10 кВ) двигателей

ограничено резким повышением стоимости ПЧ, связанной с применением

дополнительных трансформаторов, удорожанием элементной базы.

Электропривод центробежных механизмов – это область, в которой

частотному управлению имеется альтернатива – система с машиной

двойного питания. Достоинством МДП является пониженная мощность ПЧ в

цепи ротора. В них преобразуется не вся мощность, подводимая к насосному

агрегату, а только рекуперируемая мощность скольжения, которая в приводе

насосных агрегатов не превышает 18% номинальной мощности

электропривода; ограниченный диапазон регулирования насосов позволяет

использовать менее мощные и более простые преобразователи, чем при

частотном регулировании. Максимальное напряжение ПЧ в цепи ротора

высоковольтного АД не превышает 2 кВ, что снимает проблемы

высоковольтного преобразования мощности. Кроме того, МДП обладает

дополнительным резервом энергосбережения - возможностью регулирования

потребляемой реактивной мощности.

Обоснована область наиболее эффективного использования привода с

МДП - насосные агрегаты большой мощности с ограниченным диапазоном

регулирования скорости и редкими пусками.

Таким образом, к дальнейшим исследованиям приняты две системы

регулируемого электропривода центробежных агрегатов – ПЧ – АД и МДП.

Второй раздел работы посвящен исследованию и разработке

энергосберегающих систем и режимов работы систем электропривода

центробежных агрегатов по схемам «ПЧ – АД» и МДП.

В первом подразделе второго раздела определены методы расчета и

анализа, обобщающие исследование и описание различных систем

регулируемого асинхронного электропривода ЦН, получены

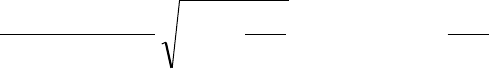
электромагнитные и электромеханические соотношения, характеризующие

их работу.

Полная система исходных уравнений, описывающих процессы в

асинхронном электроприводе центробежных насосов, состоит из четырех

групп: уравнений электромагнитного равновесия (Кирхгофа), описывающих

электромагнитные процессы в двигателе, уравнений электромеханического

преобразования энергии, уравнений, характеризующих особенности

механической нагрузки на валу двигателя и уравнений, отражающих

выходные параметры и свойства источников питания.

В качестве инструмента анализа электромагнитных процессов в приводе

определен векторно – гармонический метод, позволяющий исследовать

работу элементов привода во всех режимах работы центробежного агрегата.

Определен единый математический аппарат для описания и анализа двух

различных систем электропривода переменного тока - «ПЧ – АД» и МДП.

Получены основные соотношения для создания математических моделей

этих двух систем.

Взаимодействие полей статора и ротора ЭМП создает

электромагнитный момент в функции токов.

Для полного и адекватного описания процессов электромеханического

преобразования энергии в исследуемом электроприводе, известные

уравнения моментов АД решаются совместно с уточненным выражением

механической характеристики центробежных насосов, полученным в первом

разделе данной работы и учитывающем конструктивные и технологические

параметры ЦН и трубопровода.

Повысить качество расчетов позволяет и следующий шаг. К ротору АД

от двигателя приложен развиваемый им электромагнитный момент, а также

∆М

мех

– момент механических потерь АД. Момент механических потерь АД

линейно зависит от скорости и содержит составляющую трогания. Таким

образом, и момент сопротивления ЦН (3), и момент механических потерь АД

имеют составляющие трогания (при ω = 0) и составляющие, зависящие от

частоты вращения, которые, очевидно, следует объединить:

НС

МММ

мех

cцн

сн

мехСэм

ωω

ωω η

++−

+∆+=

)

),(

()(

. (4)

Полученное выражение (4), являясь новым уравнением движения

электропривода ЦН, вместе с известным уравнением АД описывает процессы

электромеханического преобразования энергии в динамическом и

установившемся режимах.

Второй подраздел второго раздела посвящен вопросам повышения

энергетической эффективности электропривода насосных агрегатов по схеме

«ПЧ – АД». Проведен анализ известных законов оптимального частотного

регулирования АД. Отмечено, что значительная часть проводимых в этом

направлении исследований посвящена улучшению регулировочных свойств

привода – точности, быстродействия и других динамических свойств. Однако

во многих случаях при синтезе таких САУ не уделяется достаточного

внимания энергетическим аспектам. В работах, посвященных минимизации

энергопотребления, не учитываются потери в стали машины, влияние

несинусоидальности питающего напряжения и распределения магнитной

индукции в машине, нелинейность характеристик намагничивания.

Первым этапом, позволяющим определить качественные

характеристики, закономерности и пути снижения потерь в частотно –

регулируемом электроприводе при работе на центробежную нагрузку, в

разделе стал аналитический метод, основанный на классическом

определении оптимального значения магнитного потока при известных

значениях относительных потерь в стали, обмотках АД в номинальном

режиме. Основным отличием от известных методов является применение в

расчетах уточненной механической характеристики ЦН, полученной нами

ранее:

)(

),(

)(

ωωη

ст

cцн

сн

опт

НС

−













, (5)

где k

, k

ст

, k

– относительные потери в обмотках, в стали и от тока

холостого хода.

Точность метода определяется точностью аппроксимации кривой

намагничивания.

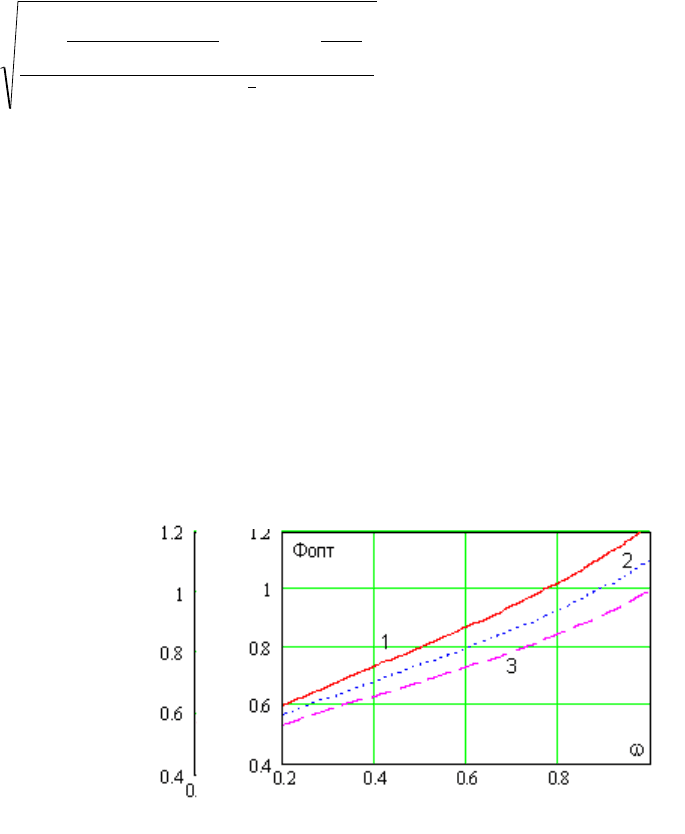
Рисунок 4,а иллюстрирует зависимость значений оптимального

магнитного потока от противодавления на выходе насосного агрегата.

«Обрыв» кривых 2 и 3 показывает снижение рабочего диапазона

регулирования скорости рабочего колеса насоса при увеличении величины

статического подпора трубопровода. Расчет проведен для тех же значений

весовых коэффициентов потерь.

а) б)

Рисунок 4 - Кривые Ф

опт

(ω) для

различных значений

статического подпора (а) и

относительных потерь в АД (б).

При выборе двигателей и

проектировании оптимальных

САУ для привода ЦН интерес

представляет влияние параметров

АД на характер изменения

оптимального магнитного потока в диапазоне регулирования скорости

рабочего колеса насоса. В частности, значение Ф

опт

в значительной степени

- k

=0.65, k

ст

=0.2; 2 - k

=0.55,

ст

=0.3; 3 - k

=0.45, k

ст

=0.4

1- Н

= 0; 2 - Н

= 0.3; 3 - Н

= 0.6

зависит от распределения потерь в АД в базовом режиме. На рисунке 4,б

приведены результаты расчетов оптимального значения магнитного потока

при значениях удельных потерь, наиболее распространенных в серийно

выпускаемых асинхронных двигателях

Следующим шагом исследования стал гармонический метод,

учитывающий несинусоидальность распределения магнитной индукции в

машине. При этом кривую намагничивания стали аппроксимируем в виде

гиперболического синуса, а магнитодвижущие силы представляем в виде

рядов с использованием функций Бесселя. Следует отметить, что метод

является хорошим инструментом для качественного анализа явлений,

поскольку позволяет выявить спектр гармонических, обусловленных

насыщением магнитопровода, основные соотношения и функциональные

связи, однако область его применения ограничивается, во-первых,

погрешностью, вносимой аппроксимацией кривой намагничивания в виде

гиперболического синуса, во-вторых, сложностью выражений,

получающихся при сложной геометрии магнитопровода.

Выполненные аналитические исследования позволили установить

основные закономерности для частотно-управляемого электропривода

центробежного насоса. Оценка точных количественных соотношений

выполнена на базе разработанного численного гармонического метода

расчета оптимального, по минимуму потерь, управления АД, учитывающей

нелинейность системы, конкретную геометрию сердечника машины и другие

факторы. Разработан алгоритм решения задачи.

Все процессы в АД описываются системой нелинейных уравнений МДС

F, ЭДС, E и моментов M, которые являются неявными функциями амплитуд

гармонических магнитной индукции по продольной и поперечной осям.

Величина последних по участкам магнитной цепи зависит от значения

амплитуд магнитной индукции в воздушном зазоре В

δi

, которые и являются

корнями системы нелинейных уравнений.

На базе гармонического метода разработана математическая модель

системы «частотно-управляемый асинхронный двигатель – центробежный

насос» с учетом технологических параметров ЦН, геометрических

параметров сердечника машины, реальной картины распределения

магнитной индукции. Модель учитывает всю совокупность электрических

параметров, конструкционных параметров сердечника и, главное, весьма

точно учитывает нелинейность магнитной цепи.

На полученной модели выполнены численные исследования, в

результате которых выявлены основные закономерности и пути снижения

потерь в двигателе. Рассчитаны законы оптимального, по минимуму потерь

в двигателе, частотного управления приводом ЦН для различных вариантов

исполнения сердечника АД. Полученные при этом рабочие характеристики

АД подтверждают работоспособность предложенных алгоритмов управления

и высокий уровень энергетических показателей.

Разработанная математическая модель может быть непосредственно

использована, как элемент системы автоматического управления

P1(1-s)

ПЧ

P1s

электроприводом по схеме «ПЧ – АД» центробежных агрегатов,

оптимизированной по энергопотреблению.

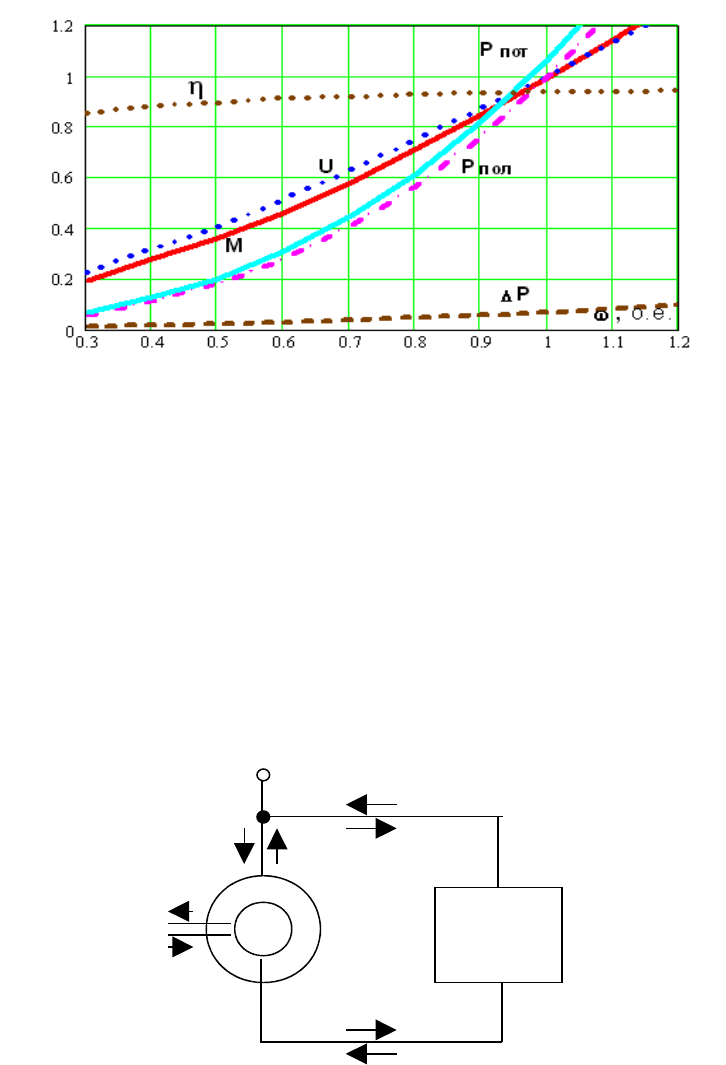
На рисунке 5 представлены рабочие характеристики АД – момент,

полезная и потребляемая мощность, мощность потерь. При использовании

предложенного оптимального, по минимуму потерь, закона частотного

управления значение КПД во всем диапазоне регулирования подачи ЦН

остается высоким и равным номинальному.

Рисунок

5 – Рабочие характеристики АД в диапазоне регулирования ЦН при

оптимальном частотном регулировании.

В третьем подразделе второго раздела рассматривается

энергосберегающий электропривод ЦН по схеме машины двойного питания,

рисунок 6.

Энергопотребление МДП и расчет энергетических показателей, по

сравнению с другими схемами управления АД, имеет ряд особенностей.

В МДП частота вращения ротора асинхронного двигателя изменяется

благодаря введению в цепь ротора добавочного напряжения U

. Это

напряжение может управляться по модулю, частоте и фазе.

Рисунок 6 – Машина двойного питания.

В общем случае вектор U

отстает от вектора напряжения статора на

угол δ. Если совместить ось x вращающихся координат с U

, условие

электромагнитного равновесия в установившемся режиме обеспечивается

при

mmx

rllssl

llsrsl

lrll

lllr

2211

2121

1111

)(0

0)(

sin

cos

+−−

−+−

ωω

, (6)

где i

– токи статора и ротора АД;

–индуктивности рассеяния фазы статора и ротора;

– индуктивность контура намагничивания;

, rr

– активные сопротивления фазы статора и ротора;

– угловая частота вращения поля статора;

s =(ω

– ω)/ ω

– скольжение.

Векторы токов статора и ротора в установившемся режиме

определяются, как

3421

2312

ZZZZ

UZUZ

−

;

3421

2114

ZZZZ

UZUZ

−

+−

; (7)

где

110

101

)(

rll

llr

+−

- субматрица сопротивлений статора;

220

202

)(

rlls

llsr

+−

- субматрица сопротивлений ротора;

−

- субматрица сопротивлений намагничивающей

цепи;

−

- субматрица сопротивлений намагничивающей

цепи.

Электромеханическое преобразование энергии в МДП описывается в

соответствии с (4).

Расчет статических режимов работы МДП сводится к определению

значений U

и δ из совместного решения уравнений электрического

равновесия (6) и электромеханического равновесия с учетом (4). Разработана

программа, которая используется для расчета U

, δ, первых гармоник

напряжений и токов и их фазовые сдвиги, необходимые для обеспечения

того или иного режима работы МДП. Таким образом, нами получена

математическая модель электропривода центробежного насоса по схеме

машины двойного питания.

Ядром модели является программный блок «Matrix», в котором

производится расчет системы нелинейных алгебраических (в

установившемся режиме) или дифференциальных (в переходных режимах)

уравнений численными методами. Для конкретного двигателя и заданных

технологических и энергетических параметров рассчитываются необходимое

выходное напряжение ПЧ, токи и напряжения двигателя.

В разделе выполнены аналитические исследования с целью

определения энергосберегающих возможностей электропривода

центробежных насосов по схеме машины двойного питания. Показано, что,

при центробежной нагрузке по сравнению с частотно – управляемым

асинхронным приводом, машина двойного питания имеет еще один, очень

важный резерв – регулирование реактивной мощности.

Проведен анализ известных законов оптимального управления МДП и

предложен новый вариант регулирования реактивной мощности – по

номинальному току ротора. Согласно последнему, в значительном диапазоне

регулирования ЦН, АД работает с опережающим коэффициентом мощности,

то есть в режиме компенсатора реактивной мощности. Составлен алгоритм

управления и программы расчета энергетических характеристик для нового

способа оптимального управления.

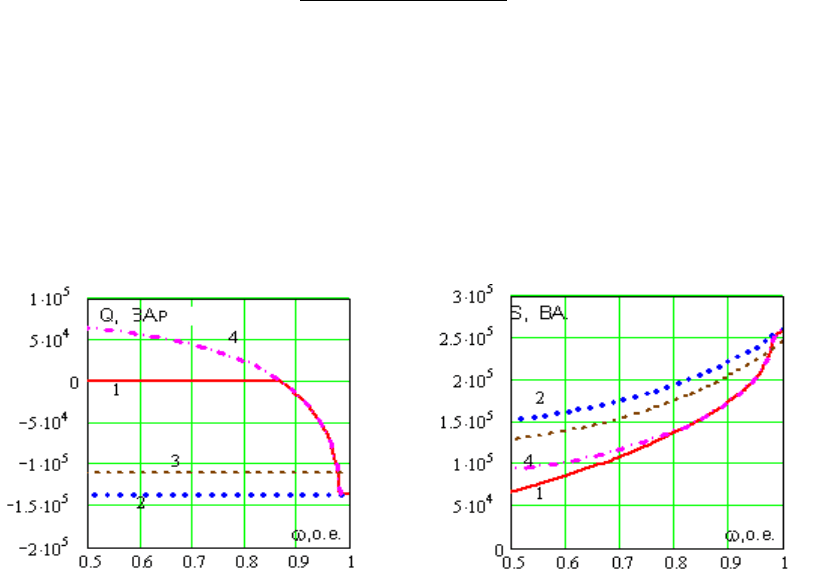
На рисунке 7 приведены значения реактивной и полной мощности, а

также коэффициента сдвига статорной цепи

АДC

двигателя 4АНК 315 4У3

мощностью 200кВт, рассчитанные для различных законов регулирования

приводом ЦН. При регулировании по Q1=0 значение

АДC

в значительном

диапазоне регулирования (пока двигатель недогружен) остается равным 1.

При реализации регулирования по номинальному току ротора, АД в этих же

пределах регулирования насоса работает компенсатором реактивной

мощности (кривая 4 на рисунке 7).

Проведенные расчеты показывают, что повышение k

двигателя МДП

при применении специальных законов управления сопровождается

некоторым снижением КПД. Для комплексной оценки энергетической

эффективности предлагается сопоставление по приведенному значению КПД

( )

пр

tgtg

ϕϕκ

−+

∋

, (8)

где

∋

- удельные потери, связанные с генерированием 1 кВАр

реактивной мощности, кВт/кВАр;

- номинальный показатель данного электродвигателя.

a )

с)

1 – Q1=0; 2 – Q2=0; 3 – ΔP – min;

4 – I2 =I2н(опережающий).

Рисунок 7 – Реактивная (а), полная (b) мощности и коэффициент сдвига (с)

статорной цепи АД.

Результаты расчета приведенного значения КПД, проведенного по

формуле (8) для различных законов управления МДП – привода ЦН (рисунок

8), показали значительное преимущество регулирования по номинальному

значению тока ротора.

Расчет

суммарных энергетических параметров привода по схеме машины двойного

питания имеет свои особенности. В разделе разработана математическая

модель для исследования энергетических показателей электропривода

центробежных насосов с машиной двойного питания.

На рисунке 9 представлена схема МДП и указаны величины,

характеризующие ее энергетику.

МДП

ИМДП

МДП

1 – Q1=0; 2 – Q2=0; 3 – ΔP – min; 4 – I2 =I2н

Рисунок 8 – Приведенный КПД двигателя в схеме МДП.

Рисунок 9 – Составляющие мощности и энергетические показатели

МДП

Мощности и коэффициенты искажения определяются в разделе 4

данной работы. Для расчета энергетики привода ЦН с МДП разработана

программа, блок – схема алгоритма которой представлена на рисунке 10.

Составляющие мощности АД в режиме МДП определяются, кроме

частоты вращения и момента на валу, законом регулирования реактивной

мощности. Активная мощность статора Р

1АД

зависит от нагрузки двигателя и

частоты вращения, реактивная Q

1АД

– от закона регулирования (функций

регулирования), принятых в данном конкретном случае.

Мощность на входе НПЧ Р

1НПЧ

, за вычетом потерь, соответствует

активной мощности скольжения АД Р

, а реактивная Q

1НПЧ

является

функцией коэффициента мощности роторной цепи, величины и частоты

напряжения, подаваемого в ротор.

Таким образом, расчет энергетики МДП по первым гармоническим

токов и напряжений должен проводиться в следующей последовательности.

1. В подпрограмме “Matrix” по заданным параметрам АД,

трубопровода, насоса, варианта оптимизации (различных законов

регулирования реактивной мощности МДП) определяются необходимые

значения U

и δ (функции регулирования - величина и фаза подводимого к

ротору АД напряжения), обеспечивающие выбранный режим работы

центробежного насоса и привода во всем диапазоне регулирования. Для этого

небходимо решить совместно уравнения электрического равновесия АД в

режиме двойного питания и момента на валу двигателя. В нашем случае

момент сопротивления является достаточно сложной функцией частоты

вращения ротора АД.

AД

НПЧ

2222

SPQP

222 MADИADC

KKK

СМДП

ИМДП

ММДП

С1НПЧ

И1НПЧ

М1НПЧ

1НПЧ

И1НПЧ

1НПЧ

1AД

ИAД

1AД

C1AD

И1AD

M1AD

Параметры АД

параметры: Qн,H Энергетические

параметры