Mourachkine A. Room-Temperature Superconductivity

Подождите немного. Документ загружается.

224 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3.10 Energy gaps ∆

and ∆

The energy gap is one of the most important characteristics of the supercon-

ducting state. Since the discovery of high-T

superconductivity in the cuprates,

they have been extensively studied by different experimental techniques. Sur-

prisingly in the cuprates, different techniques have initially provided different

values of an energy gap. The discrepancy remained a mystery until it was

realized that different experimental methods probe two different energy gaps.

Moreover, the magnitudes of the two gaps strongly depend on the doping level.

The energy gap ∆

is the bisoliton pairing gap shown in Fig. 6.23, and

2∆

measures the strength of the binding of two quasiparticles. The phase-

coherence energy gap 2∆

is the condensation energy of a Cooper pair when

the long-range phase coherence appears. Hence, quasiparticles in the cuprates

undergo two condensations: the ﬁrst when they become paired, and the second

when the long-range phase coherence sets in. The total energy gain per quasi-

particle is not (∆

+∆

) but ∆



∆

+∆

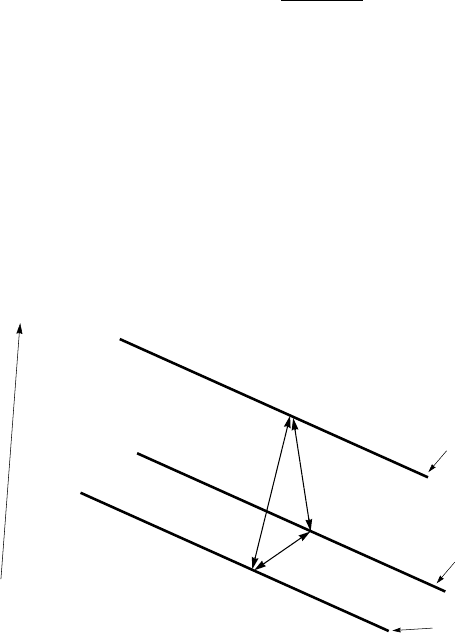
. Figure 6.40 schematically

shows these three energy gaps relative to the Fermi level (F) in three dimen-

sions. The bisoliton energy level (B) is below the Fermi level by ∆

, and it is

separated by ∆

from the energy level of the superconducting condensate (SC).

In Fig. 6.40, each Cooper pair at the SC level has two possibilities: either to

be excited or to be broken. The ﬁrst possibility corresponds to the transition

SC → B in Fig. 6.40, that requires a minimum energy of 2∆

. The sec-

ond choice is the transition SC → F in Fig. 6.40 which requires a minimum

energyof2∆

. The bisolitons at the B energy level in Fig. 6.40 are uncon-

densed Cooper pairs; therefore, they are not in phase with the superconducting

condensate. To break up a bisoliton which is at the B energy level, a minimum

Fermi level

bisolitons

condensate

∆

Figure 6.40. Three energy levels of quasiparticles in unconventional superconductors in three

dimensions (for more details, see text).

Third group of superconductors: Mechanism of superconductivity 225

0 0.05 0.1 0.15 0.2 0.25 0.3

Doping level, p

2∆/

k T

c,max

∆

Figure 6.41. Low-temperature phase diagram of superconducting cuprates: the pairing energy

scale ∆

and the Cooper-pair condensation scales ∆

energyof2∆

must be supplied.

Figure 6.41 shows three energy scales ∆

, ∆

and



∆

+∆

in Bi2212

as a function of doping level. ∆

and ∆

are given by Eqs. (6.9) and (6.7),

respectively. Such a phase diagram is typical for hole-doped cuprates. From

Fig. 6.41, one can see that the two energy scales ∆

and



∆

+∆

have

similar magnitudes. In the cuprates, depending on the type of an experiment

(bulk or surface-layer sensitive; sensitive to single-quasiparticle excitations or

to the coherence properties of the condensate), measurements may show one,

two or three energy scales which are depicted in Fig. 6.41. It is worth noting

that the pairing gap ∆

is an in-plane energy scale, while the phase-coherence

gap ∆

is mainly a c-axis energy scale.

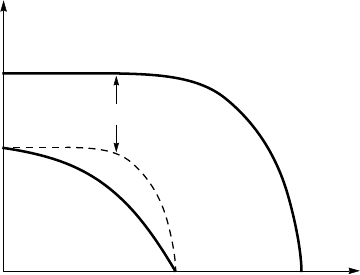
The temperature dependences of the two energy gaps, ∆

and ∆

, are pre-

sented in Fig. 6.42. The ∆

(T ) dependence is similar to the BCS temperature

dependence, while the ∆

(T ) dependence lies below the BCS temperature de-

pendence, and is similar to the temperature dependences of (in)commensurate

peak(s) depicted in Fig. 6.36.

In conventional superconductors, the order parameter Ψ is proportional to

the Cooper-pair wavefunction ψ, and has an s-wave symmetry (angular mo-

mentum  = 0). In the cuprates, the order parameter and the Cooper-pair wave-

function are different, and have different symmetries. Therefore, the symme-

tries of the energy gaps ∆

and ∆

are also different. In the cuprates, all phase-

sensitive measurements show that the order parameter in hole- and electron-

doped cuprates has the d

−y

(d-wave) symmetry, shown in Fig. 6.43. Then,

the energy gap ∆

has also the d-wave symmetry. A key feature distinguishing

the d

−y

symmetry is that it has two positive and two negative lobes and four

226 ROOM-TEMPERATURE SUPERCONDUCTIVITY

pair

∆

(

)

∆

(0)

∆

(0)

∆

(

)

∆

(

)

BCS

Figure 6.42. Temperature dependences of ∆

and ∆

, shown schematically. The ∆

(T ) de-

pendence lies below the BCS temperature dependence.

nodes between the lobes, as sketched in Fig. 6.43. As discussed above, spin

ﬂuctuations mediate superconductivity exclusively with a d

−y

ground state.

What is the symmetry of the pairing (bisoliton) wavefunction? The pairing

wavefunction must have an s-wave symmetry. Many experiments mainly tun-

neling clearly show the presence of an s-wave component in the cuprates. To

explain these experimental data, one must assume that the Cooper-pair wave-

functions have an s-wave symmetry. Fortunately, we know that phonons are

mainly responsible for the pairing in the cuprates, and they indeed favor an

electron pairing with an s-wave symmetry.

ARPES and tunneling measurements performed in Bi2212 show that the

gap ∆

is anisotropic and has a four-fold symmetry. In addition to a usual

anisotropic s-wave symmetry, ∆

can also have an extended s-wave symmetry

schematically shown in Fig. 6.44. In the latter case, the gap is everywhere

positive (negative) except four small lobes where the gap is negative (positive).

In Fig. 6.44, the case of s-wave gap with nodes is an intermediate case between

the two cases—anisotropic and extended.

In heavy fermions, the situation is very similar. For example, in UBe

Andreev-reﬂection measurements show the presence of a d-wave gap, while

tunneling measurements show that UBe

is an s-wave superconductor (see

references in [19]).

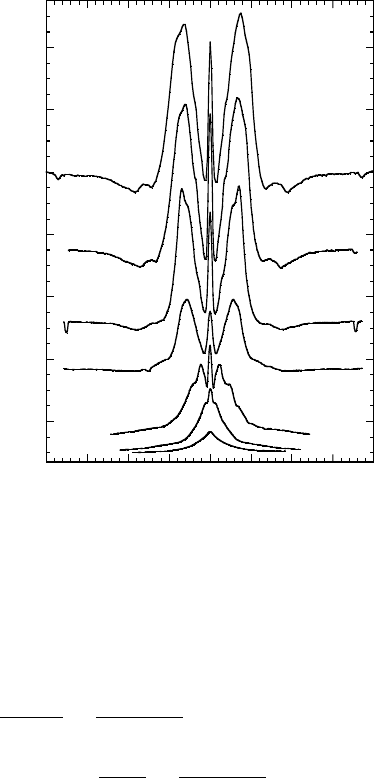
At the end of this subsection, let us consider a set of tunneling data to visu-

alize the two gaps ∆

and ∆

. In these tunneling data, the two gaps manifest

themselves simultaneously. Figure 6.45 shows a temperature dependence of a

conductance obtained in Ni-doped Bi2212 having T

 75K(p ∼ 0.2). In the

plot, one can see that the conductance peaks are composite, especially, those

Third group of superconductors: Mechanism of superconductivity 227

Figure 6.43. Superconducting order parameter in hole-doped cuprates, shown in real space: it

has the d

−y

shape.

at 41.8 K. As was discussed in [19], these data were measured by chance near

an impurity, i.e. a Ni atom. Since Ni is a magnetic impurity in the CuO

planes, it is able to participate in the Cu-spin ﬂuctuations. At the same time,

Ni breaks up the Cooper pairs in the CuO

planes. In terms of the two gaps,

this means that, in its vicinity, Ni destroys ∆

, whilst ∆

remains practically

unchanged. In Fig. 6.45, both gaps have practically the same magnitudes at

15 K, ∆

 ∆

 17.5 meV (this can easily be seen in the corresponding

I(V ) characteristics which are not shown here; for more details, see Chapter 6

in [19]). It is important to emphasize that such a situation is only possible lo-

cally. In Fig. 6.45, one can see that the quasiparticle peaks disappear between

65.3 K and 70.3 K. This means that, locally, ∆

closes in this temperature in-

terval. Taking the mean value T

∆

=(65.3+70.3)/2  67.8 K, we have

∆

 0.91. This enables us to determine the gap ratios for the two gaps

anisotropic

extended

with nodes

Figure 6.44. Possible types of s-wave symmetry of the pairing wavefunction in the cuprates,

shown in real space: (a) anisotropic, (b) extended and (c) with nodes. The case (c) is intermedi-

ate between (a) and (b).

228 ROOM-TEMPERATURE SUPERCONDUCTIVITY

-200 -100 0 100 200

25.6 K

15 K

41.8 K

51.3 K

59.3 K

65.3 K

70.3 K

Bias (mV)

dI/dV (norm.)

Figure 6.45. Temperature dependence of SIS-junction tunneling conductance obtained in a

Ni-doped Bi2212 single crystal with T

= 75 K [19]. The conductance scale corresponds to the

70.3 K spectrum, the other spectra are offset vertically for clarity. The peak at zero bias is due

to the Josephson current in the junction.

in Bi2212:

2∆

∆



35 meV

5.83 meV

 6(±0.2) and (6.68)

2∆



35 meV

6.45 meV

 5.43. (6.69)

This example is also instructive because it helps to visualize gapless super-

conductivity in unconventional superconductors. In this example, the Cooper

pairs do not exist between T/T

= 0.91 and 1 near the Ni atom, while the

Ni spin participates in local spin ﬂuctuations. In Fig. 6.45, one can see that

the 70.3 K conductance does not have quasiparticle peaks, but it exhibits a

small zero-bias peak due to the Josephson current. This means that, in the Ni

vicinity, between T/T

= 0.91 and 1, the phase coherence is sustained. In

this case, superconductivity is locally gapless. Thus, in the interval T/T

0.91 and 1, all Cooper pairs (bisolitons) passing by the Ni atom are broken,

while the ﬂuctuations of Cu spins are not interrupted by the Ni atom. Thus,

Third group of superconductors: Mechanism of superconductivity 229

gapless superconductivity can arise in unconventional superconductors but ex-

clusively locally. This is in contrast to conventional superconductors where

gapless superconductivity can exist in a whole sample (see Chapter 2). From

this example in Fig. 6.45, one can also have a feeling for the magnetic origin

of the phase coherence mechanism in Bi2212.

3.11 Quantum critical point and the condensation energy

In cuprates, the doping level p = 0.19 is a quantum critical point where mag-

netic ﬂuctuations are the strongest. Since spin ﬂuctuations mediate the phase

coherence in the cuprates, superconductivity at low temperature is the most

robust at this doping level, p = 0.19, and not at p = 0.16. The superconducting

condensation energy as a function of doping has a maximum at p = 0.19, as

shown in Fig. 6.46. The maximum values of U

for YBCO and Bi2212 are

0,max

= 2.6 J/g atoms and U

0,max

= 2 J/g atoms, respectively. From Fig.

6.46, superconductivity in the underdoped region is very weak. At p = 0.19,

the superconducting-phase fraction is a maximum as well, as sketched in Fig.

6.8b. The temperature/energy scale T

in Fig. 6.11 starts/ends in the quan-

tum critical point. Hence, it has the magnetic origin.

0.16

0.05

0.27

0.1

0.19

0,max

YBCO

Bi2212

Figure 6.46. Superconducting condensation energy U

as a function of doping level, obtained

in Bi2212 and YBCO by heat-capacity measurements (see references in [19]).

3.12 Effective mass anisotropy

Because of a layered structure of the cuprates, quasiparticles move much

more easily in the CuO

planes than between the planes. Thus, anisotropy of

the crystal structure of the cuprates affects transport properties. To account

for the anisotropy, it is conventionally agreed that the effective mass changes

with crystal direction. Instead of being a single-valued scalar m, the effective

electron mass becomes a tensor. In the cuprates, to a good approximation, the

effective electron mass is a diagonal tensor, and the in-plane effective masses

230 ROOM-TEMPERATURE SUPERCONDUCTIVITY

have similar values, m

≈ m

. The value of the in-plane effective mass in

the cuprates is slightly larger than the electron mass m

by a factor of between

four and ﬁve: m

 (4–5)m

Anisotropy is deﬁned by the ratio of the effective mass of quasiparticles in

the various directions, γ

. In YBCO, the effective mass ratio is about

≈ 30. LSCO exhibits somewhat higher anisotropy, γ

≈ 200, while Bi-

and Tl-based cuprates are much more anisotropic than YBCO: in Bi- and Tl-

compounds, the ratio is about 50000. Such a large anisotropy, which is totally

foreign to conventional superconductors, means that electrons can barely move

in the c-axis direction, and the cuprates are effectively two-dimensional.

3.13 Penetration depth

The penetration depth λ is one of the most important parameters of the

superconducting state because λ directly relates to the superﬂuid density as

∝ 1/λ

. Table 3.6 lists the penetration-depth data for some cuprates. In

the table, one can see that, in the cuprates, λ is very large, particularly, in the

c-axis direction, meaning that n

is very low.

In the Uemura plot in Fig. 3.6, the T

value depends linearly on the super-

ﬂuid density in underdoped cuprates, and this dependence is universal for all

superconducting cuprates. As the doping level increases, T

ﬁrst saturates and,

in the overdoped region, decreases, making a “boomerang path”, as shown in

the lower inset of Fig. 3.6. Thus, in the overdoped region, the superﬂuid den-

sity falls with increased doping. The Uemura plot shows that the optimum

doping level is different for different cuprates.

Figure 6.47 shows the doping dependence of the penetration depth in LSCO;

thus, a sort of “inverted” Uemura plot. One notes from Figs 3.6 and 6.47,

the penetration depth as a function of doping attains a minimum not in the

optimally doped region but in the slightly overdoped region. In Bi2212, the

in-plane penetration depth has the same trend.

It is worth noting that, in YBCO, due to the presence of chains, the penetra-

tion depth is smaller along the chains than that along the a axis: in YBCO with

=93K,λ

= 1550–1600 A

◦

and λ

= 800–1000 A

◦

. The value λ

= 1450 A

◦

listed in Table 3.6 for YBCO, represents the value of

√

3.14 Critical ﬁelds and current

All superconducting cuprates are type-II superconductors. Hence, they have

two critical magnetic ﬁelds: H

(0) and H

(0). In Table 3.6, one observes

that the magnitudes of the second critical magnetic ﬁeld, H

(0), are extremely

high in the cuprates. At the moment of writing, the cuprates exhibit the largest

values of H

(0) amongst all unconventional superconductors.

Third group of superconductors: Mechanism of superconductivity 231

0.16

0.05

0.27

0.28

0.1

0.19

(µ

0.2

(µ

LSCO

Figure 6.47. Absolute values of the in-plane λ

and out-of-plane λ

magnetic penetration

depth as a function of doping for LSCO (see references in [19]). The dashed line showstendency

of λ

at high doping, expected from Fig. 3.6.

Furthermore, due to a highly anisotropic structure of the cuprates, there is a

huge anisotropy of the critical magnetic ﬁelds applied parallel and perpendic-

ular to the CuO

planes. Thus, in the cuprates, there are four different critical

magnetic ﬁelds: H

c1,

(0), H

c1,⊥

(0), H

c2,

(0) and H

c2,⊥

(0). The symbols 

and ⊥ denote the critical value of H applied parallel and perpendicular to the

CuO

planes, respectively. In the cuprates, H

is much larger when the ﬁeld

is applied parallel to the CuO

planes than that applied perpendicular to the

planes. This is because most of the conduction is in the planes: a magnetic

ﬁeld applied parallel to the planes is not very effective in destroying supercon-

ductivity within the planes.

In the cuprates, the lower critical ﬁelds H

c1,

and H

c1,⊥

are very small. For

example, in YBCO H

c1,

∼ 2 ×10

−2

T and H

c1,⊥

∼ 5 ×10

−2

T; in Hg1223,

c1,

≈ 3 × 10

−2

T. It is interesting that the anisotropy in H

has the sign

opposite to that in H

: H

c2,⊥

c2,

but H

c1,⊥

c1,

It is worth noting that the majority of H

values in Table 3.6 are approxi-

mate because they are extrapolated from the resistivity data obtained near T

The magnetic ﬁelds accessible in the laboratory conditions are only of the order

of 30 T. Secondly, in metallic superconductors described by the BCS theory,

∝ T

. In the cuprates, the relation is found to be different: H

∝ T

√

determined in the cuprates with low T

The critical current in layered cuprates is also very anisotropic. The highest

values of the critical current J

were obtained in epitaxial thin ﬁlms of YBCO.

At liquid helium temperature, the critical current in the ab plane is almost 10

A/cm

and, along the c axis, is of the order of 10

A/cm

232 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3.15 Coherence length and the size of a Cooper pair

As deﬁned in Chapter 2, the coherence length ξ

is determined by varia-

tions of the order parameter Ψ(r), whilst the Cooper-pair size ξ is related to

the wavefunction of a Cooper pair, ψ(r). While the coherence length depends

on temperature, ξ

(T ), the Cooper-pair size is temperature-independent. In

contrast to conventional superconductors, the order parameter and the Cooper-

pair wavefunction in all unconventional superconductors are independent of

one another. Therefore, generally speaking, in unconventional superconduc-

tors, ξ

= ξ at any temperature.

Let us consider ﬁrst the in-plane ξ

GL,ab

and ξ

. Since the Cooper pairs in

the cuprates reside into the CuO

planes, the size of a Cooper pair is, by def-

inition, an in-plane characteristic and thus ξ ≡ ξ

. The magnetic ﬁeld H

c2,⊥

directly relates to the in-plane coherence length ξ

GL,ab

through Eq. (2.67).

As was analyzed in [19], for the cuprates, the ﬁeld H

c2,⊥

, in fact, yields the

value of ξ or, at least, a value which is very close to ξ. How is it possible?

This fact may indeed look odd because, by applying a magnetic ﬁeld to a sys-

tem which is characterized by two coupling strengths, it is anticipated that

the weaker “bond” will ﬁrst be suppressed. In the cuprates, depending on the

doping level, the strength of the electron-phonon interaction (∼ 0.6 eV) can

be four times stronger than the strength of magnetic interaction (J ∼ 0.15

eV). Experimentally, however, for cuprates the magnetic ﬁeld H

c2,⊥

yields the

value of ξ which is mainly determined by the electron-phonon interaction. As

discussed above, the mechanism of in-plane phase coherence in the cuprates

is not purely magnetic: the direct wavefunction hopping largely contributes

to the onset of in-plane phase coherence. Therefore, even if the in-plane spin

ﬂuctuations are suppressed, there will always be superconducting patches due

to the direct wavefunction hopping. It is then obvious why, in the cuprates, the

ﬁeld H

c2,⊥

yields the value of ξ and not ξ

GL,ab

. The doping dependence of ξ

in Bi2212 is shown in Fig. 6.25.

To obtain ξ

GL,ab

in the cuprates, another method has been proposed. In

LSCO, ξ

GL,ab

was determined by measuring the vortex-core size [50]. Fig-

ure 6.48 depicts the doping dependences of ξ

GL,ab

and ξ in LSCO, obtained

at low temperature. The dependence ξ(p) was obtained through H

as de-

scribed in the previous paragraph. In Fig. 6.48, one can see that the depen-

dence ξ

GL,ab

(p) has an inverted bell-like shape similar to the dependence λ(p)

in Fig. 6.47. Both these dependences directly follow from the fact that the

dependence ∆

(p) has a bell-like shape (see Fig. 10.14 in [19]). At p  1/8,

GL,ab

(p) has a kink related to the

anomaly (see Chapter 3). At p  0.05,

the value of ξ

GL,ab

in LSCO is about 70 A

◦

. In Fig. 6.48, one can see that, in

the overdoped region, ξ

GL,ab

 ξ.

Third group of superconductors: Mechanism of superconductivity 233

(

)

(

)

0.05

0.27

1/8

In-plane

and

LSCO

Figure 6.48. Sketch of doping dependences of in-plane ξ

and ξ in LSCO, obtained at low

temperature [50].

In the cuprates, the in-plane magnetic correlation length is sufﬁciently large.

For example, in LSCO, the value of in-plane magnetic correlation length is

> 400 A

◦

[51]. If we substitute this value into Eq. (2.67), we obtain

that H

c,m

< 0.2 T. This value is of the same order of magnitude as H

c1,⊥

∼

0.05 T in YBCO (see above). So, it is possible that, in the cuprates, the in-plane

magnetic correlation length determines H

c1,⊥

. However, one must realize that

has no relations with ξ

GL,ab

The in-plane coherence length ξ

GL,ab

is determined by a length of dynamic

magnetic characteristics, and not static ones as ξ

. In the cuprates, ξ

GL,ab

re-

lates most likely to the coherence length of incommensurate spin ﬂuctuations

which are in fact commensurate locally but manifest themselves in INS spectra

as incommensurate. For example, in underdoped YBCO, the minimum coher-

ence length of the magnetic resonance peak is practically doping-independent

and is about 16 A

◦

. At the same time, the minimum coherence length of the

incommensurate spin ﬂuctuations decreases from 35 to 24 A

◦

as the doping

level increases [52]. Thus, in underdoped YBCO, the doping dependence of

minimum coherence length of incommensurate spin ﬂuctuations is similar to

the dependence ξ

GL,ab

(p) for LSCO, shown in Fig. 6.48, whilst the minimum

coherence length of the magnetic resonance peak is doping-independent [52].

Consider now the out-of-plane ξ

GL,c

and ξ

. The dependence ξ

GL,c

(p) must

correlate with ξ

GL,ab

(p) shown in Fig. 6.48. In contrast, ξ

should increase

as the doping level increases (see Fig. 10.15b in [19]) because, as the doping

level increases, the cuprates become more three-dimensional. For cuprates,

the values listed in Table 3.6 are the values obtained by using Eq. (2.68) and,

formally, correspond to ξ

GL,c

. However, it seems that these values are the

values. Does this mean that, in the cuprates, the direct interlayer hopping