Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

191

Критерии управляемости. для того чтобы система была

управляемой, необходимо и достаточно выполнение одного из

следующих условий:

– матрица управляемости имеет полный ранг:

rank ,n=R

– грамиан управляемости невырожден:

0det .

¹W

Критерии наблюдаемости. для того чтобы система была на-

блюдаемой, необходимо и достаточно выполнение одного из сле-

дующих условий:

– матрица наблюдаемости имеет полный ранг:

rank ,n=D

– грамиан наблюдаемости невырожден:

0det .

¹W

6.6. Анализ минимальности линейных моделей

одной и той же передаточной функции Q(p) соответствует це-

лый класс эквивалентных реализаций в пространстве состояний

{ф-ла (6.4)}, характеризуемых различными тройками матриц (A,

b, c) разных, вообще говоря, размеров. реализация называет-

ся минимальной, если размер ее матрицы A наименьший среди

всех эквивалентных реализаций. Поиск такой реализации имеет

практический смысл, так как ее моделирование на эвМ требует

меньших вычислительных затрат.

для анализа минимальности конкретной реализации нужно

проверить ее управляемость и наблюдаемость. для того чтобы реа-

лизация {ф-лы (6.4)} была минимальной, необходимо и достаточно,

чтобы она была управляемой и наблюдаемой одновременно. этот

результат – минимальность любой управляемой и наблюдаемой

реализации – играет важную роль в теории линейных систем.

Поскольку невырожденность кросс-грамиана является крите-

рием одновременной управляемости и наблюдаемости системы,

то это может служить одним из условий минимальности реали-

зации скалярной системы.

Критерии минимальности. для того чтобы реализация си-

стемы была минимальной, необходимо и достаточно выполнение

одного из следующих условий:

– обе матрицы R и D имеют полный ранг:

rank ,n=R

;rank n=D

– матрица DR имеет полный ранг:

rank(),n=DR

– оба грамиана W

и W

невырождены:

0det ,

¹W

0;det

¹W

– матрица W

невырождена:

0;det( )

¹WW

– кросс-грамиан невырожден:

0det .

¹W

192

таким образом, минимальность системы определяется свой-

ствами тройки матриц А, b, с. напомним, что устойчивость си-

стемы определялась свойствами только одной матрицы А, управ-

ляемость – свойствами пары матриц А, b, а наблюдаемость –

свойствами пары матриц А, с.

на практике проще всего использовать первое из пяти пере-

численных условий. в соответствии с ним анализ минималь-

ности конкретной реализации сводится к проверке пары кри-

териев

rank ,n=R

rank .n=D

если хотя бы один из рангов

меньше n, то реализация неминимальна. размерность эквива-

лентной минимальной реализации n

определяется по формуле

( )

rank .n = DR

если в результате анализа оказалось, что система немини-

мальна, то ее порядок можно понизить. это можно сделать,

перейдя от описания в пространстве состояний к передаточной

функции

()

() ( ) .

()

Qp p

=- =cE b

(6.10)

затем нужно выделить общий множитель в полиномах А(р),

В(р) и сократить на него. эта процедура известна как сокраще-

ние совпадающих нулей и полюсов системы. Предварительно

следует выполнить разложение передаточной функции на про-

стейшие сомножители (так называемое нуль-полюсное или zpk-

представление):

( )( )

() ,

( )( )

p z ... p z

Qp k

p p ... p p

и выявить одинаковые сомножители в числителе и знаменателе.

При этом уменьшение размерности системы будет равно числу

пар совпадающих (или незначительно отличающихся) нулей и

полюсов.

в пакете MATLAB для вычисления нулей и полюсов можно

использовать функции zero, pole, pzmap, zpk. Аргументом во

всех случаях служит исследуемая система sys, предварительно

сформированная командами ss или tf.

другой подход к построению минимальной реализации осно-

ван на выделении неуправляемой и ненаблюдаемой подсистем

исходной системы и их удалении. При этом может использова-

ться преобразование линейной системы к одной из канонических

форм. в частности, в библиотеке CONTROL пакета MATLAB име-

193

ются команды ctrbf (controllability form) и obsvf (observability

form), обеспечивающие переход к управляемой и наблюдаемой

сопровождающим каноническим формам.

эти канонические формы положены в основу операции

minreal (сокращение от minimal realization), осуществляющей

удаление неуправляемой и ненаблюдаемой подсистем, что эк-

вивалентно сокращению одинаковых полюсов и нулей системы.

результатом операции является описание модели пониженной

размерности, причем полученная модель будет управляемой, на-

блюдаемой и минимальной.

Каноническая декомпозиция Калмана. исчерпывающий от-

вет на вопрос о структуре системы и порядке ее минимальной

реализации дает каноническая декомпозиция калмана. в соот-

ветствии с ней любую систему можно разбить на четыре подси-

стемы: управляемую и наблюдаемую (6.4), неуправляемую на-

блюдаемую (6.5), управляемую ненаблюдаемую (6.6), неуправ-

ляемую и ненаблюдаемую (6.8).

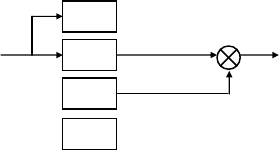
это иллюстрируется рис. 6.21, на котором показаны суще-

ственные связи между подсистемами (возможны также некото-

рые дополнительные связи, например с подсистемы 1 на подси-

стему 3 или с подсистемы 2 на подсистему 4).

Z













Рис. 6.21. Декомпозиция Калмана

Подсистемы 2, 3, 4 не вносят вклада в передаточную функцию

системы и могут не учитываться при моделировании. Подсисте-

ма 1 представляет собой минимальную реализацию. она явля-

ется управляемой и наблюдаемой, а ее размерность совпадает

с порядком передаточной функции системы.

обозначим порядки (размерности) подсистем через n

, n

соответственно. для их вычисления надо выписать матри-

цы управляемости и наблюдаемости, а также их произведение

H = DR и найти их ранги. имеют место следующие простые соот-

ношения:

01 02 0

rank rank rank, ,.nn nn n=+ =+ =RDH

из них и

194

равенства n = n

+ n

получаем формулы для порядков

каждой из подсистем:

01 2

rank rank rank rank rank,,,nn n= =- =-H RH HD

rank rank rank .nn=+ - -HRD

(6.11)

Пример 13. Проанализируем минимальность системы третье-

го порядка

011

101 0 001

110

, [ ].uy

éù

êú

= +=

êú

ëû



XX X

Решение. выписываем матрицы управляемости и наблюдае-

мости:

1 02 001

0 1 1 110

011 112

é ù éù

ê ú êú

ë û ëû

так как |R| = |D| = 0, то система неуправляема, ненаблюдаема

и неминимальна.

определим порядок минимальной реализации:

( )

225

rank rank 2 2 2 2

222

éù

êú

== =

êú

ëû

чтобы найти минимальную реализацию, перейдем к переда-

точной функции. используя для вычислений формулу (6.10), по-

лучим

11 1

1 1 1 11

11 1

() ,

()

( ) ( ) ( ).

pp p

p p pp p

p pp

pp p

∆

éù

-+ +

éù

êú

- = - - =- + - +

êú

++ -

ëû

êú

ëû

=+ -

следовательно, передаточная функция имеет вид

0 01

12 12

[]

()

() .

( )( ) ( )( )

Qp p

pp pp

éù

êú

= +=

êú

+- +-

êú

ëû

195

сокращение множителя p + 1 в числителе и знаменателе при-

водит к понижению порядка передаточной функции на единицу.

в данном случае

0 12 3

2 01, ,.n nn n= == =

следовательно, исход-

ную систему можно декомпозировать на две подсистемы: мини-

мальную реализацию размерности «два» с собственными числа-

ми 2, –1 и неуправляемую, ненаблюдаемую подсистему размер-

ности «единица» с собственным числом –1 (рис. 6.22).

s

s

Рис. 6.22. Декомпозиция Калмана для примера 13

Упражнение 8. система пятого порядка описывается матри-

цами:

10000 4

1 0001 12

0 1000 21

00001

0 0 1 0 0 30

0 0 0 1 0 23

, , [ ].

é ù éù

ê ú êú

= ==

ê ú êú

ë û ëû

A bc

найти ее каноническую декомпозицию калмана и минималь-

ную реализацию.

Ответ. ранг матрицы управляемости равен 4, т. е. имеет-

ся неуправляемая подсистема первого порядка. ранг матри-

цы наблюдаемости равен 5, т. е. система наблюдаема. кано-

ническая декомпозиция калмана содержит две подсистемы:

0 1 23

41 0,, .n n nn= = ==

Минимальную реализацию получаем,

выписав передаточную функцию

1 23 16 7 16

1 11

( )( )

()

( ) ( )( )

p p pp

ppp

- + ++

+ +-

и сократив числитель и знаменатель на общий множитель р –1.

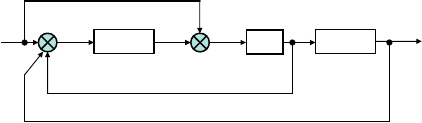
Пример 14. Проанализируем минимальность системы третье-

го порядка, блок-схема которой приведена на рис. 6.23.

196

Q

Q

Q

s



s





Z

Рис. 6.23. Блок-схема системы для примера 14

Решение. описание системы в пространстве состояний имеет

вид:

1 12 3

3 23

x xx x

x xu

x xx

=- - +



[ ]

1 11 1

1 0 0 1 001

01 1 0

,, .

é ù éù

ê ú êú

= =- =

ê ú êú

ë û ëû

A bc

Проверяем управляемость, наблюдаемость и минимальность:

>>s = ss(A,b,c,0); R = ctrb(s); D = obsv(s); rank(R), rank(D), minreal(tf(s))

R = ctrb(s) D, tf = obsv(s) minreal(tf(s))

1 0 -2

-1 1 0

0 -1 2

rank(R) = 2

0 0 1

0 1 -1

1 -1 1

rank(D) = 3

-1

-----------------

s^2 + 2s + 2

следовательно, система неуправляема, наблюдаема, немини-

мальна. Порядок минимальной реализации равен двум.

6.7. Анализ демографической модели

Почти все полученные результаты по управляемости и наблю-

даемости непрерывных систем оказываются справедливыми и

для систем с дискретным временем, описываемых уравнениями

1( ) () (), () ().k k uk yk k+= + =X AX b cX

(6.12)

для них точно так же вводятся понятия управляемости и на-

блюдаемости; матрицы управляемости и наблюдаемости стро-

ятся по формулам (6.5), (6.7); критерии управляемости, наблю-

даемости и минимальности имеют тот же вид. исключение со-

ставляют грамианы управляемости и наблюдаемости, которые

вычисляются по другим формулам.

Проиллюстрируем применение изложенной теории на при-

мере анализа наблюдаемости дискретной модели, описывающей

структуру населения в некотором регионе.

197

При анализе структуры населения города или страны ис-

пользуются различные демографические модели. в частности,

модель возрастной структуры отражает распределение числен-

ности населения по годам. если при этом еще учитывается и пол,

то говорят о половозрастной (или возрастно-половой) структуре.

графически модели возрастной структуры изображаются в виде

так называемых демографических пирамид, где по оси абсцисс

откладывается численность каждой из возрастных групп, а по

оси ординат – возраст соответствующей группы.

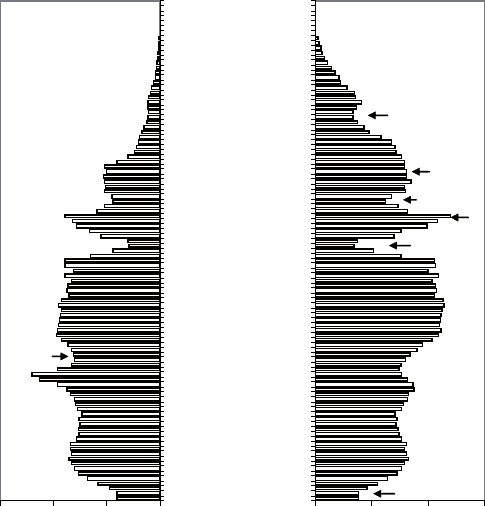
Пример такой демографической пирамиды, характеризую-

щей структуру населения санкт-Петербурга в 1995 году, приве-

ден на рис. 6.24. Левая часть пирамиды соответствует мужскому

населению города, правая – женскому. в пирамиде нашли отра-

жение результаты войны и блокады (возраст 50–54 лет), а также

Рис. 6.24. Структура населения Санкт-Петербурга (1995 г.)

¥Ì¿ÐÁÆÔ



Ç¼Ç½¹







































ÇÀÉ¹ÊË

°ÁÊÄ¾ÆÆÇÊËÕÐ¾Ä

¾ÆÒÁÆÔ

   







































ÁÊË¹ÉÑ¾

É¹¿½¹ÆÊÃ¹Ø

»ÇÂÆ¹s



¦¶¨

ÇÄÇ½

¼

Ä¹¼ÇÈÇÄÌÐÆÔ¾

ÈÉ¾½»Ç¾ÆÆÔ¾

¼Ç½Ô



ÇÂÆ¹

s



©¹ÊÈ¹½

ªªª© 

¶ÎÇ»ÇÂÆÔ

Ð¾É¾À

¼Ç½¹

¼¼

198

так называемое «эхо войны» – уменьшение численности детей,

родители которых были рождены во время войны (возраст 26–30

лет). видно также резкое снижение рождаемости после распада

ссср.

для построения таких пирамид проводят специальные со-

циологические исследования, в процессе которых производятся

длительные наблюдения за одной или несколькими возрастны-

ми группами. в связи с этим возникает вопрос информативности

данных о той или иной группе для построения всей демографиче-

ской пирамиды, поскольку это напрямую связано с финансовы-

ми затратами на социологическое исследование.

Перейдем к математической формулировке этой задачи. Пусть

все население разбито на n возрастных групп. обозначим через

, …, x

численность мужских групп, а через у

, …, у

– чис-

ленность женских групп. тогда вектор

[ ]

, …, , …, ,

x xy y=X

будет полностью характеризовать половозрастную структуру

населения. допустим, у нас имеется возможность наблюдать за

численностью только одной группы. спрашивается, за какой из

групп следует наблюдать, чтобы на основе этих данных могла

быть определена численность всех остальных групп. Мы получи-

ли стандартную задачу анализа наблюдаемости.

чтобы упростить рассуждения, примем n = 3, т. е. будем рас-

сматривать три мужские возрастные группы (назовем их условно

– «мальчики», x

– «отцы», x

– «дедушки») и три женские

группы (у

– «девочки», у

– «мамы», у

– «бабушки»).

обозначим a

, b

вероятности рождения мальчиков и дево-

чек мамами i-й возрастной группы; p

, q

– вероятности дожи-

тия членами i-й возрастной группы до перехода в следующую

группу.

тогда в первом приближении динамика изменения числен-

ности может быть описана следующей линейной моделью с дис-

кретным временем:

1 11 22 33

2 11

3 22

( ) () () (),

( ) ( ),

( ) ( ).

xk aykaykayk

yk byk byk byk

x k px k

y k qy k

x k px k

y k qx k

+= + +

(6.13)

199

Перейдем к матричной форме записи:

1 23 1

0 00

0 0 000

0 0 0 00

( ) ( ), ,

k ky

a aa x

b bb y

+= =

é ù éù

ê ú êú

ë û ëû

X AX CX

вектор-строка с определяет выбор наблюдаемой группы и мо-

жет принимать одно из шести значений:

[ ] [ ] [ ]

1 23

4 56

100000 010000 001000

000100 000010 000001

, ,,

, ,.

= ==

C CC

(6.14)

для каждого из шести вариантов надо построить матрицу на-

блюдаемости и определить ее ранг. нас интересуют только те

группы, у которых ранг равен 6. если же таких групп не окажет-

ся, то задача в поставленной формулировке решения не имеет.

найдем матрицу наблюдаемости для первого варианта (на-

блюдение за текущей численностью мальчиков):

1 23

11 21 12 3 2 13

1 0 0 0 00

00 0

a aa

ab aq ab aq ab

éù

êú

´ ´´

êú

´ ´´

êú

´ ´´

êú

ëû

êú

ëû

Мы видим, что независимо от значений элементов, обозначен-

ных крестиками, матрица D

вырождена, так как в ней имеются

нулевые столбцы:

0 rank 4det , .==DD

следовательно, группа

мальчиков неинформативна: наблюдая за ней, нельзя опреде-

лить численность остальных групп. Аналогичный вывод получа-

ем, находя матрицу наблюдаемости для группы девочек, а также

«мам» и «пап».

200

остается надежда на старшие возрастные группы («дедушек»

и «бабушек»). вычисление матриц наблюдаемости для них дает:

112 212 312

11 21 12 12 32 12 1312

62 64 66

0 0 0 0 10

0 0 0 00

0 00

( )( )

app app app

ab aq p p ab aq p p ab pp

d dd

éù

êú

ëû

где d

11 21 211 31212

(( ) )ab bq abq aqq pp+++

112 32 22112

(( ) )abb bq abqpp++

112 32 22112

(( ) )abb bq abqpp++

311 2112

()babaqpp+

112 212 312

000001

000 00

0 0000

000

bqq bqq bqq

éù

êú

´´´

êú

´´´

êú

ëû

Матрица D

содержит три нулевых столбца, т. е.

rank 3.=D

следовательно, группа «бабушек» еще менее информативна, чем

группа «мальчиков». и только матрица D

оказывается невы-

рожденной – ее определитель в общем случае отличен от нуля.

чтобы доказать это, преобразуем матрицу D

. Перестановкой

столбцов она приводится к блочно-диагональному виду

éù

êú

ëû

здесь F, G – матрицы третьего порядка:

10 0

éù

êú

ëû

1 23

11 2 1 12 3 2 13

1 12 32 132 221 132 213

()

a aa

ab aq ab aq ab

q ab aq abq abq baq aqb

éù

êú

=+ +

êú

+ +-

ëû