Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

181

можным, если указки одинаковы. но если указки разной длины,

задача их удержания на ладони в принципе разрешима!

Упражнение 3. Проанализировать управляемость пары обыч-

ных маятников. Показать, что ответ полностью аналогичен: си-

стема управляема, если маятники разной длины.

Упражнение 4. Проанализировать управляемость системы из

n перевернутых маятников. Показать, что система управляема,

если все маятники разной длины.

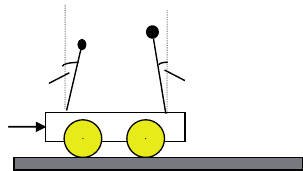
рассмотрим усложненный вариант предыдущей задачи, ког-

да необходимо учитывать массу основания. Пусть теперь речь

идет об управлении массивной тележкой с двумя перевернутыми

маятниками на платформе (рис. 6.14). динамика объекта описы-

вается системой линейных дифференциальных уравнений с ма-

трицами

1 1 21

12 2 2

010000

00 0 0

00 0 1 0 0

0 01 0 0

000001

0 0 01 0

( / )/ /

/ ( / )/

mgM mgM

m Mgl mglM

mglM m Mgl

æö

èø

æö

èø

Рис. 6.14. Перевернутые маятники на тележке

























182

где М, m

, m

– массы тележки и маятников; l

, l

– длины

маятников; g – ускорение свободного падения. вектор со-

стояния X включает в себя шесть составляющих: положение

и скорость тележки, угловые положения и угловые скорости

каждого маятника.

возможны две постановки задачи:

– стабилизация только маятников;

– стабилизация маятников и тележки.

оказывается, в обоих случаях система управляема, т. е. ста-

билизация возможна, если маятники имеют разную длину.

Упражнение 5. Проанализировать управляемость и наблю-

даемость этой системы для обоих вариантов постановки задачи.

заметим, что при первой постановке задачи уравнение тележки

удается исключить и понизить размерность задачи до четырех.

6.4. Анализ наблюдаемости

наблюдаемость характеризует возможность определения со-

стояния системы по наблюдениям за ее выходными сигналами.

рассмотрим линейную динамическую систему, заданную описа-

нием в пространстве состояний (6.4) при

0() :ut =

0, , () .y== =



X AX cX X X

(6.6)

о п ре д е л е н и е . система называется наблюдаемой, если,

измеряя выходной сигнал y(t) в течение конечного времени Т,

можно однозначно определить ее начальное состояние Х(0). если

хотя бы для одного

RÎX

это сделать невозможно, система на-

зывается ненаблюдаемой

заметим, что в этом определении можно заменить начальное

состояние Х(0) на конечное состояние Х(Т) = Х

. действительно,

если состояние Х(0) найдено, то состояние Х

можно рассчитать

по формуле

X eX

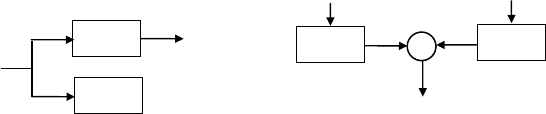
Рис. 6.15. Ненаблюдаемые структуры





 4



V

Z

 4









 4









Z

б)

а)

183

Простые примеры ненаблюдаемых систем приведены на рис.

6.15, а, б.

в первом случае (рис. 6.15, а) часть переменных состояния не

влияет на выходной сигнал. во втором случае (рис. 6.15, б) мы

имеем две одинаковые подсистемы, и невозможно отличить их

вклад в выходной сигнал (наиболее показательна ситуация, ког-

да начальные условия одной из подсистем равны нулю).

Прямой способ анализа наблюдаемости сводится к получению

системы уравнений для определения неизвестных начальных

условий и проверке ее разрешимости.

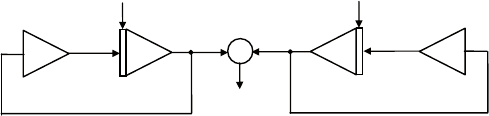
Пример 8. схема моделирования, приведенная на рис. 6.16,

содержит два интегратора, охваченных обратной связью, и сум-

матор для получения выходного сигнала

.yx x=+















Рис. 6.16. Схема моделирования для примера 8

для анализа наблюдаемости используем выражения для сиг-

налов

, ,:xxy

1 2 12

, , () .

kt kt kt kt

x ae x be y t ae be= = =+

запишем последнее равенство для двух моментов времени,

например для t

= 0 и t

= 1:

01( ), ( ).

a b y ae be y+= + =

Мы получили систему двух уравнений с двумя неизвестными

начальными условиями а и b:

()

éù

éù é ù

êú

êú ê ú

êú

êú ê ú

êú

ëû ë û

ëû

она разрешима, если определитель системы не равен нулю

ee-¹

следовательно, при k

≠ k

схема наблюдаема, а при

= k

– нет.

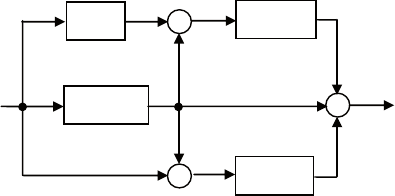
Пример 9. Проанализируем наблюдаемость электрической

схемы, приведенной на рис. 6.17, при следующих значениях па-

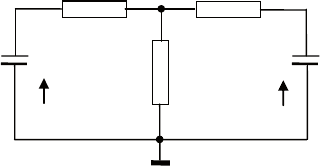
184

раметров: С = 1, r = 1, R = 2. в качестве переменных состояния

примем напряжения х

, х

на конденсаторах, измеряемый сиг-

нал – напряжение в точке у.

Процессы в электрической цепи описываются уравнениями:

( )

11 22 1 1

2 2 12

, , /,

/ , /, / .

x iz x iz i x y R

i x y R i i y r z pC

=× =× = -

= - += =

Подставляя сюда числовые значения параметров и выполняя

элементарные преобразования, получаем:

1 1 2 2 12

22 4,,.x yx x yx y x x=- =- = +



сложим два первых уравнения с учетом третьего:

4 .yy=-



ре-

шение этого дифференциального уравнения имеет вид:

( )

0 10 20

0 25,( ) .

yt ye x x e

== +

таким образом, измеряемый сигнал у зависит от суммы на-

чальных условий, т. е. не будет меняться при перераспределе-

нии начальных условий (при сохранении их суммы). отсюда

следует невозможность однозначного восстановления началь-

ных условий по наблюдению за сигналом y(t), т. е. ненаблюдае-

мость схемы.

к этому результату можно было прийти более коротким пу-

тем, не прибегая к решению дифференциальных уравнений.

для доказательства ненаблюдаемости достаточно указать хотя

бы одно сочетание начальных условий, которое невозможно вос-

становить. Простой пример получаем, взяв х

= –х

, тогда из

схемы видно, что напряжение y(t) = 0 в любой момент времени.

такой выходной сигнал не несет никакой информации о процес-

сах в схеме, следовательно, она является ненаблюдаемой.

Рис. 6.17. Электрическая схема

3

Z

S

$











185

Упражнение 6. Проанализируйте поведение схемы при рав-

ных начальных условиях х

= х

. воспользуйтесь симметрией

схемы и соедините эквипотенциальные точки х

(при этом

резисторы R и конденсаторы С окажутся включенными парал-

лельно).

Последний пример показывает, что для анализа наблюдае-

мости не обязательно исследовать динамику системы, а можно

ограничиться алгебраическими выкладками. наиболее извест-

ный алгебраический критерий основан на анализе матрицы на-

блюдаемости D, которая имеет вид

...

éù

êú

ëû

(6.7)

если у системы s выходов, эта матрица имеет ns строк и n

столбцов. в пакете MATLAB матрицу наблюдаемости можно

найти с помощью команды obsv.

для того чтобы система (6.6) была наблюдаемой, необходи-

мо и достаточно, чтобы матрица наблюдаемости имела полный

ранг: rankD = n.

в случае систем с одним входом анализ ранга может быть за-

менен вычислением определителя (для наблюдаемости опреде-

литель должен быть отличен от нуля detD ≠ 0).

таким образом, наблюдаемость системы определяется свой-

ствами пары матриц А, с.

Пример 10. объект управления задан структурной схемой

(рис. 6.18), где Q

(p) = 1/(p + a

), Q

(p) = a

/(p + a

Рис. 6.18. Блок-схема для примера 10

 



Q 



Q 



Q 













V

Z

186

требуется проанализировать его управляемость и наблюдае-

мость.

Решение. Принимая выходные сигналы блоков за переменные

состояния, перейдем к матричному описанию:

= + u,



X AX b

y = cX,

где X∈R

– вектор состояний; u, y – входной и выходной сигналы.

Постоянные матрицы A, b, c имеют вид:

[ ]

0 0 111

01 1

,, .

é ù éù

ê ú êú

=- ==

ê ú êú

ë û ëû

A bc

находим матрицы управляемости и наблюдаемости

2 12 3 1 2 13 23

3 23 23

3 1 1 13 23

a aa a a a aa aa

a aa aa

aa aaaaa

éù

-+ --

êú

- --

êú

ëû

1 21

1 1 22 1

111

()

a aa

a a aa a

éù

êú

=- - -

êú

- --

ëû

вычисляем определители: det(R) = 0, det(D) = 0. следователь-

но, система неуправляема и ненаблюдаема при любых а

, а

Пример 11. Проанализируем управляемость и наблюдаемость

системы, структурная схема которой приведена на рис. 6.19, а.

Способ 1 (анализ передаточной функции). Пользуясь схемой,

выпишем передаточную функцию

( )

3 1 21 1

1 2 12 1

p p pp p

æö

=+ = =

+ - +- +

èø

Произошло сокращение одинаковых множителей числителя

и знаменателя. это означает, что система либо неуправляема,

либо ненаблюдаема, либо то и другое одновременно.

найдем фазовую траекторию системы в плоскости сигналов

, х

. для этого запишем операторные выражения для этих сиг-

налов:

( ) ( )

( ), ( ).x p up x p up

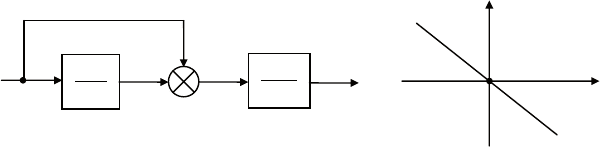
187

из них следует равенство:

30.xx+=

Мы получили уравнение прямой линии. если при t = 0 изо-

бражающая точка была в начале координат, то далее она сможет

двигаться только по этой прямой (рис. 6.19, б). следовательно,

система неуправляема.

для анализа наблюдаемости положим и = 0 и запишем равен-

ства

2() (); ()( ) (),yp x p yp p x p= -=

откуда

2() (), () () ().x t yt x t yt yt= =-



эти формулы позволяют оценить значения переменных x

(t),

(t) в любой момент времени, в том числе и при t = 0. следова-

тельно, система наблюдаема.

Способ 2 (анализ матриц управляемости и наблюдаемости).

Перейдем от схемы (см. рис. 6.19, а) к описанию в пространстве

состояний

( )

2 ,p xxu- =+

( )

13.px u+ =-

После несложных преобразований получаем

1 12

2 ,x xxu= ++



22 1

3 ;.x x u yx=- - =



выписываем матрицы А, b, с и матрицы управляемости и на-

блюдаемости R, D:

Рис. 6.19. Пример неуправляемой системы









s









Qs



À

Ë





б)

а)

188

[ ]

2 1 1 1 1 10

0 1 3 3 3 21

,, , , .

é ù éù é ù é ù

ê ú êú ê ú ê ú

= == = =

ê ú êú ê ú ê ú

-- -

ë û ëû ë û ë û

A bc R D

вычисляем определители матриц R, D:

01;.==RD

следовательно, система неуправляема, но наблюдаема.

6.5. Грамианы управляемости и наблюдаемости

другой способ проверки управляемости и наблюдаемости си-

стемы (6.4) опирается на вычисление грамианов управляемости

и наблюдаемости. так называются симметричные квадратные

матрицы W

и W

, определяемые равенствами

dd,.

t t tt

¥¥

òò

AA A A

W e bb e W e c ce

(6.8)

в пакете MATLAB их можно найти с помощью команд типа

gram(sys, ‘c’), gram(sys, ‘o’). их первый входной аргумент – имя систе-

мы, второй – опция ’c’ или ’о’ (от controllability и observability).

необходимым и достаточным условием управляемости и на-

блюдаемости служит невырожденность этих матриц: det W

≠ 0,

det W

≠ 0.

грамианы W

и W

удовлетворяют матричным уравнениям

Ляпунова

T T TT

c c oo

+ =- + =-W A AW bb W A A W c c

наряду с грамианами управляемости и наблюдаемости рас-

смотрим кросс-грамиан W

(определен только для скалярных

систем)

W e bce

(6.9)

кросс-грамиан, в отличие от грамианов управляемости и на-

блюдаемости, в общем случае не является симметричной матри-

цей, однако все его собственные числа вещественны.

он удовлетворяет матричному уравнению Ляпунова

co co

+ =-W A AW bc

для решения уравнений Ляпунова в

MATLAB существует команда lyap. команда для вычисления

кросс-грамиана

будет иметь вид

=W AAb clyap( , , * ).

для

189

контроля вычисления грамианов

удобно использо-

вать связывающее их соотношение

co c o

=W WW

кросс-грамиан отражает как свойства управляемости, так

и свойства наблюдаемости системы. из равенства

co c o

=W WW

следует, что

( )

det det det ,

c o co

=WW W

т. е. вырожденность лю-

бого из грамианов

или

приводит к вырожденности

Поэтому наличие ненулeвого определителя

0det

¹W

является

критерием одновременной управляемости и наблюдаемости си-

стемы.

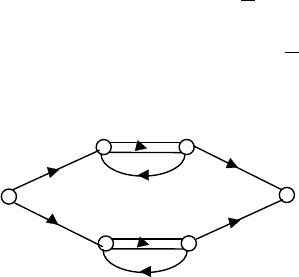
Пример 12. исследуемая система, содержащая два парал-

лельно включенных апериодических звена, задана сигнальным

графом (рис. 6.20).

чтобы найти ее грамианы управляемости и наблюдаемости,

перейдем к описанию в пространстве состояний. оно характери-

зуется матрицами

[ ]

10 3

02 3

,, .

é ù éù

ê ú êú

= ==

ê ú êú

ë û ëû

A bc

для вычисления грамианов нам потребуются матрицы

,, .

t t ttt

é ù éù

ê ú êú

éù

= ==

ê ú êú

êú

ëû

ê ú êú

ë û ëû

A AA

e e b ce

Подставляем их в формулы (6.8):

éù

êú

éù

êú

ëû

êú

ëû

Рис. 6.20. Сигнальный граф для примера 12

V

Z













s

s

s

190

éù

êú

éù

êú

ëû

êú

ëû

определители грамианов отличны от нуля, поэтому система

управляема и наблюдаема.

Упражнение 7. найти кросс-грамиан системы и прямой под-

становкой проверить, что грамианы удовлетворяют трем уравне-

ниям Ляпунова.

все три грамиана, введенные выше, существуют только для

устойчивых систем. При анализе неустойчивых систем возника-

ет необходимость вычисления грамианов

( ),

()

для конечного интервала времени T. они определяются форму-

лами вида (6.8), (6.9), в которых бесконечный верхний предел

интегрирования заменен на конечный предел T. это приводит

к изменению уравнений Ляпунова, которые принимают вид

T T TT

() () ,

TT+ =- +W A AW BB FBB F

T T TT

() ()

TT+ =- +W A AW CC FCCF,

() () ; .

co co

TT+ =- + =

W A AW bc FbcF F e

для решений этих уравнений может быть использован опера-

тор MATLAB lyap. Поясним это на примере вычисления кросс-

грамиана:

* * ***

F=expm(A T); W =lyap(A, A, b c–F b c F).

если нужно вычислить значение грамианов устойчивой си-

стемы для серии различных интервалов времени T, то удобнее

воспользоваться формулами

() , () ,

c c o co

TT=- =-W W FW F W W FW F

() ,

co co co

T =-W W FW F

связывающими значения грамианов на конечном и бесконечном

интервалах времени.

Подведем итоги анализа управляемости и наблюдаемости.