Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

3 Hologram Simulation of the FKNME 

  Chi Mei and Zhuo Chen

3.3



Applying Hologram Simulation to Multi-field Coupling

Hologram simulation strategy requires a complete (or at least as complete as possible)

coverage of all physical and chemical processes involved. Mathematically this

requirement is satisfied by simultaneously establishing and solving the equation set

governing all of these processes (refer to Table 3.2). Such an approach indeed brings

the impression that the simulations are of “hologram-style”. This is, however, not

enough to make sure that the simulations are capable of revealing the inherent

mechanisms of the interactions among the processes, which is actually the true

essential element making the simulation holographic. These interactions among

different processes are often referred to as the coupling effects. The crucial task and

the key indicator of hologram simulation are the insightful understanding and

quantitative assessment of these coupling effects in the physical and chemical

processes, which we call the “multi-field coupling”.

3.3.1 Classification of multi-field coupling

The multi-field coupling problems may be classified as follows (Table 3.3).

Table 3.3 Overview of multi-field coupling problems

Classification indicator Class Examples

Coupling in the same phase

Between velocity field and scalar

fields in the same fluid phase

The range of coupling

Coupling between two or

among more phases

Between fluid and particles phase

Linear coupling (convection

term, source term)

Simple coupling of time averaged

(or steady-stated) variables

The mechanism of

Coupling

Fluctuation coupling

(turbulent diffusion, source

term)

Coupling terms

(

;uu c n m T

ij j

′′ ′ ′ ′

) consisting of

two or more fluctuation variables

Bidirectional coupling

(simple interaction)

Buoyancy vs flow field and

temperature field

Loop-wise coupling Refer to Fig. 3.1

Fluctuation coupling

The strong non-linear correlation

of the second and(or) the third

order fluctuations, chaotic

phenomena

The patterns of

interaction

Multidirectional coupling Refer to Fig. 3.2

3 Hologram Simulation of the FKNME 

Continues Table 3.3

Classification indicator Class Examples

Explicit coupling Multivariable correlating terms

The formulation of the

model

Implicit coupling

Model parameters such as

turbulent viscosity or transport

coefficients

3.3.2



An example of intra-phase three-field coupling

The freeze profile of an aluminum reduction cell is a good example of the

intra-phase coupling(Mei et al., 1986; Mei et al., 1997).

The profiles are the

direct result of the cathode temperature field, but also are strongly influenced by

the melting mass flow field, the current field and the magnetic force field. The

interactions of the fields are described by the energy equation and the momentum

equation of the molten mass:

Energy equation:

()

eff

jjj

uT a

xxxc

⎛⎞

′

∂∂∂

⎜⎟

∂∂∂

⎝⎠

(3.1)

Momentum equation:

()

eff Bj

jjjji

uu F

xxxxx

ρρ

⎡⎤

⎛⎞

∂

∂∂∂

=− + + +

⎢⎥

⎜⎟

∂∂∂∂∂

⎢⎥

⎝⎠

⎣⎦

(3.2)

where the magnetic force is:

Bj ik

JB=×, in which J

is the horizontal current in

the cell, and

is the vertical magnetic induction intensity; a

eff

is the effective

thermal diffusion coefficient,

eff

=a+a

(3.3)

eff

is the effective kinematic viscosity,

eff

(3.4)

and v

are respectively the turbulent diffusion coefficient and turbulent

kinematic viscosity.

The temperature filed in the cell determines the profile and the size of the

cell, which influences the horizontal current. The horizontal current then

influences the electro-magnetic force on the horizontal plane. Represented by

the source term in Eq. 3.2, the horizontal electromagnetic force drives the

horizontal movement of the melt, which affects not only the temperatures in

the melt but also the turbulent thermal diffusion coefficient. In other words,

the heat transfer and temperature distribution in the melt are impacted by the

velocities through the parameter

eff

. Note that a

in Eq. 3.3 and v

in Eq. 3.4

satisfy the equation:

  Chi Mei and Zhuo Chen

= (3.5)

where

Pr is the turbulent Prandtl number (also referred to as

in literatures),

which is an experimental constant. Usually

is computed through the standard

− model (or low Reynolds number k

− models):

= (or at small Re:

μμ

= )

So:

1 k

Pr Pr

== or

1 k

aCf

μμ

= (3.6)

The turbulent kinetic energy k of the melt phase influences the flow field and

the temperature field with the same order of magnitude. The parameters a

eff

andµ

eff

can be considered as two terms of intra-phase “implicit coupling”.

The couplings of the flow field, the temperature field and the magnetic force

field in the melt phase are realized through the convection term u

T, the diffusion

term

eff

∂

and the source term

. Such an intra-phase three-field coupling

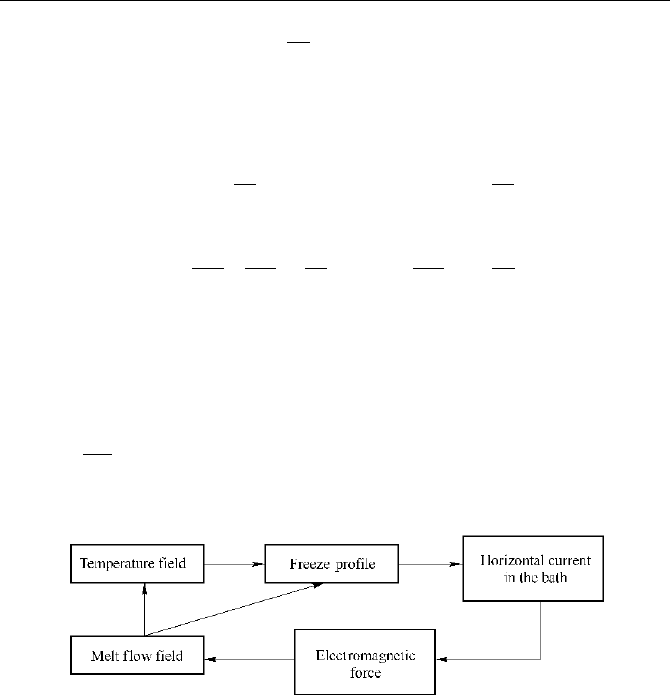
can be schematically illustrated in Fig. 3.1.

Fig. 3.1 The coupling of temperature field, flow field and magnetic force field

in aluminum reduction cell

Note the source term

′

in Eq. 3.1, which is the Joule heat generated by

current. Apparently, all variables and processes that may influence the current

distribution should have direct influences on the melt temperature. As mentioned

above, the temperature field also influences the current distribution through the

freeze profile. Therefore the current field and the temperature field is actually an

example of bi-directional intra-phase coupling.

3.3.3



An example of four-field coupling

In the generalized fluidization system with dilute-phase chemical reactions (such as

the flash smelting, alumina hydroxide calcinations and pulverized coal combustion),

the momentum equation of the gas phase is (Zhou, 1994; Cen and Fan, 1991):

3 Hologram Simulation of the FKNME 

()

()/

iij ikkiirk

ijiijjiij

kki

uuu g

tx xx

vS F vv v v v v vv

ρρ ρ

ρρρρ

ρτ

∂

∂∂ ∂

+=−++Δ+

∂∂ ∂∂

∂

′ ′ ′′ ′′ ′′′

+− +++

∂

′′

−+

∑

()

ki i k k k i k

kkki ik k

nv v vm nvm

mnv vnm

′′ ′ ′ ′ ′

−−

′′′ ′′ ′

−−

−

∑∑

For the particle phase, the momentum equation is written as:

()

(

) ( ) (

k ki k kj ki i i k i ki k kj ki

jrkkkj

kj k ki k kj ki k i k ki rk i k k

nv nvv n

nv v nvv

tx mmx

v nv nv v nv nv vnm

⎛⎞

∂∂ ∂

′′

+=+−++−+

⎜⎟

∂∂ ∂

⎝⎠

′′ ′′ ′ ′′ ′′ ′ ′

++− ++

•

()

) /

ki k k ki ki k ki k k k ki k

kkki kki k k kki

nvm mnv nvm v nm nvm

mnv nvm m nv

′ ′ ′′ ′′ ′ ′ ′ ′ ′

++−−−

∂

′′ ′′ ′ ′′

−−

∂

&& & & &

(3.8)

The energy equation for the gas phase is:

()

jrkkkk

jjj

kk k kk k k

jj j j

v n hs h n m

tx xx

nhm mn h nm

hh qQ

vh v h h v hv

ρλ

ρρρρ

∂∂ ∂∂

′′

+= +−

∂∂ ∂∂

∂

′′ ′ ′′

∂

⎛⎞

−+ −

⎜⎟

⎝⎠

′′′

−−−−

′′ ′′ ′′ ′′′

+++

∑∑

∑∑ ∑

&& &

(3.9)

The energy equation for the particles phase is:

()

()(

) (

kk kkj kk k h k rk k p kk

j k

kkk kkkjk kkjkk

kk kkj k kjkk p k k k k

kk pkk k kkkk

kkk k k kk

nkCT nv CT n Q Q Q m CT CT

tx m

CnT nCvT Cv nT

CTnv C v nT CTnm C nm

CmTn CnmT m CTnm

CnTm CmnT

∂∂

+=−−+−−

∂∂

′′ ′ ′ ′′

−× + +

∂∂

′′ ′ ′ ′ ′ ′ ′ ′

+++

′′ ′ ′ ′ ′ ′

′′ ′′

−

&& &

)

kkkkk k

CnmT m

′′′

(3.10)

The species equation for the gas phase is:

(3.7)

  Chi Mei and Zhuo Chen

()

(

) ()

sjs sskkjs

jjj j

jjs js skk s

YvYD nmvY

tx xx x

Yv vY vY nm Y

ρρ ρωα ρ

ρρρ α ρ

∂

∂∂ ∂ ∂

′′

+= −+ +

∂∂ ∂∂ ∂

∂

′′ ′ ′ ′′ ′ ′ ′ ′ ′

++ − −

∂

⎛⎞

−

⎜⎟

⎝⎠

(3.11)

where

is the source term of reactions and can be described by Arrhenius law:

exp

ωρ

∑

=−

∏

⎛⎞

⎜⎟

⎝⎠

(3.12)

From Eq. 3.7 to Eq. 3.12, the subscript k denotes variables pertaining to the

particles phase, subscript S denotes species components, and n denotes density

measured by particle numbers. Q

, Q

and Q

represent respectively the reaction

heat flux, convection heat flux and radiation heat flux. The symbols m,

, S,

and Y stand for mass, mass change rate, mass source, Magnus force and

species concentration (percentage). And

is the excess air ratio, D is the

diffusion coefficient,

is the fluid viscous stress, and

is the particle

relaxation time.

The set of Eq. 3.7 to Eq. 3.12 describes the velocities, temperatures, species,

concentrations and reaction rates of both the gas and particles phases. The

following conclusions can be drawn based on the equation set:

a) The momentum, energy, species and reaction rates are intensively interacting

between the gas phase and the particles phase (the reaction rates are referred

specifically to the exothermic heat rate in sulfide roasting or pulverized coal

combustion cases). Their coupling process is illustrated in Fig. 3.2.

Fig. 3.2 Four-field coupling mode

b) The coupling effects are chiefly represented by the source terms in the

governing equations.

c) Implicit coupling also exists. For instance, the term

′′

from Eq. 3.7 to

Eq. 3.11 represents the influences of gas turbulence on the flow, temperature,

3 Hologram Simulation of the FKNME 

concentration and endothermic reaction heat fields of the particle phase. In the

case of vaporization of liquid drops and combustion of coke particles, this

second-order correlation of fluctuation is modeled as: (Zhou, 1994; Cen and Fan,

1991)

kk m k

jj p

nm C dNu

xx c

∂

′′

∂∂

(3.13)

or:

kk m k

nm C dD

∂∂

′′

∂∂

(3.14)

The above equations indicate that the mean particles reaction rates will be

intensified by the increasing turbulent kinetic energy and dissipation, as well as

the gas temperature and oxygen concentrations. Meanwhile the intensified

particles reaction rates will in return more remarkably influence the flow,

temperature and concentration field of the gas and particles phases.

3.4



Solutions of Hologram Simulation Models

Coupling effects often bring about problems to numerical convergence. Usually

the stronger the effects, the more difficult the numerical convergence.

The equation set is usually solved either by a direct iteration or by a multi-level

iteration. For a simple linearly coupling equation group, direct iteration is enough.

In the complex situation with strong nonlinearly coupling effects, however, a

multi-level iteration is needed. This iteration technique involves an

“iteration-updating-resuming iteration” loop scheme (Mei et al., 1996; Zhou et al.,

1990; Zhou et al., 1997; Mei et al., 1998).

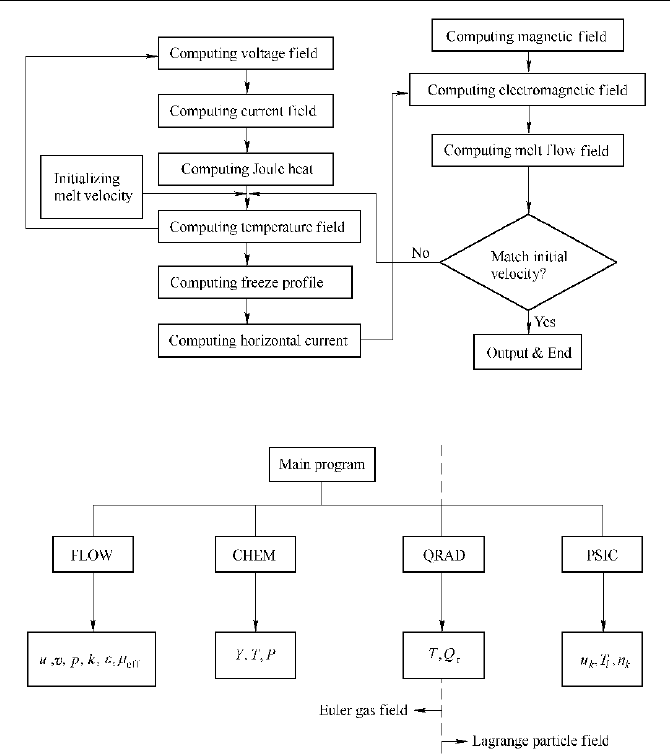
The solving process for the six-field coupling problem of an aluminum

reduction cell is a good example of the multi-level iterations. As shown in Fig. 3.3,

iterations have to be implemented not only within each particular field but also

among different fields.

The computation of dilute-phase reactions in the gas-particle two-phase flow

is very complicated. J.J.Wormeck worked out a modulized, general-purpose

software package consisting of four modules (Cen and Fan, 1990; Wormeck and

Partt, 1976). The first three are Euler method based gas flow module (FLOW),

gas combustion module (CHEM) and radiation module (QRAD). The last one is

a Lagrangian method based module (PSIC) dealing with particle velocities,

trajectories, concentrations and temperatures etc.(Fig. 3.4). The four modules

communicate with each other during the iterations until the computation is

convergent.

  Chi Mei and Zhuo Chen

Fig. 3.3 Solution of six-field coupling in an aluminum reduction cell

(Mei et al., 1986; Mei et al., 1997)

Fig. 3.4 Flow chart of Wormeck’s four-module model

References

Cen Kefa, Fan Jianren (1990) Engineering Theory and Computation of Gas-solid

Multi-phase Flow (in Chinese). Zhejiang University Press, Hangzhou

Cen Kefa, Fan Jianren (1991) Combustion Fluid Dynamics (in Chinese). China Water

Power Press, Beijing

Mei Chi, Li Xinfeng, Yin Zhiyun et al (1998) Dynamic simulation of anode baking furnace

flue (in Chinese). Journal of Central South University of Technology (Natural Science),

29(5): 438

̚441

Mei Chi, Tang Hongqing, Wei Wu (1986) Mathematical model and simulated experiments

3 Hologram Simulation of the FKNME 

of electrical and heat fields in aluminum cell (in Chinese). Journal of Central South

University of Technology, (6): 29

̚36

Mei Chi, Wang Qianpu, Peng Xiaoqi et al (1996) Simulation and optimization of

nonferrous metallurgical furnaces (in Chinese). Transactions of Nonferrous Metals

Society of China, 6(4): 19

̚23

Mei Chi, Yin Zhiyun, Zhou Ping et al (1999) The hologram simulation of modern industrial

furnace and kilns

(in Chinese). Journal of Central South University of Technology

(Natural Science), 30(6): 592

̚596

Mei Chi, You Wang, Wang Qianpu et al (1997) Study and development of the simulation

software for the freeze profile in aluminum reduction cells (in Chinese). Journal of

Central South University of Technology (Natural Science), 28(2): 138

̚142

Mei Chi, Zhou Shuiliang, Wang Qianpu (1996) Mathematical simulation on electric and

temperature fields in baths of a round electric cleaning furnace (in Chinese). Journal of

Central South University of Technology (Natural Science), 27(5): 609

̚612

Wormeck J J, Partt D T (1976) Computer modelling of turbulent combustion in a Longwell

jet-stirred reactor. London: 16th Symposium on Combustion

Zhou Jiemin, Zhao Tiancong, Mei Chi (1990) Mathematical model and computer

simulation of Soderberg electrodes in electric smelting furnace. Elektrowarme

international, 48B (4): 210

̚215

Zhou Lixing (1994) Theory and Numerical Simulation of Turbulent gas-solid Two-phase

Flow and Combustion (in Chinese). Science Press, Beijing

Zhou Ping, Mei Chi, Zhou Shuiliang (1997) Numerical Simulation and Analysis on the

Velocity Field in Bath of a Round Electric Slag-cleaning Furnace. Journal of Central

South University of Technology, 4(1): 54

̚57