McMahon D. String Theory Demystified

Подождите немного. Документ загружается.

206

String Theory Demystiﬁ ed

5. In type II B theory the GSO projection can be written as:

(a)

ΓΓ

11 11

(

)

=−

(

)

left right

(b)

ΓΓ

11 11

000

(

)

(

)

left right

(c)

ΓΓ

11 11

(

)

(

)

left right

(d)

ΓΓ

11 11

(

)

(

)

−

left right

CHAPTER 12

Heterotic

String Theory

In Chap. 10, we learned that there are two string theories that treat the left- and

right-moving sectors differently. These theories are called heterotic string theories

for this reason. The modes are treated as follows:

• The left-moving sector is bosonic.

• The right-moving sector is supersymmetric.

This idea sounds nonsensical because we have learned that bosonic string theory

lives in a world of 26 space-time dimensions, while superstring theories live in a

world of 10 space-time dimensions. The reason for doing such a radical thing is the

following. First, we already know that bosonic string theories by themselves are

ﬂ awed because they do not incorporate fermions. On the other hand, type II

superstrings do not incorporate nonabelian gauge symmetries. This means that the

standard model cannot be described by superstring theory as formulated with those

theories alone. So type II theories seem to leave us with a description of the universe

208

String Theory Demystiﬁ ed

that lacks electroweak theory and QCD, an unacceptable situation since the real

world does include these interactions. One way around this problem is to add

charges to the ends of the strings, something we will discuss in Chap. 15, but in this

chapter we consider a more successful and elegant approach.

The idea of heterotic strings was originally proposed by Gross, Harvey, Martinec,

and Rohm. They proposed a theory of closed superstrings with decoupled left- and

right-moving modes that preserves the best aspects of both theories, producing a

theory which is large enough and sophisticated enough to incorporate the features

we know the theory must have to include the standard model. By making the right-

moving modes super-symmetric

• We are able to include fermions in the theory.

• We keep tachyons out of the theory, so it has a stable vacuum.

We incorporate nonabelian gauge theory in the left-moving modes. This is done

by adding Majorana-Weyl fermions

to the left-moving sector, without adding

supersymmetry. We must eliminate the extra 16 dimensions from the 26-dimension

contribution of the bosonic theory. This can be understood by discarding the view

that the extra 16 dimensions are space-time dimensions. First, note that

• The right-moving modes are supersymmetric. So, there are 10 bosonic

ﬁ elds X

among the right-moving modes.

• We keep 10 bosonic ﬁ elds

from the left-moving modes to match up

with the right-moving modes.

Since 26 = 10 + 16, we need to cancel the remaining 16 contributions from the

unwanted

present in the left-moving sector. Since the

are spinors, we need

32 of them to enable the desired calculation, hence we take

A = 132,...,

. The

symmetry group for the

is SO(32) when all of the

have the same boundary

condition. This is the SO(32) heterotic theory.

The Action for SO(32) Theory

We can write down the action as follows:

• It will include a bosonic contribution for left- and right-moving modes for

10 dimensional space-time.

• It will include fermionic spinors to add supersymmetry to the 10

dimensional space-time. These will only be rightmovers.

• It will include a contribution from the left-moving

spinors.

The ﬁ rst two pieces are familiar, we use then Majorana-Weyl fermions

which are space-time vectors like those used for worldsheet supersymmetry. So,

we have

SdXXi

2=−

′

∂∂ − ∂

∫

−+ −

πα

σψψ

()

(12.1)

The right-moving sector must incorporate supersymmetry. This is done in the

same way as in Chap. 7, we incorporate the following transformations:

δεψ δψε

µµ µ µ

Xi X==∂

−−−

and

We will add a second action to incorporate the

. This piece is similar to the

fermionic piece used in

but now we are considering left-moving modes and we

have to include all 32

. So the action is

Sdi

2=−

′

−∂

⎛

⎝

⎜

⎞

⎠

⎟

∫

∑

+−+

πα

σλλ

(12.2)

The total action for the heterotic string is therefore:

SS S

dXXi i

=−

′

∂∂ − ∂ −

∫

−+ − +

πα

σψψλ

∂∂

⎛

⎝

⎜

⎞

⎠

⎟

−+

∑

A 1

(12.3)

CHAPTER 12 Heterotic String Theory

209

Quantization of SO(32) Theory

In heterotic string theory, we describe two sectors similar to the R and NS sectors

we are already familiar with. These are

• The periodic sector P

• The antiperiodic sector A

We already know how to handle the bosonic modes and right-moving fermionic

modes included in the theory. To develop the full theory we need to quantize the

210

String Theory Demystiﬁ ed

There are no surprises here; the techniques are the same as used before. First, we

write down a modal expansion, which in the P sector is

λσ λ

Ain

e()=

−

=−∞

∞

∑

(12.4)

These are fermions, so the coefﬁ cients of the expansion

are required to satisfy

the anticommutation relation:

λλ δδ

BAB

{}

+ 0

(12.5)

The A sector, like the NS sector we are already familiar with, is similar except we

sum over half-integer quantities. We have

λσ λ

Air

e()

−

∈+

∞

∑

(12.6)

With the similar anticommutation relation

λλ δδ

BAB

{}

+ 0

(12.7)

The next step is to construct number operators for the left- and right-moving

modes, and then to use these to write down the mass spectrum. We can do this using

the NS and R sectors along with GSO projection and the super-Virasoro operators

as described in Chap. 7. Or, as we learned in Chap. 9, there are actually two ways

to describe supersymmetric modes:

• Using worldsheet supersymmetry together with GSO projection—as

applied to NS and R sectors

• Using space-time supersymmetry (the GS formalism)

In the ﬁ rst case, for the NS sector we have a number operator for the right-

moving modes:

Nrbb

Rnn

=⋅+ ⋅

−

∞

−

∞

∑∑

αα

112/

(12.8)

Let

be a physical state. The mass-shell condition for the NS sector is

0−

⎛

⎝

⎜

⎞

⎠

⎟

(12.9)

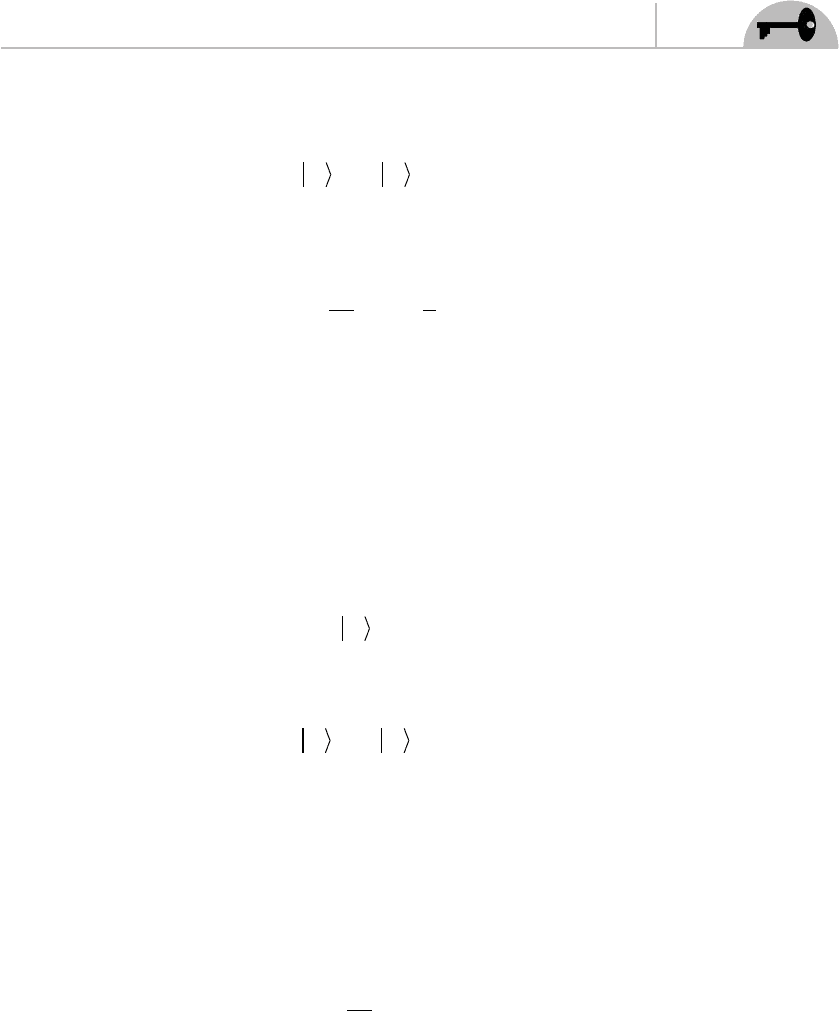
CHAPTER 12 Heterotic String Theory

211

In addition, we have the constraints

ψψ

==0

(12.10)

where r, M > 0. The operator

is given by

=+−

(12.11)

Using the Einstein relation

0−=

we have

48=−

⇒

′

=−

(12.12)

Now let’s quickly review the R sector. Once again we have a mass-shell condition,

which in this case is

(12.13)

This is supplemented by

ψψ

==0

(12.14)

for

m ≥ 0

. The number operator for the right-moving modes in the R sector is

Nndd

Rnnnn

=⋅+⋅

−−

∞

∑

()

αα

(12.15)

The operator

is given by

(12.16)

since the ordering constant is 0 for the R sector. Hence the mass-shell condition for

the R sector gives

′

(12.17)

212

String Theory Demystiﬁ ed

In Chap. 9, we learned that there is a simpler, uniﬁ ed description for superstrings

using the GS formalism. Since we are dealing with different physics for the left-

and right-moving modes, why not take this approach instead of carrying around the

NS and R sectors. Using the GS formalism, the number operator for the right-

moving modes is given by

NnSS

Rnnn

=⋅+

(

)

−−

∞

∑

αα

(12.18)

In the GS formalism, the mass-shell condition gives us an expression for the

mass that is similar to what we found for the R sector in the RNS formalism:

′

(12.19)

There will be two number operators for the left-moving modes. One for the P

sector, and one for the A sector. Given what we learned in Chap. 11, these can be

written down immediately for the case of the



nn n

=⋅+

(

)

=⋅+

−−

∞

−

∞

∑

αα λλ

αα

∑∑∑

−

∞

λλ

12/

(12.20)

The left-moving modes must also satisfy the Virasoro constraints. In general, the

mass-shell condition is

()



0−=

(12.21)

There is no supersymmetry for the left-moving modes, so the condition [Eq. (12.21)]

is only augmented by



= 0

(12.22)

for m > 0

. These constraints must be satisﬁ ed for the P and A sectors. So we

introduce two normal ordering constants which we denote by



and

. Then

Eq. (12.21) becomes the two conditions:

CHAPTER 12 Heterotic String Theory

213

()



−=

(P sector)

(A sector))

(12.23)

The



are not identical in these two equations, since we have the two number

operators [Eq. (12.20)]. So we have









=+−

(P sector)

(AA sector)

(12.24)

The task now is to determine the values of



and

. It turns out that this can be

done readily given what we know about superstrings. That is

• A periodic boson makes a contribution of 1/24 to the normal ordering

constant.

• A periodic fermion makes a contribution of −1/24 to the normal ordering

constant.

The normal ordering constant is actually formed by the sum



a = bosonic contribution + fermionic contriibution

Going to the light-cone gauge, there are eight transverse bosonic components.

We also have the 32 fermions

. So, the total normal ordering constant for the

P sector is



⎛

⎝

⎜

⎞

⎠

⎟

+−

⎛

⎝

⎜

⎞

⎠

⎟

=−8

(12.25)

Now for the A sector, we need to know that

• An antiperiodic fermion contributes 1/48 to the normal ordering constant.

In the A sector, the bosonic contribution is the same. Hence



⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

(12.26)

214

String Theory Demystiﬁ ed

You should be aware that the bosonic and fermionic contributions to the normal

ordering constants are due to the zero point energy of the bosonic and fermionic

modes. Note also that these zero energy contributions are ﬁ nite.

Using Eqs. (12.24), (12.25), and (12.26) and including the relation obtained for

the right-moving modes, we obtain the mass formulas for the P and A sectors:

′

== +

(

)

′

== −

mN N

88 1



(P sector)

(

)

(A sector)

(12.27)

We have made the obvious leap of faith that the mass must be the same for a

given string state whether looking at the right-moving or left-moving modes. We

immediately notice that

• A state with zero mass has

= 0

Put another way, a state with zero mass in heterotic string theory has the right-

moving modes in the ground state. In addition, if

m = 0

, then

• For a state in the P sector,



=−1

• For a state in the A sector,



=+1

Now, in ordinary quantum mechanics, you learned that a number operator

satisﬁ es

N ≥

. So, we must reject the ﬁ rst possibility which translates into

• The P sector contains no massless states.

The Spectrum

To describe the spectrum of the theory, we follow the usual procedure of constructing

states which are tensor products of left-moving and right-moving modes:

=⊗left right

(12.28)

For the left movers, we just learned that the P sector contributes nothing to a

massless state. Since



=+1

, this means that the state from the A sector is in the

ﬁ rst excited state. There are two possibilities. It can be a bosonic state:

left =

−



(12.29)

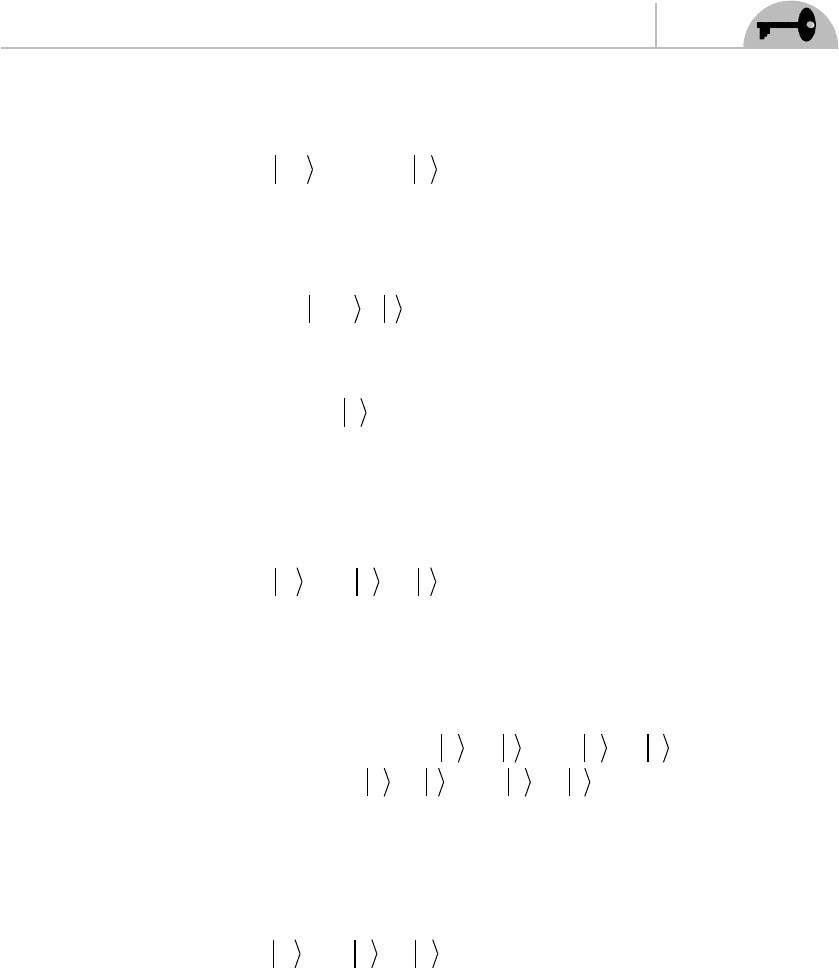
CHAPTER 12 Heterotic String Theory

215

Or it can be a fermionic state, since we need to consider the

as well:

left =

−−

λλ

12 12

(12.30)

For right movers, with

= 0

, we can have a bosonic state:

right = i

(12.31)

Or a fermionic state



(12.32)

Now let’s consider the case when the left movers are in the bosonic state

[Eq. (12.29)]. The bosonic sector is given by the tensor product with the

bosonic states of the right movers [Eq. (12.31)]:

ψα

=⊗

−



(12.33)

The states [Eq. (12.33)] can be summarized as follows. The “particle” spectrum

includes:

• A scalar, the dilaton

• An antisymmetric tensor state given by



αα

−−

⊗− ⊗

• The graviton which is the state



αα

−−

⊗+ ⊗

Now let’s take a look at the fermionic sector for the massless states. We can get

this by pairing up the bosonic states from the left movers with the fermionic states

from the right movers. This is going to give us the superpartners of Eq. (12.23). The

states can be written as

ψα

=⊗

−





(12.34)

The “particle” states here include

• The superpartner of the dilaton, the dilatino

• The superpartner of the graviton, the gravitino

As you might guess from looking at the particle spectrum, supersymmetry is a

vital component of string theory. If particle accelerators never ﬁ nd evidence of