Майсеня Л.И. Математика в примерах и задачах. Часть 2

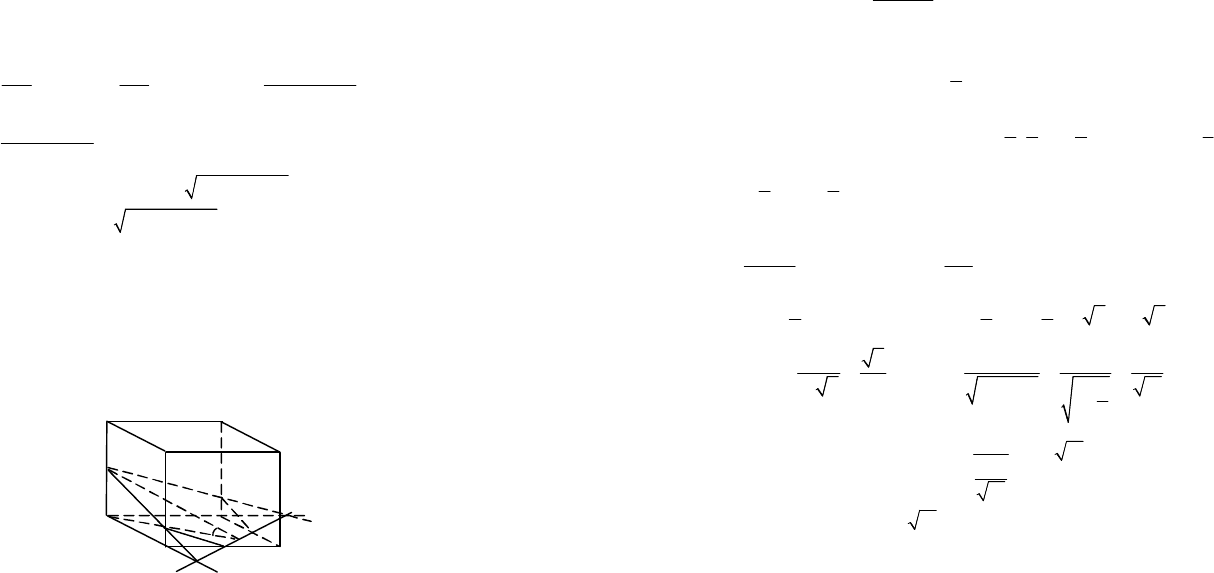
219 220

1

2

222

12

300,

875,

4,

4.

áîê

hd

add

Sah

×=

ì

ï

×=

ï

í

=+

ï

=

î

Из первых двух равенств выразим

22

12

dd

+

и подставим в третье.

Получим:

2

1

300

,

d

h

æö

=

ç÷

èø

2

875

,

d

h

æö

=

ç÷

èø

22

12

2

300875

,

dd

h

+

+=

22

2

300875

4a

h

+

= и далее

222222

43008752300875.

ahah=+Þ=+

Тогда

(

)

222

423008751850 ñì .

áîê

Sah==+=

Получаем ответ: 1850 см

2

.

Пример 5. На ребрах СС

1

, AD и АВ куба ABCDA

1

B

1

C

1

D

1

взяты со-

ответственно точки Р, М, R – середины этих ребер. Построить сечение

куба плоскостью, проходящей через точки Р, М, R. Считая ребро куба

равным 24 см, найти площадь полученного сечения.

Решение. Сделаем рисунок (рис. 12.14).

Рис. 12.14

Построение. Прямая MR – след секущей плоскости на плоскости

нижнего основания.

,

MRCBX

Ç=

1

.

PXBBN

Ç=

,

MRCDY

Ç=

1

.

PYDDK

Ç=

Получается искомое сечение куба PNRMK. Для вычис-

ления его площади воспользуемся теоремой о площади ортогональной

проекции многоугольника на плоскость. Рассмотрим многоугольник

PNRMK, его ортогональная проекция – СВRMD, определим, где угол

между плоскостями этих многоугольников. Ребром двугранного угла

является прямая MR. Из точки Р опустим перпендикуляр на прямую

MR:

,

PEMR

^

точка Е – середина отрезка MR.

.

CEMR

^

PEC

a

Ð=

– угол между плоскостью многоугольника и его проекцией. Теорему

запишем в виде

cos .

CBRMDPNRMK

SSPEC

=×Ð

Тогда

.

cos

CBRMD

PNRMK

S

a

=

Вычислим

.

CBRMD

S

Так как ABCD – квадрат, а треугольник

AMR

–

равнобедренный

1

,

2

ARAMAB

æö

==

ç÷

èø

то

( )

22

222

1111

1

2228

77

24504 ñì .

88

CBRMDABCDAMR

SSSABABABAB

AB

D

æö

=-=-××=-=

ç÷

èø

==×=

Вычислим

cos:

a

2

1

1tg;

cos

a

=+

tg

PC

CE

a

=

из

.

PCE

D

( )

1

12 ñì ,

2

PCCC==

()

33

242182 ñì ,

44

CEAC==×=

122

tg ,

3

182

a

==

2

113

cos.

211

1tg

1

9

a

===

+

Площадь сечения:

( )

2

504

16811 ñì .

3

11

PNRMK

S ==

Получаем ответ:

2

16811 ñì .

Задания

I уровень

1.1. Диагональ правильной четырехугольной призмы равна

25 см, а диагональ ее боковой грани – 20 см. Найдите высоту

призмы.

1.2. Сечение железнодорожной насыпи имеет вид трапеции,

нижнее основание которой 14 м, верхнее 8 м и высота 3,2 м. Оп-

ределите, сколько кубических метров земли приходится на 1 км

насыпи.

C

1

M

N

E

K

P

R

Y

a

D

1

B

1

А

1

D

С

В

А

221 222

1.3. В наклонной треугольной призме проведено сечение,

перпендикулярное боковому ребру, равному 12 см. В получен-

ном треугольнике две стороны с длинами

62

см и 8 см обра-

зуют угол 45°. Найдите площадь боковой поверхности призмы.

1.4. Основанием прямого параллелепипеда является ромб со

стороной 4 см и острым углом 60°. Найдите диагонали паралле-

лепипеда, если длина бокового ребра равна 10 см.

1.5. Основанием прямого параллелепипеда является квадрат

с диагональю, равной

82

см. Боковое ребро параллелепипеда

5 см. Найдите площадь полной поверхности параллелепипеда.

1.6. Основанием наклонного параллелепипеда является пря-

моугольник со сторонами 3 см и 4 см. Боковое ребро, равное

63

см, наклонено к плоскости основания под углом 60°. Най-

дите объем параллелепипеда.

1.7. Вычислите площадь поверхности прямоугольного па-

раллелепипеда, если два ребра и диагональ, исходящие из одной

вершины, равны соответственно 11 см,

23

см и 13 см.

1.8. Определите вес каменной колонны, имеющей форму

прямоугольного параллелепипеда, с размерами 0,3 м, 0,3 м и

2,5 м, если удельный вес материала равен 2,2 г/см

3

.

1.9. Найдите площадь диагонального сечения куба, если

диагональ его грани равна

132

дм.

1.10. Найдите объем куба, если расстояние между двумя его

вершинами, не лежащими в одной грани, равно

52

см.

II уровень

2.1. Основанием наклонной призмы является равносторон-

ний треугольник со стороной

43

см. Боковое ребро наклонено

к плоскости основания под углом 30°. Найдите площадь сечения

призмы, проходящего через боковое ребро и высоту призмы,

если известно, что одна из вершин верхнего основания проекти-

руется на середину стороны нижнего основания.

2.2. Основанием наклонной призмы является равносторон-

ний треугольник ABC со стороной, равной 3 см. Вершина A

1

проектируется в центр треугольника ABC. Ребро AA

1

составляет

с плоскостью основания угол 45°. Найдите площадь боковой по-

верхности призмы.

2.3. Вычислите объем наклонной треугольной призмы, если

стороны основания 7 см, 5 см и 8 см, а высота призмы равна

меньшей высоте треугольника-основания.

2.4. Диагональ правильной четырехугольной призмы накло-

нена к боковой грани под углом 30°. Найдите угол наклона к

плоскости основания.

2.5. Основанием прямой призмы является равнобедренная

трапеция, основания которой равны 4 см и 14 см, а диагональ –

15 см. Две боковые грани призмы – квадраты. Найдите площадь

полной поверхности призмы.

2.6. Диагонали правильной шестиугольной призмы равны

19 см и 21 см. Найдите ее объем.

2.7. Найдите измерения прямоугольного параллелепипеда, у

которого диагональ равна 8 дм, и она образует с боковыми гра-

нями углы 30° и 40°.

2.8. Диагонали основания прямого параллелепипеда равны

34 см и 38 см, а площади боковых граней – 800 см

2

и 1200 см

2

.

Найдите объем параллелепипеда.

2.9. Определите объем прямоугольного параллелепипеда, в

котором диагонали боковых граней, выходящие из одной вер-

шины, равны 4 см и 5 см и образуют угол 60°.

2.10. Найдите объем куба, если расстояние от его диагонали

до непересекающегося с ней ребра равно

32

мм.

223 224

III уровень

3.1. В правильной треугольной призме проведено сечение

через сторону основания и середину противоположного боково-

го ребра. Площадь основания равна 18 см

2

, а диагональ боковой

грани наклонена к основанию под углом 60°. Найдите площадь

сечения.

3.2. В основании призмы лежит квадрат ABCD, все вершины

которого равноудалены от вершины A

1

верхнего основания.

Угол между боковым ребром и плоскостью основания равен 60°.

Сторона основания – 12 см. Постройте сечение призмы плоско-

стью, проходящей через вершину C, перпендикулярно ребру

AA

1

, и найдите его площадь.

3.3. Основанием прямой призмы является равнобедренная

трапеция. Площадь диагонального сечения и площади парал-

лельных боковых граней соответственно равны 320 см

2

, 176 см

2

и 336 см

2

. Найдите площадь боковой поверхности призмы.

3.4. Площадь основания прямой треугольной призмы равна

9 см

2

, площади боковых граней 18 см

2

, 20 см

2

и 34 см

2

. Найдите

объем призмы.

3.5. Найдите диагонали прямоугольного параллелепипеда,

зная, что диагонали его граней равны 11 см, 19 см и 20 см.

3.6. Углы, образованные диагональю основания прямо-

угольного параллелепипеда со стороной основания и диагона-

лью параллелепипеда, равны соответственно

a

и

b

. Найдите

площадь боковой поверхности параллелепипеда, если его диаго-

наль равна d.

3.7. Площадь того сечения куба, которое представляет собой

правильный шестиугольник, равна

273

см

2

. Найдите площадь

поверхности куба.

3.8. Измерения одного прямоугольного параллелепипеда от-

носятся как 3 : 5 : 6, а измерения второго – как 3 : 6 : 7. Зная, что

их площади полных поверхностей относятся как 7 : 9, найдите

отношения объемов.

3.9. Основанием наклонного параллелепипеда является ромб

со стороной, равной b, и углом 60°. Боковое ребро также равно b

и образует с прилежащими сторонами основания углы по 45°.

Найдите объем параллелепипеда.

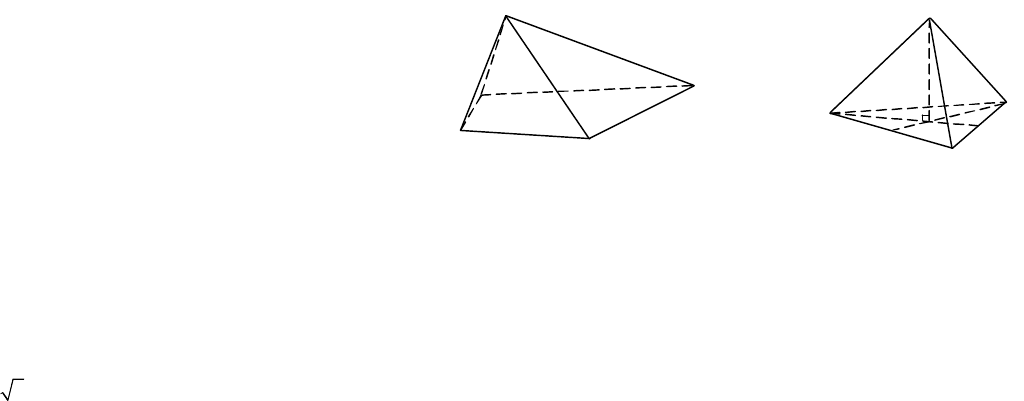
12.3. Пирамида. Усеченная пирамида

Пирамидой называется многогранник, одна из граней кото-

рого – многоугольник (основание), а все остальные грани – тре-

угольники с общей вершиной (боковые грани) (рис. 12.15). Пи-

рамида называется правильной, если ее основанием является

правильный многоугольник и вершина пирамиды проектируется

в центр основания (рис. 12.16). Треугольная пирамида, у которой

все ребра равны, называется тетраэдром.

Рис. 12.15 Рис. 12.16

Боковым ребром пирамиды называется сторона боковой

грани, не принадлежащая основанию. Высотой пирамиды назы-

вается расстояние от ее вершины до плоскости основания. Все

боковые ребра правильной пирамиды равны между собой, все

боковые грани – равные равнобедренные треугольники. Высота

боковой грани правильной пирамиды, проведенная из вершины,

называется апофемой. Диагональным сечением называется се-

чение пирамиды плоскостью, проходящей через два боковых

ребра, не принадлежащих одной грани.

Площадью боковой поверхности пирамиды называется

сумма площадей всех боковых граней. Площадью полной по-

верхности называется сумма площадей всех боковых граней и

основания.

S

D

С

В

А

A

C

B

S

O

225 226

Теоремы:

1. Если в пирамиде все боковые ребра равнонаклонены к

плоскости основания, то вершина пирамиды проектируется в

центр окружности, описанной около основания.

2. Если в пирамиде все боковые ребра имеют равные длины,

то вершина пирамиды проектируется в центр окружности, опи-

санной около основания.

3. Если в пирамиде все грани равнонаклонены к плоскости

основания, то вершина пирамиды проектируется в центр окруж-

ности, вписанной в основание.

Для вычисления объема произвольной пирамиды верна

формула:

1

,

3

îñí

VSÍ

=×

где V – объем; S

осн

– площадь основания; H – высота пира-

миды.

Для правильной пирамиды верны формулы:

1

,

2

áîê a

Sph

=

,

ïîëíáîêîñí

SSS=+

1

,

3

îñí

VSÍ

=×

где S

бок

– площадь боковой поверхности; p – периметр осно-

вания; h

а

– апофема; S

полн

– площадь полной поверхности; S

осн

–

площадь основания; V – объем правильной пирамиды; H – высота.

Усеченной пирамидой называется часть пирамиды, заклю-

ченная между основанием и секущей плоскостью, параллельной

основанию пирамиды (рис. 12.17). Правильной усеченной пи-

рамидой называется часть правильной пирамиды, заключенная

между основанием и секущей плоскостью, параллельной осно-

ванию пирамиды.

Основания усеченной пирамиды – подобные многоугольни-

ки. Боковые грани – трапеции. Высотой усеченной пирамиды

называется расстояние между ее основаниями. Диагональю усе-

ченной пирамиды называется отрезок, соединяющий ее верши-

ны, не лежащие в одной грани. Диагональным сечением назы-

вается сечение усеченной пирамиды плоскостью, проходящей

через два боковых ребра, не принадлежащих одной грани.

Рис. 12.17

Для усеченной пирамиды справедливы формулы:

( )

12

1212

,

1

,

3

ïîëíáîê

SSSS

V Í SSSS

=++

(12.4)

где S

полн

– площадь полной поверхности; S

бок

– площадь бо-

ковой поверхности; S

1

, S

2

– площади верхнего и нижнего осно-

ваний; V – объем усеченной пирамиды; H – высота.

Для правильной усеченной пирамиды верна формула:

( )

12

1

,

2

áîê a

Spph

=+

где p

1

, p

2

– периметры оснований; h

а

– апофема правильной

усеченной пирамиды.

Пример 1. В правильной треугольной пирамиде двугранный угол

при основании равен 60º. Найти тангенс угла наклона бокового ребра к

плоскости основания.

Решение. Сделаем рисунок (рис. 12.18).

Рис. 12.18

C

1

B

1

A

1

C

B

A

j

a

D

A

C

B

S

O

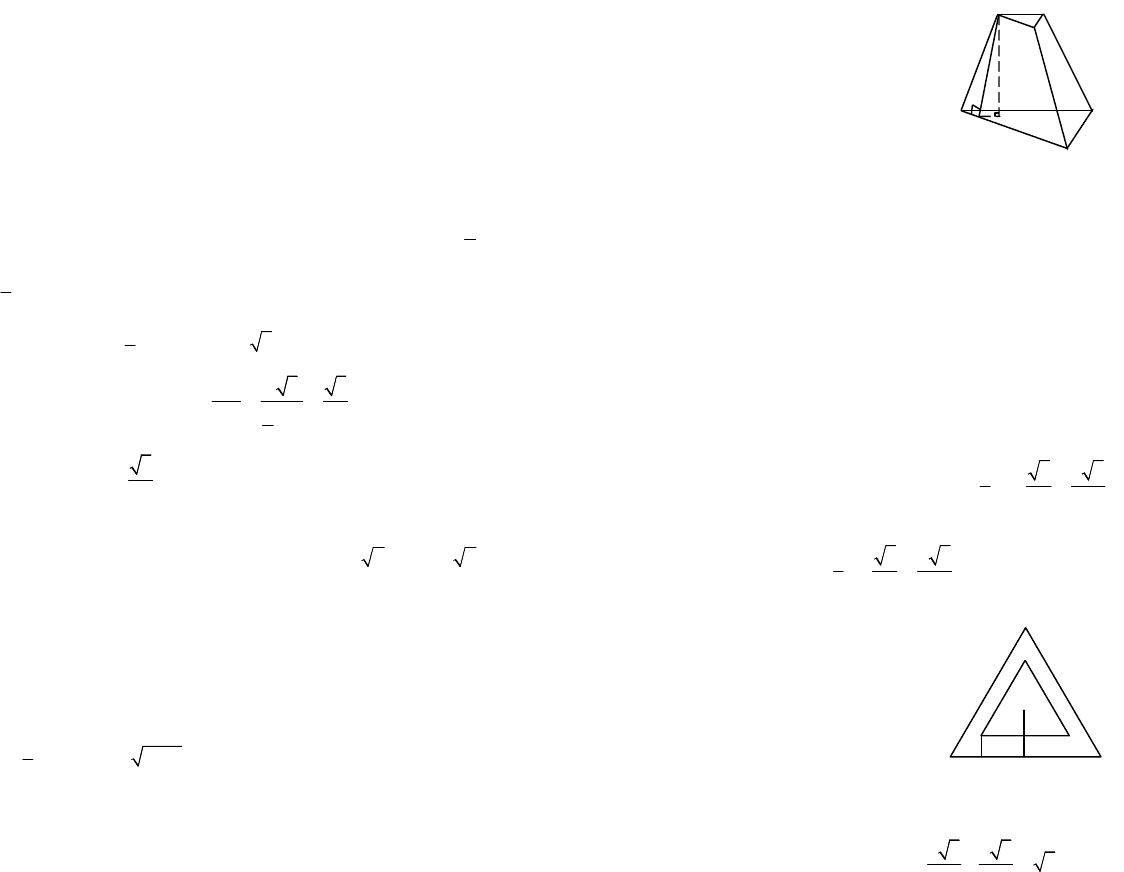
227 228

Пирамида правильная, значит в основании лежит равносторон-

ний треугольник и все боковые грани – равные равнобедренные тре-

угольники. Двугранный угол при основании – это угол наклона боко-

вой грани пирамиды к плоскости основания. Линейным углом будет

угол

a

между двумя перпендикулярами:

BDAC

^

и

,

SDAC

^

т. е.

60.

SDB

a

=Ð=°

Вершина пирамиды проектируется в центре тре-

угольника (центр описанной окружности и вписанной окружности в

треугольник АВС). Угол наклона бокового ребра (например SB) – это

угол между самим ребром и его проекцией на плоскость основания.

Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс

,

SBO

j

Ð=

необходимо знать катеты SO и OB. Пусть длина отрезка

BD равна 3а. Точкой О отрезок BD делится на части:

2

3

BOBD

=

и

1

.

3

DOBD

=

Из

SOD

D

находим SO:

1

tg 3tg 603.

3

SODOaa

a

=×=××°=

Из

SBO

D

находим:

33

tg .

2

3

SOa

BO

a

j

===

×

Получаем ответ:

3

.

2

Пример 2. Найти объем правильной усеченной четырехугольной

пирамиды, если диагонали ее оснований равны

22

см и

82

см, а

высота – 4 см.

Решение. Для нахождения объема усеченной пирамиды восполь-

зуемся формулой (12.4). Чтобы найти площади оснований, необходимо

найти стороны квадратов-оснований, зная их диагонали. Стороны ос-

нований равны соответственно 2 см и 8 см. Значит, площади оснований

равны

2

1

4 ñì

S = и

2

64 ñì .

S = Подставив все данные в формулу,

вычислим объем усеченной пирамиды:

( ) ( )

3

1

4464464112 cì .

3

V =××++×=

Получаем ответ: 112 см

3

.

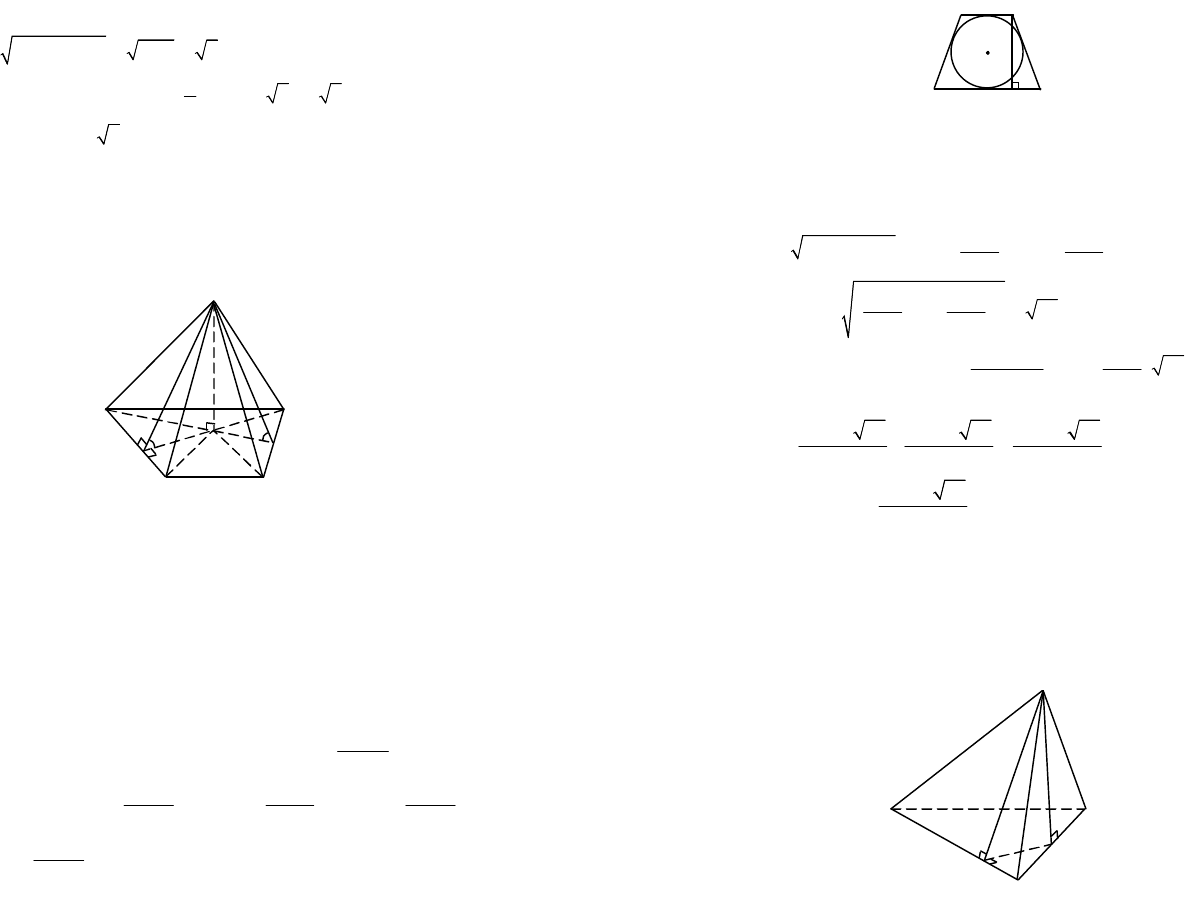
Пример 3. Найти площадь боковой грани правильной треугольной

усеченной пирамиды, стороны оснований которой равны 10 см и 4 см,

а высота пирамиды – 2 см.

Решение. Сделаем рисунок (рис. 12.19).

Рис. 12.19

Боковой гранью данной пирамиды является равнобокая трапеция.

Для вычисления площади трапеции необходимо знать основания и вы-

соту. Основания даны по условию, остается неизвестной только высо-

та. Ее найдем из

1

,

AED

D где А

1

Е – перпендикуляр из точки А

1

на

плоскость нижнего основания, A

1

D – перпендикуляр из точки А

1

на АС.

А

1

Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем

дополнительно рисунок, на котором изобразим вид сверху (рис. 12.20).

Точка О – проекция центров верхнего и нижнего оснований.

11

,

ÎÌÀÑ

^

,

ÎÊÀÑ

^

1

,

ADMK

= так как

1

ADED

= (рис. 12.20) и

,

EDAC

^

.

MKAC

^

С другой стороны, ОК – радиус вписанной в

ABC

D

окружности и

( )

1353

10 ñì .

323

OK =××= ОМ – радиус впи-

санной в

111

ABC

D окружности:

( )

1323

4 ñì .

323

OÌ=××=

Рис. 12.20

( )

5323

3 ñì .

33

ÌÊÎÊÎÌ=-=-= MK = DE.

E

D

C

1

B

1

A

1

C

B

A

D

К

С

В

А

М

О

Е

А

1

B

1

C

1

229 230

По теореме Пифагора из

1

:

ADE

D

( )

22

11

437ñì .

ADAEDE=+=+=

Площадь боковой грани:

( )

2

1

104777 ñì .

2

S =+×=

Получаем ответ:

2

77 ñì .

Пример 4. В основании пирамиды лежит равнобокая трапеция,

основания которой а и b (a > b). Каждая боковая грань образует с плос-

костью основания пирамиды угол, равный

j

. Найти площадь полной

поверхности пирамиды.

Решение. Сделаем рисунок (рис. 12.21).

Рис. 12.21

Площадь полной поверхности пирамиды SABCD равна сумме

площадей

,

SAB

D

,

SAD

D

,

SBC

D

SDC

D

и площади трапеции ABCD.

Воспользуемся утверждением, что если все грани пирамиды рав-

нонаклонены к плоскости основания, то вершина проектируется в

центр вписанной в основание окружности. Точка О – проекция верши-

ны S на основание пирамиды. Треугольник SOD является ортогональ-

ной проекцией треугольника CSD на плоскость основания. По теореме

о площади ортогональной проекции плоской фигуры имеем:

cos,

CODCSD

SS

j

DD

=×

откуда получаем:

.

cos

COD

CSD

S

j

D

=

Аналогично

,

cos

OAD

SAD

S

j

D

=

,

cos

OBA

SBD

S

j

D

=

cos

OBC

SBC

S

j

D

= и,

значит,

.

cos

ABCD

ïîëí ABCD

S

SS

j

=+ Таким образом, задача свелась к нахож-

дению площади трапеции АВСD. Изобразим трапецию ABCD отдельно

(рис. 12.22). Точка О – центр вписанной в трапецию окружности.

Рис. 12.22

Так как в трапецию можно вписать окружность, то

ÀDBCABDC

+=+

или

2.

abDC

+= Из

DCH

D

по теореме Пифаго-

ра имеем:

22

,

DHDCHC

=-

,

2

ab

DC

+

=

.

2

ab

HC

-

=

Тогда

22

.

22

abab

DHab

+-

æöæö

=-=

ç÷ç÷

èøèø

Площадь трапеции:

.

22

ABCD

ADBCab

SDHab

++

=×=×

Следовательно,

( ) ( ) ( )

( )

1cos.

2cos22cos

ïîëí

abababababab

S

j

jj

+++

=+=+

Получаем ответ:

( )

1cos.

2cos

abab

j

+

Пример 5. Основание пирамиды – равносторонний треугольник

со стороной а. Одна из боковых граней – равнобедренный прямоуголь-

ный треугольник, плоскость которого перпендикулярна плоскости ос-

нования. Найти площадь боковой поверхности пирамиды.

Решение. Сделаем рисунок (рис. 12.23).

Рис. 12.23

О

S

D

С

В

А

j

B

H

C

D

А

О

A

E

C

D

B

S

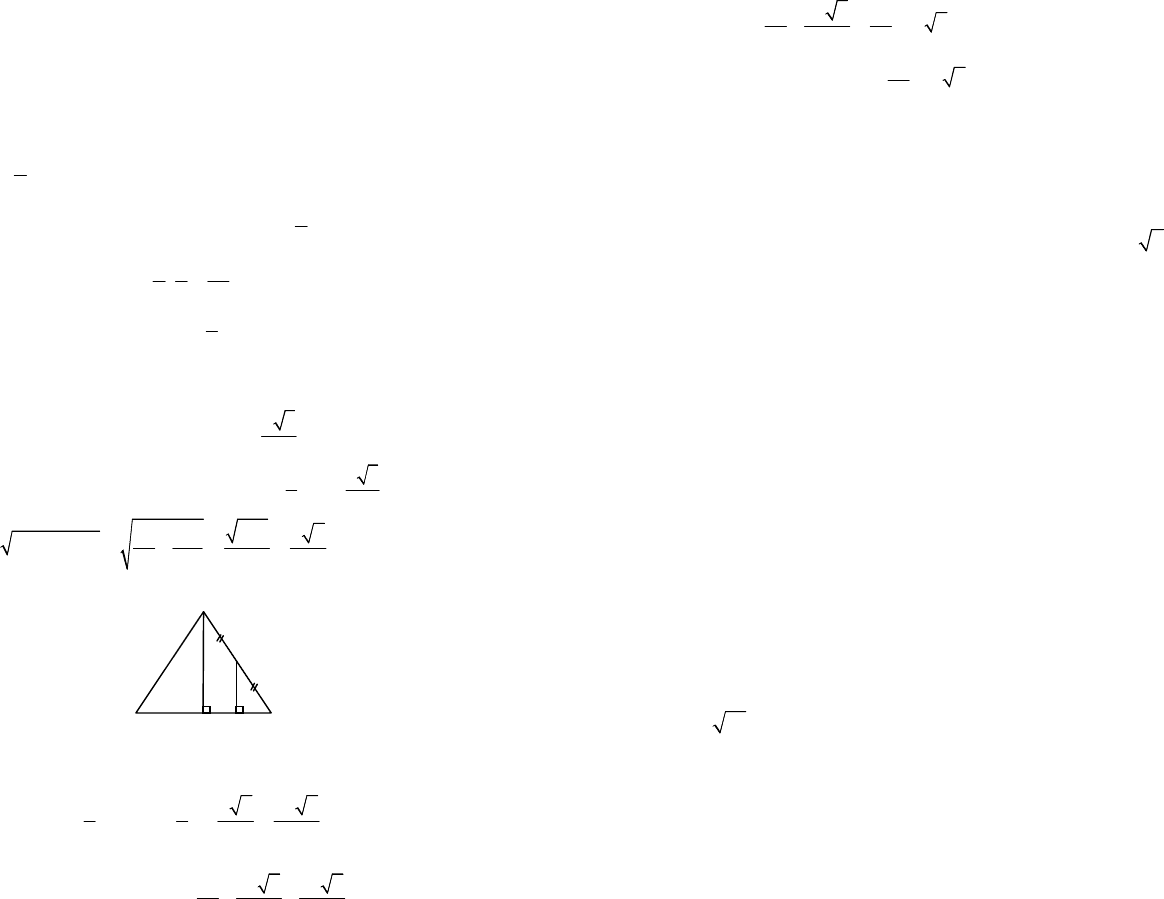
231 232

Площадь боковой поверхности данной пирамиды SABC состоит из

суммы площадей ее боковых граней. Боковые грани – треугольники,

один из которых прямоугольный и равнобедренный (

,

SCB

D

90

S

Ð=°

), два других – равные треугольники

(

)

.

SACSAB

D=D Рас-

смотрим

,

SCB

D

90,

S

Ð=°

,

BCa

=

SCSB

=

– по условию. Вычис-

лим его площадь:

.

SBC

SSDDB

D

=×

Так как

SCB

D

равнобедренный, то

,

2

a

DCDB== а так как

90,

S

Ð=°

то

45

CB

Ð=Ð=°

и, следова-

тельно, в

SDB

D

45,

SB

Ð=Ð=°

.

2

a

SDDB

==

Тогда

2

.

224

SBC

aaa

SSDDB

D

=×=×=

Рассмотрим

.

SAC

D

1

.

2

SAC

SACSE

D

=×

SE найдем из

,

SDE

D

90.

D

Ð=°

По теореме Пифагора имеем

222

.

SESDDE

=+ Найдем

DE. Для этого рассмотрим равносторонний треугольник основания

(рис. 12.24).

,

BHAC

^

.

AHCH

=

3

.

2

a

BH = В

BHC

D

отрезок DE

является средней линией, следовательно,

13

.

24

a

DEBH==

Находим SE:

222

22

377

.

416164

aaaa

SESDDE=+=+==

Рис. 12.24

Теперь

2

1177

.

2248

SAC

aa

SACSEa

D

=×=××=

Площадь боковой поверхности пирамиды равна:

222

77

488

áîê SBCSACSAB

aaa

SSSS

DDD

=++=++=

( )

222

7

17.

444

aaa

=+=+

Получаем ответ:

( )

2

17.

4

a

+

Задания

I уровень

1.1. Боковое ребро правильной четырехугольной пирамиды

равно диагонали основания, длина которой

32

см. Найдите

высоту пирамиды и сторону ее основания.

1.2. Основанием пирамиды является треугольник со сторо-

нами 6 см, 8 см и 10 см. Боковые грани наклонены к плоскости

основания под углом 60º. Найдите высоту пирамиды.

1.3. Найдите площадь полной поверхности правильной шес-

тиугольной пирамиды, зная, что апофема равна 10 см, а радиус

окружности, описанной около основания, равен 6 см.

1.4. Найдите высоту правильной четырехугольной пирами-

ды, сторона которой 6 см, если ее объем равен объему куба со

стороной 4 см.

1.5. Боковые ребра треугольной пирамиды взаимно перпен-

дикулярны и равны b. Найдите объем пирамиды.

1.6. Стороны оснований правильной усеченной четырех-

угольной пирамиды равны 8 см и 4 см. Боковое ребро равно

17

см. Найдите высоту пирамиды.

1.7. Боковые ребра правильной усеченной шестиугольной

пирамиды наклонены к плоскости нижнего основания под углом

45º. Стороны оснований равны 10 см и 5 см. Найдите длину бо-

кового ребра и высоту пирамиды.

1.8. Боковая грань правильной семиугольной усеченной пи-

рамиды – равнобедренная трапеция, средняя линия которой рав-

A

H

E

C

D

B

233 234

на 13 см, а высота – 8 см. Вычислите площадь боковой поверх-

ности пирамиды.

1.9. Площадь полной поверхности правильной треугольной

усеченной пирамиды равна

34348

+

см

2

. Стороны оснований –

10 см и 6 см. Найдите тангенс угла между боковым ребром и

стороной нижнего основания.

1.10. В правильной усеченной четырехугольной пирамиде

стороны оснований равны 5 см и 17 см, боковые грани наклоне-

ны к плоскости основания под углом 45º. Вычислите объем пи-

рамиды.

II уровень

2.1. По стороне основания, равной 5 см, и высоте, равной

12 см, найдите апофему и боковое ребро правильной шести-

угольной пирамиды.

2.2. Найдите расстояние между центрами окружностей, впи-

санных в смежные боковые грани тетраэдра. Радиус окружности

равен

23

дм.

2.3. Основание пирамиды – ромб со стороной 6 см и углом

45º, все двугранные углы при сторонах основания пирамиды

равны 30º. Вычислите площадь полной поверхности пирамиды.

2.4. В правильной треугольной пирамиде боковое ребро рав-

но 8 см, а плоский угол при вершине – 30º. Найдите площадь

полной поверхности пирамиды.

2.5. Одно из самых грандиозных сооружений древности –

пирамида Хеопса – имеет форму правильной четырехугольной

пирамиды высотой » 150 м и боковым ребром » 220 м. Найдите

объем этой пирамиды.

2.6. Определите объем правильной треугольной пирамиды,

если боковая грань наклонена к плоскости основания под углом

60º и удалена от противоположной вершины на расстояние, рав-

ное 3 см.

2.7. В правильной четырехугольной усеченной пирамиде

стороны оснований равны 15 дм и 5 дм. Площадь диагонального

сечения равна

1202

дм

2

. Найдите площадь полной поверхно-

сти пирамиды.

2.8. Основания усеченной пирамиды – равнобедренные тре-

угольники, их равные стороны – 8 см и 4 см, углы при вершинах

треугольников равны по 120º. Ребро, проходящее через вершины

данных углов, перпендикулярно плоскости оснований и равно

3 см. Вычислите площадь боковой поверхности пирамиды.

2.9. Правильная четырехугольная пирамида, сторона осно-

вания которой 1500 см и высота 2000 см, пересечена плоско-

стью, параллельной основанию. Найдите объем усеченной пи-

рамиды, если ее высота равна 1400 см.

2.10. В правильной усеченной треугольной пирамиде сторо-

ны оснований равны 7 см и 3 см, а апофема – 5 см. Найдите объ-

ем пирамиды.

III уровень

3.1. Основанием пирамиды является равносторонний тре-

угольник. Одна из боковых граней пирамиды перпендикулярна

плоскости основания, две другие образуют с плоскостью осно-

вания угол

a

. Найдите косинус угла между этими гранями.

3.2. Все диагональные сечения правильной шестиугольной

пирамиды SABCDEF равновелики. Найдите угол между плоско-

стью основания и плоскостью сечения SAC.

3.3. Точка М – середина ребра SB пирамиды SABC, основа-

нием которой является правильный треугольник ABC, а боковое

ребро SC перпендикулярно плоскости ABC и SC = 2AB. Найдите

расстояние от точки М до прямой AC, если АВ = а.

3.4. Основанием пирамиды служит ромб со стороной а и

острым углом

a

. Две боковые грани перпендикулярны основа-

нию, а две другие наклонены к нему под углом

j

. Найдите пло-

щадь боковой поверхности пирамиды.

235 236

3.5. Основанием пирамиды является равнобокая трапеция,

острый угол которой

a

, а площадь Q. Каждая боковая грань об-

разует с основанием угол

b

. Найдите объем пирамиды.

3.6. Основание усеченной пирамиды – прямоугольник со

сторонами 6 см и 8 см. Одно из боковых ребер перпендикулярно

плоскости основания и равно 7 см. Вершина верхнего основания

проектируется в точку пересечения диагоналей нижнего основа-

ния. Найдите длины остальных боковых ребер и угол наклона

большего бокового ребра к плоскости основания.

3.7. Основания усеченной пирамиды – квадраты со сторона-

ми 8 см и 4 см. Одна из боковых граней перпендикулярна плос-

кости основания и является равнобедренной трапецией. Проти-

волежащая ей грань образует с плоскостью основания угол 60º.

Найдите площади боковых граней пирамиды.

3.8. Стороны оснований и высота правильной четырех-

угольной усеченной пирамиды относятся как 7 : 4 : 2, площадь

боковой поверхности равна 110 дм

2

. Вычислите площадь полной

поверхности пирамиды.

3.9. Найдите объем правильной треугольной усеченной пи-

рамиды, у которой стороны оснований равны 3 м и 2 м, а пло-

щадь боковой поверхности равна сумме площадей оснований.

3.10. Стороны оснований правильной четырехугольной усе-

ченной пирамиды равны 2 см и 1 см, высота – 3 см. Через точку

пересечения диагоналей пирамиды, параллельно основаниям

пирамиды, проведена плоскость, делящая пирамиду на две час-

ти. Найдите объем каждой из полученных частей.

12.4. Цилиндр

Цилиндрической поверхностью называется поверхность,

образованная всеми прямыми, проходящими через каждую точ-

ку данной кривой параллельно данной прямой (рис. 12.25).

Данная кривая называется направляющей, а прямые – обра-

зующими цилиндрической поверхности.

Прямой круговой цилиндрической поверхностью называ-

ется поверхность, образованная всеми прямыми, проходящими

через каждую точку данной окружности перпендикулярно плос-

кости этой окружности. В дальнейшем эту поверхность будем

кратко называть цилиндрической (рис. 12.26).

Цилиндром (прямым круговым цилиндром) называется

геометрическое тело, ограниченное цилиндрической поверхно-

стью и двумя параллельными плоскостями, которые перпенди-

кулярны образующим поверхности (рис. 12.27).

Рис. 12.25 Рис. 12.26 Рис. 12.27

Цилиндр можно рассматривать как тело, полученное при

вращении прямоугольника вокруг оси, содержащей одну из сто-

рон прямоугольника.

Два круга, ограничивающие цилиндр, называются его осно-

ваниями. Прямая, проходящая через центры данных кругов, на-

зывается осью цилиндра. Отрезки, образующие цилиндрическую

поверхность, называются образующими цилиндра. Высотой

цилиндра называется расстояние между его основаниями. Осе-

вым сечением называется сечение, проходящее через ось ци-

линдра. Разверткой боковой поверхности цилиндра называется

прямоугольник со сторонами, равными длине окружности осно-

вания и длине образующей цилиндра.

Для цилиндра верны формулы:

2

,

îñí

SR

p

=

2,

áîê

SRH

p

=

2

2,

ïîëí

SRHR

pp

=+ (12.5)

2

,

VRH

p

= (12.6)

где S

осн

– площадь основания; R – радиус основания; S

бок

–

площадь боковой поверхности; H – высота; S

полн

– площадь пол-

l

а

a

b

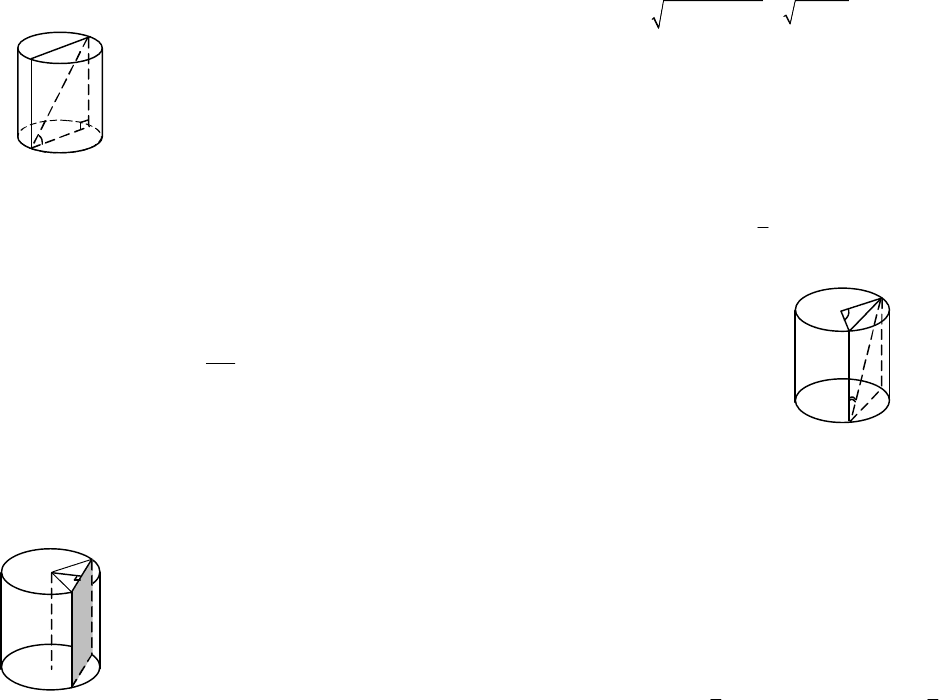
237 238

ной поверхности; V – объем цилиндра.

Пример 1. Найти радиус основания цилиндра, если его высота

равна 8 см, а диагональ осевого сечения составляет угол 45º с плоско-

стью основания.

Решение. Сделаем рисунок (рис. 12.28).

Рис. 12.28

Осевое сечение цилиндра – это прямоугольник, одна сторона ко-

торого – образующая (высота) цилиндра, вторая сторона – диаметр

основания цилиндра. Рассмотрим треугольник АВС, у которого катета-

ми являются диаметр основания АС и высота ВС, а гипотенузой – диа-

гональ сечения АВ. Так как

45,

ÂÀÑ

Ð=°

то

ÀÂÑ

D

– равнобедрен-

ный и АС = ВС = 8 см. АС – диаметр, значит, радиус

4 ñì .

2

ÀÑ

=

Получаем ответ: 4 см.

Пример 2. Цилиндр пересечен плоскостью, параллельной оси.

Найти площадь сечения, если радиус основания и высота цилиндра

соответственно равны 5 см и 10 см, а расстояние от оси цилиндра до

плоскости сечения – 3 см.

Решение. Сделаем рисунок (рис. 12.29).

Рис. 12.29

Сечением цилиндра является прямоугольник, одна из сторон ко-

торого – хорда окружности основания (ВС), вторая – образующая ци-

линдра (ВА). Образующая равна высоте, значит ВА = 10 см. Необходи-

мо найти хорду ВС. Расстояние от оси ОО

1

до плоскости сечения – это

перпендикуляр, опущенный из точки О

1

на хорду ВС. Проведя радиусы

О

1

С и О

1

В, получим равнобедренный треугольник

1

.

ÎÂÑ

Высота O

1

D

является его медианой, значит BD = DC. Из

1

Î DÂ

D найдем BD:

( )

2222

11

534 ñì .

BDOBOD=-=-=

Тогда BC = 2BD = 8 см. Площадь сечения:

(

)

2

10880 ñì .

ABCD

SABBC=×=×=

Получаем ответ: 80 см

2

.

Пример 3. Диагональ сечения цилиндра, параллельного его оси,

равна d и образует угол

a

с образующей цилиндра. Найти площадь

полной поверхности цилиндра, если секущая плоскость отсекает от

окружности основания

1

3

часть.

Решение. Сделаем рисунок (рис. 12.30).

Рис. 12.30

Площадь полной поверхности цилиндра вычисляется по форму-

ле (12.5).

Чтобы найти высоту Н (образующую), рассмотрим

.

ABD

D

В нем

90,

A

Ð=°

,

B

a

Ð=

.

BDd

=

Тогда

coscos;

ABBDd

aa

=×=×

sinsin.

ADBDd

aa

=×=×

Для нахождения радиуса рассмотрим равнобедренный

,

AOD

D

в

котором OA = OD = R. Так как по условию сечение отсекает от окруж-

ности основания

1

3

часть, значит

1

360120.

3

AOD

Ð=×°=°

По теореме

косинусов найдем радиус:

222

2cos120,

ADAODOAOOD

=+-××°

т. е.

2222

sin22cos120.

dRR

a

=-°

В

А

О

С

D

C

B

D

А

О

1

О

C

B

D

А

О

a

Майсеня Л.И. Математика в примерах и задачах. Часть 2

Подождите немного. Документ загружается.