Майсеня Л.И. Математика в примерах и задачах. Часть 2

179 180

11. ПРОИЗВОДНАЯ ФУНКЦИИ

11.1. Понятие производной. Правила

дифференцирования. Таблица производных

Пусть функция

(

)

fx

определена в точке

0

x

и в некоторой ее

окрестности, x – точка из рассматриваемой окрестности. Прира-

щением аргумента в точке

0

x

называется величина

0

,

xxx

D=-

приращением функции – величина

00

()()().

fxfxfx

D=-

Если

выразить

0

,

xxx

=+D

то

000

()()().

fxfxxfx

D=+D-

Производной функции

(

)

fx

в точке

0

x

называется предел

отношения приращения функции к приращению аргумента, ко-

гда последнее стремится к нулю, при условии, что предел суще-

ствует.

Производную в точке обозначают

(

)

0

.

fx

¢

По определению

( )

(

)

(

)

(

)

00

000

0

limlim,

xx

fxfxxfx

fx

xx

D®D®

D+D-

¢

==

DD

(11.1)

или, что то же,

( )

(

)

(

)

0

lim,

xx

fxfx

fx

xx

®

-

¢

=

-

(11.2)

при условии, что пределы (11.1) и (11.2) существуют.

Функция, имеющая производную в точке, называется диф-

ференцируемой в этой точке. Операция нахождения производ-

ной называется дифференцированием.

Производная функции в точке – это число. Если функция

дифференцируема на некотором множестве X из ее области оп-

ределения, то

(

)

fx

¢

также является функцией (ее обозначают

также

y

¢

).

Основные правила дифференцирования

Пусть

(

)

,

UUx

=

(

)

VVx

= – дифференцируемые функции.

Справедливы формулы:

0,

C

¢

=

где

;

Cconst

=

(11.3)

( )

,

CUCU

¢

= где

;

Cconst

=

(11.4)

( )

;

UVUV

¢

¢¢

±=± (11.5)

( )

;

UVUVUV

¢

¢¢

=+ (11.6)

2

.

UUVUV

V

¢

¢¢

-

æö

=

ç÷

èø

(11.7)

Таблица производных основных элементарных функций

( )

1

,

xx

aa

a

-

¢

= где

,

a

Î

R

в частности:

( )

1

,

2

x

¢

=

2

11

;

x

¢

æö

=-

ç÷

èø

( )

ln,

xx

aaa

¢

= где

0,

a

>

1,

a

¹

в частности,

(

)

;

xx

ee

=

( )

1

log,

ln

a

x

xa

¢

= где

0,0,

xa

>>

1,

a

¹

в частности

( )

1

ln;

x

¢

=

( )

sincos;

xx

¢

=

( )

cossin;

xx

¢

=-

( )

2

1

tg;

cos

x

¢

=

( )

2

1

ctg;

sin

x

¢

=-

( )

2

1

arcsin;

1

x

¢

=

-

( )

2

1

arccos;

1

x

¢

=-

-

( )

2

1

arctg;

1

x

¢

=

+

181 182

( )

2

1

arcctg;

1

x

¢

=-

+

( )

shch;

xx

¢

=

( )

chsh;

xx

¢

=

( )

2

1

th;

ch

x

¢

=

( )

2

1

cth.

sh

x

¢

=-

Пример 1. Найти производную функции

(

)

yx

в точке

0

,

x

поль-

зуясь определением, если:

1)

(

)

2

234,

yxxx

=++

0

2;

x

=

2)

0

()sin,.

4

yxxx

p

==

Решение. 1) Используем определение производной в виде форму-

лы (11.1):

00

0

22

0000

0

222

00000

0

2

0

00

()()

()lim

2()3()4234

lim

242334234

lim

423

limlim(423)43.

x

xx

fxxfx

yx

x

xxxxxx

x

xxxxxxxx

x

xxxx

xxx

x

D®

D®®

+D-

¢

==

D

+D-+D+---

==

D

+D+D--D+---

==

D

D+D-D

==+D-=-

D

Поскольку по условию

0

2,

x

=

то

(

)

24235.

y

¢

=×-=

2) По формуле (11.1) получаем:

0000

0

00

()()sin()sin

()limlim.

xx

fxxfxxxx

yx

xx

D®D®

+D-+D-

¢

==

DD

Далее, применив тригонометрическую формулу

sin()sincoscossin,

ababab

+=-

получим:

0000

00

sincoscossinsinsincos

limlim

cossinsin

limlim.

xx

xxxxxxx

xx

xxx

xx

D®D®

D-D-D

=-

DD

D

--

DD

Так как при

0

x

D®

имеем

coscos01

x

D==

и, применив формулу

первого замечательного предела, получаем:

00

000

0000

sinsin

limlimcoslimlimcoscos.

xxxx

xx

xxx

xx

D®D®D®D®

--==

DD

Поскольку по условию

0

,

4

x

p

= то

2

cos.

442

y

pp

æö

¢

==

ç÷

èø

Пример 2. Вычислить производную функции

4

2,,

yxx=Î

R

пользуясь определением производной.

Решение. Пусть x – произвольная фиксированная точка из

().

Dy

=

R

Пользуясь формулой (11.1), имеем:

( ) () ( )

( ) ( ) ( ) ( )

( ) ( ) ( )

( ) ( )

( )

4

000

4234

44324

00

234

32

0

23

3233

0

22

limlimlim

464

2lim2lim

464

2lim

2lim464248.

xxx

xx

x

fxxfxxxx

y

xxx

xxxxxxxxxxxx

xx

xxxxxxx

x

xxxxxxxx

D®D®D®

D®D®

D®

+D-+D-

D

¢

====

DDD

+D-+D+D+D+D-

===

DD

D+D+D+D

==

D

=+D+D+D=×=

Таким образом, операция дифференцирования ставит в соответст-

вие функции

4

2,

yx

=

,

x

Î

R

функцию

3

8,.

yxx

¢

=Î

R

Пример 3. Найти производную функции:

1)

2

log

4cosarctg;

3

x

yxx

=+- 2)

2tg5;

yxx

=+

3)

3

5

.

1

x

y

x

=

-

Решение. 1) Дифференцируем функцию и используем формулы

(11.4), (11.5) и таблицу производных, получаем:

( ) ( )

( ) ( ) ( )

22

2

loglog

4cosarctg4cosarctg

33

111

4coslogarctg4sin.

33ln2

1

xx

yxxxx

xxxx

x

¢¢

æöæö

¢¢

¢

=+-=+-=

ç÷ç÷

èøèø

¢¢¢

=+-=-+-

+

2) Дифференцируем функцию по формулам (11.3)–(11.6) и соот-

ветствующим формулам таблицы производных:

( ) ( ) ( )

( )

22

2tg52tg02tgtg

11tg2

2tg.

2coscos

yxxxxxxxx

xx

xxxx

¢¢¢

æö

¢

¢¢

=+=+=×+×=

ç÷

èø

æö

=+=+

ç÷

èø

183 184

3) Дифференцируем функцию по формулам (11.7), (11.5), (11.3)

и первой формуле таблицы производных:

( ) ( ) ( )

( )

( ) ( )

( )

( ) ( )

35352534

3

522

55

72772

22

55

113150

1

11

33523

.

11

xxxxxxxx

x

y

x

xx

xxxxx

xx

¢¢

¢

×--×-×--×-

æö

¢

====

ç÷

-

èø

--

----

==

--

Пример 4. Вычислить производную функции, используя правила

дифференцирования и таблицу производных:

1)

5sin

2

log(2);

xx

yx= 2)

2

th

3

ln;

x

y

e

æö

=

ç÷

èø

3)

3

4

2cos2cos

.

log2sin2sin

xx

y

xxx

p

æö

-+

ç÷

èø

=

æö

+-

ç÷

èø

Решение. 1) Преобразуем функцию, пользуясь свойствами лога-

рифма:

5sin55

2222

2

log(2)sinlog(2)sin(loglog2)

sin(5log).

xxxx

yxxxxx

xxx

==×=+=

=+

Полученное выражение дифференцируем по формулам (11.4)–

(11.6) и формулам таблицы производных:

222

2

'(sin(5log))'(sin)'(5log)sin(log)'

5

cos(5log)sin1.

ln2

yxxxxxxxxx

xxxx

x

=+=×++×+=

æö

=+++

ç÷

èø

2) Перед дифференцированием преобразуем выражение, пользуясь

свойствами логарифма:

2

2th2

3

lnln(3)lnln3lnthlnln32lnth.

x

thx

x

yxexxexx

e

æö

==-=+-×=+-

ç÷

èø

Дальше воспользуемся формулами (11.3)–(11.5) и таблицей произ-

водных:

2

21

'(ln32lnth)'(ln3)'2(ln)'(th)'.

ch

yxxxx

x

=+-=+-=-

3) Так как непосредственное дифференцирование вызывает значи-

тельные трудности, предварительно упростим выражение по формулам

тригонометрии:

3

4

44

2222

22

2

2cos2cos

log2sin2sin

2cos2coscos2sinsin

log2sincos2cossin2sin

2coscossin

2sintg

l

log(2cos)

logcossin2sin

xx

y

xxx

xxxx

xxx

xx

xxxx

p

pp

æö

-+

ç÷

èø

==

æö

+-

ç÷

èø

-+

==

æö

+-

ç÷

èø

-+

===

æö

+-

ç÷

èø

3

.

og

x

Полученное выражение дифференцируем по формуле (11.7) и со-

ответствующим формулам таблицы производных:

'

3

2

33

22

3

33

2

3

22

3

11

logtg

(tg)'logtg(log)'

tg

ln3

cos

'

log

loglog

ln3logtgcos

.

ln3logcos

xx

xxxx

x

y

x

xx

xxxx

xxx

×-×

æö

×-×

====

ç÷

èø

×-×

=

××

Задания

I уровень

1.1. Пользуясь определением, найдите производную функции:

1)

32;

yx

=-

2)

2

465;

yxx

=++

3)

1

.

21

y

x

=

-

1.2. Найдите производную функции:

1)

4

3

6

3

2

9;

5

x

yxx

x

=-++

2)

3

2

3

;

4

x

y

xx

+

=

++

3)

2

21

;

3

xx

y

x

--

= 4)

(

)

32

3

2342

;

15

xxx

y

x

+--

=

5)

(

)

2

3

21ñtg

;

3

xx

y

x

-

= 6)

(

)

3

23

3

2

;

24chlog

xx

y

xx

+-

=

185 186

7)

2

(1);

x

yex

=+ 8)

lnarcsin.

yxx

=

1.3. Найдите

(0),

y

¢

если:

1)

3

6530

199;

yxxx

=+-

2)

3

(23)(1);

yxx

=-×-

3)

2

(2);

yxxx

=- 4)

sh1

;

ch

x

y

x

+

=

5)

tg

;

tg

x

ex

y

ex

-

=

+

6)

cos1

.

cos1

x

y

x

-

=

+

1.4. Вычислите:

1)

(

)

(

)

02,

fg

¢¢

- если

(

)

32

34,525,

fxxxx

=-++

()

2

;

1

x

gx

x

=

-

2)

'(1)'(1),

fg

+

если

3

2

254

()410,

fxx

x

=+-+-

3

()();

gxxxx

=-

3)

(

)

(

)

11,

ff

¢¢

+-

если

(

)

53

25.

fxxxx

=+-+

1.5. Вычислите

'(2),

f если

5

2lg1

()log2.

lg4

x

fxx

e

=-+

1.6. Вычислите

'(0),

f если

3

1sin

().

cos

xx

fx

x

++

=

1.7. Решите уравнение:

1)

'()0,

fx

=

где

3

810

()2;

33

fxxx=-+

2)

'()0,

fx

=

где

432

11449

()2.

432

fxxxx

=---+

II уровень

2.1. Найдите производную

',

y

предварительно преобразовав

выражение:

1)

;

1

xx

ee

y

x

-

+

=

-

2)

2

541

;

561

xx

y

xx

+-

=

-+

3)

;

xx

ee

y

ee

-

=

+

4)

3

6323

log

433

(2)(24)

9.

(2816)

x

xxxx

y

xxx

-×++

=×

--+

2.2. Для функции

2

()ln(1ln)

fxxx

=+ найдите

'(1).

f

2.3. Известно, что

()

2sin23cos.

2

fxxx

p

=++

Найдите

.

6

f

p

æö

¢

ç÷

èø

2.4. Решите неравенство

(

)

(

)

,

fxgx

¢¢

> где

(

)

2

2,

fxxx=+-

(

)

2

32.

gxxx=++

III уровень

3.1. Вычислите

0

(),

fx

¢

если:

1)

(

)

(

)

2coscos0,5,

fxxx

=-

0

;

2

x

p

=

2)

(

)

(

)

2sinsin0,5,

fxxx

p

=-

0

.

x

p

=

3.2. Пользуясь определением производной, найдите

(

)

,

fx

¢

если

()

3

sin

5

1, åñëè 0,

0, åñëè 0.

xx

ex

fx

x

×

ì

ï

-¹

=

í

ï

=

î

3.3. Найдите значение производной функции

()

cos

2

fxx

p

æö

=+

ç÷

èø

в точке

,

x

a

=

если

1

tg.

22

a

=

3.4. Найдите сумму значений производной функции у(х) в

точках x = 1 и x = 0, если

3

cos, ïðè 0,

0, ïðè 0.

xxx

y

x

ì

¹

ï

=

í

=

ï

î

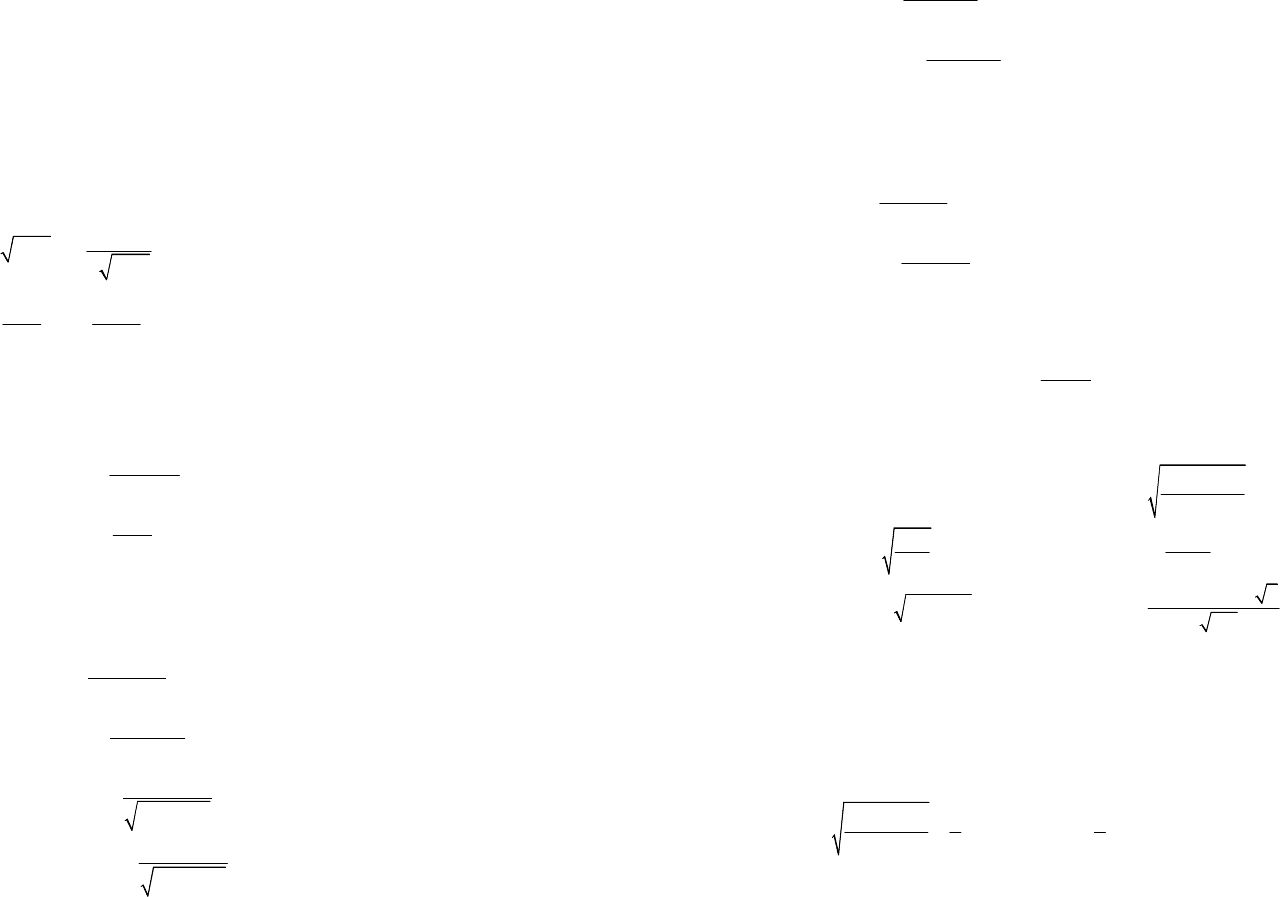
187 188

11.2. Производная сложной функции

Если

(

)

yfu

= и

(

)

ugx

= – дифференцируемые функции

своих аргументов, то производная сложной функции

(

)

(

)

yfgx

=

вычисляется по формуле

().

xu

yfgx

¢

¢¢

=× (11.8)

Обобщенная таблица производных

( )

1

()(),

uxxux

aa

a

-

¢

=× где

,

a

Î

R

в частности:

( )

1

()(),

2()

uxux

ux

¢

=×

2

11

();

()

ux

¢

æö

¢

=-×

ç÷

èø

( )

()()

ln(),

uxux

aaaux

¢

=× где

0,

a

>

1,

a

¹

в частности,

(

)

()()

();

uxux

eeux

¢

=×

( )

1

log()(),

()ln

a

uxux

uxa

¢

=× где

0,0,

xa

>>

1,

a

¹

в част-

ности,

( )

1

ln()();

()

uxux

ux

¢

=×

( )

sin()cos()();

uxuxux

¢

=×

( )

cos()sin()();

uxuxux

¢

=-×

( )

2

1

tg()();

cos()

uxux

ux

¢

=×

()

2

1

ctg()();

sin()

uxux

ux

¢

=-×

( )

2

1

arcsin()();

1()

uxux

ux

¢

=×

-

( )

2

1

arccos()();

1()

uxux

ux

¢

=-×

-

( )

2

1

arctg()();

1()

uxux

ux

¢

=×

+

( )

2

1

arcctg()();

1()

uxux

ux

¢

=-×

+

()

sh()ch()();

uxuxux

¢

=×

( )

ch()sh()();

uxuxux

¢

=×

( )

2

1

th()();

ch()

uxux

ux

¢

=×

( )

2

1

cth()().

sh()

uxux

ux

¢

=-×

Если для функции y = f(x) существует обратная функция

x =

j

(y), которая имеет производную

(

)

0,

y

j

¢

¹

то верна формула

()

1

.

yx

y

j

¢

=

¢

(11.9)

Пример 1. Найти производную функции:

1)

sh2;

x

y = 2)

5

4

2sin

ln;

3

xx

y

xx

-

=

+

3)

1

arcsin;

1

x

y

x

-

=

+

4)

21

lntg;

4

x

y

+

=

5)

( )

2

arccoslg1;

yx

=+

6)

2

3

3cos()arctg

ln.

4sh

xx

y

x

=

Решение. 1) Функцию

sh2

x

y =

необходимо рассматривать как

сложную функцию, где

()sh

yfuu

== и

()2

x

uux

==

– дифференци-

руемые функции своих аргументов. Тогда, согласно формуле (11.8) и

соответствующим формулам таблицы производных, получим:

''()'()(sh)'(2)'ch2ln2ln22ch2.

xxxx

yfuuxuu=×=×=××=××

2) Сначала преобразуем функцию, используя свойства логарифмов:

( ) ( )

5

54

4

2sin11

lnln2sinln3.

22

3

xx

yxxxx

xx

-

==--+

+

Вычисляем производную, используя правило дифференцирования

суммы функций, формулу (11.8) и обобщенную таблицу производных:

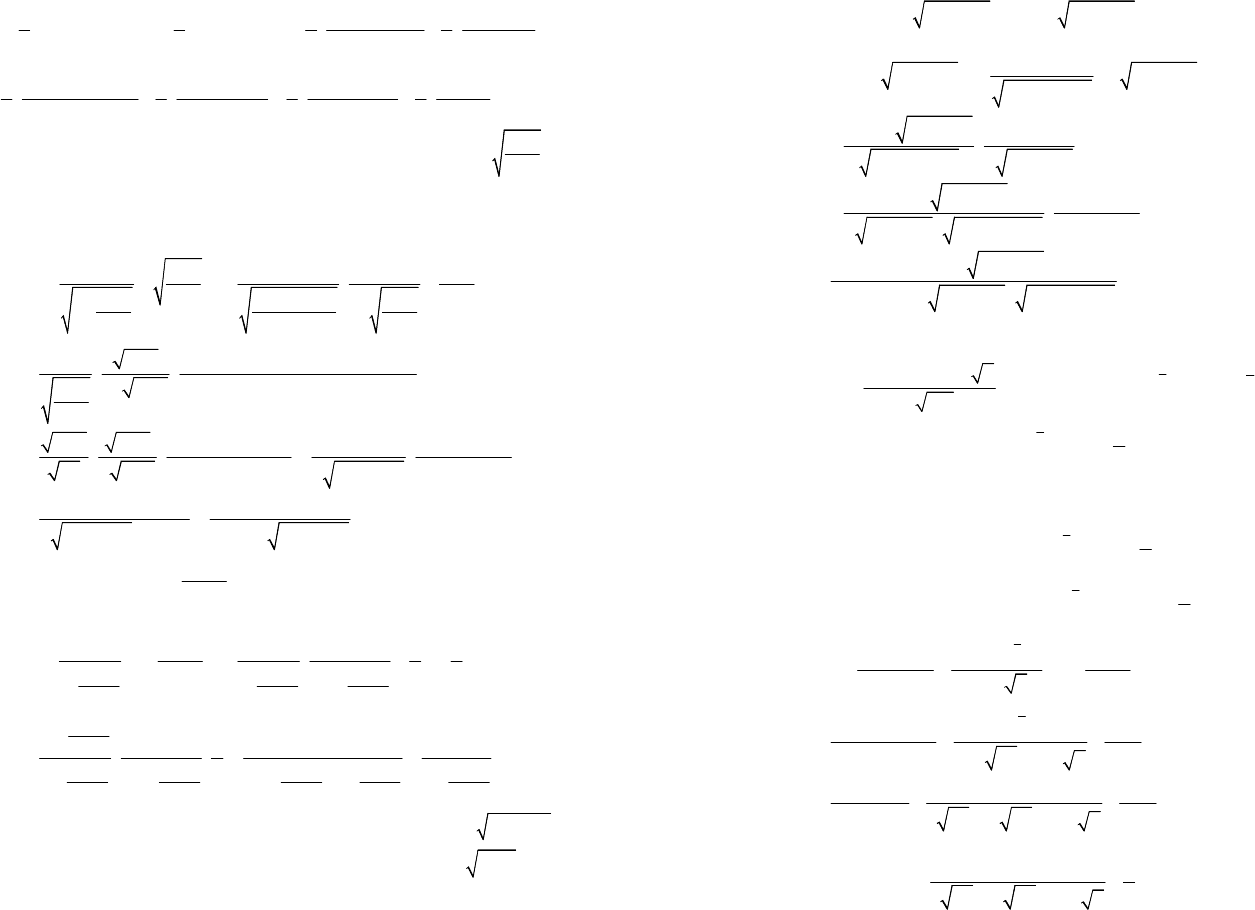
189 190

( )

( ) ( )

( )

54

43

5454

2sin3

1111

ln2sinln3

2222

2sin3

11152cos143

.

2222

2sin32sin3

xxxx

yxxxx

xxxx

xxx

xxxxxxxx

¢¢

-+

¢¢

¢

=--+=×-×=

-+

¢¢

-+

=×-×=×-×

-+-+

3) Рассмотрим функцию как

(

)

arcsin,

ygx

= где

()

1

x

gx

x

-

=

+

–

также сложная функция. Применив формулу (11.8) дифференцирова-

ния сложной функции, обобщенную таблицу производных, а также

правило дифференцирования частного двух функций, получим:

11111

11

1111

12

111

xx

y

xx

xxxx

xxx

¢

æö

+-

æö

¢

=×=××=

ç÷

-+

-+-+-

èø

-×

+++

()()()( )

( )

2

1111

11

221

1

xxxx

x

xx

x

¢¢

-×+--×+

+

=××=

×-

+

(

)

(

)

( )

( )( )( ) ( )

22

11

11111

221

11

21

.

2211121

xx

xxxxx

xx

xxxxxx

-+--

+++--+-

=××=×=

-

++

--

==

-×++×-

4) Пусть

()

21

tg,

4

x

gx

+

= тогда

(

)

ln.

ygx

= Согласно формуле

(11.8), получим:

2

212121

444

21

4

2121212121

44442

1211111

tg

424

tgtgcos

cos

1111

.

2

sincos2sincossin

xxx

x

xxxxx

x

yx

+++

+

+++++

¢¢

+

æöæö

¢

=×=××+=

ç÷ç÷

èøèø

=××==

×

5) Рассмотрим функцию как

()

( )

2

,

ygx=

где

() ( )

arccoslg1.

gxx

=+

Функцию

(

)

gx

можно представить в виде

() ()

,

gxhx

= где

(

)

(

)

lg1.

hxx

=+

Тогда:

( ) ( )

( )

2arccoslg1arccoslg1yxx

¢

=+×+=

( )

( ) ( )

( )

( ) ( )

( )

( ) ( ) ( )

1

arccoslg1lg1

1lg1

arccoslg1

1

lg1

1lg12lg1

arccoslg1

1

1ln10

2lg11lg1

arccoslg1

.

21ln10lg11lg1

xx

x

xx

x

xx

x

xxx

æö

¢

ç÷

=+×-×+=

ç÷

-+

èø

+

¢

=-××+=

-++

+

¢

=-××+=

+

+×-+

-+

=

++×-+

6) Перед тем как дифференцировать функцию, преобразуем выра-

жение, пользуясь свойствами логарифма:

1 1

2

3

2

3

2

1

2

3

3cos()arctg

lnln(3cos()arctg())ln(4sh)

4sh

1

ln3lncos()lnarctg()ln4lnsh.

2

xx

yxxx

x

xxx

==-=

=++--

Продифференцируем полученное выражение по формулам (11.3)–

(11.5), (11.8) и соответствующим формулам таблицы производных:

1

2

3

1

2

3

1

2

3

2

3

1

22

3

2

3

2

3

1

'(ln3lncos()lnarctg()ln4lnsh)'

2

1

(ln3)'(lncos())'(lnarctg())'(ln4)'(lnsh)

'

2

(cos())'(arctg())'(sh)'

00

2sh

cosarctg

sin()'()'ch

2sh

cos

(1)arctg

yxxx

xxx

x

xx

xxxx

x

xx

=++--=

-×

=+-

+

2

33

22

3

2sin1ch

.

2sh

cos

3(1)arctg

xxx

x

xxx

=

-

=+-

+

Применив далее формулы тригонометрии, окончательно получим:

2

33

22

3

11

'2tgcth.

2

3(1)arctg

yxxx

xxx

=-+-

+

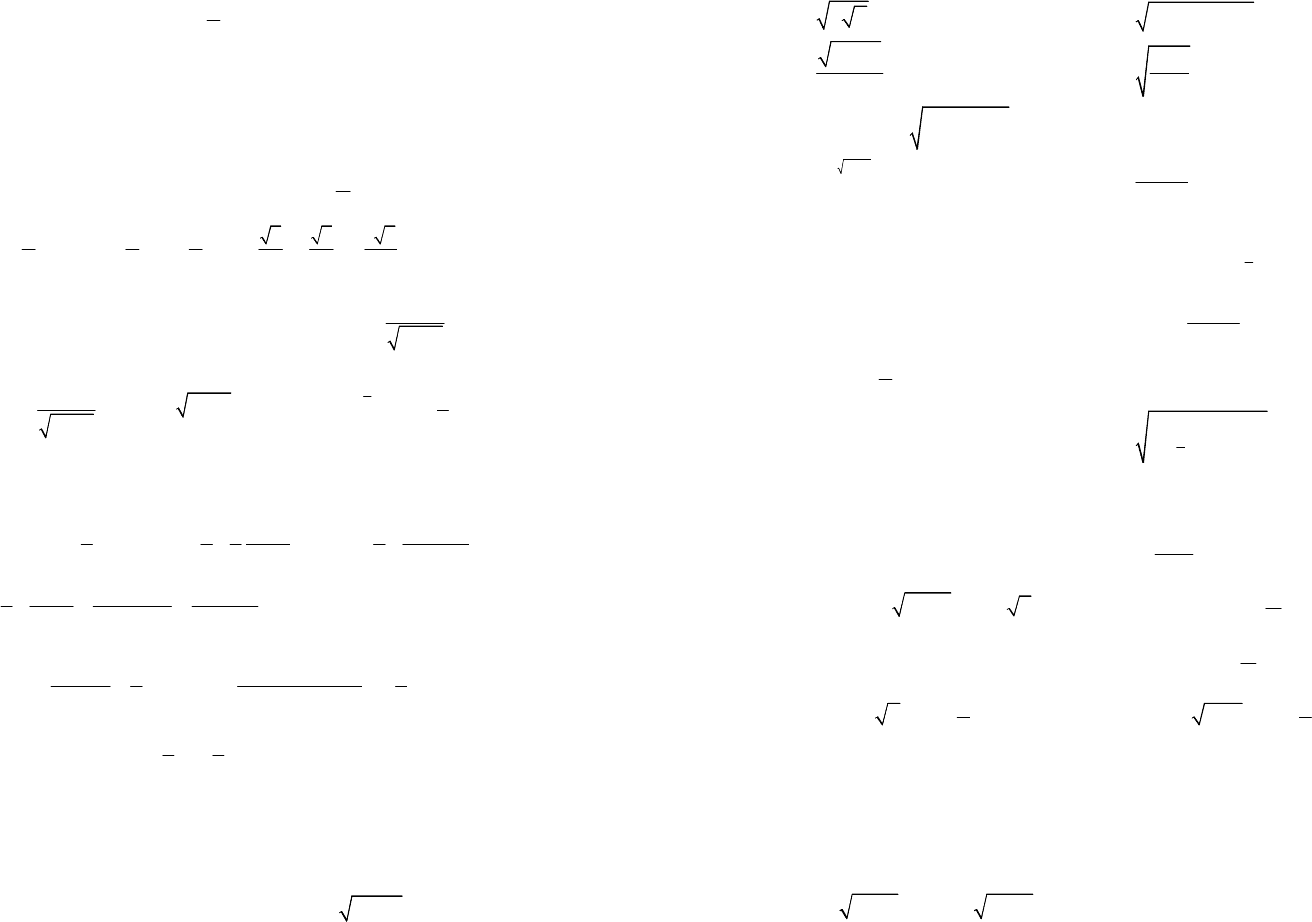
191 192

Пример 2. Вычислить

',

4

y

p

æö

ç÷

èø

если

3

cos.

y

j

=

Решение. Это сложная функция с промежуточным аргументом

cos.

j

Дифференцируем ее по формуле (11.8). При этом пользуемся пер-

вой формулой обобщенной таблицы производных при условии

3:

a

=

( )

322

cos3coscos3cossin.

y

jjjjj

¢

===-×

Вычислим значение производной при

:

4

p

j

=

2

2232

'3cossin3.

444224

y

ppp

æö

æöæöæö

=-×=-×=-

ç÷

ç÷ç÷ç÷

ç÷

èøèøèø

èø

Пример 3. Вычислить

'(1)'(1),

yy

--

если

2

ln.

1

x

y

x

=

+

Решение. Преобразуем функцию, используя свойства логарифмов:

1

222

2

1

lnlnln1lnln(1)lnln(1).

2

1

x

yxxxxxx

x

==-+=-+=-+

+

Теперь продифференцируем выражение по формулам (11.3),

(11.5), (11.8) и соответствующим формулам таблицы производных.

Функцию

2

ln(1)

yx

=+ рассмотрим как

()ln,

yfuu

== где

2

1.

ux

=+

22

111111

(ln)(ln(1))··(1)·2

22

12(1)

yxxxx

xx

¢¢¢¢

=-+=-+=-=

++

22

222

111

.

1(1)(1)

xxx

x

xxxxx

+-

=-==

+++

Теперь вычислим

2

11

'(1)

2

1(11)

y

==

+

и

( ) ( )

( )

2

11

'(1).

2

111

y

-==-

-×+-

Тогда

11

'(1)'(1)1.

22

yy

æö

--=--=

ç÷

èø

Задания

I уровень

1.1. Найдите производную функции:

1)

28

(243);

yxx=+- 2)

2

9;

yx

=-

3)

3

;

yxx

= 4)

234

5

(24);

yxx=-

5)

2

5

;

5

x

y

x

-

=

+

6)

1

;

1

x

y

x

+

=

-

7)

( ) ( )

2

33

3

82174;

yxx=-×+

8)

ln

3;

x

y =

9)

2

4

10

3;

xx

y

+

= 10)

cos3

;

x

y

x

=

11)

32

sin5;

yx

=

12)

2

ctgtg3;

yx

=

13)

2

arccos2;

yx

= 14)

2

(1tg3)·;

x

yxe

-

=+

15)

arcsin2;

yxx

=

16)

2

arcsin;

2

x

y

x

-

=

+

17)

3

arccos;

2

x

y = 18)

2

ln(1)2arctg;

xx

yee

=+-

19)

34

2

log;

yx

= 20)

( )

3

1

2

log2.

yx=-+

1.2. Найдите производную функции при данном значении

аргумента:

1)

22

0

(), 0;

t

fttet

=+=

2)

0

1

()ln, 3;

1

x

fxx

x

-

==

+

3)

2

0

()(1)1, 2;

fxxxx=+×-=

4)

0

()lncos, ;

3

fxxx

p

==-

5)

2

0

()sincos, 0;

ftttt

=-=

6)

cos2

0

(), ;

4

y

fyey

p

==

7)

0

1

()arctg, ;

4

fxxx

==

8)

0

1

()arccos1, .

2

fxxx

=-=

1.3. Решите неравенство

(

)

(

)

,

fxgx

¢¢

>

если

(

)

(

)

ln5

fxxx

=+-

и

(

)

(

)

ln1.

gxx

=-

II уровень

2.1. Вычислите

,

y

¢

если

1)

ln(11)ln(11);

xx

yee

=+--++

2)

2

lnlnln;

yxx

=-

193 194

3)

3

lnlg(32);

yx

=- 4)

3

logln(32);

yx=+

5)

235

logloglog;

yx

=

6)

2

tgsincos;

yx

=

7)

3

ctglogsin2;

yx

= 8)

23

(72)sin;

2

x

yx=-

9)

(

)

2

ln1arcsin;

xxx

yeee

-

=+-+ 10)

1

arctg;

1

x

y

x

-

=

-

11)

2

3

31

log(2);

31

x

yxx

x

+

=-

-

12)

3

arcctg(34)

;

(2)

x

y

x

+

=

+

13)

22

(34)tg;

2

x

yx=- 14)

cos

3

(3)2.

x

yxx=+

2.2. Вычислите производную функции при заданном значе-

нии аргумента:

1)

2

arctgln(1),

yxxx

=++

0

1;

x

=

2)

arctg51ln,

yxxx

=-+

0

1;

x

=

3)

2

1

arccos,

12

y

x

æö

=

ç÷

+

èø

0

2;

x

=

4)

2

1

arctg,

x

y

x

-

=

0

1;

x

=

5)

(ch22sh2),

x

yexx

=+

0

0;

x

=

6)

4

ln(1)arctg,

yxx

=++

0

1;

x

=

7)

2

44arcsin,

2

x

yxx=×-+

0

0;

x

=

8)

2

12

ln(3),

x

yex

-

=++

0

1.

x

=

2.3. Вычислите значение производной

0

'(),

fx

предваритель-

но упростив выражение:

1)

33

0

(), 0;

3

xx

ee

fxx

-

==

2)

0

(), 0;

xx

ee

fxx

ee

-

==

+

3)

0

22

(), 1;

xx

ee

fxx

ee

-

+

==

-

4)

22

0

(), 1.

4

xx

xexe

fxx

-

+

==-

2.4. Вычислите производную функции, предварительно уп-

ростив выражение:

1)

2

1

ln;

1

x

y

x

+

=

-

2)

121

lnarctg;

223

x

yx

x

+

=-

-

3)

3

4

3

logln3;

8cos

x

y

x

+

=+ 4)

(

)

4

233

4

5

ctg4

lnsinln5.

2

x

ex

y

x

+

×+

=+

-

2.5. Известно, что

3

1

()1

2

fxx

=+

и

().

x

gxxe

-

=× Найдите

значение выражения

0

(),

fx

¢

где

0

(0).

xg

¢

=

2.6. Найдите производную функции

(

)

()(),

gxffx

= если

2

()sin.

fxx

=

2.7. Найдите производную функции

1

(),

gxf

x

-

æö

=

ç÷

èø

если

2

()cos.

fxx

=

2.8. Докажите тождество:

1)

(0)

()2()(0)1,

3

f

fxxfxf

¢¢

=+-=

если

2

()3;

x

fxe

=

б)

11

()()0,

fxfxf

xx

æö

¢

++-=

ç÷

èø

если

()ln.

fxx

=

Ш уровень

3.1. Найдите производную функции:

1)

2

arcsin

ln1;

1

xx

yx

x

=+-

-

2)

( )

42

sh3sh3

arctgsh;

8

4ch8ch

xx

yx

xx

=++

3)

2

1cos3

cosln2;

3sin6

x

y

x

=- 4)

11th

lnarctgth.

2

1th

x

yx

x

+

=-

-

3.2. Найдите производную функции, предварительно преоб-

195 196

разовав выражение по тригонометрическим формулам:

1)

4cos2sin3cos;

yxxx

=

2)

coscoscos;

234

xxx

y =

3)

(

)

2coscos3

;

2sin2sin4

xx

y

xx

+

=

+

4)

2sinsin3sin5

;

cos2cos2cos3

xxx

y

xxx

-+

=

-+

5)

sinsin

11

2

1tg21tg2;

cos2cos2

1coscos

2

x

yxx

x

xx

x

+

æöæö

=++×-+

ç÷ç÷

èøèø

++

6)

222

sin(4)coscos(4)sinsin.

2

x

yxxxxxx=+-++

3.3. Дана функция

sincos

().

sincos

xx

fx

xx

-

=

+

Определите, чему

равно значение выражения

1

(0)()cos22().

24

ffxxffx

p

æö

¢¢¢

---

ç÷

èø

3.4. Даны функции

22

()2cos

2

x

fxx

æö

=

ç÷

èø

и

2

()sin.

gxxxx

=-

Найдите количество значений x на отрезке

[

]

;,

pp

- для которых

выполняется равенство

'()().

fxgx

=

11.3. Уравнение касательной

и нормали. Физический смысл производной

Производная функции

(

)

yfx

=

в точке

0

x

представляет со-

бой угловой коэффициент касательной, проведенной к графику

функции в точке

(

)

(

)

00

;:

xfx

(

)

0

tg,

fx

a

¢

=

где

a

– угол наклона касательной к оси Ox. В этом состоит

геометрический смысл производной.

Уравнение касательной, проведенной к графику функции

в точке

(

)

000

;,

Mxy

где

(

)

00

,

yfx

= имеет вид:

(

)

(

)

(

)

000

.

yfxxxfx

¢

=×-+ (11.9)

Прямая, проходящая через точку

(

)

000

;

Mxy

графика функ-

ции

(

)

yfx

= перпендикулярно касательной, проведенной в

этой точке, называется нормалью к графику функции

(

)

yfx

=

в точке

(

)

000

;

Mxy

(рис. 11.1). Уравнение нормали имеет вид:

( )

( ) ( )

00

0

1

,

yxxfx

fx

=-×-+

¢

(11.10)

где

(

)

0

0.

fx

¢

¹

Рис. 11.1

Физические приложения производной

1. Если материальная точка M движется неравномерно по

пути, заданному функцией

(

)

,

ySt

= то мгновенная скорость

движения в момент времени

0

t

есть производная от пути S по

времени t:

(

)

(

)

00

.

vtSt

¢

=

(11.11)

2. Если функцией

(

)

yvt

= описывается процесс изменения

скорости неравномерного движения в зависимости от времени,

то мгновенное ускорение материальной точки в момент времени

0

t

есть производная от скорости v по времени t:

(

)

(

)

00

.

atvt

¢

= (11.12)

3. Если

(

)

yQT

=

– функция, описывающая процесс измене-

М

0

у

х

0

у

0

х

0

a

y = f(x)

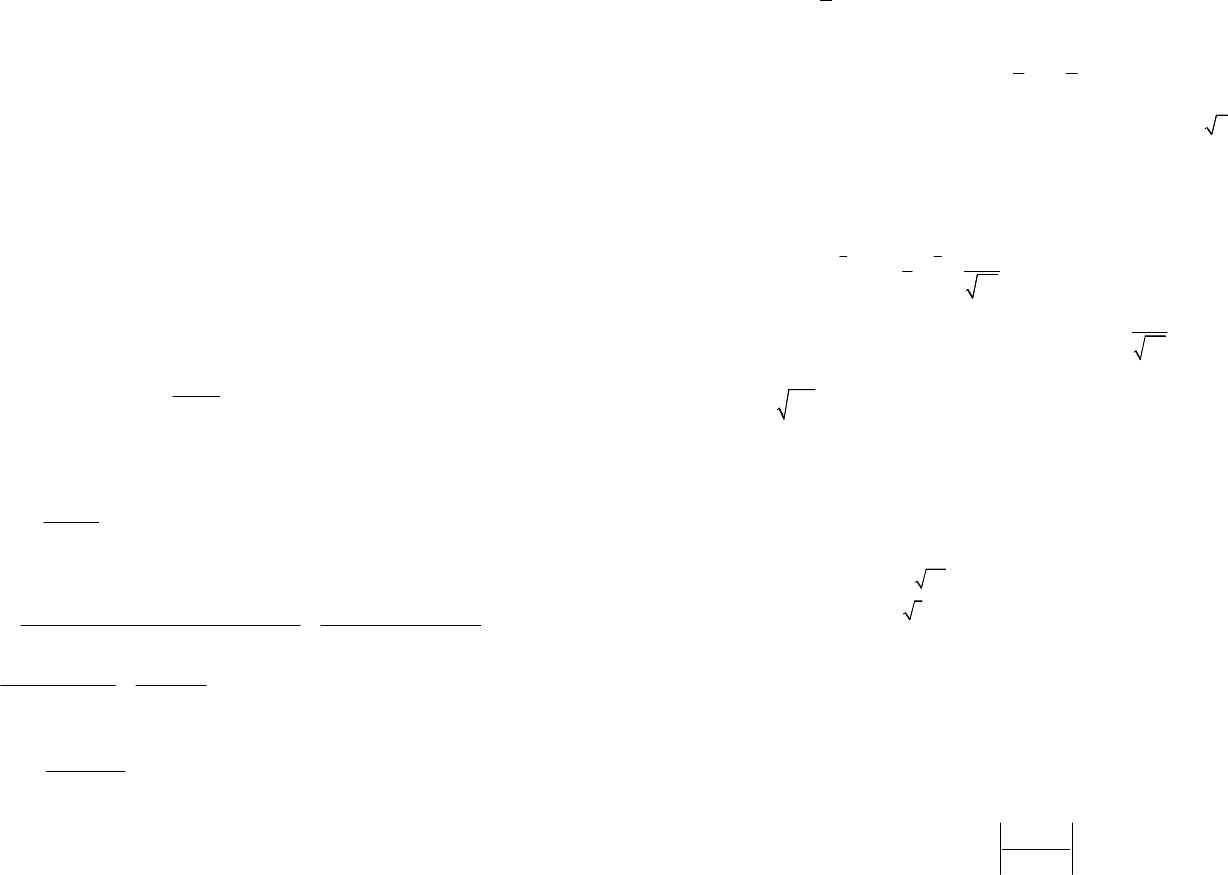
197 198

ния количества теплоты, сообщаемой телу при нагревании его

до температуры T, то теплоемкость тела есть производная от

количества теплоты Q по температуре T:

(

)

(

)

00

.

CtQT

¢

=

4. Линейная плотность неоднородного тонкого стержня в

точке

0

x

есть производная от массы m по длине l:

(

)

(

)

00

.

xmx

r

¢

=

5. Мгновенное значение электродвижущей силы индукции

равно скорости изменения магнитного потока, т. е. производной

от магнитного потока

f

по времени t:

(

)

(

)

00

.

tt

ef

=

6. Сила тока в колебательном контуре в момент времени t

0

равна производной заряда q по времени t:

(

)

(

)

00

.

Itqt

¢

=

Пример 1. Написать уравнение касательной и нормали, проведен-

ной к графику функции

43

32

x

y

x

-

=

-

в точке с абсциссой x = 2.

Решение. Для нахождения уравнения касательной воспользуемся

формулой (11.9). Сначала найдем ординату точки касания

0

().

fx

Для

этого значение

2

x

=

подставим в уравнение функции:

()

423

25.

322

f

×-

==-

-×

Для нахождения углового коэффициента найдем производную

',

y

используя формулу дифференцирования дроби:

(

)

(

)

(

)

(

)

( )

(

)

(

)

( )

( ) ( )

22

43'324332'432243

3232

128866

.

3232

xxxxxx

y

xx

-×---×--+-

¢

===

--

-+-

==

--

Найдем значение производной при

2:

x

=

()

( )

2

6

26.

322

y

¢

==

-×

Подставив найденные значения в формулу (11.9), получаем урав-

нение касательной:

(

)

625,

yx

=--

т. е.

617.

yx

=-

Чтобы написать уравнение нормали, воспользуемся формулой (11.10):

1

(2)5.

6

yx

=---

Получим, что уравнение нормали, проведенной к заданной кривой

в заданной точке, имеет вид

12

4.

63

yx=--

Пример 2. Определить, в какой точке кривой

3

yx

= касатель-

ная наклонена к оси абсцисс под углом 45°.

Решение. Так как тангенс угла наклона касательной к оси абсцисс

равен значению производной в точке касания, найдем производную

функции:

12

33

3

2

11

33.

3

yxx

x

-

¢

æö

ç÷¢

==×=

ç÷

èø

По условию

0

()tg45.

yx

¢

=°

Следовательно,

3

2

1

1.

x

=

Отсюда:

2

3

0

1,

x

=

2

0

1,

x

=

0

1.

x

=±

Получили два значения абсциссы точки касания:

01

1,

x

=-

02

1,

x

=

т. е. существуют две точки касания, в которых касательная образует

угол 45° с осью Ох.

Найдем соответствующие ординаты точек касания, подставляя

значения

0102

,

xx

в формулу функции:

3

01

()(1)313;

yxy

=-=-=-

3

02

()(1)313.

yxy

===

Приходим к ответу: в точках

01

(1; 3)

M

--

и

02

(1; 3)

M

касатель-

ная к заданной кривой образует с осью Ох угол 45°.

Пример 3. Найти острый угол между параболами

2

3

yx

=-

и

2

4

yx

=-

в точке их пересечения, имеющей отрицательную абсциссу.

Решение. Угол между двумя кривыми в точке их пересечения –

это угол между касательными к этим кривым, проведенными в точке

их пересечения. Тангенс этого угла вычислим по формуле

21

12

tg,

1

kk

j

-

=

+×

(11.13)

Майсеня Л.И. Математика в примерах и задачах. Часть 2

Подождите немного. Документ загружается.