Майсеня Л.И. Математика в примерах и задачах. Часть 1
Подождите немного. Документ загружается.


156 157
Пример 1. Построить график функции:
1)
( )
5
12;
yx
=--
2)
4
42.
yx
=--
Решение. 1) Для построения графика данной функции используем
правила преобразования графиков:
а) строим график функции
5
yx
=
(он показан на рис. 5.7);
б) график функции
5
(1)2
yx
=--
получаем из графика функции
5
yx
=
путем параллельного переноса его на одну единицу вправо по
оси Ох и на две единицы вниз по оси Оу;
в) график исходной функции получаем из графика функции
5
(1)2:
yx
=--
оставляем ту часть графика, которая находится справа
от оси Оу и на оси Оу, другую – отбрасываем (на рис. 5.8 она показана
пунктиром). Оставшуюся часть графика дополняем симметричной ей
относительно оси Оу (рис. 5.8).
Рис. 5.8
2) Преобразуем функцию к виду
4
(4)2.
yx
=---
Заметим, что
(
]
();4.
Dy =-¥ График этой функции получаем путем следующих
преобразований:
а) строим график функции
4
;
yx
=
б) график
4
yx
=-
получаем из предыдущего симметричным ото-
бражением относительно оси Оу;
в) график функции
4
(4)
yx
=--
получаем из предыдущего сме-
щением на 4 единицы вправо по оси Ох;
г) график заданной функции получаем из графика функции
4
(4)
yx
=--
параллельным переносом его на две единицы вниз по
оси Оу (рис. 5.9).
Рис. 5.9
Задания
I уровень
1.1. Определите, принадлежит ли точка
(
)
;
Mxy
графику
функции
():
yfx
=
1)
5
3
11, (1; 21);
2
x
yM
+
æö
=-
ç÷
èø
2)
4
328
, (2; 17);
4
xx
yM
+-
=-
3)
4
7, (3; 2);
yxM=+- 4)
6
13, (5; 3).
yxM=--
1.2. Найдите область определения функции:
1)
3
653
;
2
x
y
xxx
=
-+
2)
4
2
2
;
9
x
y
x
+
=
-
3)
7
5
2
35
;
56
xx
y
xx
++
=
++
4)
8
2
4
2
2
.
16
x
y
x
+
=
-
1.3. Постройте график функции и определите область ее зна-
чений:
1)
5
3;
yx
=+
2)
3
2;
yx
=-
3)
3
278;
yx
=-
4)
1
7
4.
yx
=-
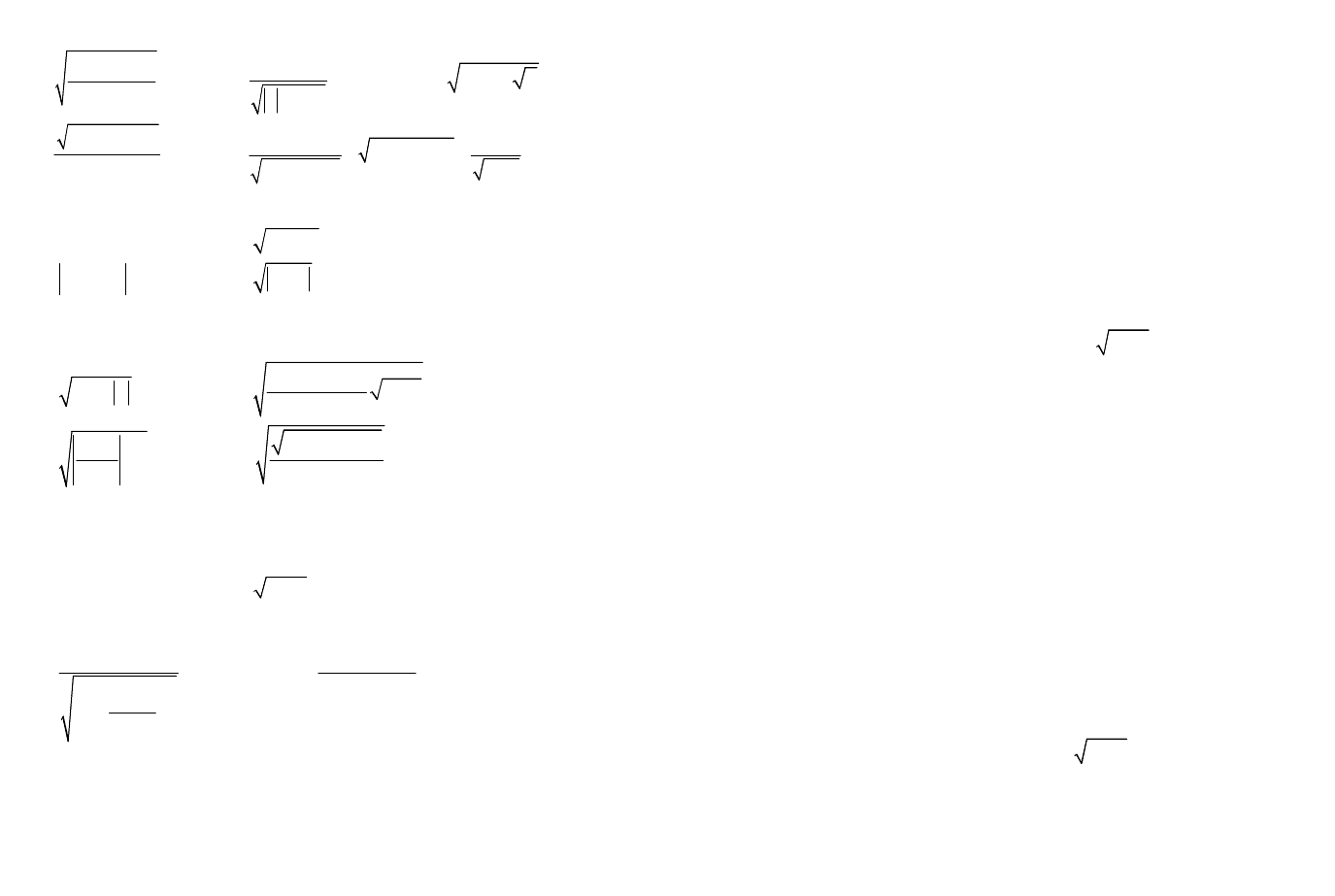
158 159
II уровень
2.1. Найдите область определения функции:
1)
2
8
2
712
;
32
xx
y
xx
++
=
--
2)
5
3
3
;
(1)
x
y
xx
+
=
+
3)
4
8
(3);
yxx
=-
4)
10
1811
2
67
;
45
xx
y
xx
++
=
+-
5)
6
2
5
42
13
514.
2
20
yxx
x
xx
=++-+
-
+-
2.2. Постройте график функции:
1)
4
(3)2;
yx
=-+
2)
4
(3)1;
yx
=+-
3)
7
(2);
yx=-
4)
4
3.
yx
=+
III уровень
3.1. Найдите область определения функции:
1)
8
2;
yxx
=- 2)
2
6
2
68
3;
56
xx
yx
xx
-+-
=-
++
3)
8
2
1;
3
x
y
x
+
=-
-
4)
2
12
2
673
.
328
xx
y
xx
+-
=
-++
3.2. Найдите функцию, обратную данной. Укажите область
определения и область значений обеих функций. Постройте гра-
фики данной функции и обратной в одной системе координат:
1)
3
(2);
yx=+ 2)
4
2.
yx
=+
3.3. Найдите множество значений функции:
1)
2
2
2
2
;
1
1
1
x
y
x
x
=
æö
-
-
ç÷
+
èø
2)
42
2
45
.
44
xx
y
x
+-
=
-
5.4. Иррациональные уравнения
Иррациональным уравнением называется уравнение, со-
держащее неизвестную под знаком корня или под дробным по-
казателем. (В этом параграфе термин «корень» будет соответст-
вовать операции извлечения корня с определенным показателем,
в отличие от термина «решение»).
Основной метод решения таких уравнений – возведение
обеих частей уравнения в одну и ту же степень, чтобы корни ис-
чезли. Иногда приходится возводить в степень несколько раз.
При этом следует анализировать, какие корни надо оставлять в
левой части уравнения, а какие корни перенести в правую часть
(если корней несколько). От этого часто зависит рациональность
решения.
Поскольку корни нечетной степени определены для любых
по знаку подкоренных выражений и принимают любые по знаку
значения, то возведение уравнения в нечетную степень является
равносильным преобразованием (т. е. мы не теряем решений и
не получаем посторонних).
Корни с четным показателем
2
(), ,
n
fxn
Î
N
определены
для f(x) ³ 0. Возведение уравнения, содержащего такие корни, в
четную степень может изменить ОДЗ уравнения и привести к
посторонним решениям. В таком случае итоговым моментом в
решении уравнения является проверка полученных решений
подстановкой в заданное уравнение. Проверка решения по ОДЗ
такого уравнения недостаточна.
ОДЗ иррационального уравнения следует находить в том
случае, если предполагается, что она состоит только из несколь-
ких чисел или может быть пустым множеством. Если ОДЗ со-
стоит из одного, двух и т. д. чисел, то уравнение можно не ре-
шать, а эти числа проверять (являются ли они решением) под-
становкой в заданное уравнение.
Если ОДЗ есть пустое множество, то уравнение не имеет
решений.
При решении иррациональных уравнений используют также
метод замены переменной и другие методы.
Если имеется уравнение вида
2
(),
n
fxc
=
где с < 0, то оно не
имеет решений, так как корни с четным показателем понимаем в
арифметическом смысле, т. е. как неотрицательные.
Некоторые типы иррациональных уравнений
Пусть далее
(),(),()
fxgxhx
– некоторые выражения с не-
известной х,
.
n
Î
N
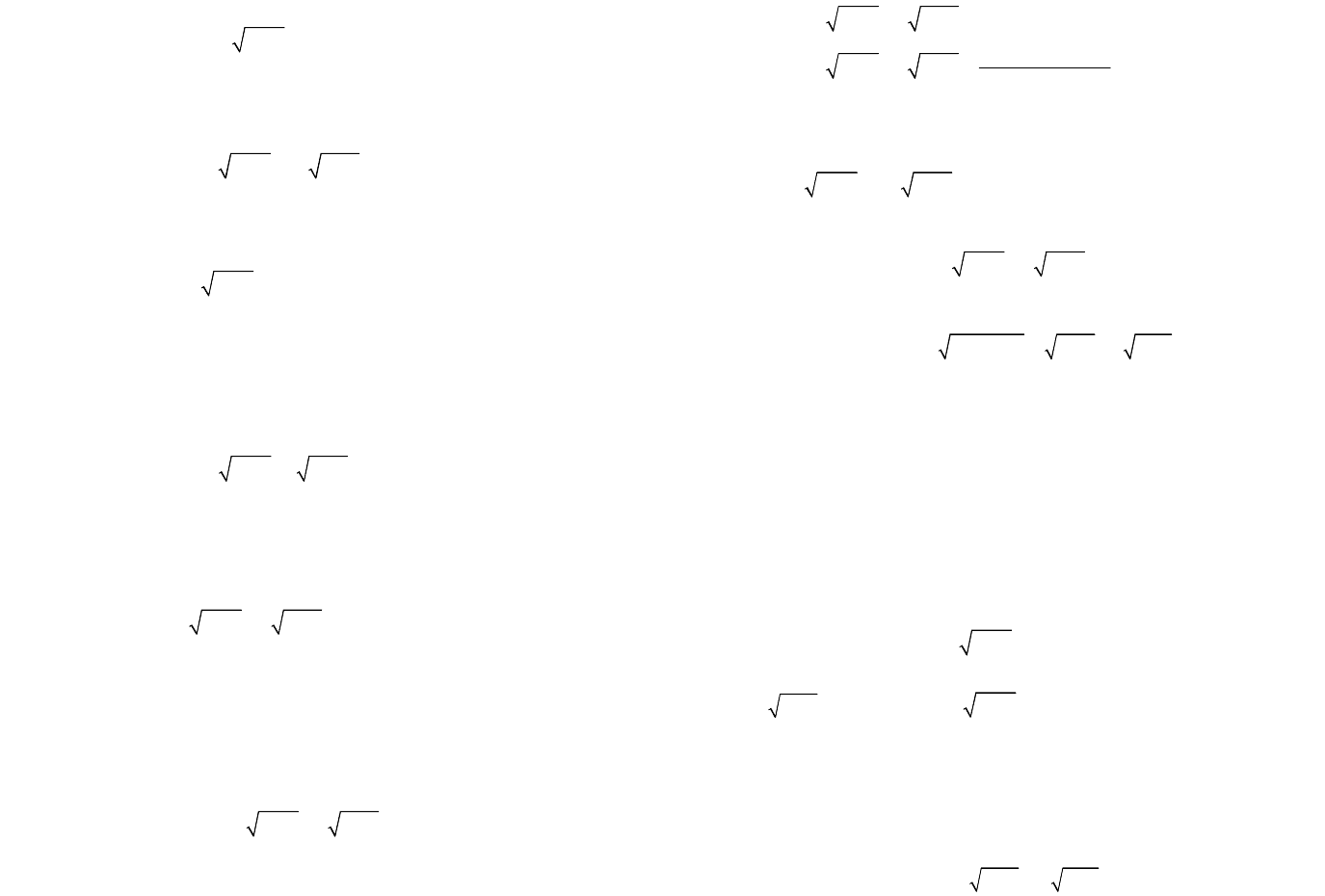
160 161
I тип: уравнение вида
21
()().
n
fxgx
+
=
(5.1)
Возведение в
(
)
21
n
+
-ю степень приводит к равносильному
уравнению
( )
21
()().
n
fxgx
+
=
Уравнение
2121
()()
nn
fxgx
++
= (5.2)
после возведения в
(
)
21
n
+
-ю степень сводится к равносильно-
му уравнению
()().
fxgx
=
Уравнение
2
()(),
n
fxgxn
=Î
N
(5.3)
после возведения в степень 2n приводит к уравнению-следствию
( )
2
()().
n
fxgx= (5.4)
Найденные корни уравнения (5.4) проверяют подстановкой
в уравнение (5.3) и отбирают те из них, которые удовлетворяют
уравнению (5.3).
Уравнение
22
()()
nn
fxgx
= (5.5)
после возведения в степень 2n сводится к уравнению-следствию
()().
fxgx
=
(5.6)
Корни уравнения (5.6) необходимо проверить подстановкой
в уравнение (5.5).
II тип: уравнение вида
()()(),
afxbgxhx
+= (5.7)
где
,.
ab
Î
R
1-й способ. Необходимо возвести уравнение (5.7) в квадрат.
В определенных случаях следует один из корней перенести в
правую часть уравнения. После упрощения полученное уравне-
ние возводят в квадрат еще раз.
2-й способ. Умножение уравнения (5.7) на сопряженное вы-
ражение
(
)
22
()()()()().
afxbgxhxafxbgx
-=-
Отдельно проверяют, имеет ли решение уравнение h(x) = 0.
Затем для h(x) ¹ 0 рассматривают систему
22
()()(),
()()
()().
()
afxbgxhx
afxbgx
afxbgx
hx
ì
+=
ï
í
-
-=
ï
î
Сложение уравнений этой системы приводит к уравнению
вида (5.3).
3-й способ. Замена переменных
(),()
fxugxv
==
и переход к системе уравнений относительно u, v.
Уравнение
33
()()(),
afxbgxhx
+= (5.8)
где a, b Î R, возведением в куб обеих частей сводится к
уравнению
(
)
( )
3
33
333
()()3()()()()().
afxbgxabfxgxafxbgxhx+++=
(5.9)
Выражение в скобках (в левой части уравнения (5.9)) заме-
няют на
(),
hx
используя заданное уравнение. В итоге заданное
уравнение (5.8) приводится к уравнению-следствию, которое
снова возводят в куб.
Полученные таким образом решения необходимо проверить
подстановкой в уравнение (5.8).
III тип: уравнения, решаемые заменой переменной.
В результате замены может уменьшиться степень выраже-
ний, стоящих под корнями, что приведет к уменьшению степени
рационального уравнения после избавления от корней.
Если уравнение имеет вид
(
)
()0,
n
Ffx
=
2,3,...,
n
=
(5.10)
где F – некоторое алгебраическое выражение относительно
(),
n
fx
то заменой
()
n
yfx
= оно сводится к уравнению
()0.
Fy
=
(5.11)
После решения уравнения (5.11) возвращаются к старой пе-
ременной и находят решения уравнения (5.10).
IV тип: уравнения, решаемые исходя из арифметического
смысла корней с четными показателями. В частности, решение
уравнения
22
()()0,
nn
afxbgx
+=
(5.12)
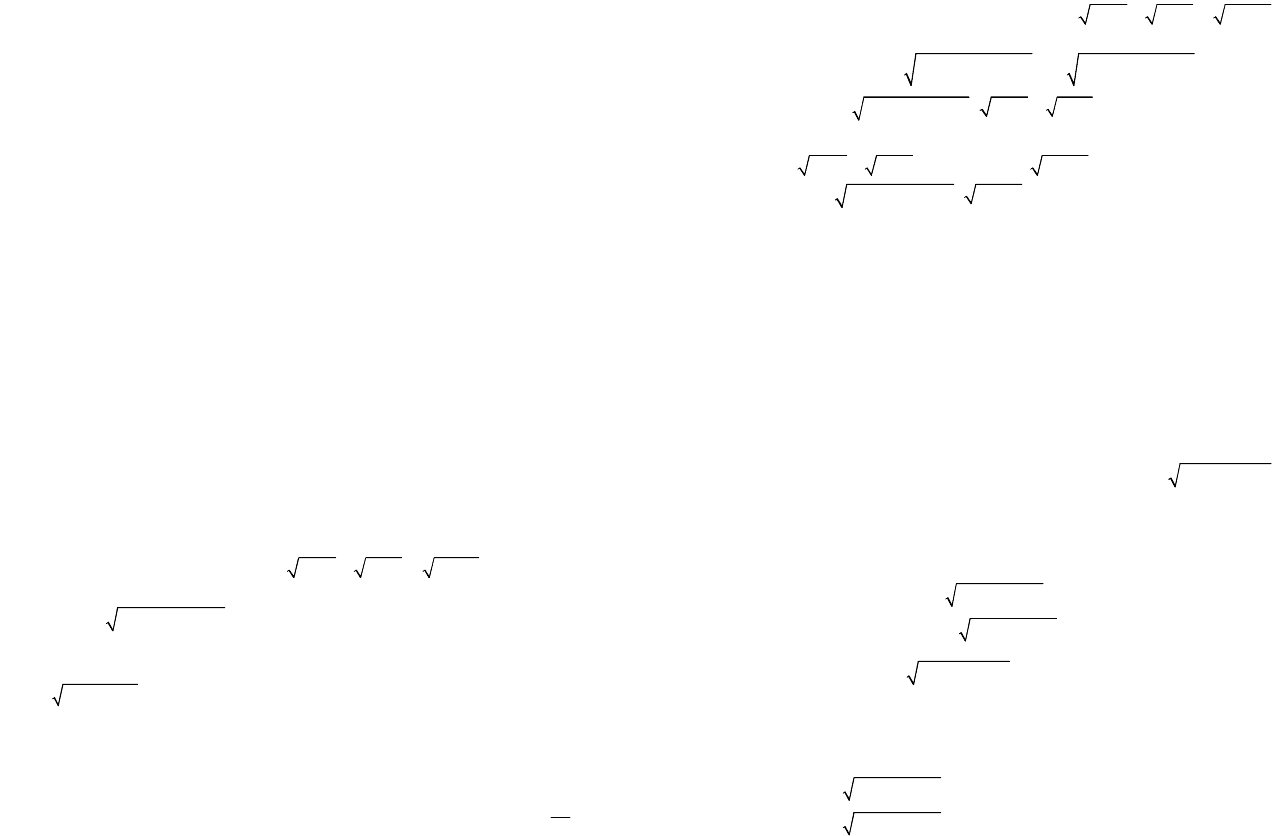
162 163
где a > 0, b > 0, сводится к решению системы
()0,
()0.
fx
gx
=
ì
í
=
î
V тип: уравнения, решаемые функциональными методами и
методами, основанными на ограниченности входящих в уравне-
ние функций.
Решение уравнений основывается на следующих утвержде-
ниях.
1. Если ()
fxa
³
и ()
gxa
£
для всех Xx
Î
, то на множест-
ве X уравнение f(x) = g(x) равносильно системе уравнений
î
í
ì
=
=
.)(
,)(
axg
axf
2. Если функции f(x) и g(x) непрерывны и f(x) возрастает, а
g(x) убывает для x Î X, то уравнение f(x) = g(x) имеет не больше
одного решения на промежутке X. Если один корень подобрать,
то других корней нет.
3. Если f(x) – возрастающая функция, то уравнение
(
)
()
ffxx
=
равносильно уравнению
().
fxx
=
4. Если f(x) – возрастающая (убывающая) функция, то урав-
нение
()()
fxfy
=
равносильно уравнению
.
xy
=
Пример 1. Решить уравнение
4335.
xxx
-++=-
Решение. Возведем обе части уравнения в квадрат:
42(4)(3)335.
xxxxx
-+-×+++=-
Приводим подобные. При этом в левой части уравнения записыва-
ем корень, остальные слагаемые – в правой части:
2
2324.
xxx
-+=-
Возводим полученное уравнение в квадрат еще раз:
22
2
4(12)816,
34640.
xxxx
xx
--=-+
+-=
Решая последнее квадратное уравнение, находим корни
1
16
,
3
x =-
2
4,
x
=
которые теперь необходимо проверить. Делаем проверку кор-
ней подстановкой в исходное уравнение. Первый корень не подходит.
Приходим к ответу:
4.
x
=
Пример 2. Решить уравнение
333
2325.
xxx
-+-=-
Решение. Возведем обе части уравнения в куб:
( ) ( )
( )
22
33
33
3
232(3)3(2)3325,
3(2)(3)230.
xxxxxxx
xxxx
-+×-×-+×-×-+-=-
×-×--+-=
Воспользовавшись исходным уравнением, заменим выражение
33
23
xx
-+-
выражением
3
25.
x
-
Получаем:
3
3
(2)(3)250.
xxx
-×-×-=
Решаем совокупность уравнений
2,
(2)(3)0,
3,
250;
2,5.
x
xx
x
x
x
=
é
-×-=
é
ê
=
ê
ê
-=
ë
ê
+
ë
В результате замены выражения могут появиться посторонние
корни, так как такое преобразование не является равносильным. По-
этому необходимо произвести проверку. Подставляем найденные зна-
чения и убеждаемся, что они являются корнями исходного уравнения.
Приходим к ответу:
123
2;2,5;3.
xxx
===
Пример 3. Решить уравнение
22
3432436.
xxxx++×+-=
Решение. Возведение уравнения в квадрат приводит к уравнению
четвертой степени и громоздкому решению.
Нетрудно заметить, что в данном уравнении можно произвести
замену. Но перед этим преобразуем уравнение следующим образом:
( )
22
22
324432424360,
3244324120.
xxxx
xxxx
+-++-+-=
+-++--=
Заменив
2
324,
xxy
+-=
получаем квадратное уравнение
2
4120.
yy
+-=
Решая его, находим корни
12
6,2.
yy
=-=
Возвращаемся к исходной неизвестной:
2
2
3246,
3242.
xx
xx
é
+-=-
ê
ê
+-=
ë
Первое уравнение решений не имеет, так как его левая часть неот-
рицательна, а правая – отрицательна. Второе уравнение возводим в
квадрат. Получаем:
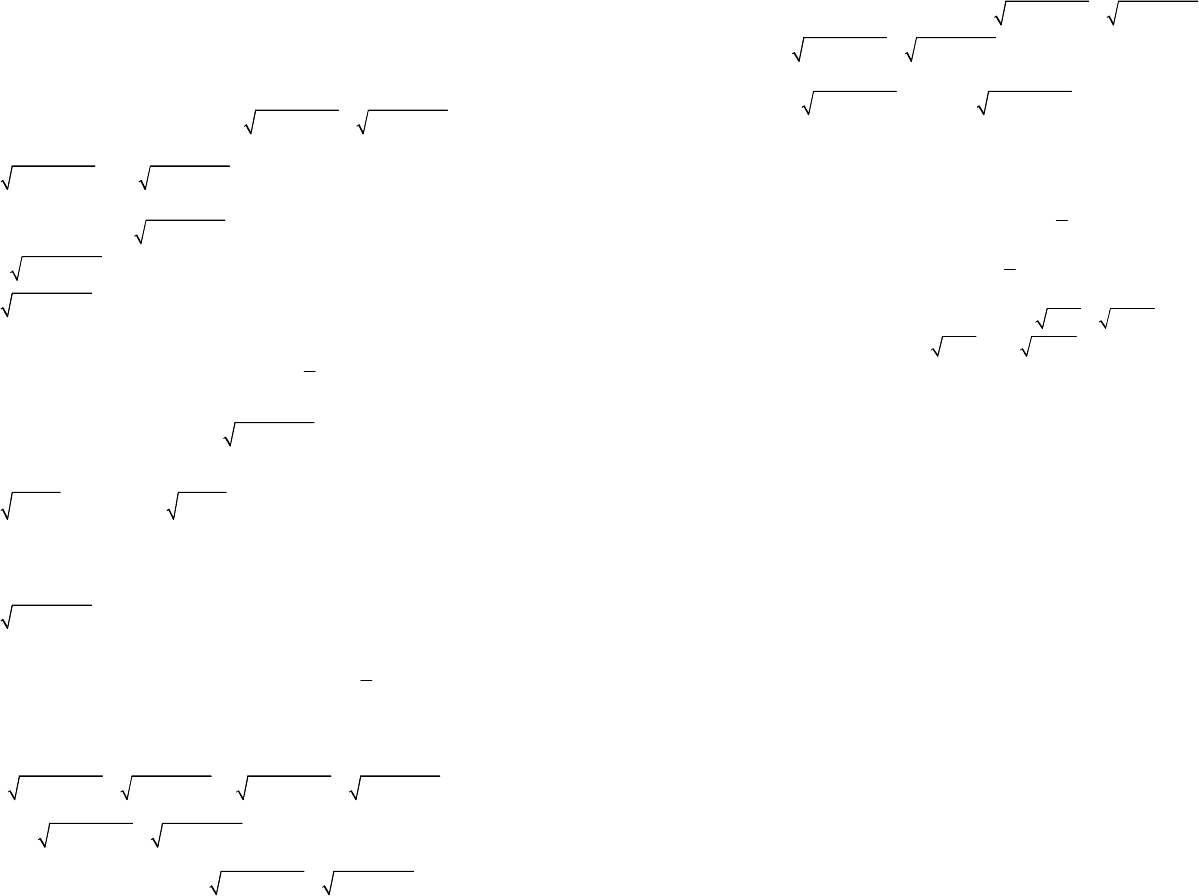
164 165
2
3244,
xx
+-=
т. е.
2
3280.
xx
+-=
Его корни
12
7,4.
xx
=-=
С помощью проверки убеждаемся, что
оба корня подходят, т. е. приходим к ответу:
12
7,4.
xx
=-=
Пример 4. Решить уравнение
22
26211.
xxxx
++-+-=
Решение. 1-й способ. Перенесем второй корень вправо:
22
26121.
xxxx
++=++-
Возводим обе части в квадрат:
222
2
2
26122121,
2216,
213.
xxxxxx
xx
xx
++=++-++-
+-=
+-=
Еще раз возводим в квадрат и получаем квадратное уравнение,
решая которое и получаем корни
12
5
,2.
2
xx
=-=
Делаем проверку
корней подстановкой в исходное уравнение. Оба корня подходят.
2-й способ. Введем замену
2
21,
xxy
+-=
тогда
22
21,
xxy
+-=
22
267.
xxy
++=+
Таким образом получили более простое уравнение
2
71,
yy
+-=
т. е.
2
71.
yy
+=+
Возведем его в квадрат:
22
712,260,2(3)0,3.
yyyyyy
+=++-=-==
Возвращаемся к исходной неизвестной:
2
213.
xx
+-=
Возводим обе части уравнения в квадрат:
22
219,2100,
xxxx
+-=+-=
откуда
12
5
,2.
2
xx
=-=
При помощи проверки убеждаемся, что оба корня подходят.
3-й способ. Домножим обе части уравнения на выражение, сопря-
женное левой части исходного уравнения. Получим:
(
)
(
)
( )
2222
22
26212621
12621,
xxxxxxxx
xxxx
++-+-×++++-=
=×++++-
2222
26(21)2621,
xxxxxxxx
++-+-=++++-
2222
22
2621)2621,
26217.
xxxxxxxx
xxxx
++--+=++++-
++++-=
Сложим последнее уравнение с исходным. Получим:
2
2268,
xx
++=
т. е.
2
264.
xx
++=
Последнее уравнение возводим в квадрат. Получаем квадратное
уравнение
22
2616,2100.
xxxx
++=+-=
Решая его, находим корни
12
5
,2.
2
xx
=-=
Приходим к ответу:
12
5
,2.
2
xx
=-=
Пример 5. Решить уравнение
44
1152.
xx
-++=
Решение. Пусть
44
1,15.
xaxb
-=+=
Тогда
44
1,15
xaxb
-=+=
и
44
11516,
abxx+=-++=
2
ab
+=
по условию.
Получили систему
44
16,
2.
ab
ab
ì
+=
ï
í
+=
ï
î
Решаем ее методом подстановки:
44
2,
16(2)0.
ba
aa
=-
ì
ï
í
-+-=
ï
î
Второе уравнение решим отдельно
224
(4)(4)(2)0;
aaa
-×++-=
(
)
23
(2)(2)(4)(2)0;
aaaa
-×+×++-=
(
)
32
(2)24160;
aaaa
-×-+=
(
)
2
2(2)2160.
aaaa
-×-+=
Получаем корни:
0,
2.
a
a
=
é
ê
=
ë
Возвращаемся к системе:
0,
2,
2.
a
a
ba
ì=
é
ï
ê
=
í
ë
ï
=-
î
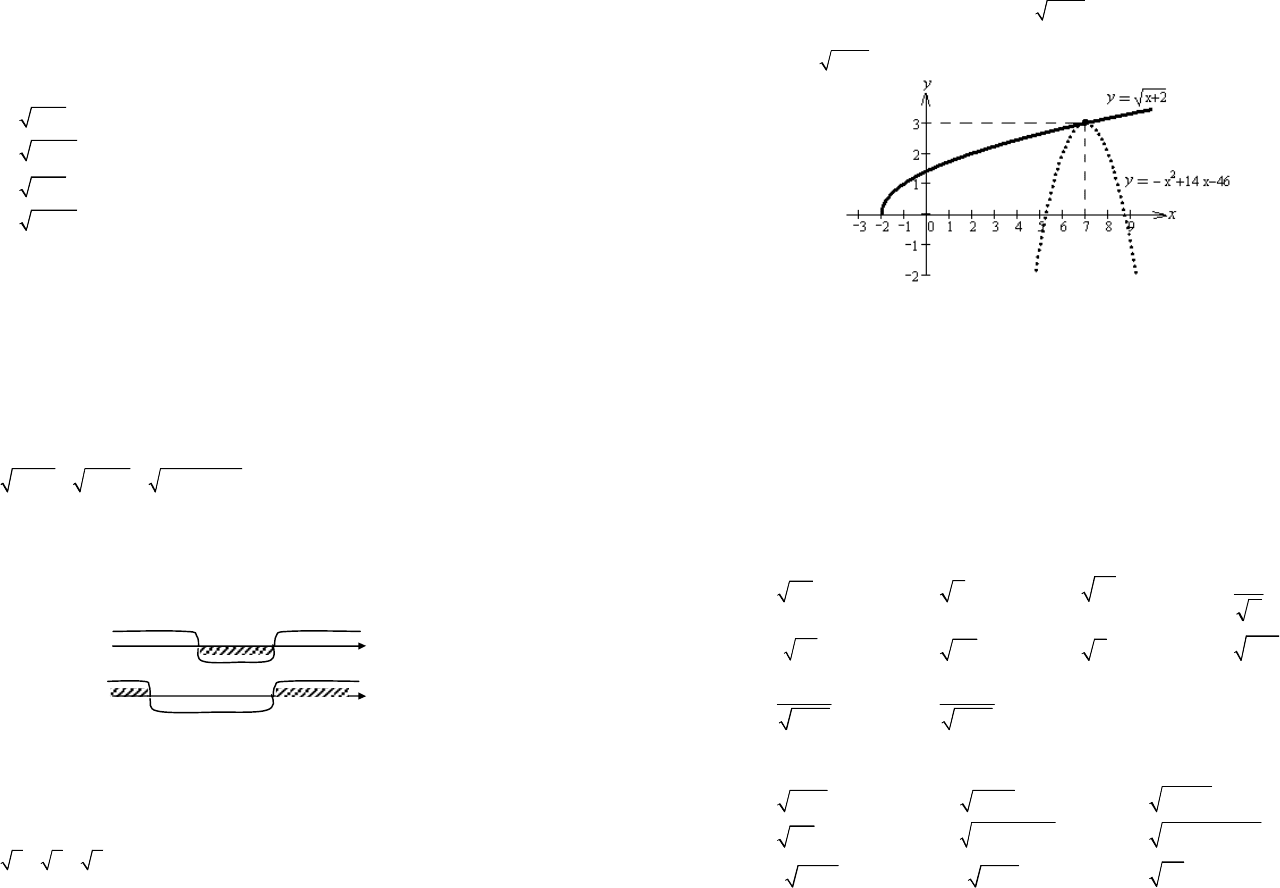
166 167
Получаем:
12
12
0,2,
2,0.
aa
bb
==
ì
í
==
î
Переходим к заданным неизвестным:
4
4
4
4
10,
152,
12,
150.
x
x
x
x
é
ì
-=
ï
ê
í
ê
+=
ï
î
ê
ì
ê
-=
ï
í
ê
+=
ï
ê
î
ë
Решая последнюю совокупность, находим корни
1
x
=
и
15.
x
=-
С помощью проверки убеждаемся, что оба корня подходят.
Получили ответ:
1,
x
=
15.
x
=-
При решении иррациональных уравнений, как правило, нахожде-
ние ОДЗ является бесполезным, так как проверка решений по ОДЗ не-
достаточна. Но существует ряд примеров, в которых нахождение ОДЗ
является тем методом, который приводит к успеху. Покажем это на
следующем примере.
Пример 6. Решить уравнение
222
182330.
xxxx
--+++-+=
Решение. Найдем ОДЗ данного уравнения:
22
22
10,10,
230;230;
xx
xxxx
ìì
-³-£
ïï
íí
+-³+-³
ïï
îî
(1)(1)0,
(1)(3)0.
xx
xx
-×+£
ì
í
-×+³
î
Решаем последнюю систему неравенств графически (рис. 5.10).
Рис. 5.10
Получили, что ОДЗ состоит из единственной точки
1.
x
=
Остается подставить значение
1
x
=
в уравнение и выяснить, явля-
ется ли оно решением:
09030.
-++=
Получили, что
1
x
=
– решение.
Пример 7. Решить уравнение
2
21446.
xxx+=-+-
Решение. Используем графический способ. Строим графики функ-
ций
2,
yx
=+
2
1446
yxx
=-+-
(рис. 5.11).
Рис. 5.11
Из рисунка видно, что графики пересекаются в единственной точ-
ке x = 7. Следовательно, уравнение имеет единственное решение. Про-
веряем x = 7 подстановкой в заданное уравнение и убеждаемся, что это
точное значение решения уравнения.
Получили ответ: x = 7.
Задания
I уровень
1.1. Определите, имеет ли уравнение корни:
1)
2;
x
-=
2)
3;
x
=-
3)
3
1;
x
=
4)
;5
1
=
x
5)
(
)
2
2;
x
-=
6)
3
3;
x
-=
7)
5
1;
x
=-
8)
4
2
2;
x
-=
9)
3
1
2;
1x
=-
+
10)
8
1
3.
1x
=-
+
1.2. Решите уравнение:
1)
12;
x
-=
2)
23;
x
-=
3)
2
31;
x
-=
4)
5;
x
-=
5)
2
524;
xx
++=
6)
23
320;
xx
--=
7)
(
)
2
33;
x
-=
8)
(
)
2
13;
x
+=
9)
2
5;
x
=
–
1
1
х
–
3
1
х
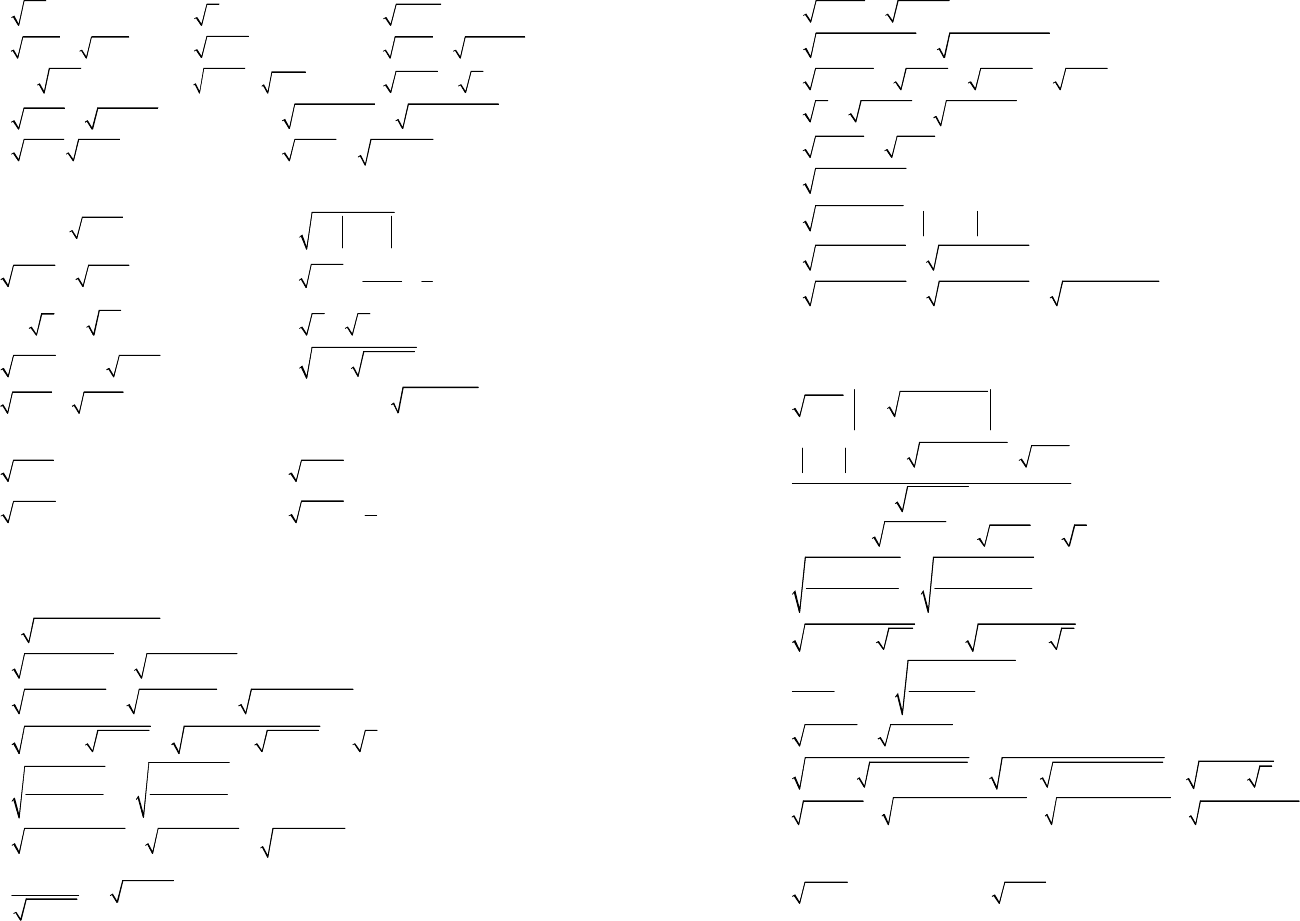
168 169
10)
4
2
2;
x
=
11)
3
2;
x
=-
12)
3
276;
x
-=
13)
35;
xx
-=+
14)
3
210;
x
+-=
15)
33
362;
xx
-=--
16)
5
2
32;
x
--=
17)
2
420;
xx
++-=
18)
33
60;
xx
++=
19)
52100;
xx
---=
20)
84
22
6560;
xxxx
--+-+=
21)
321;
xx
--=
22)
4
4
72(1).
xx
-=-
1.3. Решите уравнение:
1)
2
(10)30;
xx
-+=
2)
2
512;
x
--=
3)
233;
xx
-++=
4)
2
11
;
33
x
x
-+=
+
5)
3
2
3
32;
xx
-= 6)
36
20;
xx
+-=
7)
226;
xx
+=+-
8)
2
103;
xx
+-=
9)
4
2220;
xx-=--
10)
22
9912.
xxxx-++-+=
1.4. Решите уравнение графически:
1)
32;
x
-=
2)
24;
xx
+=-
3)
3
42;
x
+=
4)
3
5
44.
3
xx
+=-
II уровень
2.1. Решите уравнение:
1)
22
81216164433;
xxxx+-+-=
2)
22
33363;
xxxx
-++-+=
3)
222
41229;
xxxxxx
+++++=++
4)
225232572;
xxxx-+-+++-=
5)
2
2
1
23;
1
xxx
x
xx
+-
+=
+-
6)
222
25322(1);
xxxxx
++---=-
7)
2
2323;
32
x
xx
x
+-=
-
8)
21321;
xxx
+++=+
9)
22
2352353;
xxxxx
+++-+=
10)
11329720;
xxxx
+---++-=
11)
33
3
2312(1);
xxx
+-=-
12)
33
2111;
xx
-+-=
13)
222
56960;
xxyxxy
-+++-=
14)
2
12340;
xxx
-+--=
15)
3232
23;
xxxxx
+-+++=
16)
2215
4556670.
xxxxxx
--+--+++=
III уровень
3.1. Решите уравнение:
1)
(
)
2
121240;
xxx
+--+-=
2)
(
)
2
2
56211
0;
36
xxxxx
x
-+--+-
=
-
3)
2
252525248;
xxxxx-+-+-+=
4)
299
22
234
0;
2435
xxxx
xxxx
+-++
+=
++++
5)
44444;
xxxx
-+-=---
6)
2
24
2(2)
;
24
xx
xx
--
+=+
7)
44
776298;
xx
++-=
8)
22
2621121315821392;
xxxx+----++=+
9)
4752
36
54
(2)(2)(3)(2)(1)(2)(6)2.
xxxxxxxxxx
-+-++-++++=
3.2. Решите уравнение:
1)
;
xax
-=
2)
3.
xa
+=

170 171
6. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
ВЫРАЖЕНИЯ
6.1. Показательная функция, гиперболические
функции
Показательной функцией называется функция
,
x
ay = где
.1,0
¹
>
aa
Основные свойства показательной функции
1. Область определения:
).;()(
¥
+
-¥
=
yD
2. Множество значений:
(
)
.;0)( ¥+=yE
3. Четность и нечетность: не обладает свойством четности.
4. Периодичность: непериодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства: функция положитель-
на для
(
)
.; ¥+¥-Îx
7. Наибольшее и наименьшее значения: наибольшего и наи-
меньшего значений функция не имеет.
8. Промежутки возрастания и убывания: если ,1
>
a функ-
ция возрастает для всех
(
)
;; ¥+¥-Îx если
01,
a
<<
– убывает
для
(
)
.; ¥+¥-Îx
9. Точки пересечения с осями координат: пересекает ось Оу
в точке ,1
=
y ось Ох не пересекает.
10. Асимптоты: прямая y = 0 (ось Ох) является горизон-
тальной асимптотой.
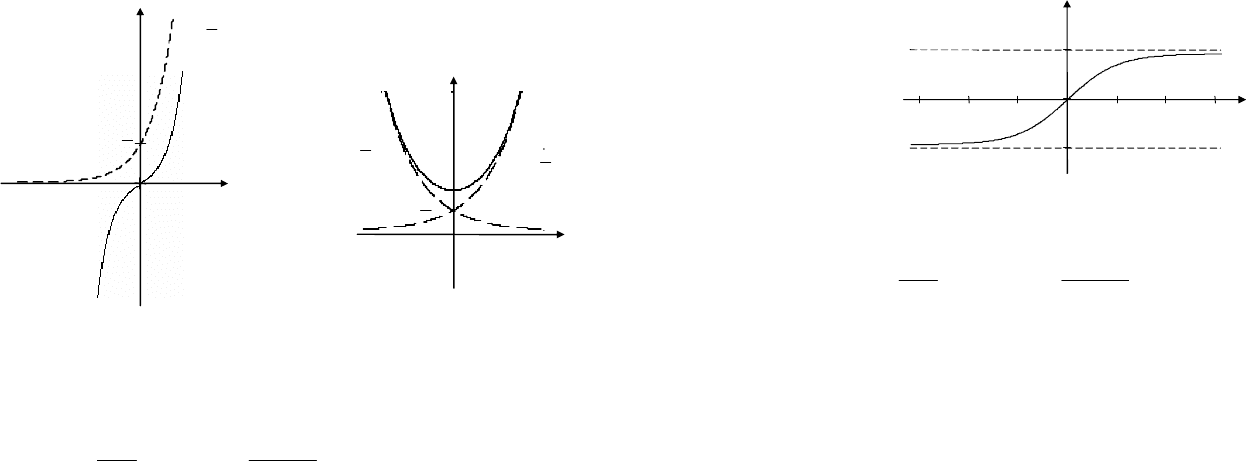
11. График функции для a > 1 изображен на рис. 6.1, для
10
<
<
a – на рис. 6.2.
Рис. 6.1 Рис. 6.2
Из свойств функции следует: неравенство
21
xx
aa > равно-
сильно неравенствам:
1) ,
21
xx > если ,1
>
a
2) ,
21
xx < если .10
<
<
a
Показательная функция с основанием е, где е – иррацио-
нальное число е = 2,718281…, называется экспонентой, пишут
x
ey = или
.
exp
x
y
=
Через показательные выражения с основанием е определя-
ются гиперболические функции.
Гиперболическим синусом называется функция
.
2
sh
xx
ee
x
-
-
=
Основные свойства гиперболического синуса
1. Область определения: ).;()(
¥
+
-¥
=
yD
2. Множество значений: ).;()(
¥
+
-¥
=
yE
3. Четность и нечетность: нечетная.
4. Периодичность: непериодическая.
5. Нули функции: .0
=
x
6. Промежутки знакопостоянства: функция отрицательна
для
(
)
,0;¥-Îx положительна – для
(
)
.;0 ¥+Îx
7. Наибольшее и наименьшее значения: наибольшего и наи-
меньшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрас-
тает для всех
(
)
.; ¥+¥-Îx
9. Точки пересечения с осями координат:
(
)
.0;0
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рис. 6.3.
Гиперболическим косинусом называется функция
.
2
сh
xx
ee
x
-
+
=
Основные свойства гиперболического косинуса
1. Область определения:
).;()(
¥
+
-¥
=
yD
2. Множество значений:
).;1[)(
¥
+
=
yE
3. Четность и нечетность: четная.
4. Периодичность: непериодическая.
у
у
х
х
1
0
0
у
=
а
х
,
a
>
1
у
=
а
х
,
0
<
a
<
1
1
172 173
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства: функция положитель-
на для
(
)
.; ¥+¥-Îx
7. Наибольшее и наименьшее значения: наименьшее значе-
ние, равное 1, функция принимает при .0
=
x
8. Промежутки возрастания и убывания: функция убывает
при
(
)
,0;¥-Îx возрастает при
(
)
.;0 ¥+Îx
9. Точки пересечения с осями координат: пересекает ось Оу
в точке ,1
=
y ось Ох не пересекает.
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рис. 6.4.
Рис. 6.3 Рис. 6.4
Гиперболические тангенс и котангенс определяются через
отношение гиперболических синуса и косинуса.
Гиперболическим тангенсом называется функция
,
ch
sh
th
x
x
x =
т. е. .th
xx
xx
ee
ee
x
-
-
+
-
=
Основные свойства гиперболического тангенса
1. Область определения:
).;()(
¥
+
-¥
=
yD
2. Множество значений:
).1;1()(
-
=
yE
3. Четность и нечетность: нечетная.
4. Периодичность: непериодическая.
5. Нули функции: .0
=
x
6. Промежутки знакопостоянства: функция отрицательна
для
(
)
,0;¥-Îx положительна для
(
)
.;0 ¥+Îx
7. Наибольшее и наименьшее значения: наибольшего и наи-
меньшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрас-
тает для
(
)
.; ¥+¥-Îx
9. Точки пересечения с осями координат:
(
)
.0;0
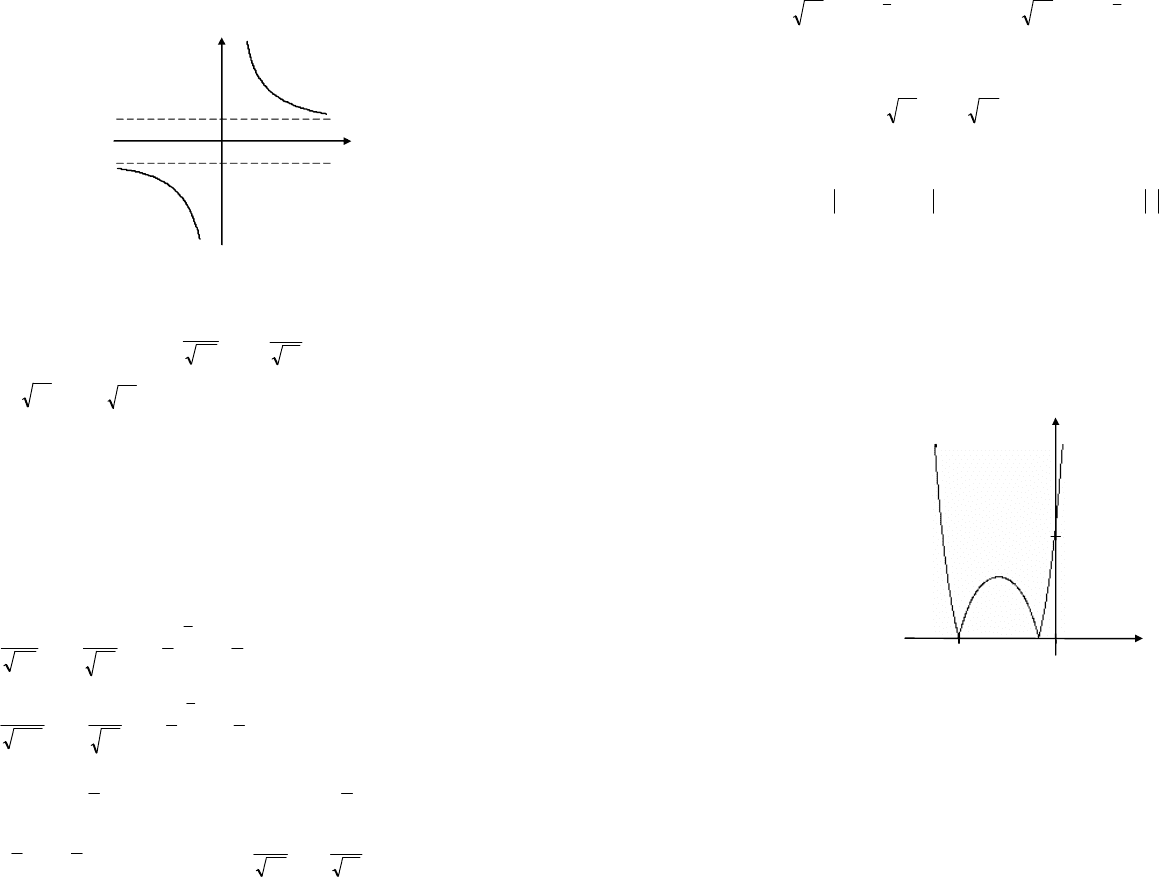
10. Асимптоты: имеет горизонтальные асимптоты
1
-
=
y
и
.1
=
y
11. График функции изображен на рис. 6.5.
Рис. 6.5
Гиперболический котангенсом называется функция
,
sh
ch
сth
x
x
x =
т. е. .сth
xx
xx
ee
ee
x
-
-
-
+
=
Основные свойства гиперболического котангенса
1. Область определения:
(
)
.;0)0;()( ¥+È-¥=yD
2. Множество значений:
(
)
.;1)1;()( ¥+È--¥=yE
3. Четность и нечетность: нечетная.
4. Периодичность: непериодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства: функция отрицательна
для
(
)
,0;¥-Îx
положительна для
(
)
.;0 ¥+Îx
7. Наибольшее и наименьшее значения: наибольшего и наи-
меньшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция убывает
для ).( yDx
Î
9. Точки пересечения с осями координат: нет.
0
х
у
у
=
ch
x
1
2
1
2
õ
óå
-
=
1
2
õ
óå
=
–
3
–
2
–
1
0
1
2
3
–
1
1
х
у
у = th x
0
1
2
х
y = sh x
1
2
õ
óå
=
174 175
10. Асимптоты: имеет горизонтальные асимптоты 1
-
=
y и
.1
=
y
11. График функции изображен на рис. 6.6.
Рис. 6.6
Пример 1. Сравнить числа:
1)
23
25 и ;125
12
2)
8
27
1
÷
÷
ø
ö
ç
ç
è
æ
и
;
81
1
5
÷
÷
ø
ö
ç
ç
è
æ
3)
10
5
3
÷
ø
ö
ç
è
æ
e
и
.
12
3
2
÷
ø
ö
ç
è
æ
e
Решение. 1) Преобразуем числа к одному основанию:
(
)
,5525
46
23
223
==
(
)
.55125
36
12
312
==
Так как
,15
>
3646
>
и функция
5
xy = монотонно возрастает, то
,55
3646
> следовательно, .12525
1223
>
2) Преобразуем числа:
;
3
1
3
1
3
1
27
1
128
2
3
8
3
8
÷
ø
ö
ç
è
æ
=
÷
ø
ö
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
×
.
3
1
3
1
3
1
243
1
156
2
5
6
5
6
÷
ø
ö
ç
è
æ
=
÷
ø
ö
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
×
Так как ,1
3
1
0 << 1512
<
и функция
x
y
÷
ø
ö
ç
è
æ
=
3
1
монотонно убыва-
ет, то
,
3
1
3
1
1512
÷
ø
ö
ç
è
æ
>
÷
ø
ö
ç
è
æ
следовательно,
.
81
1
27
1
58
÷
÷
ø
ö
ç
ç
è
æ
>
÷
÷
ø
ö
ç
ç
è
æ
3) Преобразуем числа:
,
6
10
5
3
10
5
3
eee =
÷
÷
ø
ö
ç
ç
è
æ
=
÷
ø
ö
ç
è
æ
.
8
12
3
2
12
3
2
eee =
÷
÷
ø
ö
ç
ç
è
æ
=
÷
ø
ö
ç
è
æ
Так как ,1
>
e 86
<
и функция
x
ey =
монотонно возрастает, то
,
86
ee < тогда и .
12
3
2
10
5
3
÷
ø
ö
ç
è
æ
<
÷
ø
ö
ç
è
æ
ee
Пример 2. Построить график функции:
1) ;4)3(ch -+= xy 2) .2th -= xy
Решение. 1) Строим график функции .ch xy
=
График функции 4)3(ch
-
+
=
xy получаем из предыдущего пу-
тем смещения его на 3 единицы влево по оси Ох и на 4 единицы вниз
по оси Оу.
Для построения графика заданной функции оставляем ту часть гра-
фика функции ,4)3(ch
-
+
=
xy которая лежит над осью Ох и на оси Ох.
Ту часть графика, которая расположена ниже оси Ох, отображаем в
верхнюю полуплоскость симметрично относительно оси Ох (рис. 6.7).
Рис. 6.7
2) Строим график функции
th
yx
=
(см. рис. 6.5).
График функции 2th
-
=
xy получаем из предыдущего путем
смещения его на 2 единицы вниз вдоль оси Оу.
Для построения графика заданной функции оставляем ту часть
графика функции ,2th
-
=
xy которая лежит правее оси Оу и на оси
Оу. Часть графика, которая лежит левее оси Оу, отбрасываем, а остав-
шуюся часть отображаем в левую полуплоскость симметрично оси Оу
(рис. 6.8).
у
0
х
–
1
у = cth x
1
–
5
0
5
у
х
