Майсеня Л.И. Математика в примерах и задачах. Часть 1
Подождите немного. Документ загружается.

136 137
Решение системы – пересечение двух указанных областей (на
рис. 4.24 показано наложением двух штриховок).
Задания
I уровень
1.1. Решите графически:
1) ;4
22
³+ yx 2)
;05
<
-
+
yx
3) ;
2
xy > 4) ;254
22
£+< yx
5)
î
í
ì
³
£+
;0
,1
y
yx
6)
î
í
ì
£+-
>+-
;012
,032
xy
xy
7)
î
í
ì
=
£++-
;
,16)3()1(
2
22
xy
yx
8)
î
í
ì
-<
+³
.2
,1
2
xy
xy
II уровень
2.1. Решите графически:
1)
(
)
(
)
ï
î
ï
í
ì
<-+
£++-
;02
,1642
22
xy
yx
2)
î
í
ì
-³
-£
;1
,2
yx
xy
3)
ï
î
ï
í
ì
³-
+
<
.02
,
2
1
y
x
y
2.2. Найдите количество целочисленных решений системы:
1)
î
í
ì
>
£
;
,4
3
xy
xy
2)
î
í
ì
³-
£-
;02
,
2
yx
yx
3)
( )
ï
ï
î
ï
ï
í
ì
³-
³--
<++-
.4
,01
,12
2
2
2
yx
yx
yxx
2.3. Найдите все целочисленные решения системы:
1)
( ) ( )
ï
î
ï
í
ì
-=
>+
£-+-
;
,4
,2522
22
22
yx
yx
yx
2)
ï
ï
î
ï
ï
í
ì
£+-
>
£
>+-
;02
,0
,0
,07
2
x
y
x
xy
3)
ï
î
ï
í
ì
>-+
³
.05
,0
1
22
yx
x
2.4. Решите неравенство. В ответе укажите количество ре-
шений с двумя целочисленными координатами:
.0)(4
22
£--+ yxyx
III уровень
3.1. Найдите количество целочисленных решений системы:
1)
( )
2
,
240;
xyxy
yx
ì-=-
ï
í
+-<
ï
î
2)
22
2
16,
.
xy
yx
ì
+£
ï
í
³
ï
î
3.2. Найдите все значения параметра а, при каждом из кото-
рых система имеет решение:
1)
î
í
ì
=
<-+
;
,54
2
22
axy
yyx
2)
(
)
î
í
ì
=+
<++-+
.25
,0252
22
22
ax
xaxax
3.3. Определите, при каких значениях а неравенство
(
)
2
14 ++-> xax имеет положительные решения.
3.4. Определите, при каких значениях а система имеет един-
ственное решение:
1)
ï
î
ï
í
ì
£-
+-³+
+³-
;43
,52
,1235
axy
ayx
axy
2)
î
í
ì
³
£+
;
,243
ay
yx
3)
î
í
ì
³
£+
.
,62
bx
yx
3.5. В зависимости от значения а определите число решений
системы
( )
ï
î
ï
í
ì
£+
+³
+³
.4
,3
,3
22
yxa
yay
yax
3.6. Решите графически:
1)
(
)
(
)
;038 ³+×- yx
2) .09
22
<- yx
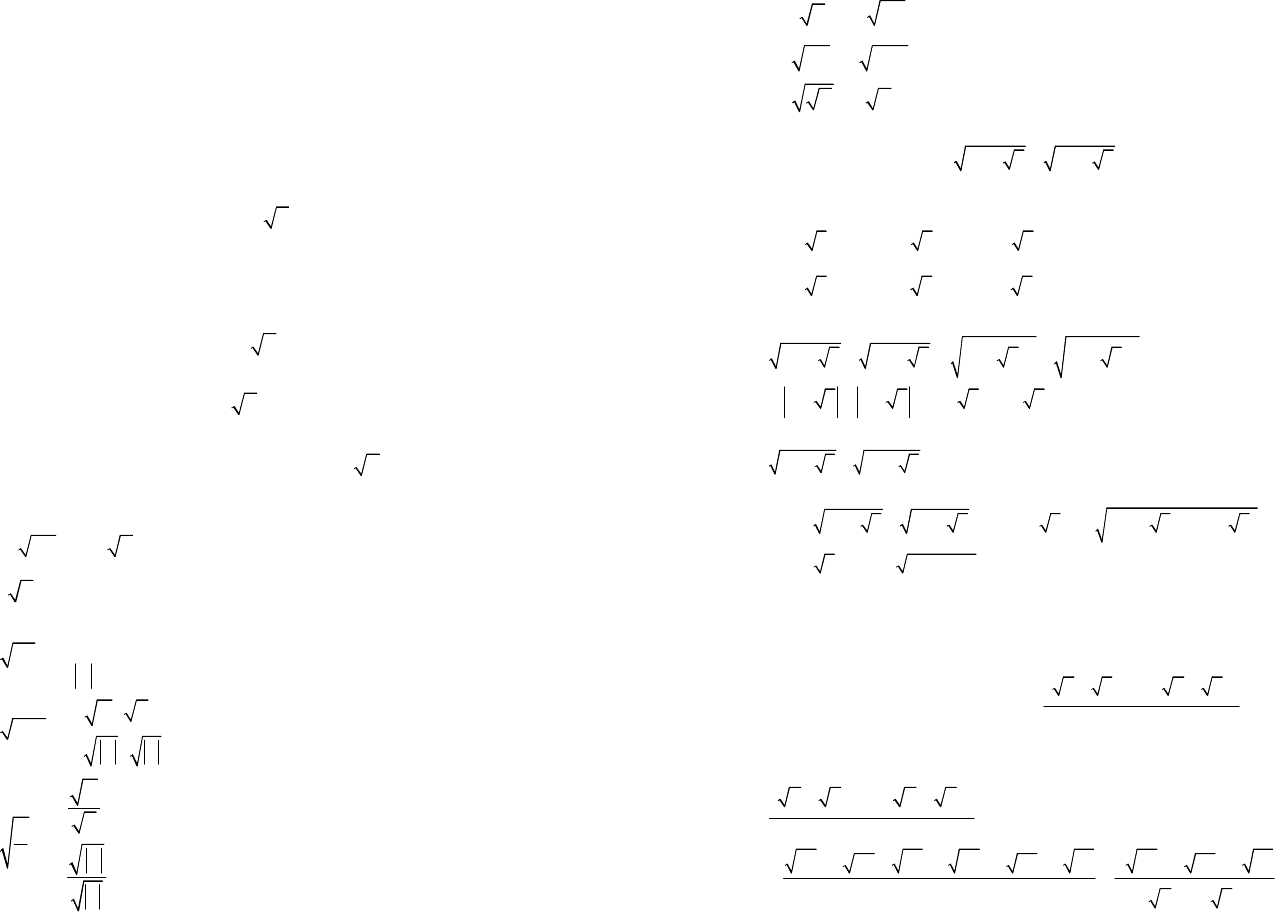
138 139
5. СТЕПЕНИ И КОРНИ
5.1. Корень n-й степени
Для всякого числа a Î R определена степень с натуральным
показателем a
n
, n Î N.
Число b Î R называется корнем n-й степени, n Î N, n ³ 2,
из числа а, если
,
n
ba
=
обозначают
.
n
a
Нахождение корня n-й степени из данного числа а называют
извлечением корня n-й степени из числа а. Число а, из которо-
го извлекается корень n-й степени, называют подкоренным вы-
ражением, а число n – показателем корня.
Если
(
)
21, ,
nkk=+Î
N
то
21k
a
+
определен для всех a Î R
и принимает любые действительные значения.
Если
(
)
2, ,
nkk=Î
N
то
2k
a
определен для всех a ³ 0
(a Î R). В курсе элементарной математики рассматривают
арифметическое значение корня, т. е. число
2
0.
k
a
³
Свойства корней
Пусть a, b Î R, тогда:
1)
2121
;
kk
aa
++
-=-
2)
( )
, åñëè 21,
0, åñëè 2;
n
n
ank
a
ank
=+
ì
=
í
³=
î
3)
, åñëè 21,
, åñëè 2;
n
n
ank
a
ank
=+
ì
ï
=
í
=
ï
î
4)
, åñëè 21,
, åñëè 2,0;
n
n
n
nn
abnk
ab
abnkab
ì
×=+
ï
×=
í
×=׳
ï
î
5)
, åñëè 21,0,
, åñëè 2,0,0;
n
n
n
n
n
a
nkb
b
a
a
b
nkabb
b
ì
=+¹
ï
ï
=
í
ï
=׳¹
ï
î
6)
(
)
,,
m
n
m
n
aam
=Î
R
где a ³ 0 в случае
2;
nk
=
7)
,,
nnk
mmk
aak
×
×
=Î
N
где
0
m
a
³
в случае
2;
nk
=
8)
,
m
nmn
aa
×
= где
0
a
³
в случае
2.
nk
=
Пример 1. Вычислить
743743.
++-
Решение. 1-й способ. Выделим полные квадраты подкоренных
выражений:
(
)
2
7434223323;
+=+××+=+
(
)
2
7434223323.
-=-××+=-
Тогда получим
( ) ( )
22
7437432323
232323234.
++-=++-=
=++-=++-=
2-й способ. Обозначим вычисляемое выражение через a, т. е.
743743.
a
++-=
Заметим, что
0.
a
>
Возведем обе части полученного равенства в квадрат:
(
)
( ) ( )
2
2
7437437432743743
7431424916314216.
a
=++-=++×+×-+
+-=+-×=+=
Тогда
4.
a
=±
Поскольку исходное выражение положительно, в ответе получаем
a = 4.
Пример 2. Упростить выражение
( ) ( )
22
3333
3
.
abab
ab
-++
-
Решение. 1-й способ. Используем формулы квадрата разности и
суммы, а также свойства корней. Получаем:
(
)
(
)
22
3333
3abab
ab
-++
=
-
( ) ( )
333333
222222
333
33
33
2363444aabbaabbaabb
ab
ab
-++++++
===
-
-
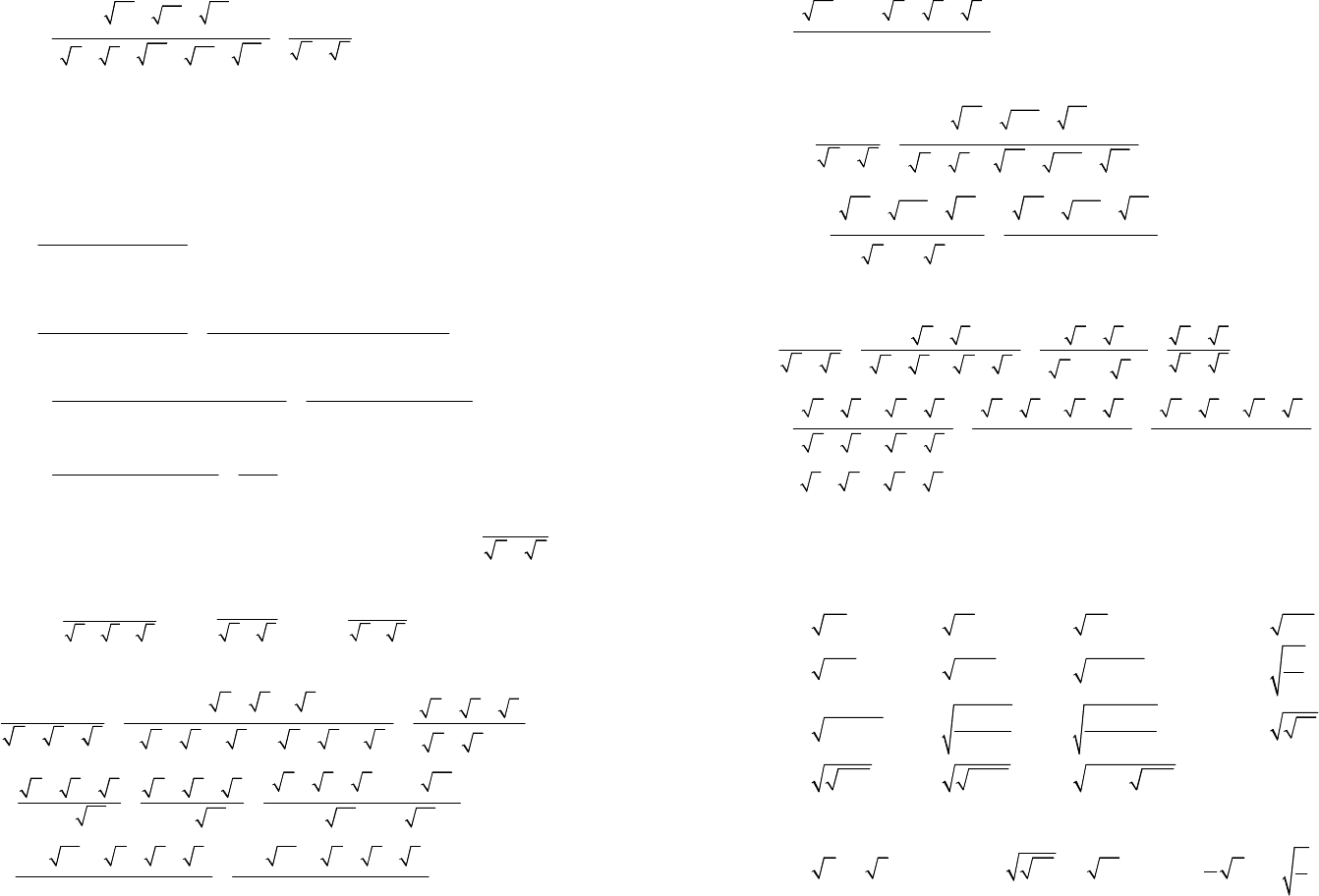
140 141
(
)
( )
(
)
33
22
3
33
33
22
333
4
4
.
aabb
ab
abaabb
++
==
-
-++
2-й способ. При упрощении иррациональных выражений часто
бывает эффективным метод рационализации, основанный на замене
переменных.
Введем такую замену переменных, чтобы корни извлеклись:
33
,.
axby
==
Заданное выражение приобретает вид
( ) ( )
22
33
3
.
xyxy
xy
-++
-
Упрощаем его, используя формулы сокращенного умножения:
( ) ( )
(
)
( )
( )
( )
( )
( )
( )
2222
22
33
22
222222
2222
232
3
2363444
xxyyxxyy
xyxy
xy
xyxxyy
xxyyxxyyxxyy
xyxxyyxyxxyy
-++++
-++
==
-
-×++
-++++++
===
-×++-×++
(
)
( )
( )
22
22
4
4
.
xxyy
xy
xyxxyy
++
==
-
-×++
Возвращаясь к старым переменным, приходим к ответу
33
4
.
ab
-
Пример 3. Избавиться от иррациональности в знаменателе:
1)
1
;
753
++
2)
33
1
;
73
+
3)
4 4
1
.
23
+
Решение. 1) Умножим числитель и знаменатель дважды на сопря-
женные выражения и воспользуемся формулой разности квадратов:
(
)
( )
( )
( )
( )
( )
2
753
1753
753
753753
753
+-
+-
===
++
++×+-
+-
( )
(
)
(
)
( ) ( )
753535
753753
10235
25352535535
+-×-
+-+-
====
+
++×-
(
)
(
)
( )
(
)
(
)
535753535753
2253520
-×+--×+-
===
--
(
)
(
)
355753
.
20
-×+-
=
2) Домножим числитель и знаменатель на неполный квадрат раз-
ности и воспользуемся формулой суммы кубов:
(
)
( )
( )
33
22
3
33
33
22
333
7733
1
73
737733
-×+
==
+
+×-×+
(
)
( ) ( )
(
)
3333
2222
33
33
33
77337733
.
10
73
-×+-×+
==
+
3) Умножим числитель и знаменатель дважды на сопряженные
выражения:
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( ) ( ) ( )
( ) ( )
444444
22
44
44
44
4
4
444
444
44
1232323
2323
2323
23
232323232323
231
2323
3223.
---
====
+-
+×-
-
-×+-×+-×+
====
--
-×+
=-×+
Задания
I уровень
1.1. Вычислите значения корней:
1)
3
8;
-
2)
4
81;
3)
6
64;
4)
5
243;
5)
3
216;
6)
4
2401;
7)
3
0,125;
- 8)
4
1
;
81
9)
3
0,343;
-
10)
3
27125
;
8
×
11)
4
81
;
6252401
×
12)
16;
13)
3
729;
14)
5
1024;
15)
3
64729.
-×
1.2. Сравните числа:
1)
4
4
и
3
3;
2)
4
5
99
и
10
10;
3)
3
1
2
2
и
2
6
1
;
2
æö
ç÷
ç÷
èø
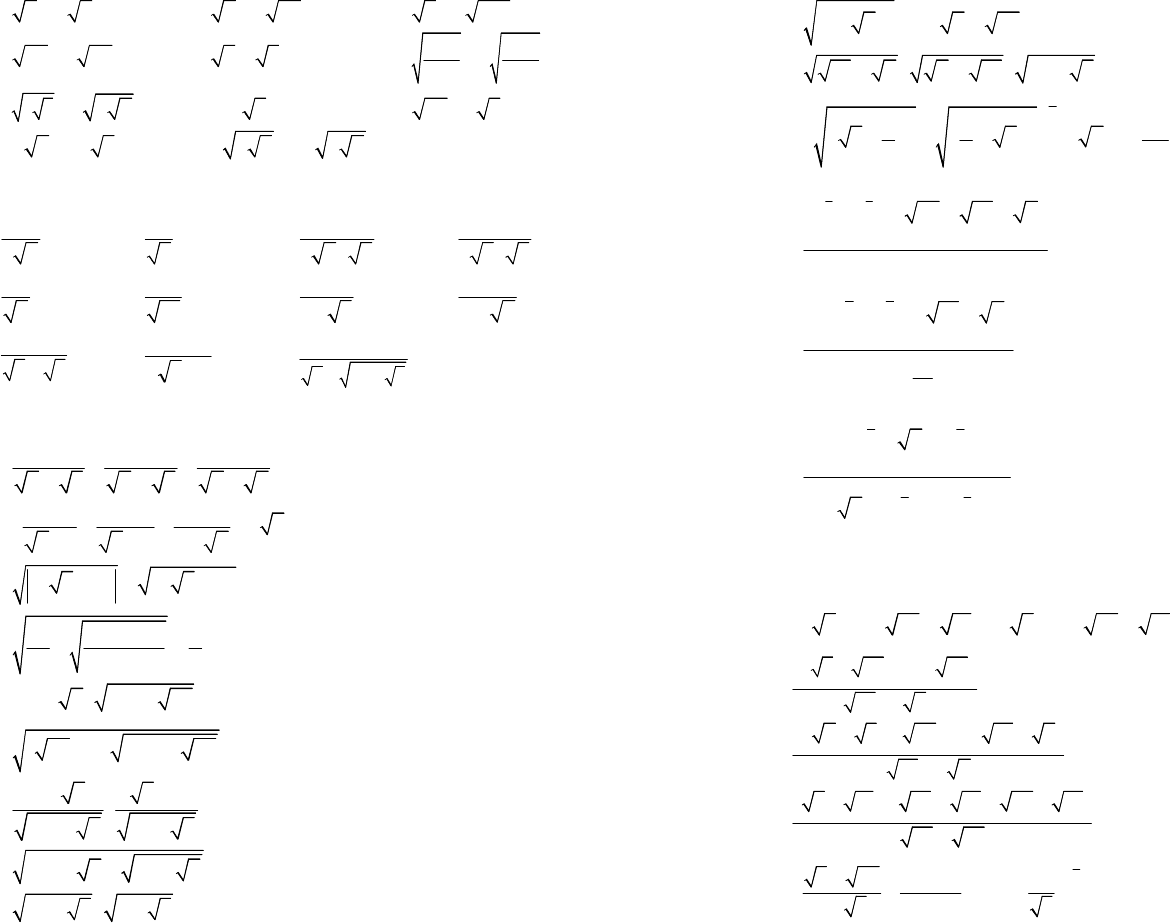
142 143
4)
2
и
61;
-
5)
3
7
и
6
40;
6)
5
и
8
500;
7)
5
5
-
и
3
3;
-
8)
3
63
- и 1; 9)
5
1990
1992
и
5
1989
;
1991
10)
53
и
62;
11) 3 и
5;
12)
4
26
и
5;
13)
4
4
- и
3
3;
- 14)
3
26
- и
3
52.
-
1.3. Избавьтесь от иррациональности в знаменателе:
1)
1
;
52
2)
3
1
;
3
3)
2
;
325
×
4)
3
1
;
333
×
5)
4
3
;
9
6)
6
1
;
16
-
7)
4
;
15
+
8)
2
;
22
-
9)
1
;
53
-
10) ;
532
1
+
11)
2
.
2323
-+
1.4. Упростите выражение:
1)
341
0;
637376
+-=
-+-
2)
( )
15412
611115;
616236
æö
+-×+=-
ç÷
+--
èø
3)
12529125296;
--+=-
4)
3
22
2353
;
644
4832
+=
-
5)
(
)
532435727;
-+=
6)
( )
9741138972;
+-=
7)
4552
1;
2185945
+-
×=
+-
8)
4
62667265;
+-+=
9)
63
743231;
+×-=
10)
( ) ( )
6
333
6
1616365;
-×++=
11)
333
44
1222122232;
+×-×+=-
12)
1
2
23
3
557
552sin2;
224
p
æö
æöæö
ç÷
----×=
ç÷ç÷
ç÷
èøèø
èø
13)
( )
11
333
33
5225104
28;
0,25
æö
+×-+
ç÷
ç÷
èø
=
14)
( )
11
22
3157157
6,5;
9
3
13
æö
-×+
ç÷
ç÷
èø
=
æö
+
ç÷
èø
15)
11
22
1
1
32
3272
0,2.
32616641
æö
-
ç÷
ç÷
èø
=
æöæö
-×+
ç÷ç÷
ç÷ç÷
èøèø
II уровень
2.1. Упростите выражение:
1)
(
)
(
)
4545511454551120;
--+×+++=
2)
(
)
(
)
5350524
1;
7552
+×-
=
-
3)
(
)
(
)
223243166
2,5;
1222
-×+++
=
+
4)
(
)
(
)
51133152210
1,2;
7550
-×+--
=-
-
5)
1
2
0,5
44
2
0,25
327136
4;
3
333
-
-
-
æö
-+
æö
+×-
ç÷
ç÷
ç÷
-
èø
èø
144 145
6)
2
642642
8;
26422642
æö
+-
+=
ç÷
ç÷
++--
èø
7)
( ) ( )
62
32
3
25
25251;
25
--
æöæö
×-+×-=-
ç÷ç÷
ç÷ç÷
-
èøèø
8)
22232223223231;
-++×+++×++×+=
9)
334122278423.
---+-
2.2. Избавьтесь от иррациональности в знаменателе:
1)
3
1
;
12
+
2)
3
1
;
41
-
3)
3
3
2
;
23
-
4)
33
2
;
42
+
5)
156
;
3514
-
-
6)
2
;
232
+
7)
323
;
323
+
-
8)
1
;
123
++
9)
1
;
532
-+
10)
1
;
532
--
11)
3
1
;
23
-
12)
4
1
.
23
+
2.3. Упростите выражение:
1)
(
)
(
)
3
33
22
2
333
:1
1
;
aabbab
a
b
abb
æö
++-
ç÷
-=
ç÷
-
ç÷
èø
2)
( ) ( )
3
2
3
22
33333
3
3;
aaa
babab
aa
æö
-
æö
ç÷
-×-++
ç÷
ç÷
èø
+
èø
3)
1
11
22
2112
3
3
3333
2
:;
xyxy
xy
xy
xxyy
-
æö
+-
+
ç÷
ç÷
+
ç÷
-×+
èø
4)
2
33
44
4
1
12.
xyxyxy
xx
yy
xyxy
-
æö
-+
ç÷
+×++
ç÷
-
èø
III уровень
3.1. Избавьтесь от иррациональности в знаменателе:
1)
3
33
1
;
469
++
2)
333
1
;
162025
-+
3)
88
1
;
53
+
4)
1
;
2357
+++
5)
;
117532
1
--+-
6)
5
2
;
31
-
7)
444
2
;
2481
+--
8)
444
2
;
3927
++
9)
88
1
;
75
-
10)
1
;
5237
+-+
11)
44
1
;
35
+
12)
44
1
;
75
-
13)
33333
1
.
39131525
-+-+
3.2. Упростите выражение:
1)
33
20142201424;
++-=
2)
837837
;
3535
++-
+--
3)
3
31953
;
31953
--
-
++
4)
3
211072
;
211072
-+
×
+-
5)
(
)
(
)
( ) ( )
33
2
33
20164554
;
275423
-×+
---
6)
882040;
+++
7)
4
44
821
;
821821
-+
+----
8)
62
23;
22
+--
9)
821025821025;
+++-+
10)
1111
....
12233499100
++++
++++

146 147
5.2. Степень с произвольным действительным
показателем
Во множестве R определена степень a
x
с действительным
показателем.
В выражении a
x
число а называют основанием степени,
число x – показателем степени. Нахождение значения степени
называют возведением в степень.
Степень с действительным показателем
Пусть a Î R, тогда:
1)
...,
n
n ðàç
aaaa
=×××
14243
n Î N;
2)
0
1,0;
aa
=¹
3)
1
,,0;
n
n
ana
a
-
=ι
N
4)
1
,,2
n
n
aann
=γ
N и a ³ 0, если
2, ;
nkk
=Î
N
5)
( )
, , 2,
m
m
n
n
aannm
=γÎ
NN
и если
2, ,
nkk
=Î
N
то a ³ 0;
6)
1
, 0,,2,
m
n
m
n
aannm
a
-
=¹Î³Î
NN
и если
2, ,
nkk
=Î
N
0;
a
>
7)
,
k
a
где
,
k
Î
I
определяется следующим образом.
Пусть иррациональное число k записано в виде десятичной
дроби,
()
n
uk
– последовательность его десятичных приближе-
ний с недостатком (или с избытком). Для любого действитель-
ного числа а > 0 степень
k
a
с иррациональным показателем оп-
ределяется равенством
lim.
n
k
k
n
aa
®¥
=
На множестве R не определены отрицательная и нулевая
степень числа 0, а также
1
,
n
a
если
0
a
<
2, .
nkk
=Î
N
Свойства степеней
Допустим, что a, b, c Î R и это такие числа, что все степени
имеют смысл. Тогда:
1)
;
bcbc
aaa
+
×=
2)
;
b
bc
c
a
a
a
-
=
3)
(
)
;
c
bbc
aa
=
4)
( )
;
c
cc
abab
×=×
5)
;
c
c
c
aa
b
b
æö
=
ç÷
èø
6) если a > 1 и x < y, то
,
xy
aa
<
если 0 < a < 1 и x < y, то
;
xy
aa
>
7) если 0 < a < b и x >0, то
,
xx
ab
<
если 0 < a < b и x < 0, то
.
xx
ab
>
Пример 1. Вычислить
( )
( )
6
380
3
609
232
.
82256
eeee
eee
×-×
×+×
Решение. Используем свойства степеней
( )
( )
( )
( )
( )
6
380
6635866358
3363679
609
23679
58
6958
697969
232
22122
22
82128
212
221
2221
.
6
22212
eeee
eeeee
ee
eee
eee
ee
eee
e
eee
+
+
×-×
××-×××-×
===
×+×
×+××
××+××
×-
×-×-
===
×+××+
Пришли к ответу:
21
.
6
e
e
-
Задания
I уровень
1.1. Представьте выражение в виде степени с рациональным
показателем:
1)
34
555;
× 2)
(
)
2
5
3:3;
3)
2
55;
4)
2
6
333;
æö
ç÷
èø
148 149
5)
1
6
3
3
3
422;
æö
ç÷
èø
6)
4
35
3
1256255:5;
7)
3
39273;
8)
4
8
222;
9) ;27:243:729
4
3
10) ;625125255
5
5
5
5
11) ;
3
3
x
y
x
y
y
x
y
x
× 12) ;:
2
6
3
4
42
÷
÷
ø
ö
ç
ç
è
æ
÷
ø
ö
ç
è
æ
x
y
y
x
yx
x
y
13) ;
4
22
yxxy 14)
36
25
.
aaaa
-
××
1.2. Выполните действия:
1)
83
410
(2)5
;
5210
-×
××
2)
( )
7
5
10
20,75;
27
-
æö
×
ç÷
èø
3)
20
1015
42
;
216
×
4)
33
3
22
;
41
-
+
+
5)
( )
(
)
3
3
2
16:4;
-
-
- 6)
1
1223
2
3354
2783281;
æö
×××
ç÷
ç÷
èø
7)
201
2
353
4:;
462
-
-
æöæö
æöæöæö
-+
ç÷ç÷
ç÷ç÷ç÷
ç÷ç÷
èøèøèø
èøèø
8)
2
8
0
1
4
3
3;
2
-
-
æö
æö
æö
ç÷
+
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
9)
542
2
111
64
18276
.
2
3
--
-
æöæöæö
××+
ç÷ç÷ç÷
èøèøèø
æö
ç÷
èø
1.3. Найдите
x
из уравнения:
1)
0,2
2;
x = 2)
3
27;
xx= 3)
3,2
3
77;
x
-
=
4)
3
2
27;
x = 5)
0,4
3
9;
x
-
= 6)
3.
xx=
1.4. Упростите выражение
111131
222222
1111
2222
2
.
xyxyxyy
xyxy
xyxyxyxy
æö
-+
ç÷
+×-
ç÷
+-
ç÷
+-
èø
II уровень
2.1. Вычислите:
1)
( )
42
22
234117
;
2344681
--
--
-
-
2)
( )
0,751,25
0,250,25
70,25
70,25:;
47
-
æö
--
ç÷
èø
3)
( )
( ) ( )
1
1
0,50,50,5
350,251555;
-
-
-æö
-+×+-
ç÷
èø
4)
(
)
( )
2
3
432
202122482:8;
×-×-×-
5)
3018121830
2412624624
75357
;
323315521
-
×-××
×-×+×
6)
22
21877292438127
.
3924318541629
×+××
××+×××
2.2. Упростите выражение:
1)
( ) ( )
( )
2
11
4444
:;
4
ab
abab
ab
-
--
-
æö
-++
ç÷
èø
+
2)
22
51115111
66336633
2
112211
333333
4
2;
babababa
a
a
ab
ababab
--
--
æöæö
++-
ç÷ç÷
ç÷ç÷
èøèø
-+
-
æöæö
-×++
ç÷ç÷
ç÷ç÷
èøèø
3)
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
11
1111
2222
11
1111
2222
.
kmkmkmkm
kmkmkmkm
--
----
--
----
æöæö
++-++--
ç÷ç÷
èøèø
æöæö
++--+--
ç÷ç÷
èøèø
III уровень
3.1. Вычислите:
1)
(
)
(
)
4589363718219135
62313232322;
-×-××+×+×+
2)
616
1281261271281291302;
-××××+
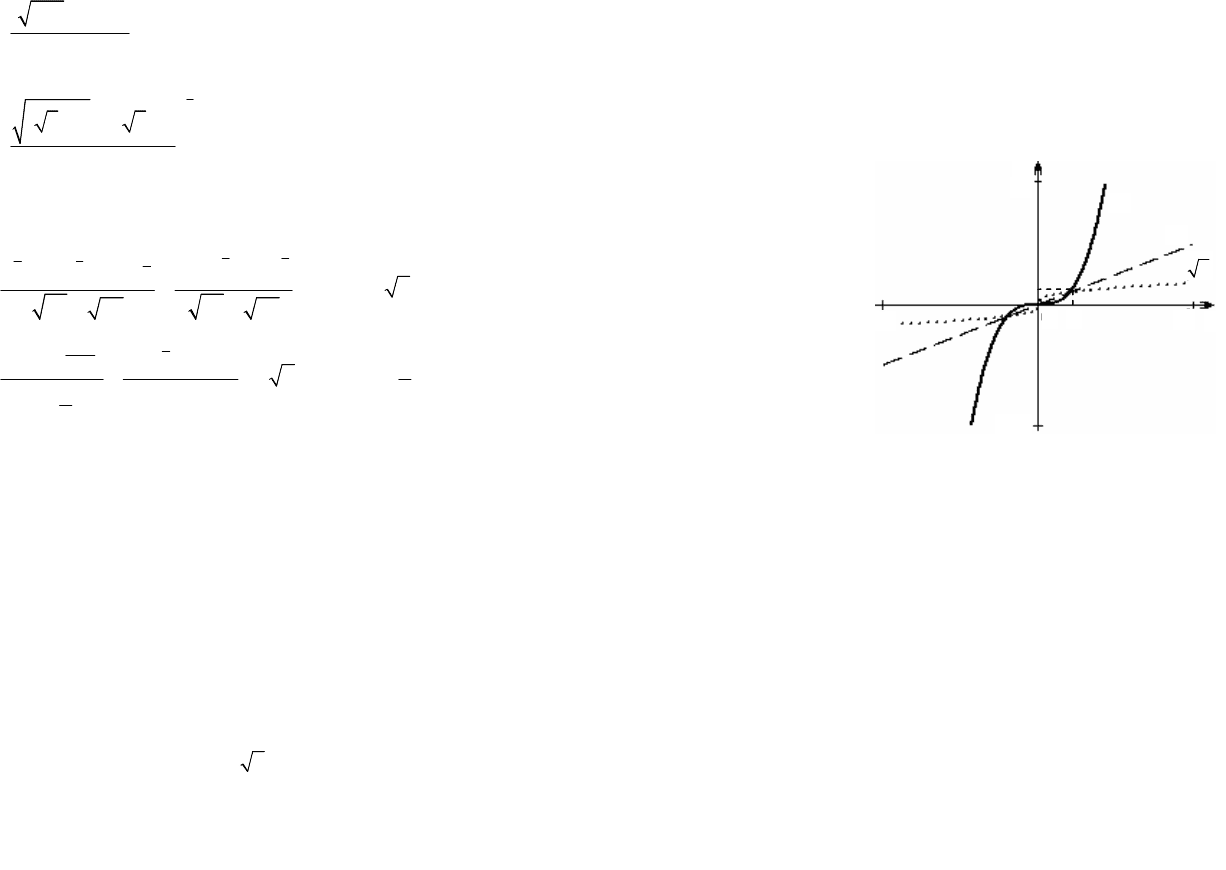
150 151
3)
(
)
(
)
(
)
111
71275125
177177177;
---
---
++++++++
4)
( )
( )
2,(6)
0,5
4
1
0,25
2,5
375
, ;
35
n
n
n
-
-
-
æö
ç÷
Î
ç÷
ç÷
×
èø
Z
5)
( ) ( )
( )
8
3
10,5
4
0,25
0,52,5
3493
, .
37
n
n
n
-
-
-
æö
ç÷
Î
ç÷
ç÷
×
ç÷
èø
Z
3.2. Найдите значение выражения:
1)
( )
( ) ( )
11
41
2
22
33
33
3
33
22
33
2
abab
aabab
aabaab
-+
+
--
при
22;
à =
2)
3
1
2
2
2
11,52
2,53
2
1
2
3,0,.
1
4
2
a
a
aa
aaa
aaa
aa
-
-
-
-
-
--
-
-
+=>¹
++
-
5.3. Степенная функция
Функция
,
yx
a
= где х – переменная величина,
a
– заданное
число, называется степенной функцией.
Если
1,
a
=
то
yx
=
– линейная функция, ее график – пря-
мая линия (см. параграф 4.3, рис. 4.7).
Если
2,
a
=
то
2
yx
=
– квадратичная функция, ее график –
парабола (см. параграф 4.3, рис. 4.8).
Если
3,
a
=
то
3
,
yx
= ее график – кубическая парабола (см.
параграф 4.3, рис. 4.9).
Степенная функция
3
.
yx
=
Это обратная функция для
3
.
yx
=
1. Область определения:
()(;).
Dy
=-¥+¥
2. Множество значений:
()(;).
Ey
=-¥+¥
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: x = 0 – единственный нуль.
6. Наибольшее и наименьшее значения функции: наибольше-
го и наименьшего значений функция не имеет.
7. Промежутки возрастания и убывания: функция является
возрастающей на всей области определения.
8. График функции симметричен графику кубической пара-
болы относительно прямой y = x и изображен на рис. 5.1.
Рис. 5.1
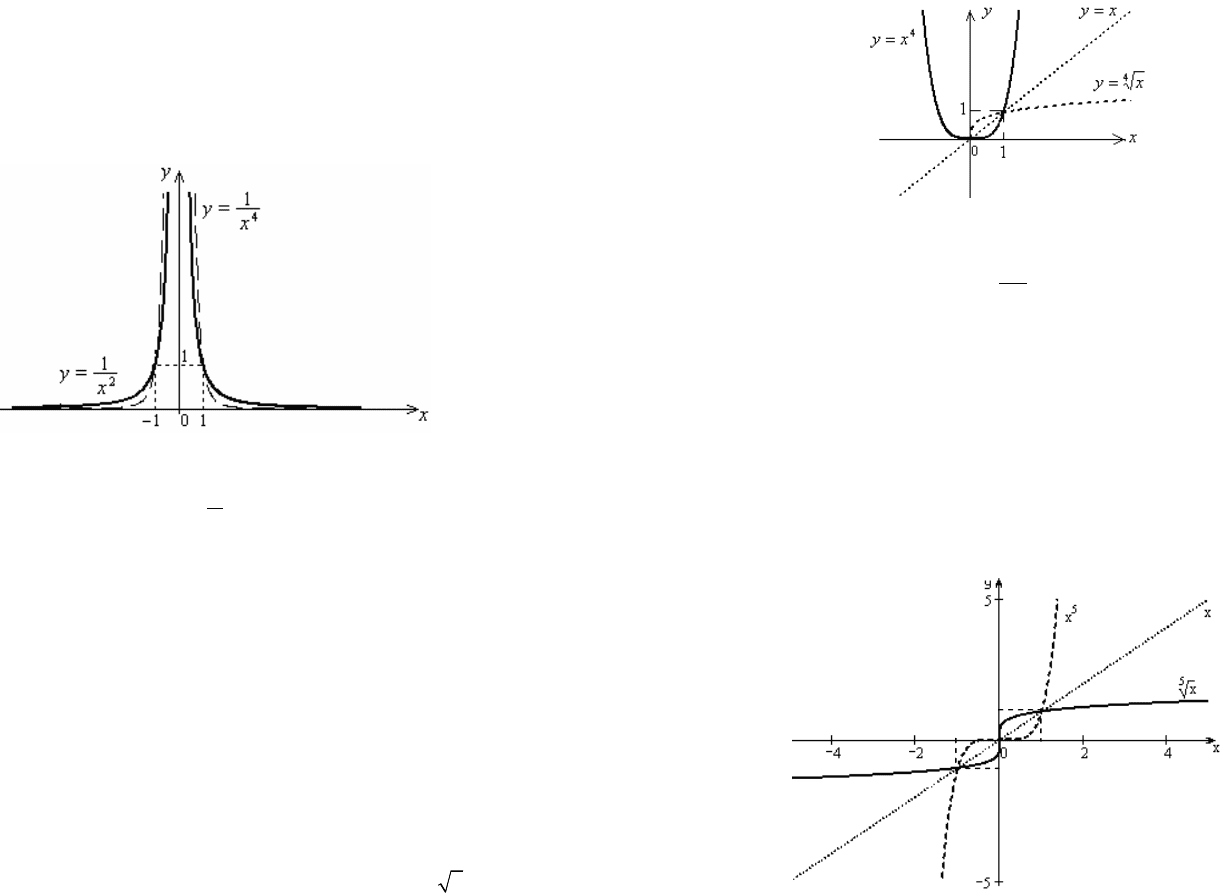
Степенная функция
2
,
n
yx
=
.
n
Î
N
1. Область определения:
()(;).
Dy
=-¥+¥
2. Множество значений:
[
)
()0;.
Ey
=+¥
3. Четность и нечетность: функция четная.
4. Периодичность функции: непериодическая.
5. Нули функции: единственный нуль x = 0.
6. Наибольшее и наименьшее значения функции: принимает
наименьшее значение для x = 0, оно равно 0.
7. Промежутки возрастания и убывания: функция является
убывающей на промежутке
(
]
;0
-¥ и возрастающей на проме-
жутке
[
)
0;.
+¥
8. График функции (для каждого n Î N) «похож» на график
квадратичной параболы
2
yx
=
(графики функций
2
,
yx
=
4
yx
=
изображены на рис. 5.2).
–
5
–10
5
0
10
у
х
х
х
3
3
õ
1
1
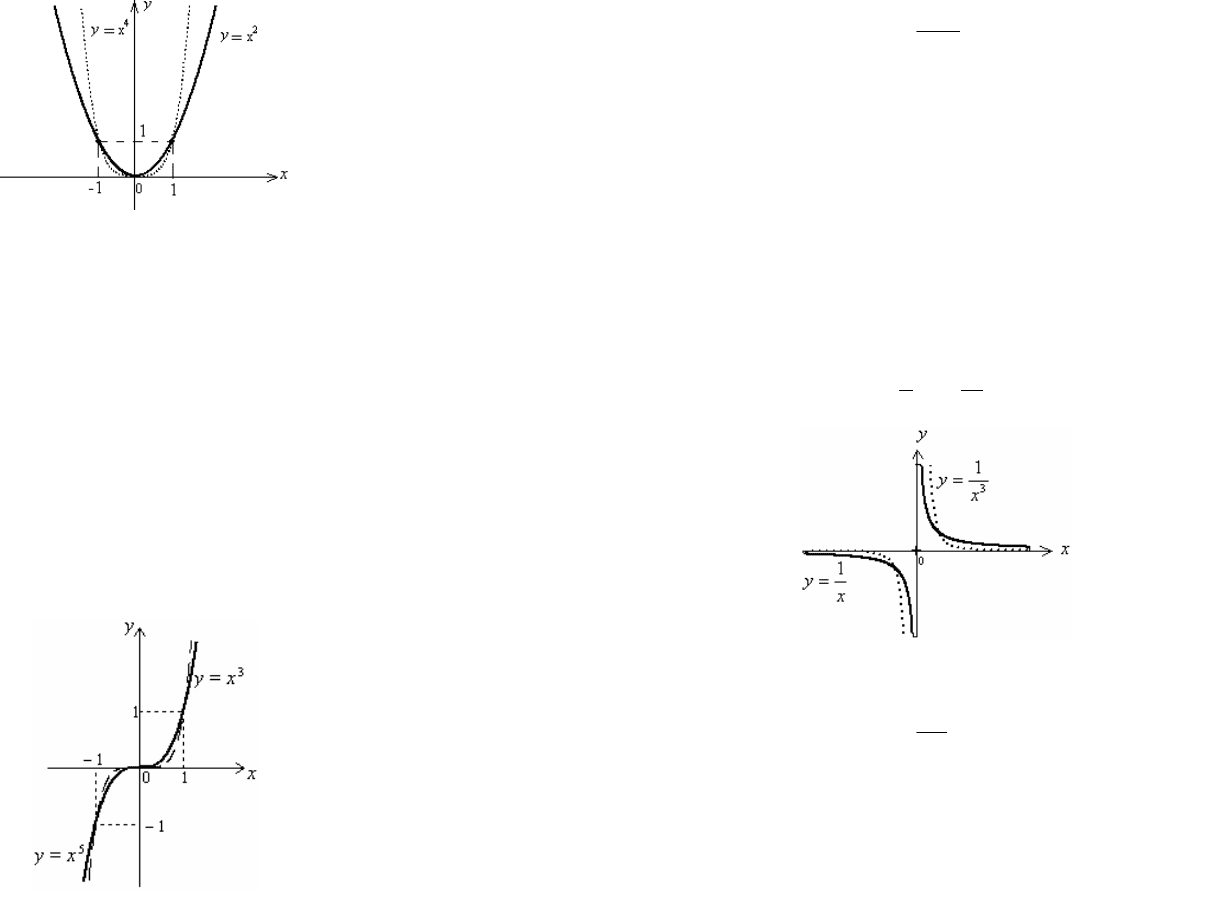
152 153
Рис. 5.2
Степенная функция
21
,
n
yx
+
=
.
n
Î
N
1. Область определения:
()(;).
Dy
=-¥+¥
2. Множество значений:
(
)
();.
Ey
=-¥+¥
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: x = 0 – единственный нуль.
6. Наибольшее и наименьшее значения: наибольшего и наи-
меньшего значений функция не имеет при любом
.
n
Î
N
7. Промежутки возрастания и убывания: функция является
возрастающей на всей области определения.
8. График функции (для каждого
n
Î
N
) «похож» на график
кубической параболы (графики функций
35
,
yxyx
==
изобра-
жены на рис. 5.3).
Рис. 5.3
Степенная функция
21
1
,.
n
yn
x
-
=Î
N
1. Область определения:
()(;0)(0;).
Dy
=-¥È+¥
2. Множество значений:
()(;0)(0;).
Ey
=-¥È+¥
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: нулей не имеет.
6. Наибольшее и наименьшее значения функции: наибольше-
го и наименьшего значений функция не имеет при любом
.
n
Î
N
7. Промежутки возрастания и убывания: функция является
убывающей в области определения.
8. Асимптоты:
0
x
=
(ось Оу) – вертикальная асимптота;
0
y
=
(ось Ох) – горизонтальная асимптота.
9. График функции (для любого n) «похож» на график гипер-
болы (графики функций
3
11
,yy
x
x
== изображены на рис. 5.4).
Рис. 5.4
Степенная функция
2
1
,
n
y
x
=
.
n
Î
N
1. Область определения:
()(;0)(0;).
Dy
=-¥È+¥
2. Множество значений:
()(0;).
Ey
=+¥
3. Четность и нечетность: функция четная.
4. Периодичность функции: непериодическая.
5. Наибольшее и наименьшее значения функции: наибольше-
го и наименьшего значений функция не имеет при любом
.
n
Î
N
154 155
6. Промежутки возрастания и убывания: функция является
возрастающей на
(
)
;0
-¥ и убывающей на
(
)
0;.
+¥
7. Асимптоты: x = 0 (ось Оу) – вертикальная асимптота;
y = 0 (ось Ох) – горизонтальная асимптота.
8. Графиками функций являются квадратичные гиперболы
(рис. 5.5).
Рис. 5.5
Степенная функция
1
2
,.
n
yxn
=Î
N
1. Область определения:
()[0;).
Dy
=+¥
2. Множество значений:
()[0;).
Ey
=+¥
3. Четность и нечетность: функция не обладает свойством
четности и нечетности.
4. Периодичность функции: непериодическая.
5. Нули функции: x = 0 – единственный нуль.
6. Наибольшее и наименьшее значения функции: наименьшее
значение, равное 0, функция принимает в точке x = 0; наиболь-
шего значения не имеет.
7. Промежутки возрастания и убывания: функция является
возрастающей на всей области определения.
8. Каждая такая функция при определенном показателе яв-
ляется обратной для функции
2
n
yx
= при условии
0.
x
³
9. График функции «похож» на график функции
yx
= при
любом n и изображен на рис. 5.6.
Рис. 5.6
Степенная функция
1
21
,.
n
yxn
-
=Î
N
1. Область определения:
()(;).
Dy
=-¥+¥
2. Множество значений:
()(;).
Ey
=-¥+¥
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: x = 0 – единственный нуль.
6. Наибольшее и наименьшее значения функции: наибольше-
го и наименьшего значений функция не имеет при любом
.
n
Î
N
7. Промежутки возрастания и убывания: функция является
возрастающей на всей области определения.
8. График функции изображен на рис. 5.7.
Рис. 5.7
1
1
–
1
–
1
