Матвеев Ю.Н. Основы теории систем и системного анализа

81

Рассмотрим систему трех уравнений-ограничений какой-то ОЗЛП,

записанных в стандартной форме:

⎪

⎩

⎪

⎨

⎧

++++=

,

34343332321313

24243232221212

14143132121111

bxaxaxaxay

(2.45)

где переменные x

1

, x

2

, x

3

, x

4

являются свободными, а y

1

, y

2

, y

3

– базисными.

Пусть требуется превратить переменную x

2

в базисную, а базисную

переменную y

3

сделать свободной. Такую замену переменных

символически обозначим как

32

yx

↔

.

Ранее была рассмотрена процедура замены переменных способом

подстановки. Такая процедура достаточно громоздкая, требующая

внимания, вероятность совершения ошибок в расчетах велика. Кроме того,

каждый раз нужно проделывать одни и те же операции, выполняемые по

определенным правилам. Эти правила реализованы в виде табличного

алгоритма.

Для упрощения расчетов по этому алгоритму необходимо

преобразовать

систему (2.45) к виду

⎪

⎩

⎪

⎨

⎧

−−−−−=

).(

),(

43433323213133

42432322212122

41431321211111

xaxaxaxaby

(2.46)

Обозначим

3434313112121111

;......;;.......;; aaaa −=

−

=

−

=

−=

α

. Тогда

система (2.46) примет вид

⎪

⎩

⎪

⎨

⎧

+++−=

).(

),(

43433323213133

42432322212122

41431321211111

xxxxby

αααα

(2.47)

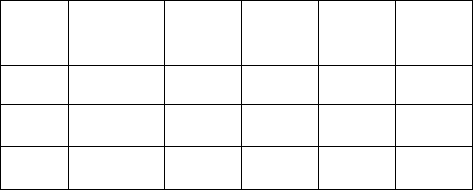
Запишем уравнения системы (2.47) в виде стандартной таблицы:

Своб.

член

x

1

x

2

x

3

x

4

y

1

b

1

11

α

12

α

13

α

14

α

y

2

b

2

21

α

22

α

23

α

24

α

y

3

b

3

31

α

32

α

33

α

34

α

Производим замену

32

yx

↔

. Выделим жирными линиями столбцы,

в которых расположен x

2

, и строку, в которой находится y

3

. Столбец x

2

называется разрешающим, а строка y

3

– разрешающей, коэффициент α

32

–

разрешающим элементом.

82

После выполнения замены

32

yx

↔

в строке, которая является

разрешающей, должен появиться x

2

, а в разрешающем столбце – y

3

.

Преобразуем разрешающую строку. Разрешим третье уравнение системы

(2.47) относительно x

2

:

),(

43433331313232

43433323213133

xxyxbx

xxxxby

αααα

α

+++−=

+

−=

).

1

(

4

32

34

3

32

33

23

32

1

32

31

32

3

2

xxxyx

b

x

α

αα

α

+++−= (2.48)

Для преобразования остальных строк подставим в первое уравнение

системы (2.47) вместо x

2

выражение (2.48):

−

⎩

⎨

⎧

⋅

+−=

⎪

⎭

⎪

⎬

⎫

++

⎥

⎦

⎤

⎟

⎠

⎞

++++

⎜

⎝

⎛

−

⎩

⎨

⎧

⎢

⎣

⎡

+−=→+++−=

32

312

11114143134

32

34

3

32

33

3

32

1

32

31

32

3

1211111141431321211111

1

)(

α

ααα

α

αα

α

αααααα

b

xbxxxxyx

b

xbyxxxxby

.

4

32

3412

14

3

32

3312

133

32

12

1

32

3112

11

32

312

1

4143134

32

3412

3

32

3312

3

32

12

1

32

3112

⎥

⎦

⎤

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−+

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−+

⎟

⎠

⎞

⎜

⎝

⎛

−

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−−

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−=

=

⎭

⎬

⎫

++

⋅

−

⋅

−−

⋅

−

x

xyx

b

xxxxyx

α

αα

α

αα

α

αα

α

αα

α

αα

α

αα

α

αα

Аналогичным образом преобразуются и остальные строки.

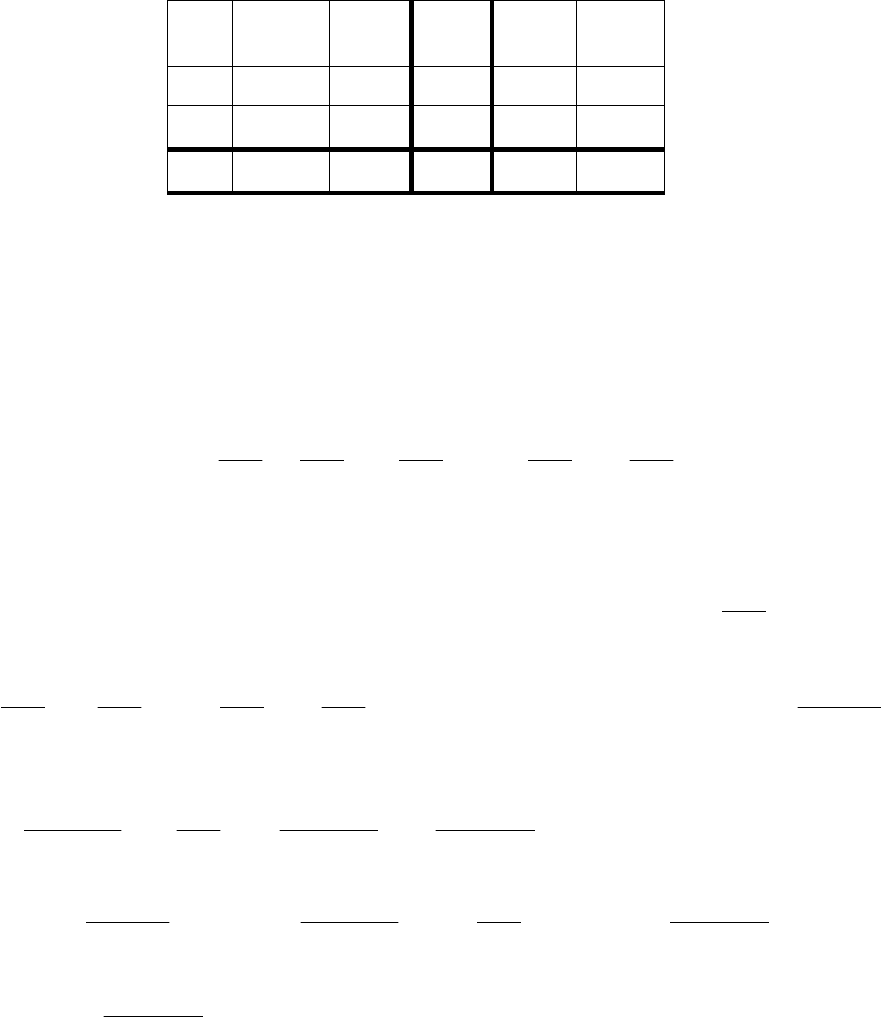
Полученные результаты занесем в таблицу, в которой замена

32

yx

↔

произведена:

Своб.

член

x

1

x

2

x

3

x

4

y

1

b

1

11

α

12

α

13

α

14

α

y

2

b

2

21

α

22

α

23

α

24

α

y

3

b

3

31

α

32

α

33

α

34

α

83

Своб.

член

x

1

y

3

x

3

x

4

y

1

32

312

1

α

b

⋅

−

32

3112

11

α

⋅

−

32

12

α

−

32

3312

13

α

⋅

−

32

3412

14

α

⋅

−

y

2

32

322

2

α

b

⋅

−

32

3122

21

α

⋅

−

32

22

α

−

32

3322

23

α

⋅

−

32

3422

24

α

⋅

−

x

2

32

3

α

b

32

31

α

32

1

α

32

33

α

32

34

α

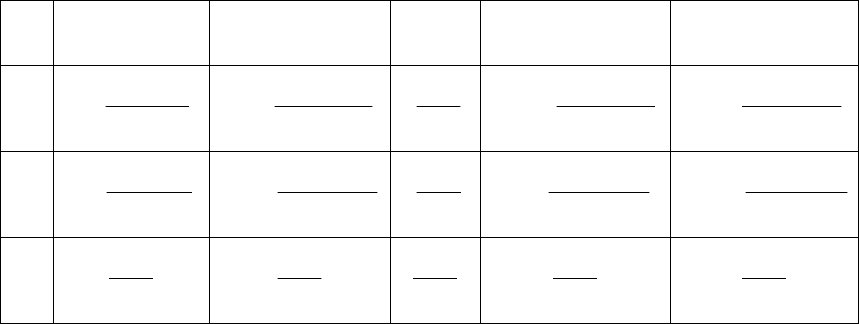
Теперь можно сформулировать алгоритм преобразования

коэффициентов стандартной таблицы:

1)

в новой таблице разрешающий элемент заменяется на обратную

ему величину;

2)

вместо коэффициентов разрешающей строки старой таблицы

проставляются коэффициенты, численно равные частному от деления

прежних элементов на разрешающий элемент;

3)

вместо коэффициентов разрешающего столбца старой таблицы

заносятся коэффициенты численно равные частному от деления прежних

элементов, взятых с противоположным знаком, на разрешающий элемент;

4) в остальные ячейки заносятся величины, численно равные

алгебраической сумме коэффициента старой таблицы, и произведения

элемента, расположенного в новой таблице в той же строке, что и первое

слагаемое суммы,

но из столбца, соответствующего разрешающему в

старой таблице, на коэффициент разрешающей строки старой таблицы,

расположенный в том же столбце, что и первое слагаемое суммы.

Словесной изящностью последний пункт не отличается, хотя на самом

деле преобразование довольно простое.

Пример 7

В системе уравнений-ограничений ОЗЛП осуществить замену

21

yx ↔ :

⎪

⎩

⎪

⎨

⎧

+−−=

−−=

+−=

−+−=

.2

,12

,52

314

323

212

3211

xxy

xxxy

(2.49)

Решение

Запишем систему (2.49) в стандартной форме:

⎪

⎩

⎪

⎨

⎧

+−=

+−−−=

+−−=

−+−−−=

).(2

),2(1

),2(5

314

323

212

3211

xxy

xxxy

(2.50)

84

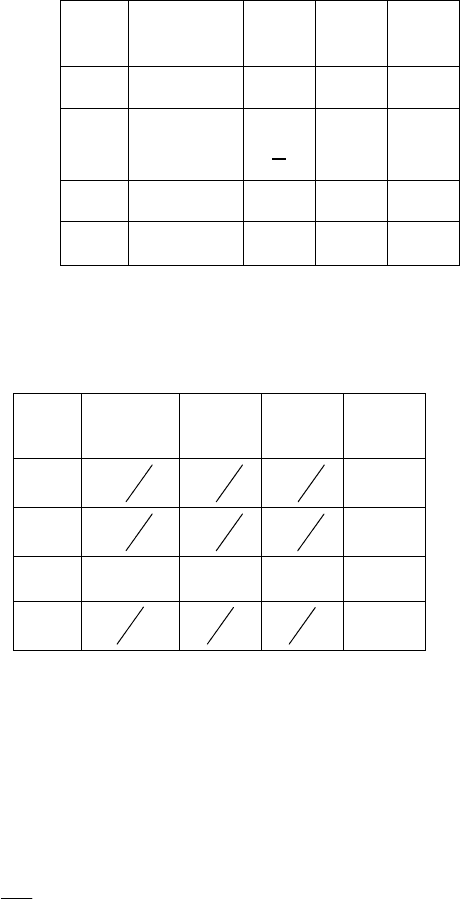
Внесем коэффициенты системы (2.50) в таблицу:

b

2

y

Своб.

член

x

1

x

2

x

3

y

1

–5 –1 1 –2

↔

1

x

y

2

1

2

1 0

y

3

–1 0 –2 1

y

4

2 1 0 1

Разрешающий коэффициент для замены

21

yx

↔

расположен на

пересечении строки y

2

и столбца x

1

: 2

21

−

=

α

. X

1

– разрешающий столбец,

y

2

– разрешающая строка. Строим таблицу:

Своб.

член

y

1

x

2

x

3

y

1

2

4

−

2

1

−

2

1

−

–2

x

1

2

1

−

2

1

−

2

1

−

0

y

3

–1 0 –2 1

y

4

2

5

2

1

2

1

«Переразрешение» системы (2.50)

21

yx

↔

завершено. Аналогичным

способом можно сделать любую замену

ij

yx

↔

. В задаче ЛП кроме

ограничений есть и целевая функция

nn

xcxcxccW ++

+

=

....

22110

,

которую в ОЗЛП необходимо минимизировать. Если производится замена

ij

yx ↔ , то это означает, что одна из свободных переменных x

r

становится

базисной, а одна из базисных переменных y

p

– свободной. Если в целевой

функции W

njx

j

,1, = свободные переменные, то после замены

pr

yx ↔

функция W примет вид

nnpp

xcycxcxccW

''

2

'

21

'

1

'

0

........ ++++++= .

Для такой замены переменных W полностью применим тот же

алгоритм, что и для ограничений ОЗЛП. Приводим функцию W к

стандартному виду:

)....(

22110 nn

xxxcW

γ

+

−= ,

где

nn

ccc −=−=−=

γ

...,,,

221

.

Вводим в стандартной таблице коэффициентов дополнительную

строку W:

85

Своб.

член

x

1

x

2

…

x

n

W

0

c

1

γ

2

γ

…

n

γ

y

1

b

11

α

12

α

…

n1

α

……………………………………………

y

m

b

1m

α

2m

α

…

mn

α

Преобразование коэффициентов производится точно так же, как и

для других строк стандартной таблицы. Однако строка W имеет

характерную особенность по сравнению с другими строками таблицы, а

именно: в строке W разрешающий элемент выбирать нельзя!

Пример 8

Произвести замену переменных

21

yx

↔

в ОЗЛП:

.0

,23

,3

2

1

,1

min,12

3,2,1

323

312

3211

321

≥

−=

−−=

−+−=

→

+

−

+

−

=

x

xxy

xxxy

xxxW

Преобразуем условия ОЗЛП в стандартную форму записи:

).23(0

),

2

1

(3

),(1

),2(1

323

312

3211

321

xxy

xxxy

xxxW

+−−=

+−−−=

−+−−−=

+

−

=

Заполним стандартную таблицу:

b

2

y

Своб.

член

x

1

x

2

x

3

W

1 1 –2 1

y

1

–1 –1 1 –1

↔

1

x

y

2

–3

–1/2

0 1

y

3

0 0 –3 2

Разрешающий элемент –1/2, разрешающая строка y

2

, разрешающий

столбец x

1

. Строим новую таблицу:

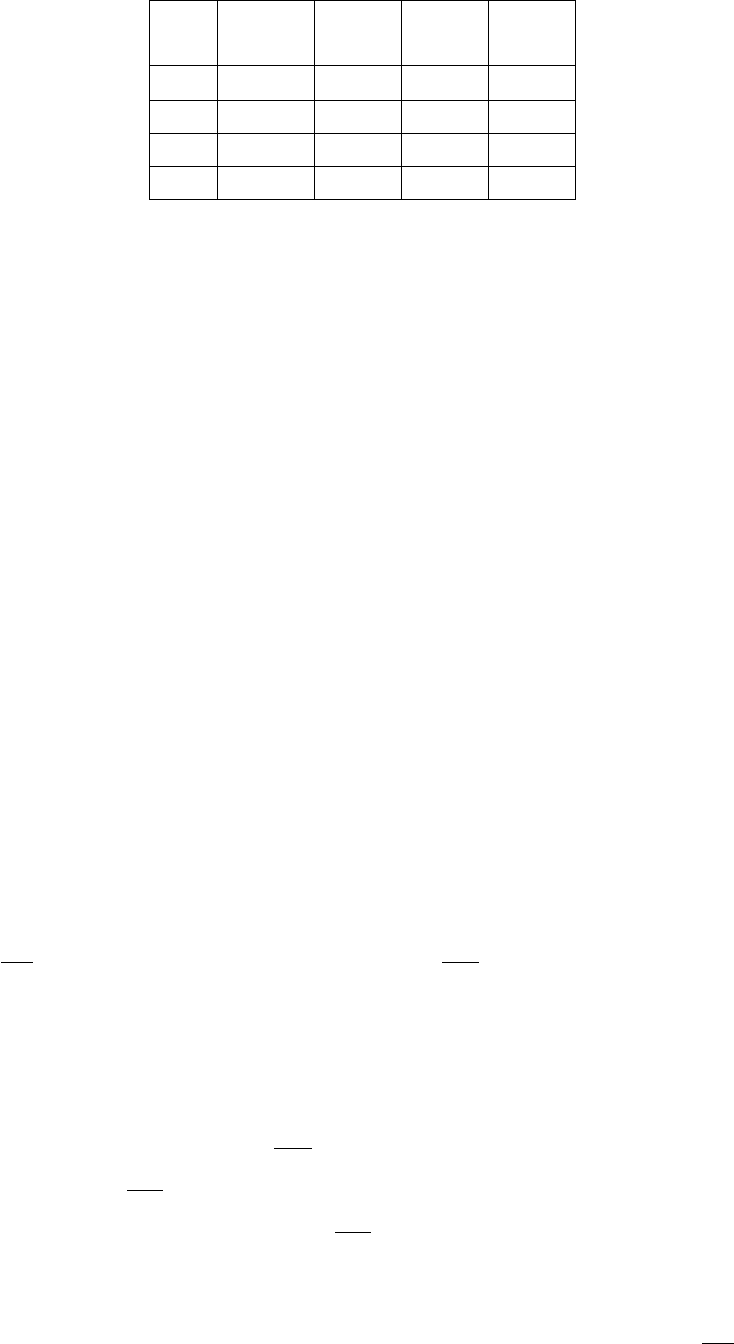
86

Своб.

член

y

2

x

2

x

3

W

–5 2 –2 3

y

1

5 –2 1 –3

x

1

6 –2 0 –2

y

3

0 0 –3 2

Заполняем ячейки, используя алгоритм «переразрешения». Замена

21

yx ↔ осуществлена.

Используя табличный алгоритм «переразрешения», можно решить

любую задачу ЛП. Определение решения ОЗЛП состоит из двух этапов:

1.

Отыскание опорного решения.

2.

Поиск оптимального решения.

В процессе выполнения первого этапа выясняется, имеет ли данная

ОЗЛП допустимые решения (имеет ли она вообще решение). Если задача

имеет допустимые решения, то определяется опорное решение. На втором

этапе путем перебора опорных решений выясняется, ограничена ли снизу

целевая функция. Если целевая функция не ограничена, оптимального

решения не существует

. Если целевая функция ограничена, то после ряда

замен

ij

yx ↔ находится оптимальное решение.

2.8. Определение опорного решения ОЗЛП

Пусть ОЗЛП приведена к стандартной форме записи:

);....(

22110 nn

xxxcW

γ

+

−=

⎪

⎩

⎪

⎨

⎧

+++−=

),....(

......................................................

),....(

2211

222212122

121211111

nmnmmmm

nn

xxxby

ααα

(2.51)

где

njx

j

,1, =

– свободные переменные; miу

i

,1, = – базисные. Ранее было

отмечено, что в каждой опорной точке (вершине) ОДР по крайней мере n

переменных из n+m должны быть равны нулю.

Положим, 0...

21

=

===

n

xxx , тогда

.;...;;

2211 mm

bybyby

=

(2.52)

Если в (2.52) все

mib

i

,1,0 =≥ , то опорное решение получено. Если

некоторые

prb

r

,1,0 =< , то решение не только не является опорным, но и

вообще недопустимо, т.к.

pry

r

,1,0 =< . Осуществляя замены

ij

yx ↔ ,

шаг за шагом мы или получим опорное решение, или докажем, что задача

ЛП не имеет решения. Задача ЛП не имеет решения, когда система

уравнений (2.51) не совместима с неравенствами

njx

j

,1,0 =≥

и

87

miy

i

,1,0 =≥ . Внешним признаком отсутствия допустимого решения

является отсутствие отрицательных коэффициентов в какой-то строке y

r

таблицы, где 0<

r

b . Тогда

),....(

2211 nrnrrrr

xxxby

α

+

−=

где

0<

r

b и

njx

jrnrr

,1,0,0....,,0,0

21

=≥≥≥≥

ααα

. В этом случае y

r

не

может стать неотрицательной величиной.

Пример 9

Пусть )322(10

3214

xxxy

+

+−

−

= . При 100

4321

−=→

=

yxxx .

Допустим, x

1

= 1, x

2

= 2, x

3

= 3. Тогда 25)942(10

4

−

=++

−

=

y ,

следовательно, опорного решения нет.

В случае, когда опорного решения нет, необходимо производить

замены

ij

yx ↔ так, чтобы после каждого «переразрешения» происходило

приближение к границе ОДР, т.е. с каждым шагом число отрицательных

базисных переменных должно убывать или, по крайней мере, убывали бы

по абсолютной величине отрицательные свободные члены. Для замены

ij

yx ↔ необходимо выбрать разрешающий элемент. Существует ряд

способов выбора разрешающего элемента для наиболее быстрого

движения к опорному решению. Суть одного из них заключается в

следующем.

Пусть в одном из уравнений системы (2.51) свободный член 0

<

r

b .

Рассматриваем в этой строке коэффициенты

rj

α

при свободных

переменных

njx

j

,1, = . Напомним, что если все nj

rj

,1,0 =>

α

, то задача

ЛП не имеет решения.

Пусть 0<

rp

α

. Выбираем столбец х

р

в качестве разрешающего, где

рассматриваем все коэффициенты

mi

ip

,1, =

α

, которые имеют одинаковые

знаки (плюс или минус) с соответствующими свободными членами

mib

i

,1, = . В качестве разрешающего выбирается тот коэффициент, для

которого отношение к нему соответствующего свободного члена

минимально:

mi

b

i

ip

rp

,1,min =→

α

.

Выбор разрешающего элемента однозначно определяет

разрешающую строку. Далее применяется процедура «переразрешения»,

т.е. замена

pr

xy ↔ .

Пример 10

Определить (если оно существует) опорное решение ОЗЛП.

Линейная функция W для простоты не приводится.

88

1

⎪

⎩

⎪

⎨

⎧

+−−=

+−=

−+−−−=

+

−

=

).(1

),(2

),2(5

),2(1

324

213

3212

3211

xxy

xxxy

Решение

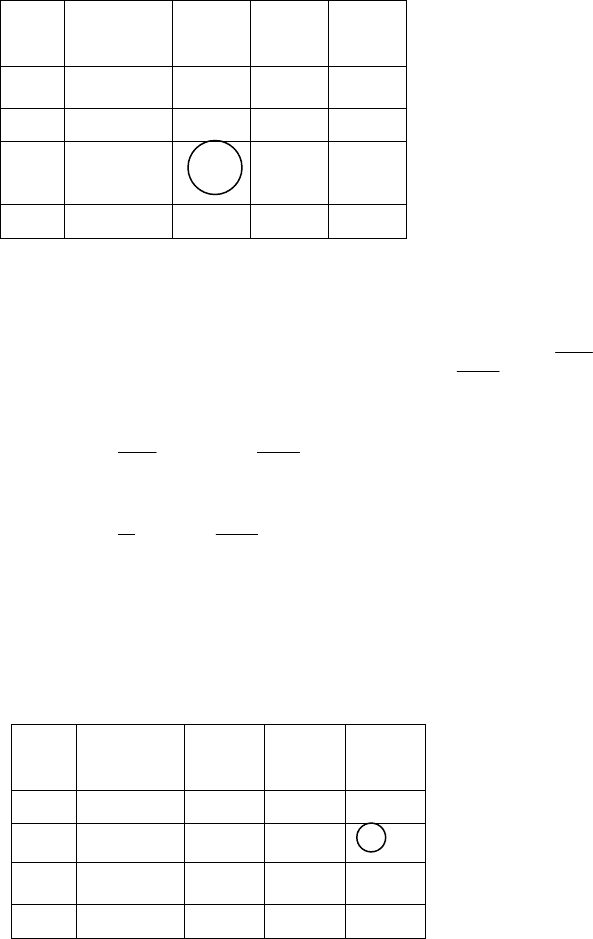
Запишем условия задачи в виде стандартной таблицы, где

05

2

<

−=b

:

у

3

↨

Своб.

член

х

1

х

2

х

3

у

1

1 –1 –2 1

у

2

–5 –2 1 –1

у

3

2 1 0

у

4

1 0 –1 1

В строке у

2

имеются 0,0

2321

<

α

. Это означает, что ОЗЛП имеет

решение (пока). Выбираем столбец х

1

(2

21

−

=

α

) в качестве разрешающего

и выбираем разрешающий элемент по правилу

mr

b

rp

r

rp

,1,min =→

α

:

.5,22

,2

1

2

,5,2

2

5

31

3

21

2

<

→=

−

α

b

Разрешающий элемент 1

31

=

α

. Производим замену

31

yx

↔

и получаем

таблицу, где b

2

< 0 ( 1

2

−=b ).

Своб.

член

у

3

х

2

х

3

у

1

3 1 -1 1

у

2

-1 2 3 -1

х

1

2 1 1 0

у

4

1 0 -1 1

По абсолютной величине b

2

меньше, чем был первоначально

abs (– 1) < abs (–5).

В строке y

2

с 01

2

<

−

=b есть отрицательный коэффициент

01

23

<−=

α

. Столбец x

3

разрешающий.

↕ у

2

х

1

↔

х

3

↔

89

Выбираем разрешающий элемент:

.1

1

;1

1

;3

1

3

43

4

23

2

13

1

===

−

===

ααα

bbb

Имеем два одинаковых отношения. Разрешающим выбираем

1

23

−=

α

. Строка у

2

разрешающая. Производим замену у

2

↔х

3

и получаем

таблицу:

Своб.

член

у

3

х

2

у

2

у

1

2 3 2 1

х

3

1 –2 –3 –1

х

1

2 1 1 0

у

4

0 2 2 1

Опорное решение получено:

.2,1,0,2,0

1341223

=

==

=

xxyyyxy

Пример 11

Найти опорное решение ОЗЛП (без строки W):

⎪

⎩

⎪

⎨

⎧

+−−−=

++−−=

+−−−=

).(2

),2(10

),(3

),2(4

214

3213

3212

211

xxy

xxxy

xxy

Решение

Запишем условия в стандартную таблицу:

Своб.

член

х

1

х

2

х

3

у

1

–4 –1 2 0

у

2

–3 1 –1 1

у

3

–10 2 –1 1

у

4

–2 1 0

В строке у

1

04

1

<−=b , опорного решения нет (пока). Коэффициент

01

11

<−=

α

. Значит столбец x

1

разрешающий. Определим разрешающий

элемент:

,2

1

2

,4

1

4

41

4

11

1

=

−

==

−

=

αα

bb

2 < 4,

Следовательно,

1

41

−=

α

– разрешающий элемент, строка у

4

разрешающая.

Производим замену х

1

↔у

4

и получаем таблицу:

х

1

↔

у

4

↕

–

1

90

Своб.

член

у

4

х

2

х

3

у

1

–2 –1 1 0

у

2

–5 1 0 1

у

3

–14 2 1 1

х

1

2 –1 1 0

В строке y

3

014

3

<−=b

. Однако все

.,,

333231

0 >

α

Запишем

).2(14

3213

xxxy ++−−= Очевидно, что ни при каких x

1

, x

2

, x

3

> 0 у

3

не

может стать нулевой или положительной величиной.

Вывод

Система ограничений не совместна, следовательно, ОЗЛП не имеет

решений (допустимых решений не существует).

2.9. Поиск оптимального решения ОЗЛП

Займёмся отысканием такого опорного решения (первое получено),

которое обращает в минимум линейную функцию

).....(

22110 nn

xxxcW

γ

+

−=

Покажем на примерах, как это делается.

Пример 12

Определить решение ОЗЛП. Пусть целевая функция

)(0

321

xxxW ++−−= при ограничениях

⎪

⎩

⎪

⎨

⎧

≥

−−=

+−=

+−−=

−+−=

.0

),2(2

),(5

),(1

),2(2

4,3,2,1

214

323

3212

3211

x

xxy

xxxy

Решение

Запишем условия ОЗЛП в виде стандартной таблицы:

Своб.

член

х

1

х

2

х

3

W

0 –1 1 –2

у

1

2 1 –2

у

2

1 1 –1 1

у

3

5 0 1 1

у

4

2 2 –1 0

х

2

↔

1

у

1

↕

Матвеев Ю.Н. Основы теории систем и системного анализа

Подождите немного. Документ загружается.