Матвеев Ю.Н. Основы теории систем и системного анализа

71

Подставим эти выражения в целевую функцию и, приводя подобные

члены, получим

.1225;1225

)12512382()32()33()65,0(2

)5()4(3)123()4(2

2121

22211121

221212121

−−−=−−−=

=−+−−++−+−+−−=++−−

−+−+

+

−

+

−

++

−

+= −−

xxWxx

xxxxxxxx

xxxxxxxxxW

Вернемся к ОДР, построенной для примера 2 (см. рис. 2.3). Основная

прямая для

21

25 xxWW −−=

′

→ . Построим основную прямую 0

=

′

W ,

12

2

5

0 xxW −=→=

′

(рис. 2.9).

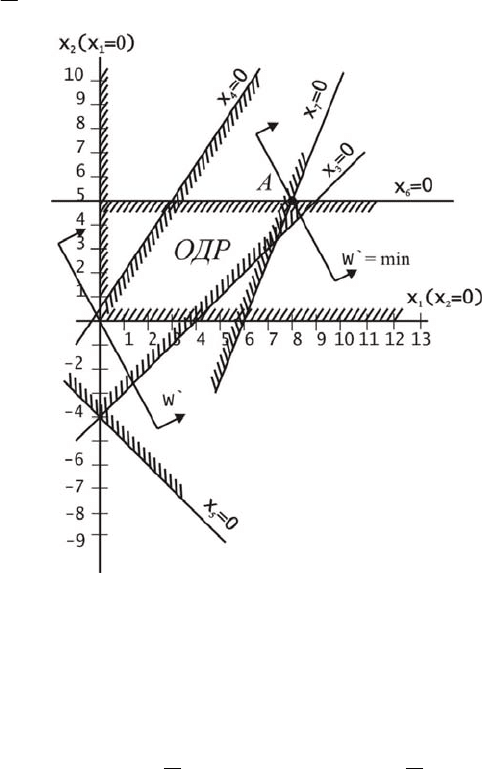
Рис. 2.9. Геометрическая интерпретация нахождения

оптимального решения ОЗЛП для примера 3

Прямая 0

=

′

W параллельна самой себе, и в т. А имеем оптимальное

решение. В т. А 0

0

6

=x и 0

0

7

=x , тогда 550

0

22

0

6

=→=+→= хxx .

Отсюда 5,806

2

5

06

2

1

0

1121

0

7

=→=++−→=++−→= xxxxx .

Таким образом,

.5,17455,8

,5,161525,83

,5,0455,8

,5;5,8

0

5

0

4

0

3

0

2

0

1

=++=

=+⋅−⋅=

=++−=

==

x

xx

Оптимальное решение:

.5,17;5,16;5,0;5;5,8

0

5

0

4

0

3

0

1

===== xxxxx

72

Определим минимум W:

.5,6412525,85

0

min

−=−⋅−⋅−=W

В итоге получим

.5,64695,4020

5,1735,165,0255,8232

0

7

0

6

0

5

0

4

0

3

0

2

0

1

0

min

−=−=⋅++

+⋅−−⋅+−=−+−−+−= xxxxxxxW

Анализ этого частного случая ОЗЛП (k = n-m = 2) позволяет сделать

выводы:

1.

Решение ОЗЛП, если оно существует, не может быть

расположено внутри ОДР. Оно может находиться только на границе ОДР.

2.

Решение ОЗЛП может быть неединственным (оптимальным).

Если основная прямая параллельна той стороне многоугольника

допустимых решений, где достигается минимум

W

′

, то этот минимум

достигается в любой точке этой стороны, т.е. имеет место бесчисленное

множество оптимальных решений.

3.

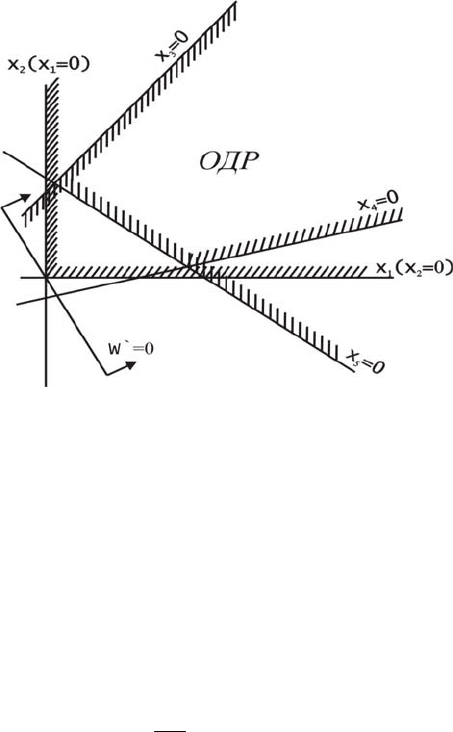
ОЗЛП может не иметь оптимального решения, даже если ОДР

существует, но эта ОДР открытая или неограниченная. Геометрическая

интерпретация этого варианта представлена на рис. 2.10.

Рис. 2.10. Геометрическая интерпретация решения ОЗЛП

(оптимальное решение отсутствует)

4. Оптимальное решение ОЗЛП достигается в одной из вершин

многоугольника допустимых решений. Случай бесчисленного множества

оптимальных решений также удовлетворяет этому выводу. Решение

ОЗЛП, находящееся в одной из вершин многоугольника ОДР, называется

опорным решением, а сама эта вершина – опорной точкой.

5.

Если число свободных переменных в ОЗЛП равно k = 2, а число

базисных переменных равно m и решение (оптимальное) ОЗЛП

существует, то оно всегда расположено в вершине ОДР, где по крайней

мере две из переменных

njx

j

,1, = равны нулю. Но бывают случаи, когда в

опорной точке пересекаются более двух прямых-ограничений. Тогда в

73

оптимальном решении равны нулю не две, а больше переменных. Это

случай ОЗЛП называется вырожденным.

6.

Интуитивно понятно, что для поиска оптимального решения

ОЗЛП необходимо проанализировать опорные решения (опорные точки

ОДР) и выбрать из них то, где линейная функция W достигнет минимума.

Подобные выводы можно сделать для любых количеств переменных

ЗЛП и уравнений-ограничений при условии m<n.

Оптимальное решение, если оно существует, находится не внутри, а

на

границе ОДР, в одной из опорных точек. В каждой опорной точке не

менее

k

переменных (k = n – m) ЗЛП равны нулю.

Для ускорения процедуры отыскания оптимального решения

необходимо отыскать сначала опорные точки (опорные решения) и,

целенаправленно анализируя эти опорные решения, определить минимум

целевой функции W.

2.5. Задача линейного программирования с ограничениями-

неравенствами. Переход к ОЗЛП и обратно [10]

В большинстве практических задач ЛП ограничения заданы не

уравнениями, а неравенствами. Переход от ЗЛП общего вида к ОЗЛП

осуществляется следующим образом.

Пусть имеется ЗЛП с

j

x , nj ,1= переменными. Ограничения задачи

ЛП имеют вид линейных неравенств. Знаки неравенств могут быть как ≥,

так и ≤.

Зададим все ограничения неравенства в стандартной форме записи:

⎪

⎩

⎪

⎨

⎧

≥+++

.

2211

,

22222121

11212111

....

..............................................

...

,...

mnmnmm

nn

bxaxaxa

(2.28)

Считаем, что все неравенства линейно независимы, т.е. никакое из

них нельзя представить в виде линейной комбинации других. Требуется

найти такую неотрицательную совокупность значений x

1

, x

2

, …¸x

n

, которая

удовлетворяла бы неравенствам системы (13) и, кроме того, обращала бы в

минимум линейную функцию

nn

xcxcxcW

+

= ....

2211

.

От поставленной таким образом ЗЛП легко перейти к ОЗЛП.

Перепишем систему (2.28) в виде

⎪

⎩

⎪

⎨

⎧

++++=

,...

.....................................................

,...

...

2211

222221212

,

112121111

mnmnmmm

nn

bxaxaxay

(2.29)

74

где y

1

, y

2

, …, y

m

– новые переменные, которые называются

дополнительными.

Из системы (2.29) следует, что дополнительные y

i,

mi ,1= , так же как

и основные x

j

, nj ,1= , должны быть неотрицательными.

Появилась новая постановка задачи ЛП: определить такие

неотрицательные значения n+m переменных x

j

, nj ,1= и y

i,

mi ,1= ,

которые удовлетворяли бы системе уравнений (2.29) и обращали бы в

минимум линейную функцию

.0...00....

212211 mnn

yyyxcxcxcW ⋅

+

⋅

+

⋅

+

++=

Это ОЗЛП. Уравнения в системе заданы в виде, когда базисные

переменные y

i

mi ,1= уже выражены через свободные x

j

, nj ,1= . Общее

количество переменных увеличилось на m, но задача сведена к ОЗЛП.

Пример 4

Определить минимум

321

32 xxxW

−

=

при ограничениях

⎪

⎩

⎪

⎨

⎧

=≥

≤−

−≥+−

−≤−

≤+−

.,1,0

,0

,12

,13

,632

15

145

23

321

njx

xx

xxx

xx

xxx

j

(2.30)

Привести эту задачу к ОЗЛП.

Решение

Приведем неравенства (2.30) к стандартной форме:

⎪

⎩

⎪

⎨

⎧

≥+−

≥++−

≥−+−

≥

+

−

+

−

.0

,012

,013

,0632

15

145

23

321

xx

xxx

xx

xxx

Введем дополнительные переменные:

⎪

⎩

⎪

⎨

⎧

−=

++−=

−−=

+

−

+

−

=

.

,12

,13

,632

514

5413

322

3211

xxy

xxxy

xxy

xxxy

(2.31)

Задача ЛП сводится к поиску x

j

≥ 0, 5,1=j , y

i

≥ 0, 4,1=i , которые бы

удовлетворяли (2.31) и приводили бы к минимуму

321

32 xxxW −

−

=

.

Переход от уравнений-ограничений к неравенствам может быть

произведен следующим образом:

75

имеем

⎪

⎩

⎪

⎨

⎧

=+++

;....

..............................................

,

...

,...

2211

2

2222121

11212111

mnmnmm

nn

bxaxaxa

перепишем

⎪

⎩

⎪

⎨

⎧

≥+++≥

.....

..............................................

,...

2211

222221212

112121111

mnmnmmm

nn

bxaxaxab

Пример 5

Эта система после введения 2m дополнительных переменных будет

выглядеть так:

⎪

⎩

⎪

⎨

⎧

=+−

−=−

=+

;1

,32

,1

543

32

21

xxx

xx

⎪

⎩

⎪

⎨

⎧

≥+−+−

≥−+−

≥+−

≥+−−

≥

−

+

.01

,01

,032

,01

543

32

21

xxx

xx

Вводим дополнительные переменные y

i

≥ 0,

6,1=i

:

⎪

⎩

⎪

⎨

⎧

+−+−=

−+−=

+−=

+−−=

−

+

=

.1

,1

,32

,1

5436

5435

324

323

212

211

xxxy

xxy

Физический смысл дополнительных переменных, особенно при

таких преобразованиях, не всегда понятен и требует тщательного

осмысливания.

2.6. Симплекс-метод решения задачи линейного программирования

Идея симплекс-метода относительно проста. Пусть в ОЗЛП имеется

n переменных и m независимых линейных ограничений, заданных

76

уравнениями. Известно, что оптимальное решение ОЗЛП, если оно

существует, достигается в одной из вершин ОДР (опорной точке), где не

менее k = n-m переменных задачи равны нулю [10].

Выберем в ОЗЛП какие-то k переменных в качестве свободных и

выразим m базисных переменных через свободные.

Пусть свободные переменные имеют вид x

1

, x

2

, …, x

k

, тогда

базисные переменные запишем так:

⎪

⎩

⎪

⎨

⎧

++++=

+

=

+++++

+++

+

.

,22,11,

2,222,211,22

,

1,122,11

1,1

1

....

,....

....

nkknnnn

kkkkkkk

kkkkk

k

βxaxaxax

(2.32)

Положим,

0,.....,0,0

21

=

==

k

xxx . Получим

nnkkkk

xxx

β

=

++++

,.....,

2211

.

Это решение ОЗЛП. Оно допустимо, если все свободные члены

неотрицательные, т.е.

0,.....,0,0

21

≥≥≥

++ nkk

β

.

Предположим, что это так. Тогда полученное решение опорное.

Выясним, оптимально ли полученное решение?

Выразим линейную функцию W через свободные переменные x

1

, x

2

,

…, x

k

:

kk

xxxW

γ

+

+= ...

22110

→

min. (2.33)

Для полученного опорного решения x

1

= 0, x

2

= 0, …, x

k

= 0;

0

γ

=W .

Посмотрим, нельзя ли улучшить (оптимизировать) решение, т.е.

уменьшить функцию W, увеличивая в положительную сторону какие-то

переменные x

1

, x

2

, …, x

k

. (Уменьшить их нельзя, т.к. они станут

отрицательными, что недопустимо по условиям ЛП).

Если все

kjγ

j

,1, =

в (2.33) неотрицательны (≥0), то при увеличении

каких-либо переменных x

1

, x

2

, …, x

k

в положительную сторону невозможно

уменьшить W (значение W будет возрастать). Следовательно, найденное

опорное решение

,,0,0,0

1121 ++

=

===

kkk

xxxx

β

nnkk

xx

β

=

++

,...,

22

является оптимальным и .

0

min

γ

=W

Вывод

Если в (2.33) все

kjγ

j

,1, = неотрицательны, то полученное ранее

опорное решение ОЗЛП является оптимальным. Наоборот, если среди

kjγ

j

,1, = есть отрицательные, то увеличение при них каких-то

переменных из x

1

, x

2

, …, x

k

приведет к уменьшению W, т.е. улучшит

решение. Например, пусть в (2.33)

0

1

≤

γ

. Значит, если увеличивать x

1

, т.е.

переходить от полученного опорного решения к другому, где 0

1

≠x , а

77

какая-то переменная 0=

+ pk

x , можно добиться уменьшения значения W.

Однако увеличивать x

1

следует осторожно, чтобы переменные x

k+1

, x

k+2

, …,

x

n

(в них входит x

1

как свободная) не стали отрицательными.

Проанализируем случаи, когда увеличение в положительную

сторону x

1

может сделать какие-то из переменных x

k+1

, x

k+2

, …, x

n

отрицательными. Это может произойти, если в каком-то (каких-то)

уравнении системы (2.32) коэффициент

1,р

a при x

1

отрицателен, если же

коэффициенты при x

1

строго положительны, то x

1

можно увеличивать

беспредельно, а значит линейная функция W не ограничена снизу, и

оптимального решения ОЗЛП не существует.

Допустим, что среди уравнений системы (2.32) имеются такие, в

которых коэффициент при x

1

отрицателен.

Выберем одно из уравнений, где базисной переменной является

ekeeiee

xaxaxax

k

β

+

+= ...

2

21

. Как отмечено выше, 0>

e

β

, а

0

1

<

e

a

.

Оставляем x

2

= x

3

=…= x

k

= 0.

Имеем

e

βxax

+

=

1

. (2.34)

Из (2.34) видно, что увеличивать x

1

можно только до величины

.,0

1

e

a

β

xx −==

Если x

1

будет больше

1

e

a

β

−

, то x

e

станет отрицательной, что не-

допустимо по условиям ОЗЛП. Определим ту из переменных x

k+1

, x

k+2

, …,

x

n

, в которой коэффициент при x

1

в уравнениях отрицателен.

Тогда очевидно, что раньше всех в нуль обратится та базисная

переменная, для которой отношение

min

1

→−

e

a

β

.

Пусть этой переменной будет x

r

. Тогда имеет смысл для улучшения

решения ОЗЛП «переразрешить» систему (2.32), выведя x

1

из числа

свободных переменных и сделав ее базисной, и, наоборот, базисную

переменную x

r

сделать свободной в новом решении, где x

r

будет равна 0.

Необходимо перейти от опорного решения ,0,0,0

21

=

==

k

xxx

nnkkkk

xxx

β

=

==

++++

,...,,

2211

к другому опорному решению

,0...

32

=====

rk

xxxx

,,,

112211 −−++++

=

rrkkkk

xxx

β

,...,

11 +

=

+ rr

x

β

nn

x

β

= .

Получим новую систему уравнений типа (2.32). Тогда можно

выразить через новые свободные переменные и целевую функцию

rrkk

xxxW

''

2

'

2

'

0

...

γγγγ

++++=

. (2.35)

78

Проанализируем коэффициенты

'''

3

'

2

,,...,,

rk

γγγγ

в (2.35). Если они

неотрицательны, то полученное опорное решение оптимально в смысле

минимума W. Задавая новые свободные переменные

,0...

232

===== xxxx

k

получим минимум

'

0

γ

=W . Если же среди

коэффициентов

1,2, += kjγ

j

есть отрицательные, система (2.32),

полученная из (2.35), вновь «переразрешается» относительно других

базисных переменных и так далее, пока не будет найдено оптимальное в

смысле минимума значение W. Особо следует отметить, что все

вышесказанное справедливо для опорных решений, все

nkpβ

p

,1,0 +=>

.

Пример 6

Определить

min

31

25 xxW

−

=

(2.36)

при ограничениях

⎪

⎩

⎪

⎨

⎧

≥

≤+−

≤++−

≤+−−

.0,,,

,753

,5

,225

4321

41

431

321

хххх

xx

xxx

(2.37)

Решение

Приведем неравенства к стандартному виду умножением левых и

правых частей неравенств системы (2.27) на –1:

⎪

⎩

⎪

⎨

⎧

−≥−

−≥−−−

−≥−+

.753

,5

,225

41

431

321

xx

xxx

Вводя дополнительные переменные y

1

≥0, y

2

≥0, y

3

≥0 и назначив их

базисными, получим

⎪

⎩

⎪

⎨

⎧

+−=

+−−−=

+−+=

.753

,5

,225

413

4312

3211

xxy

xxxy

(2.38)

Общее число переменных n = 7, число уравнений m = 3. Поэтому

число свободных переменных k = n – m =7 – 3 = 4.

Пусть свободные переменные x

1

, x

2

, x

3

, x

4

. Положим, x

1

= x

2

= x

3

= x

4

= 0.

Из (2.38) получаем y

1

= 2, y

2

= 5, y

3

= 7.

Имеем опорное решение (все переменные ≥0) x

1

= x

2

= x

3

= x

4

= 0;

y

1

= 2, y

2

= 5, y

3

= 7. Для такого опорного решения W = 0.

Полученное решение неоптимальное в смысле минимума W, потому

что в (2.36) коэффициент при x

3

отрицателен, значит, увеличивая x

3

в

положительную сторону, можно уменьшить W.

79

Определим, насколько (до какого численного значения) можно

увеличивать x

3

, чтобы полученное решение было допустимым и опорным.

Рассмотрим систему (2.38). В уравнении для y

1

и y

2

коэффициенты

2

13

−=a и 1

23

−

=a . При увеличении x

3

переменные y

1

и y

2

могут стать

отрицательными, что недопустимо.

Какая из переменных, y

1

или y

2

, быстрее станет отрицательной при

увеличении x

3

? При каком минимальном значении x

3

переменная y

1

или y

2

станет равной нулю?

Положим, в (2.38) 02250

3211

=

+

−

+

→

=

xxxy . Если 0

21

=

= xx

(опорное решение), то x

3

= 1 и y

1

= 0,

050

4312

=+

−

→

=

xxxy

. Если

0

41

== xx , то x

3

= 5 и y

2

= 0. Значит, наиболее угрожаемая, чувствительная

базисная переменная – y

1

(она становится равной 0 при x

3

=1). Вводим y

1

в

число свободных переменных, а x

3

– базисных. «Переразрешаем» систему

(2.38) относительно базисных переменных x

3

, y

2

, y

3

. При этом x

1

, x

2

, y

1

, y

4

станут свободными переменными. Из первого уравнения (2.38) имеем

1

2

1

2

1

2

5

1213

+−+= yxxx . (2.39)

Подставим выражение (2.39) для x

3

во второе уравнение (2.38):

4

2

1

2

1

2

3

51

2

1

2

1

2

5

4121412112

+−+−−=+−−+−−= xyxxxyxxxy .

Уравнение y

3

в (2.38) не содержит x

3

и не изменится. Получаем

систему

⎪

⎩

⎪

⎨

⎧

+−=

+−+−−=

+−+=

.753

,4

2

1

2

1

2

3

,1

2

1

2

1

2

5

413

41212

1213

xxy

xyxxy

yxxx

(2.40)

Выразим линейную функцию (2.36) через новые свободные

переменные x

1

, x

2

, x

3

, x

4

:

2)1

2

1

2

1

2

5

(2525

12121131

−+−=+−+−=−= yxyxxxxxW ,

2

12

−

+

−

=

yxW . (2.41)

Для данного опорного решения x

1

= x

2

= y

1

= x

4

= 0; x

3

= 1, y

2

= 4, y

3

= 7,

W = 0 + 0 – 2= –2.

Новое значение W = –2, прежнее W = 0. Является ли полученное

значение W оптимальным? Нет, потому что коэффициент при x

2

в (2.41)

отрицателен, т.е. 1

'

2

−=γ . Значит нужно ввести x

2

в состав базисных

переменных, а одну из базисных переменных системы (2.40) сделать

свободной. Этой переменной будет y

2

, т.к. в уравнении системы (2.40)

80

коэффициент при x

2

отрицателен. В уравнении для x

3

коэффициент при x

2

положителен, а в уравнении для y

3

переменной x

2

нет.

Делаем x

2

базисной переменной, а y

2

свободной:

.823

,4

2

1

2

1

2

3

1212

++−−=

yyxx

yxxy

Подставим полученное для x

2

выражение в уравнение для x

3

в (2.40)

и получим

.514

2

3

2

5

1

2

1

)823(

2

1

2

5

4214

2111412113

+−−=+−+

+−+=+−+−+−−+=

xyxx

yxxyxyyxxx

В уравнение (2.40) для y

3

переменная x

2

не входит. Получим новую

систему

⎪

⎩

⎪

⎨

⎧

+−=

++−−=

+−−=

.753

,823

,5

413

1212

4213

xxy

yyxx

xyxx

(2.42)

Выразим W из (2.41) через свободные переменные системы (2.42):

.10232823

2)823(2

2121

112112

−+=−++=

=−

+

−

=

−

+−=

yxyx

yyyxyxW

(2.43)

Подставив значение переменной

3

х из (2.42) в (2.36), получим

.102231022

25)5(2525

42142

11421131

−++=−++

+−

=

+

−

=

−=

xyxxy

xxxyxxxxW

(2.44)

Задавая свободные переменные x

1

= x

4

= y

1

= y

2

= 0, получим в обоих

случаях W = –10.

Это решение оптимально, т.к. в выражениях (2.43) и (2.44) для W все

коэффициенты при свободных переменных положительны.

Оптимальное решение

.10,7,0,0,0,5,8,0

0

min

0

3

0

2

0

1

0

4

0

3

0

2

0

1

−======== Wyyyxxxx

2.7. Табличный алгоритм замены базисных переменных

на свободные и наоборот

Процедура «переразрешения» системы уравнений-ограничений

ОЗЛП относительно новых базисных переменных может быть

существенно упрощена. Этого можно достигнуть, если производить

вычисления по алгоритму в стандартных таблицах. Рассмотрим алгоритм

на конкретном примере. Вопросы работоспособности алгоритма в общем

случае не обсуждаются, а считается, что алгоритм справедлив и для

общего случая.

Матвеев Ю.Н. Основы теории систем и системного анализа

Подождите немного. Документ загружается.