Матвеев Ю.Н. Основы теории систем и системного анализа
Подождите немного. Документ загружается.

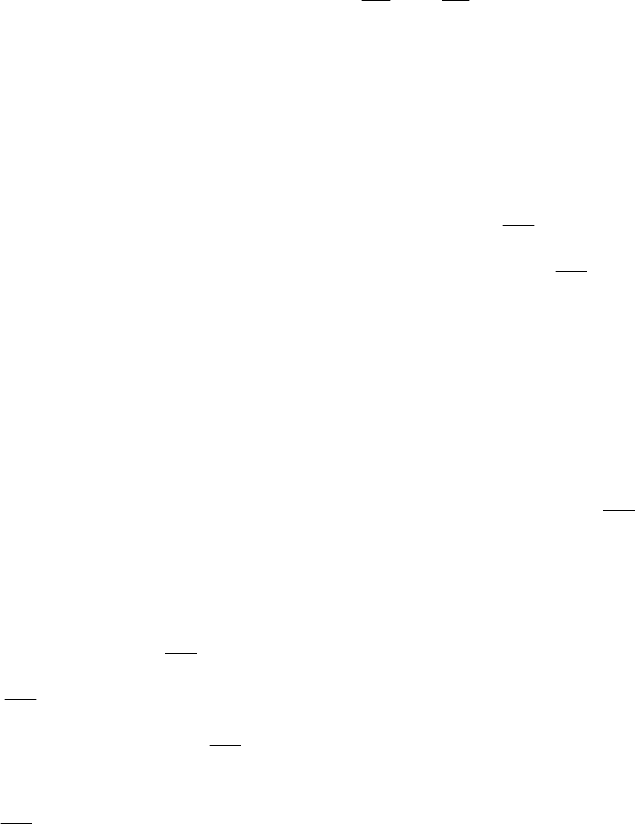
61
Теперь математическую модель операции можно записать как
()( )
(
)
max
232313133222212122212111111
→
+
+
+
++= xaxaCxaxaCxaxaCW (2.12)
при ограничениях
,
,
,
,
,
2232221
1131211
3232313133
2222212122
1212111111
Nxxx
Nxxx
βxaxab
βxaxab
βxaxab
=++
=++
≤+≤
≤+≤
≤
+
≤
(2.13)
где
.3,1,2,1,0 ==≥ jix
ij
(2.14)
Итак, мы рассмотрели несколько задач исследования операций.
Можно выделить характерные черты, которые объединяют эти задачи:
•
элементы решения
n
xxx ,...,,
21
должны быть неотрицательными;
•
требуется определить такие значения
0,...,,
00
2
0
1
≥
n
xxx
, чтобы
выполнялись некоторые ограничения, имеющие вид линейных неравенств
или равенств относительно переменных
njx
j
,1, = , и при этом некоторая
линейная функция
W тех же переменных njx
j
,1, = обращалась бы в
минимум или максимум.
Для решения подобных задач разработан специальный
математический аппарат, который носит название линейного
программирования (планирования). А нужен ли специальный
математический аппарат? Может быть, необходимо, как это принято при
поиске экстремумов функций многих переменных в математике, взять
частные производные по всем переменным
njx
j
,1, = функции W ,
приравнять их к нулю и найти точку экстремума? По знаку вторых
производных или методом приращений определить вид экстремума. Но в
виду линейности функции
W сделать этого нельзя. Производные по
аргументам
njx
j
,1, = функции W будут константами, равными
njC
j
,1, = , т.е. ни одна частная производная не будет равна нулю ни при
каких значениях
njx
j
,1, = . Максимум или минимум функции W , если он
существует, достигается всегда где-то на границах возможных значений
njx
j
,1, = , т.е. там, где начинают действовать ограничения.
Математический аппарат линейного программирования позволяет
последовательно и довольно быстро обследовать границы области
возможных решений и найти на этих границах решение задачи или
доказать, что оно не существует.

62
2.3. Основная задача линейного программирования
Задача линейного программирования (ЗЛП) с ограничениями-
равенствами называется основной задачей линейного программирования
(ОЗЛП) [10].
ОЗЛП ставится следующим образом: имеется ряд переменных
n
xxx ,...,,
21
. Требуется определить такие неотрицательные значения этих
переменных, которые удовлетворяли бы системе линейных уравнений
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
mnmnmm
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
...
..............................................
,...
,...
2211
22222121
11212111
(2.15)
и, кроме того, обращали бы в минимум линейную функцию
....
2211 nn
xCxCxCW
+
+
+
= (2.16)
Случай, когда необходимо определить максимум линейной функции,
легко сводится к предыдущему. Для этого необходимо только изменить
знак функции
W и рассматривать функцию
nn
xCxCxCWW
−
−
−
−
=
−=
′
...
2211
, (2.17)
т.е.
()
WW −= minmax и
(
)
WW minmax
−
=
.
Будем называть допустимым решением ОЗЛП любую совокупность
переменных 0,...,0,0
21
≥≥≥
n
xxx , которая удовлетворяет уравнениям-
ограничениям (2.15).
Оптимальным решением будем называть то из допустимых решений
00
2
0
1
,...,,
n
xxx , при котором линейная функция (2.17) обращается в минимум.
Рассмотрим прежде всего вопрос о существовании допустимых
решений ОЗЛП.
Определение
Рангом матрицы называется наибольший порядок отличного от нуля
определителя, который можно получить, вычёркивая из матрицы какие-то
строки и столбцы.
Матрицей системы уравнений
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
mnmnmm
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
...
..............................................
,...
,...
2211
22222121
11212111
(2.18)
называется матрица, составленная из коэффициентов
njmia
ij
,1,,1, == при
njx
j
,1, = :

63
mnmm
n
n
ij
aaa
aaa
aaa
njmiaA
...
...
...
,1,,1,
21
22221
11211
⋅⋅⋅⋅
==== . (2.19)
Расширенной матрицей системы линейных уравнений называется
матрица
A
, дополненная столбцом свободных членов mib
i
,1, = :
mmnmm
n
n
p
baaa
baaa
baaa
A
...
...
...
21
222221
111211
⋅⋅⋅⋅⋅
= . (2.20)
В линейной алгебре доказывается, что для совместности системы
линейных уравнений (2.18) необходимо и достаточно, чтобы ранг матрицы
системы
A
был равен рангу её расширенной матрицы
p
A . Этот общий
ранг
r
называется рангом системы и численно равен количеству линейно
независимых уравнений-ограничений ОЗЛП.
Очевидно, что ранг системы не может быть больше числа уравнений m :
m
r
≤
,
и ранг системы не может быть больше общего числа переменных n :
n
r
≤
.
Структура задачи ЛП существенно зависит от ранга системы
ограничений (2.15).
Рассмотрим случай, когда n
r
=
, т.е. nm
=
. В этом случае число
линейно независимых уравнений, входящих в систему (2.15), равно числу
переменных. Система уравнений-ограничений ОЗЛП в этом случае имеет
вид
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
....
..............................................
,...
,...
2211
22222121
11212111
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
(2.21)
Так как n
r
= , то определитель
nnnn
n
n
aaa
aaa
aaa
A
...
...
...
det
21
22221
11211
⋅⋅⋅⋅
= (2.22)
не равен 0.
Известно, что в этом случае система (2.21) имеет единственное
решение. Но если в этом решении хотя бы одна из переменных
njx
j
,1, =

64
отрицательна, тогда полученное решение ОЗЛП недопустимо и,
соответственно, ОЗЛП не имеет решения.
Если все njx
j
,1, = неотрицательны, то найденное решение является
допустимым и оптимальным для ОЗЛП, потому что других решений нет.
Этот тривиальный случай не интересует исследователей операций.
Мы будем исследовать случаи, когда n
r
<
, т.е. когда число
независимых уравнений, которым удовлетворяют переменные
njx
j
,1, = ,
меньше числа самих переменных. В случае, если система совместна,
существует бесчисленное множество решений. При этом mn
r
n
k
−
=−=
переменным можно давать произвольные значения, естественно, из
области их определения (
njx
j
,1,0 =≥ ). Эти
k
переменных называются
свободными. Остальные
k
nm
r
−
=
=
переменных выражаются через
свободные переменные и называются базисными.
2.4. Геометрическая интерпретация ОЗЛП
Пусть число свободных переменных n на два больше, чем
независимых уравнений m , которым они (свободные переменные) должны
удовлетворять, т.е. 2=− mn .
Тогда 2=
−
= mn
k
переменных выбираем в качестве свободных, а m
переменных сделаем базисными и выразим их через свободные. Получим
2−= nm уравнений вида
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++=
++=
++=
.
,
,
2211
42421414
32321313
nnnn
βxaxax
βxaxax
βxaxax
LLLLLLLLLL
(2.23)
Дадим ЗЛП геометрическую интерпретацию (рис. 2.1). По осям
21
0,0 xx
будем откладывать значения свободных переменных. Так как по
условию 0,0
21
≥≥ xx , то допустимые значения свободных переменных
располагаются в первом квадранте. Отметим это штриховкой,
обозначающей допустимую сторону каждой координатной оси.
Рис. 2.1. Геометрическая интерпретация ЗЛП

65
Базисные переменные
n
xxx ,......,,
43
также должны быть
неотрицательными, т.е.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥++=
≥++=
≥++=
.0
.......................................
,0
,0
2211
42421414
32321313
nnnn
βxaxax
βxaxax
βxaxax
(2.24)
Изобразим условия (2.21) геометрически. Рассмотрим одно из этих
условий, например
0
32321313
≥
+
+
=
β
xaxax . Положим, 0
3
=x . Тогда
0
3232131
=
++
β
xaxa . Это уравнение прямой линии в координатах
21
0xx
.
На этой прямой
0
3
=x (см. рис. 2.1). По одну сторону от прямой x
3
>0, по
другую x
3
<0 в зависимости от коэффициентов
3231
,aa и
3
β
. Отметим
штриховкой ту сторону от прямой
0
3
=
x , где x
3
> 0.
Пример 1
.20
,20
,2020
,2
12
21
12213
213
=→=
=→=
−=→=−−→=
−
−=
xx
xx
xxxxx
xxx
Пусть
0
21
== xx , 02002
3
>
=
−
−
=
x . Если 2;2
21
== xx , то
02222
3
<
−=−−=x .
Штриховка направлена вниз у линии
0
3
=
x
. Аналогично построим
прямые 0,......,0,0
54
=
==
n
xxx и отметим штриховкой допустимую
сторону, где соответствующая базисная переменная
mix
i
,1, =
больше
нуля. Таким образом, получено n прямых: две оси координат
0,0
21
=
= xx
и n–2 прямых (0,......,0,0
43
=
==
n
xxx ). Каждая из этих n прямых
определяет допустимую полуплоскость, лежащую по одну ее сторону.
Часть плоскости
21
0xx
, принадлежащая одновременно всем этим
полуплоскостям, образует область допустимых решений (ОДР).
Область допустимых решений ОЗЛП всегда представляет собой
выпуклый многоугольник (для n - m = 2). Выпуклой называется фигура
(многоугольник), которая обладает следующим свойством: если две точки
А и В отрезка АВ принадлежат этой фигуре, то и весь отрезок АВ
принадлежит ей.
На рис. 2.1 приведен
пример, когда ОДР ОЗЛП существует, т.е.
система уравнений-ограничений ОЗЛП имеет неотрицательные решения.
Но могут быть случаи, когда неотрицательных решений системы не
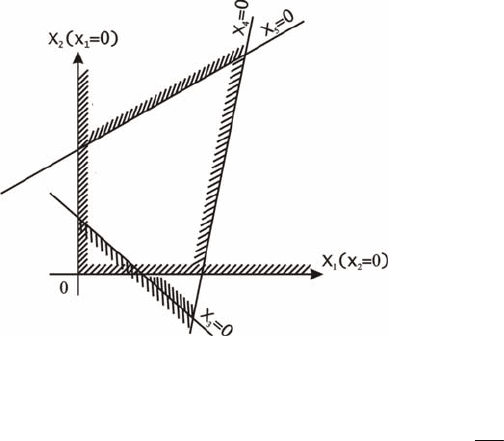
существует. Это означает, что не существует и ОДР (рис. 2.2).
66
Рис. 2.2. Геометрическая интерпретация ЗЛП, не имеющей решения
Пример 2
В задаче ЛП семь переменных
7,1,0 =≥ jx
j
. Имеется
5=m ограничений:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=+−−
=+
−=−+
−=−−−
=+−
.7222
,5
,4
,52
,4
3
7621
62
521
4321
21
xxxx
xx
xxx
xxxx
xxx
Требуется построить ОДР, если она существует.
Решение
Выберем в качестве свободных переменных
0,0
21
≥≥ xx и выразим
через них базисные переменные x
3
, x
4
, x
5
, x
6
, x
7
. Из первого уравнения
,4
213
++−= xxx третьего – 4
215
+
+
=
xxx , четвертого – 5
26
+−= xx .
Подставим во второе уравнение
4
213
+
+
−
=
xxx
. Имеем
,542
,5)4(2
42121
42121
−=−−−+−
−
=
−
+
+
−
−
−
xxxxx
xxxxx
123
214
+
−
=
xxx .
Подставим в пятое уравнение 5
26
+
−
=
xx . Имеем
,72522
,72)5(22
7221
7221
=+−+−
=
+
+
−
−
−
xxxx
xxxx
65,0
217
+
+
−
=
xxx
.
67
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−==
==
−−==
+==
−==
.122;0
,5;0
,4;0
,5,05,1;0
,4;0
127
26
125
124
123
xxx
xx
xxx
xxx
xxx
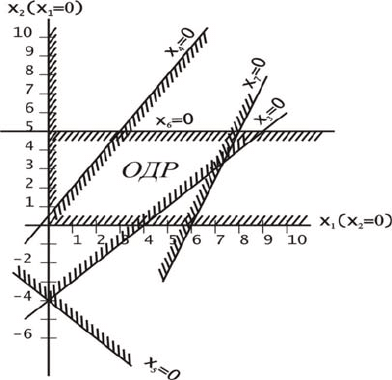
Для случая n – m = 2 оказалось возможным построить ОДР
(см. рис. 2.3).
Теперь рассмотрим вопрос о нахождении из числа допустимых
(предполагаем, что ОДР существует) оптимального решения, т.е. решения,
которое приводит в минимум линейную функцию
nn
xcxcxcW
+
+
+
= ...
2211
. (2.25)
Рассмотрим случай, когда n-m=2, и дадим геометрическую
интерпретацию поиску оптимального решения ОЗЛП. Положим, что
0,0
21
≥≥ xx – свободные переменные, а 0,...,0,0
43
≥≥≥
n
xxx – базисные
переменные. Подставим выражение для x
3
, x
4
,…, x
n
(2.24) в выражение для
W (2.25), приведем подобные члены и выразим как линейную функцию
только свободных переменных x
1
и x
2
.
Получим
22110
xxW
γ
γ
γ
+
+
=
, (2.26)
где
0
γ
– свободный член, которого в первоначальном виде у функции W не
было.
Рис. 2.3. Геометрическая интерпретация решения ЗЛП для примера 2
При переходе к выражению через свободные переменные x
1
и x
2
этот
свободный член мог появиться. Очевидно, что линейная функция (2.26)
достигает минимума при тех же значениях x
1
и x
2
, что и функция
2211
xxW
γ
γ
+=
′
, т.к.
0
γ
−=
′
WW
, где
0
γ
не зависит от x
1
и x
2
. Минимумы
функций
W и W
′
достигаются при одних и тех же значениях x
1
и x
2
и
отличаются друг от друга на величину
0
γ
.

68
Приравняем
W
′
к некоторой постоянной величине С:
2
1
2
1
22211
,
γ
C
x
γ
γ
xилиCxγxγW +−==+=
′
.
Это уравнение прямой линии в координатах
21
xx . Угловой
коэффициент этой прямой равен
2
1
γ
γ
− . Если изменить значение константы
С на С
1
, то угловой коэффициент прямой
1
CW
=
′
будет равен
2
1
γ
γ
− :
.
,
2
1
2
1
2
12211
γ
C
γ
γ
x
CxγxγW
+−=
=
+
=
′
При изменении С на С
1
прямая
W
′
перемещается параллельно самой
себе. Если положить, что
0
=
′
W (основная прямая), то при перемещении
этой прямой параллельно самой себе линейная функция
W
′
будет убывать
в одну сторону перемещения и, наоборот, возрастать в другую.
Построим основную прямую 0
=
′
W на плоскости
21
0xx . Угловой
коэффициент прямой равен
2
1
γ
γ
−
. Выясним, при перемещении в какую
сторону параллельно самой себе
W
′
убывает, т.е. движется в сторону
минимума.
Рассмотрим различные варианты.
1. Пусть
21
22 xxW +=
′
. Приравняем 0
=
′
W . Имеем
12
xx
−
= .
Направление убывания
W
′
показано стрелками (рис. 2.4) для случая γ
1
>0,
γ
2
>0.
Рис. 2.4. Расположение линии целевой функции
W при γ
1
>0, γ
2
>0
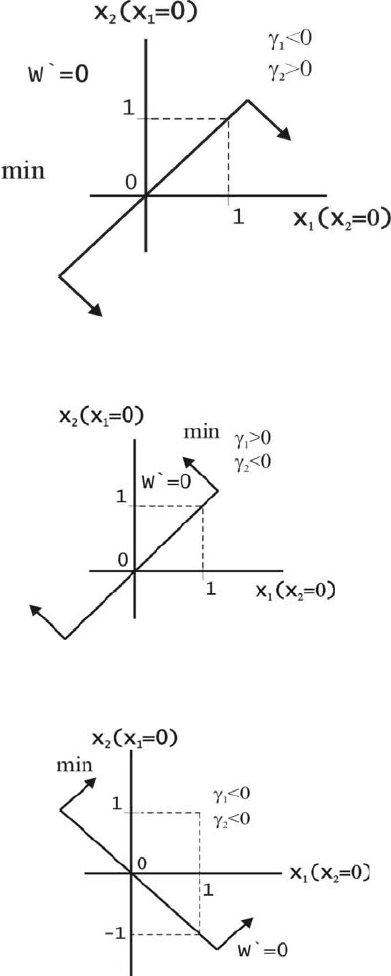
2. Пусть
21
22 xxW +−
=
′
для
12
0 xxW
=
→
=
′
(рис. 2.5).
69
Рис. 2.5. Расположение линии целевой функции
W при γ
1
<0, γ
2
>0
3. Пусть
21
22 xxW −
=
′
для
12
0 xxW
=
→
=
′
(рис. 2.6).
Рис. 2.6. Расположение линии целевой функции
W при γ
1
>0, γ
2
<0
4. Пусть
21
22 xxW −−
=
′
для
12
0 xxW
−
=
→
=
′
Рис. 2.7. Расположение линии целевой функции
W при γ
1
<0, γ
2
<0
Положение на плоскости
21
0xx основной прямой 0=
′
W и
направление убывания линейной формы
W
′
определяются величинами и
знаками коэффициентов
γ
1
и γ
2
при свободных переменных x
1
и x
2
в
выражении
W
′
.
Дадим геометрическую интерпретацию нахождения оптимального
решения ОЗЛП среди допустимых. Пусть имеется ОДР и основная прямая
0
=
′
W (рис. 2.8). Известно направление убывания линейной формы W
′
.
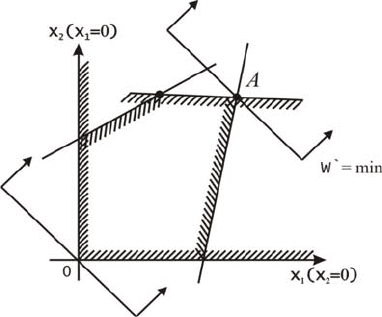
70
Рис. 2.8. Геометрическая интерпретация нахождения
оптимального решения ОЗЛП
При перемещении основной прямой в направлении, указанном
стрелками, линейная форма
W
′
будет убывать. Очевидно, что
наименьшего своего значения
W
′
достигнет, когда прямая
0
CW =
′
будет
проходит через наиболее удаленную от начала координат точку ОДР.
Координаты (в данном случае т. А)
0
1
х и
0
2
х определяют оптимальное
решение ОЗЛП. Зная оптимальные значения свободных переменных
0
1
х и
0
2
х и подставив их в уравнения, можно определить оптимальные значения
базисных переменных:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++=
++=
++=
,
.......................................
,
,
0
22
0
11
0
4
0
242
0
141
0
4
3
0
232
0
131
0
3
nnnn
βxaxax
βxaxax
βxaxax
,
а также оптимальное (в смысле минимума) значение линейной функции
W
′
:
0
22
0
110min
xxW
γγγ
++=
′
.
Пример 3
Найти оптимальное решение ОЗЛП для ограничений примера 2,
которое обращает в минимум линейную целевую функцию
7654321
232 xxxxxxxW
−
+
−
−
+−
=
. (2.27)
Решение
В примере 2 уравнения-ограничения были разрешены относительно
базисных переменных
x
3
, x
4
, x
5
, x
6
, x
7
, которые были выражены через
свободные переменные
x
1
и x
2
:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
++−=
+−=
++=
+−=
++−=
.65,0
,5
,4
,123
,4
217
26
215
214
213
xxx
xx
xxx
xxx
xxx
