Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

Homogeneous Coordinates andTransformations of the Plane 37

Exercise 2.26

Determine the modelling transformation matrices of the four instances

of Square which deﬁne the windows of the front of the house in Fig-

ure 1.8. Complete the picture element House by determining the mod-

elling transformation matrix of the primitive Point which is a small

circle centred at the point (0, 0). Now create a modern housing estate by

instancing House!

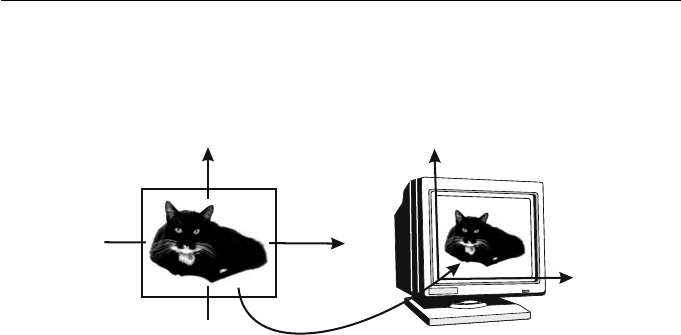
2.6.2 Device Coordinate Transformation

Sections 1.8.1 and 2.6.1 discuss how the model of an object is obtained by

instancing a number of picture elements and graphical primitives. The object

(the front of a house) is deﬁned in a two-dimensional world coordinate system.

The object is displayed in a device window, such as a computer screen, by

applying a device coordinate transformation. The process of viewing an object

deﬁned in a three-dimensional world coordinate system is discussed later in

Chapter 4.

Suppose the world coordinate system is the (x, y)-plane. The region of the

plane to be displayed by the device is speciﬁed by a rectangular window with

lower left corner (x

min

) and upper right corner (x

max

). Any part

of the object lying outside this region is “clipped” and is not displayed. The

coordinate system of a display device is determined by its resolution. For ex-

ample, a computer screen consists of a rectangular array of pixels. The number

of pixels in the horizontal (h) and vertical (v) directions is written h × v and

called the screen resolution. The origin is assumed to be the lower left cor-

ner of the screen, and the pixels are labelled with coordinates (h, v)whereh

and v are non-negative integers. Figure 2.6 illustrates a screen with a resolu-

tion of 1280 × 1024 pixels, and a window given by (x

min

)=(−10, −5)

and (x

max

) = (10, 5). The window is mapped onto the screen by the

device coordinate transformation which is the concatenation of (i) the transla-

tion T (10, 5) which maps the point (−10, −5) to the origin, and (ii) a scaling

S (1280/20, 1024/10) which makes the rectangle the same size as the screen.

Therefore, the device coordinate transformation is

T (10, 5) S (1280/20, 1024/10) =

⎛

⎝

100

010

10 5 1

⎞

⎠

⎛

⎝

6400

0 102.40

001

⎞

⎠

⎛

⎝

64 0 0

0 102.40

640 512 1

⎞

⎠

38 Applied Geometry for Computer Graphics and CAD

Hence the Cartesian coordinates of the point on the screen corresponding to

the point (x, y) in the window are (64x + 640, 102.4y + 512).

Device coordinate

transformation

-10

-5

Figure 2.6 A device coordinate transformation makes Max a ﬁlm star

Exercise 2.27

Suppose the window speciﬁed above is to be mapped onto a rectangular

device window of the computer screen with lower left corner (200, 200)

and upper right corner (600, 400). Determine the device coordinate trans-

formation matrix.

2.7 Point and Line Geometry in Homogeneous

Coordinates

The general equation of a line in the Cartesian plane is ax + by + c =0.

Suppose (X, Y, W) are the homogeneous coordinates of the point (x, y), so

that x = X/W and y = Y/W. Substituting for x and y in the equation of the

line, and multiplying through by W, yields the condition for (X, Y, W)tobea

point on the line

aX + bY + cW =0. (2.12)

The equation is known as the homogeneous line equation. The line is uniquely

deﬁned by the coeﬃcients a, b,andc, or any non-zero multiple ra, rb,andrc

of them. Therefore, it is natural to specify the line by the homogeneous line

coordinates

 =(a, b, c) .

Homogeneous Coordinates andTransformations of the Plane 39

It is also useful to consider  to be a vector known as the line vector .Since

any non-zero multiple of  deﬁnes the same line, only the direction of  is of

importance. Let P(X, Y, W) be a point on the line. By permitting the homo-

geneous coordinates (X, Y, W) to be treated as a vector, Equation (2.12) may

be expressed as the dot product

 · P = aX + bY + cW =0. (2.13)

The identity (2.13) leads to two useful operations: (i) determining the line

through two distinct points, and (ii) determining the point of intersection of

two lines.

To Find the Equation of the Line Through Two Points

Suppose  is the line vector of a line containing two distinct points

)andP

). Then (2.13) yields

 · P

=0 and  · P

=0.

For any two vectors, the condition a · b = 0 implies that a and b are perpen-

dicular. Hence,  is a vector perpendicular to both P

and P

. To determine 

it is suﬃcient to determine any vector perpendicular to P

and P

. In partic-

ular, the cross product gives a vector perpendicular to two given vectors, thus

 = P

× P

(or any multiple of P

× P

). Hence, the equation of the line

through two points can be determined by taking the “cross product” of the

homogeneous coordinates of the points.

Example 2.20

The line  passing through (0, 5) and (6, −7) satisﬁes

 · (0, 5, 1) = 0 and  · (6, −7, 1) = 0 .

Hence

 =(0, 5, 1) × (6, −7, 1) = (12, 6, −30)

giving the line 12x +6y − 30 = 0.

To Determine the Point of Intersection of Two Lines

Suppose P is the point of intersection of two lines 

and 

.ThenP is a point

on both lines and (2.13) yields



· P =0 and 

· P =0.

Hence P is a vector perpendicular to both 

and 

, and hence it is suﬃcient

to take P = 

× 

(or any multiple of it). The cross product yields the

homogeneous coordinates of the point of intersection.

40 Applied Geometry for Computer Graphics and CAD

Example 2.21

The point P of intersection of the lines x − 7y +8=0 and 3x − 4y +1=0

satisﬁes

(1, −7, 8) · P =0 and (3, −4, 1) · P =0.

Hence

P =(1, −7, 8) × (3, −4, 1) = (25, 23, 17) .

The Cartesian coordinates of the intersection point are (25/17, 23/17).

Example 2.22

The point P of intersection of the lines 2x − 5y =0and2x − 5y +3=0has

homogeneous coordinates

P =(2, −5, 0) × (2, −5, 3) = (−15, −6, 0) .

The point of intersection (−15, −6, 0) is a point at inﬁnity since the lines are

parallel.

EXERCISES

2.28. Determine the line passing through (1, 3) and (4, −2).

2.29. Determine the point of intersection of the lines x − 3y +7=0and

4x +3y − 5=0.

2.30. The methods used to determine the line through two distinct points

and the point of intersection of two lines both involve the cross prod-

uct. This is due to the duality between points and lines in the plane

which relates results about points and lines to a dual result about

lines and points. For example, the property “points r

, r

,andr

are collinear if and only if r

· (r

× r

) = 0” has the dual property

“lines 

, 

,and

are concurrent if and only if 

· (

× 

) = 0”.

Investigate further the property of duality [24, pp78–80].

Homogeneous Coordinates and

Transformations of Space

3.1 Homogeneous Coordinates

Homogeneous coordinates in three-dimensional space are derived in a similar

manner as homogeneous coordinates of the plane. A point (x, y, z) in three-

dimensional Cartesian space R

is represented in the four-dimensional space

by the vector (x, y, z, 1), or by any multiple (rx,ry, rz, r)(withr =0).

When W = 0, the homogeneous coordinates (X, Y, Z, W ) represent the Carte-

sian point (x, y, z)=(X/W, Y /W, Z/W ). A point of the form (X,Y, Z,0) does

not correspond to a Cartesian point, but represents the point at inﬁnity in the

direction of the three-dimensional vector (X, Y, Z). The set of all homogeneous

coordinates (X, Y, Z, W ) is called (three-dimensional) projective space and de-

noted P

. Homogeneous coordinates (x, y, z, w) are frequently represented by

the row matrix (xyzw) for matrix computations.

Example 3.1

The homogeneous coordinates (2, 3, 4, 5), (−4, −6, −8, −10), and (6, 9, 12, 15)

all represent the point with Cartesian coordinates (2/5, 3/5, 4/5).

42 Applied Geometry for Computer Graphics and CAD

Deﬁnition 3.2

A (projective) transformation of projective space is a mapping L : P

→ P

the form

L (x, y, z, w)=



xyzw



⎛

⎜

⎝

⎞

⎟

⎠

The 4×4 matrix M is called the homogeneous transformation matrix of L.IfM is

a non-singular matrix then L is called a non-singular transformation. If m

= m

=0and m

=0,thenL is said to be an aﬃne transformation.

(Aﬃne transformations correspond to translations, scalings, rotations etc. of

three-dimensional Cartesian space.)

3.2 Transformations of Space

A number of transformations of space are considered, namely, translations,

scalings, reﬂections, rotations, and the composition of these transformations.

As in the planar case, compositions of three-dimensional transformations are

performed by multiplication of the transformation matrices.

3.2.1 Translations

The transformation matrix of a translation by x

, y

,andz

units in the x-,

y-, and z-directions respectively, is

T (x

⎛

⎜

⎝

1000

0100

0010

⎞

⎟

⎠

The point with homogeneous coordinates P(x, y, z, 1) is translated to the point



given by



x + x

y + y

z + z





xyz1



⎛

⎜

⎝

1000

0100

0010

⎞

⎟

⎠

Hence, P(x, y, z) is transformed to P



(x + x

,y+ y

,z+ z

) as required.

3. Homogeneous Coordinates and Transformations of Space 43

3.2.2 Scalings and Reﬂections

A scaling about the origin by a factor s

, s

,ands

in the x-, y-, and

z-directions respectively, is obtained by the following transformation matrix

S (s

⎛

⎜

⎝

000

0 s

00s

000s

⎞

⎟

⎠

Frequently, s

is taken to be 1.

The transformation matrices of the reﬂections R

in the x = 0 plane, R

in the y = 0 plane, and R

in the z = 0 plane, are obtained by taking a scaling

of −1 in one of the coordinate directions,

⎛

⎜

⎝

−1000

0100

0010

0001

⎞

⎟

⎠

⎛

⎜

⎝

1000

0 −100

0010

0001

⎞

⎟

⎠

⎛

⎜

⎝

10 00

01 00

00−10

00 01

⎞

⎟

⎠

3.2.3 Rotations about the Coordinate Axes

Rotations in space take place about a line called the rotation axis. The rotations

about the three coordinate axes are called the primary rotations.

1. Rotation about the x-axis through an angle θ

Rot

(θ

⎛

⎜

⎝

10 00

0cosθ

sin θ

0 −sin θ

cos θ

00 01

⎞

⎟

⎠

44 Applied Geometry for Computer Graphics and CAD

2. Rotation about the y-axis through an angle θ

Rot

(θ

⎛

⎜

⎝

cos θ

0 −sin θ

0100

sin θ

0cosθ

0001

⎞

⎟

⎠

3. Rotation about the z-axis through an angle θ

Rot

(θ

⎛

⎜

⎝

cos θ

sin θ

−sin θ

cos θ

0010

0001

⎞

⎟

⎠

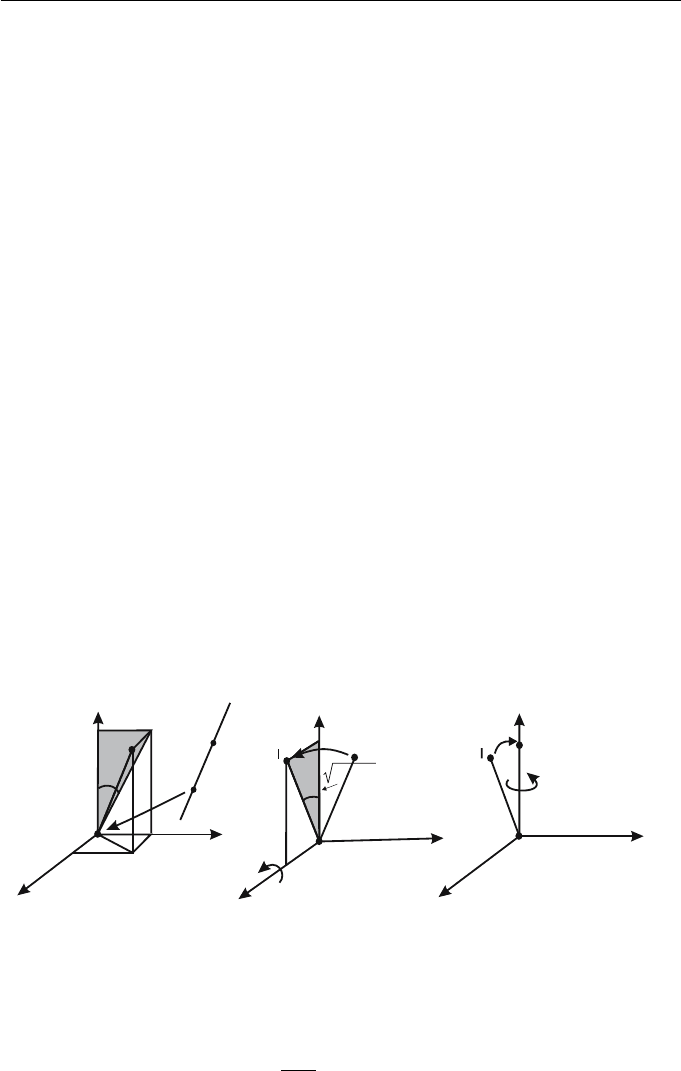
Figure 3.1 shows the directions which the primary rotations take when

the rotation angle is positive. The directions are easily remembered by the

mnemonic

For instance, to determine the positive sense of a rotation about the y-axis,

cover up the “y”torevealz → x. The arrow indicates that a positive angle

of rotation has the eﬀect of moving points on the z-axis towards the x-axis.

A two-dimensional rotation in the xy-plane about the origin yields the same

Figure 3.1 Deﬁnition of positive rotation angles

transformation of points in the plane as a three-dimensional rotation of the

plane about the z-axis. Rotations about an arbitrary line are obtained in Sec-

tion 3.2.4 by a composition of translations and primary rotations.

3. Homogeneous Coordinates and Transformations of Space 45

Example 3.3

The transformation matrix M which represents a rotation of an angle π/6

about the y-axis followed by a translation T (1, −1, 2) is

Rot

(π/6) T (1, −1, 2) =

⎛

⎜

⎝

0.866 0 −0.50

01.00 0

0.500.866 0

0001.0

⎞

⎟

⎠

⎛

⎜

⎝

1 000

0 100

0 010

1 −121

⎞

⎟

⎠

⎛

⎜

⎝

0.866 0 −0.50

01.000

0.500.866 0

1.0 −1.02.01.0

⎞

⎟

⎠

3.2.4 Rotation about an Arbitrary Line

Rotation through an angle θ about an arbitrary rotation axis is obtained by

transforming the rotation axis to one of the coordinate axes, applying a pri-

mary rotation through an angle θ about the coordinate axis, and applying the

transformation which maps the coordinate axis back to the rotation axis. Let

the rotation axis be the line through the points P(p

)andQ(q

Let R(r

) be the unit vector in the direction Q − P. Then the rotation

can be performed as follows.

-q-q

(a) (b) (c)

Figure 3.2

1. Apply the translation T (−p

, −p

) which maps P to the origin and

the rotation axis to the line

OR as shown in Figure 3.2(a). If R is parallel

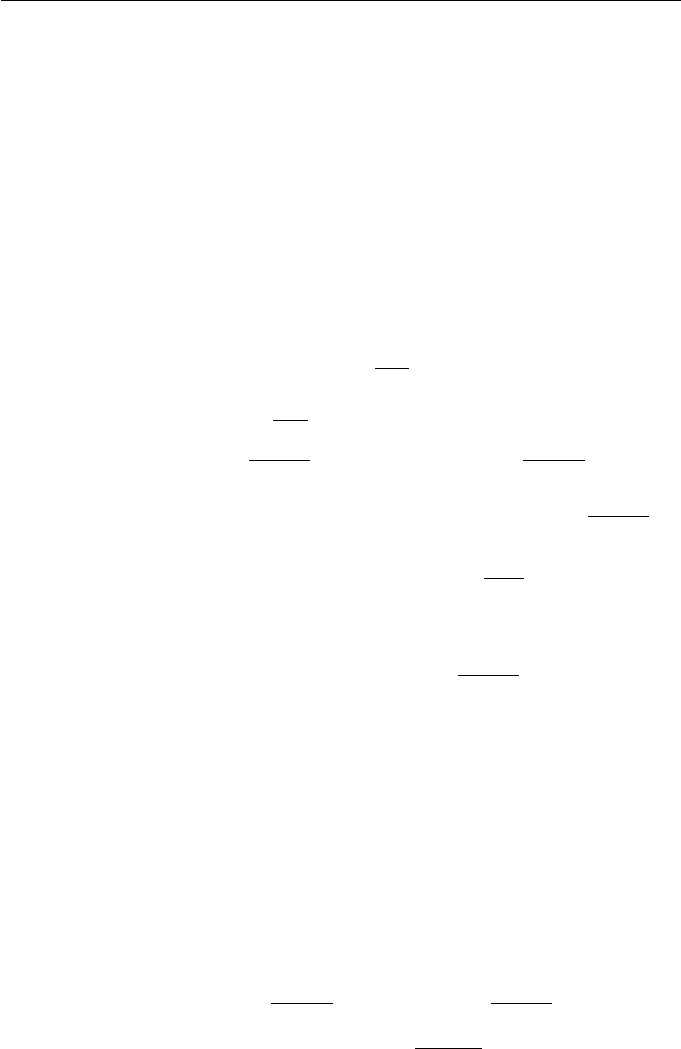
46 Applied Geometry for Computer Graphics and CAD

to the x-axis (when r

= r

= 0) then the required rotation matrix is

T (−p

, −p

) Rot

(θ) T (p

) .

Likewise, if R is parallel to the y-axis (when r

= r

=0)orthez-axis

(when r

= r

= 0) then the required rotation matrices are

T (−p

, −p

) Rot

(θ) T (p

)

T (−p

, −p

) Rot

(θ) T (p

)

respectively.

2. Suppose r

and r

are not both zero. Apply a rotation through an angle

about the x-axis so that the line OR is mapped into the xz-plane.

Referring to Figure 3.2(a), an application of trigonometry to the shaded

triangle yields that the line

OR makes an angle θ

with the xz-plane where

sin θ

= r



+ r

, and cos θ

= r



+ r

The desired rotation Rot

(θ

)mapsR to the point R



, 0,



+ r

)as

depicted in Figure 3.2(b).

3. Apply a rotation about the y-axis so that the line



is mapped to the

z-axis. Applying trigonometry to the shaded triangle of Figure 3.2(b) the

required angle is found to be −θ

where

sin θ

= r

, and cos θ



+ r

4. Apply a rotation through an angle θ about the z-axis (Figure 3.2(c)).

5. Apply the inverses of the transformations 1–3 in reverse order.

Thus the general rotation through an angle θ about the line through the points

P(p

)andQ(q

) has transformation matrix

T (−p

, −p

) Rot

(θ

) Rot

(−θ

) Rot

(θ) ×

Rot

(θ

) Rot

(−θ

)T (p

) ,

where R(r

) is the unit vector in the direction Q − P,and

sin θ

= r



+ r

, cos θ

= r



+ r

sin θ

= r

, and cos θ



+ r