Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.


Homogeneous Coordinates andTransformations of the Plane 27
-1
0
1
X
-1
0
1
Y
-1
0
1
W
Figure 2.4 Intersection of parallel lines on the spherical model of the
projective plane
2.4 Transformations in Homogeneous
Coordinates
In the following sections the homogeneous transformation matrices for transla-
tions, scalings, and rotations are described. In order to minimize on notation,
a transformation and its homogeneous transformation matrix will be given the
same notation. For instance, a translation and its translation matrix are both
denoted T (h, k).
2.4.1 Translations
The homogeneous translation matrix for the translation T (h, k)is
T (h, k)=
⎛
⎝
100
010
hk1
⎞
⎠
.
Then
xy1
⎛
⎝
100
010
hk1
⎞
⎠
=
x + hy+ k 1
,
verifying that the point (x, y) is translated to (x + h, y + k).
Example 2.10
In Example 1.8 the translation T (2, 1) was applied to the quadrilateral with
vertices A(1, 1), B(3, 1), C(2, 2), and D(1.5, 3). Let the homogeneous coordi-
nates of the 4 vertices be expressed as the rows of a 4×3 matrix. The translation
is applied by multiplying the matrix of vertices by the translation matrix. The

28 Applied Geometry for Computer Graphics and CAD
rows of the resulting matrix are the homogeneous coordinates of images of the
vertices.
⎛
⎜
⎜
⎝
111
311
221
1.531
⎞
⎟
⎟
⎠
⎛
⎝
100
010
211
⎞
⎠
=
⎛
⎜
⎜
⎝
321
521
431
3.541
⎞
⎟
⎟
⎠
.
vertices × translation = images of vertices
The images have Cartesian coordinates A
(3, 2), B
(5, 2), C
(4, 3), and
D
(3.5, 4).
2.4.2 Scaling about the Origin
The homogeneous scaling matrix is
S (s
x
,s
y
)=
⎛
⎝
s
x
00
0 s
y
0
001
⎞
⎠
.
Then
xy1
⎛
⎝
s
x
00
0 s
y
0
001
⎞
⎠
=
s
x
xs
y
y 1
,
verifying that the point (x, y, 1) is mapped to (s
x
x, s
y
y, 1). The scaling can also
be performed by the scaling matrix
S (s
x
,s
y
; s
w
)=
⎛
⎝
s
x
00
0 s
y
0
00s
w
⎞
⎠
for s
w
= 0. The transformation S (s
x
,s
y
; s
w
) represents a scaling about the
origin by a factor of s
x
/s
w
in the x-direction, and by a factor of s
y
/s
w
in the y-
direction. The semicolon before the s
w
is used to distinguish the planar scaling
from the spatial scaling which is introduced in Chapter 3.
Example 2.11
A scaling about the origin by a factor of 4 in the x-direction, and by a factor
of 2 in the y-direction, of the unit square with vertices (1, 1), (2, 1), (2, 2), and
(1, 2) is determined by
⎛
⎜
⎜
⎝
111
211
221
121
⎞
⎟
⎟
⎠
⎛
⎝
400
020
001
⎞
⎠
=
⎛
⎜
⎜
⎝
421
821
841
441
⎞
⎟
⎟
⎠
.

Homogeneous Coordinates andTransformations of the Plane 29
The image is a square with vertices (4, 2), (8, 2), (8, 4), and (4, 4).
2.4.3 Rotation about the Origin
In homogeneous coordinates the transformation matrix for a rotation Rot (θ)
about the origin through an angle θ is
Rot (θ)=
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
001
⎞
⎠
,
where a positive angle denotes an anticlockwise rotation. Hence
xy1
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
001
⎞
⎠
=
x cos θ − y sin θxsin θ + y cos θ 1
.
Example 2.12
An anticlockwise rotation about the origin through an angle π/3 of the unit
square with vertices (1, 1), (2, 1), (2, 2), and (1, 2) is determined by
⎛
⎜
⎜
⎝
111
211
221
121
⎞
⎟
⎟
⎠
⎛
⎝
0.50.866 0
−0.866 0.50
001.0
⎞
⎠
=
⎛
⎜
⎜
⎝
−0.366 1.366 1.0
0.134 2.232 1.0
−0.732 2.732 1.0
−1.232 1.866 1.0
⎞
⎟
⎟
⎠
.
The image is a square with vertices (−0.366, 1.366), (0.134, 2.232),
(−0.732, 2.732), and (−1.232, 1.866).
EXERCISES
2.10. Apply the translation T (−2, −1) to the quadrilateral, obtained in
Example 2.10, with vertices A
(3, 2), B
(5, 2), C
(4, 3), and D
(3.5, 4).
2.11. Write down the transformation matrix which has the effect of a
scaling by a factor of 2 in the x-direction and by a factor of 1.5
in the y-direction. Apply the transformation to the quadrilateral of
Example 2.10. Compare the result with Example 1.11.
2.12. Write down the transformation matrix which has the effect of an
anticlockwise rotation about the origin through an angle π/2. Apply
the transformation to the quadrilateral of Example 2.10.

30 Applied Geometry for Computer Graphics and CAD
2.13. Determine the matrix for the inverse scaling transformation of Ex-
ercise 2.11.
2.14. Determine the homogeneous transformation matrix of Rot (θ)
−1
.
2.15. Determine the homogeneous transformation matrices for reflections
in the x-andy-axes.
2.5 Concatenation of Transformations
In homogeneous coordinates, the concatenation of transformations T
1
and T
2
,
denoted T
1
◦ T
2
, can be performed with matrix multiplications alone. For ex-
ample, a rotation Rot (θ) about the origin followed by a translation T (h, k)is
denoted Rot (θ) ◦ T (h, k), and has the homogeneous transformation matrix
Rot (θ) T (h, k)=
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
001
⎞
⎠
⎛
⎝
100
010
hk1
⎞
⎠
=
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
hk1
⎞
⎠
.
Example 2.13
The transformation matrix which represents an anticlockwise rotation of 3π/2
about the origin followed by a scaling by a factor of 3 units in the x-direction
and 2 units in the y-direction is
Rot (3π/2) S (3, 2) =
⎛
⎝
0 −10
100
001
⎞
⎠
⎛
⎝
300
020
001
⎞
⎠
=
⎛
⎝
0 −20
300
001
⎞
⎠
.
EXERCISES
2.16. Determine the matrix which represents the operations of Example
2.13 performed in reverse order. What can be deduced about the
order in which transformations are performed?
2.17. Determine the matrix which represents an anticlockwise rotation
about the origin through an angle π followed by a scaling by a factor
of 4 in the x-direction and by a factor of 0.5inthey-direction.

Homogeneous Coordinates andTransformations of the Plane 31
2.18. Determine the matrix which represents a translation of 4 units in
the x-direction followed by a rotation about the point (2, 3) through
an angle π/2inaclockwise direction.
2.5.1 Inverse Transformations
The identity and inverse transformations were introduced in Section 1.2. The
identity transformation I is the transformation which has the effect of leaving
all points of the plane unchanged. The inverse of a transformation L, denoted
L
−1
, has the effect of mapping images of the transformation L back to their
original points. These transformations can be given a more precise definition
in terms of the concatenation of transformations.
Definition 2.14
The identity transformation of the plane, denoted I, is the transformation for
which I ◦L = L ◦ I = L, for all planar transformations L. The transformation
matrix of the identity transformation is the 3 × 3 identity matrix I
3
(that is,
the matrix with values of 1’s on the leading diagonal and 0’s elsewhere).
Definition 2.15
The inverse L
−1
of a transformation L is the transformation such that L◦L
−1
=
I and L
−1
◦ L = I.
Lemma 2.16
Let the homogeneous transformation matrix of L be T. A necessary and suf-
ficient condition for the inverse L
−1
to exist is that T
−1
exists and is the
transformation matrix of L
−1
.
Proof
Suppose L has an inverse L
−1
with transformation matrix T
1
. The concatena-
tion L ◦ L
−1
= I has transformation matrix TT
1
= I
3
. Similarly, L
−1
◦ L = I
has transformation matrix T
1
T=I
3
. Thus by the definition of a matrix inverse
T
1
=T
−1
.
Conversely, suppose T has an inverse T
−1
, and let L
1
be the transformation
defined by T
−1
.SinceTT
−1
= I
3
and T
−1
T=I
3
it follows that L ◦ L
1
= I
and L
1
◦ L = I. Hence L
1
is the inverse transformation of L.

32 Applied Geometry for Computer Graphics and CAD
Definition 2.17
A transformation L : P
2
→ P
2
which has an inverse L
−1
is called a non-singular
transformation. Lemma 2.16 shows that a transformation is a non-singular
transformation if and only if its transformation matrix is non-singular.
Example 2.18
Non-singular matrices A and B satisfy (AB)
−1
= B
−1
A
−1
.Further,S (s
1
,s
2
)
−1
= S (1/s
1
, 1/s
2
)andRot (θ)
−1
= Rot (−θ) (Exercises 1.9 and 1.14). This gives
a straightforward way of determining the inverse transformation matrix of the
concatenated transformation Rot (3π/2) ◦ S (3, 2):
(Rot (3π/2) S (3, 2))
−1
= S (3, 2)
−1
Rot (3π/2)
−1
= S (1/3, 1/2) Rot (−3π/2)
=
⎛
⎝
1
3
00
0
1
2
0
001
⎞
⎠
⎛
⎝
cos
−
3π
2
sin
−
3π
2
0
−sin
−
3π
2
cos
−
3π
2
0
001
⎞
⎠
=
⎛
⎝
0
1
3
0
−
1
2
00
001
⎞
⎠
.
Alternatively, using Example 2.13
(Rot (3π/2) S (3, 2))
−1
=
⎛
⎝
0 −20
300
001
⎞
⎠
−1
=
⎛
⎝
0
1
3
0
−
1
2
00
001
⎞
⎠
.
EXERCISES
2.19. Determine the transformation matrix of the inverse of the concate-
nation T (−2, 5) ◦ Rot (−π/3).
2.20. Use a graphics calculator or mathematics computer package to com-
pute the inverse of the transformation with matrix
⎛
⎝
1.00.50.0
0.8 −1.20.0
4.0 −2.01.0
⎞
⎠
.
2.21. Consider a (rectangular) Cartesian coordinate system with origin O
and coordinates (x, y), and a second system with origin O
(x
0
,y
0
)

Homogeneous Coordinates andTransformations of the Plane 33
and coordinates (x
,y
). The origin and axes of the first system can
be mapped to those of the second by applying a rotation Rot(θ)fol-
lowed by the translation T(x
0
,y
0
). The (x, y)-coordinates of a point
given in (x
,y
)-coordinates is obtained by applying the orthogonal
change of coordinates transformation
x = x
cos θ − y
sin θ + x
0
y = x
sin θ + y
cos θ + y
0
.
a) Determine the homogeneous transformation matrix A of the
change of coordinates and show that det(A)=1.
b) Determine the inverse change of coordinates transformation
which determines the (x
,y
)-coordinates of a point (x, y).
c) Show that a change of coordinates preserves the angle between
a pair of lines.
d) Show that the x
-andy
-axes, expressed in (x, y)-coordinates,
are given by the equations
(x − x
0
)sinθ − (y − y
0
)cosθ =0, and
(x − x
0
)cosθ +(y − y
0
)sinθ =0.
2.5.2 Rotation about an Arbitrary Point
A rotation through an angle θ about an arbitrary point (x
0
,y
0
) is obtained
by performing a translation which maps (x
0
,y
0
) to the origin, followed by a
rotation through an angle θ about the origin, and followed by a translation
which maps the origin to (x
0
,y
0
). The rotation matrix is
Rot
(x
0
,y
0
)
(θ)=T (−x
0
, −y
0
) Rot (θ) T (x
0
,y
0
)
=
⎛
⎝
100
010
−x
0
−y
0
1
⎞
⎠
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
001
⎞
⎠
⎛
⎝
100
010
x
0
y
0
1
⎞
⎠
=
⎛
⎜
⎜
⎝
cos θ sin θ 0
−sin θ cos θ 0
(−x
0
cos θ
+y
0
sin θ + x
0
)
(−x
0
sin θ
−y
0
cos θ + y
0
)
1
⎞
⎟
⎟
⎠
.
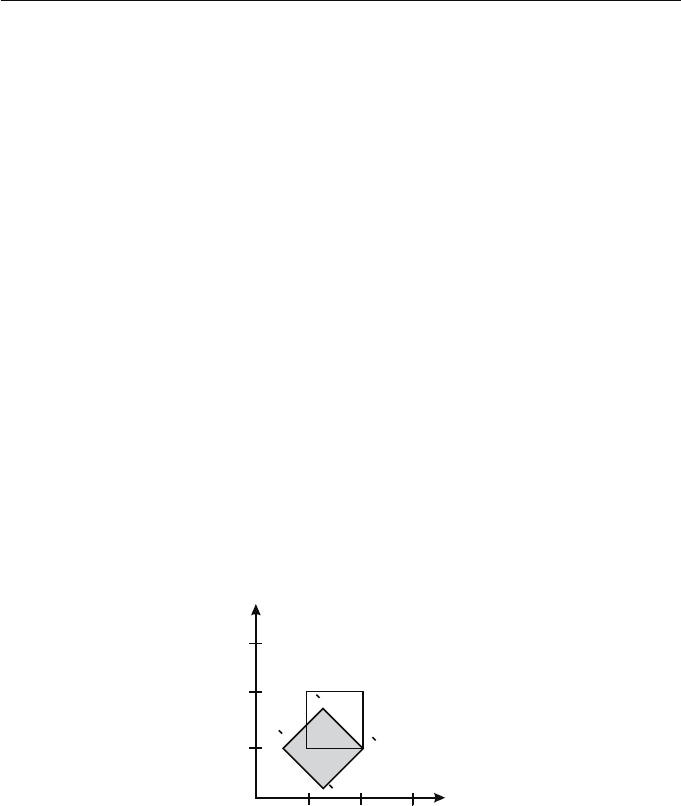
34 Applied Geometry for Computer Graphics and CAD
Example 2.19
A square has vertices A(1, 1), B(2, 1), C(2, 2), and D(1, 2). Calculate the coor-
dinates of the vertices when the rectangle is rotated about B through an angle
π/4. The required transformation is
T (−2, −1) Rot (π/4) T (2, 1)
=
⎛
⎝
100
010
−2 −11
⎞
⎠
⎛
⎝
0.7071 0.7071 0
−0.7071 0.7071 0
001
⎞
⎠
⎛
⎝
100
010
211
⎞
⎠
=
⎛
⎝
0.7071 0.7071 0
−0.7071 0.7071 0
1.2929 −1.1213 1
⎞
⎠
.
Applying the transformation to the vertices,
⎛
⎜
⎜
⎝
111
211
221
121
⎞
⎟
⎟
⎠
⎛
⎝
0.7071 0.7071 0
−0.7071 0.7071 0
1.2929 −1.1213 1
⎞
⎠
=
⎛
⎜
⎜
⎝
1.2929 0.2929 1
211
1.2929 1.7071 1
0.5858 1 1
⎞
⎟
⎟
⎠
gives A
(1.2929, 0.2929), B
(2, 1), C
(1.2929, 1.7071), and D
(0.5858, 1.0). The
rotated square is illustrated in Figure 2.5.
D
A
D
C
B
3
2
1
0
0123
0 1 2 3
AB
C
Figure 2.5
2.5.3 Reflection in an Arbitrary Line
Reflections in the x-andy-axes were derived in Exercise 2.15.A reflection in an
arbitrary line with equation ax + by + c = 0 is obtained by transforming the
line to one of the axes, reflecting in that axis, and then applying the inverse of
the first transformation. Suppose b =0.

Homogeneous Coordinates andTransformations of the Plane 35
1. The line intersects the y-axis in the point (0, −c/b).
2. Apply a translation mapping (0, −c/b) to the origin, and thus mapping
to a line
through the origin with an identical gradient to .
3. The gradient of
is tan θ = −a/b,whereθ is the angle that makes with
the x-axis. Rotate
about the origin through an angle −θ.Thelineisnow
mapped to the x-axis.
4. Apply a reflection in the x-axis.
5. Apply the inverse of the rotation of step 3, followed by the inverse of the
translation of step 2.
The concatenation of the above transformations is
⎛
⎝
10 0
01 0
0 c/b 1
⎞
⎠
⎛
⎝
cos θ −sin θ 0
sin θ cos θ 0
001
⎞
⎠
⎛
⎝
10 0
0 −10
00 1
⎞
⎠
×
⎛
⎝
cos θ sin θ 0
−sin θ cos θ 0
001
⎞
⎠
⎛
⎝
100
010
0 −c/b 1
⎞
⎠
(2.9)
=
⎛
⎝
cos
2
θ − sin
2
θ 2cosθ sin θ 0
2cosθ sin θ sin
2
θ − cos
2
θ 0
2
c
b
sin θ cos θ
c
b
sin
2
θ − cos
2
θ − 1
1
⎞
⎠
. (2.10)
Since tan θ =sinθ/ cos θ = −a/b, it follows that sin θ = a/
a
2
+ b
2
1/2
and cos θ = −b/
a
2
+ b
2
1/2
(Exercise 2.25). Hence, cos
2
θ = b
2
a
2
+ b
2
,
sin
2
θ = a
2
a
2
+ b
2
,sinθ cos θ = −ab
a
2
+ b
2
,andcos
2
θ − sin
2
θ =
b
2
− a
2
a
2
+ b
2
. Finally, substitution for the trigonometric functions in
(2.10) yields
⎛
⎜
⎝
b
2
−a
2
a
2
+b
2
−
2ab
a
2
+b
2
0
−
2ab
a
2
+b
2
−
b
2
−a
2
a
2
+b
2
0
−
2ac
a
2
+b
2
−
2bc
a
2
+b
2
1
⎞
⎟
⎠
.
Since in homogeneous coordinates multiplication by a factor does not affect
the result, the above matrix can be multiplied by a factor
a
2
+ b
2
to give the
general reflection matrix
R
(a,b,c)
=
⎛
⎝
b
2
− a
2
−2ab 0
−2ab −b
2
+ a
2
0
−2ac −2bc a
2
+ b
2
⎞
⎠
. (2.11)

36 Applied Geometry for Computer Graphics and CAD
EXERCISES
2.22. Show that the concatenation of two rotations, the first through
an angle θ about a point P(x
0
,y
0
) and the second about a point
Q(x
1
,y
1
) (distinct from P) through an angle −θ, is equivalent to a
translation.
2.23. Determine the transformation matrix of a reflection in the line 5x −
2y + 8 = 0. Express the reflection first using (2.11) and then as a
concatenation of transformations (2.9).
2.24. Demonstrate that if the coordinates of points are expressed by ra-
tional numbers (whole numbers and fractions), then a reflection in
a line defined by rational coefficients a, b, c can be computed using
integer arithmetic.
2.25. Use trigonometry to verify the result used in the derivation of
(2.11) that if tan θ = −a/b,thensinθ = a/
a
2
+ b
2
1/2
and
cos θ = −b/
a
2
+ b
2
1/2
.
2.6 Applications
2.6.1 Instancing
In Section 1.8.1 the model of the front of a house was defined by instancing
the picture element Square with vertices (0, 0), (1, 0), (1, 1), and (0, 1). The
front door was obtained by applying a scaling of 0.5 units in the x-direction,
followed by a translation of 3 units in the x-direction and 1 unit in the y-
direction. Transformations applied to picture elements and primitives to obtain
instances are called modelling transformations. The front door is obtained from
Square by applying the modelling transformation S(1, 3) ◦ T(4, 0) which has
the modelling transformation matrix
S(1, 3)T(4, 0) =
⎛
⎝
0.500
010
001
⎞
⎠
⎛
⎝
100
010
311
⎞
⎠
=
⎛
⎝
0.500
010
311
⎞
⎠
.
The vertices of the door are obtained by applying the modelling transformation
matrix to the vertices of the Square primitive, giving
⎛
⎜
⎜
⎝
001
101
111
011
⎞
⎟
⎟
⎠
⎛
⎝
100
010
311
⎞
⎠
=
⎛
⎜
⎜
⎝
311
411
421
321
⎞
⎟
⎟
⎠
.
So in world coordinates the vertices are (3, 1), (4, 1), (4, 2) and (3, 2).
