Marathe K. Topics in Physical Mathematics

Подождите немного. Документ загружается.

158 5 Characteristic Classes

Riemann–Roch–Hirzebruch (or RRH) theorem, which was itself an important

extension of the classical Riemann–Roch (or RR) theorem. This theorem

is now known as the Grothendieck–Riemann–Roch (GRR)theorem.

Grothendieck proved this theorem by using his new theory that he called K-

theory. When Hirzebruch asked Grothendieck to explain the signiﬁcance of

“K” in K-theory, Grothendiek replied: “ ‘H’ was already used for homology

and I did not like ‘I, J’, so I decided to call my theory K-theory.”

The starting point of Grothendieck’s proof is the construction of the

Grothendieck ring of the projective algebraic variety X.TheGrothendieck

ring K(X) is constructed with complex vector bundles and coherent sheaves

on X. Recall that a vector bundle corresponds to the locally free sheaf of its

sections. A coherent sheaf has a resolution in terms of vector bundles. This

allows a coherent sheaf S to be considered as an element of the ring K(X), as

an alternating sum of vector bundles. The deﬁnition of K(X) is based on the

notion of ring completion of a semi-ring. Recall that a semi-ring S satis-

ﬁes all the axioms of a ring except for the existence of the additive inverse.

If S has a unity then it is unique and is denoted by 1

or simply by 1. The

non-negative integers {0, 1,... } with the usual addition and multiplication

form a commutative semi-ring with unity (i.e., multiplicative identity). The

ring completion of the semi-ring N is the ring Z of all integers with the usual

addition and multiplication. In general, the ring completion of a semi-ring

S is a pair (



S,f), where



S is a ring and f : S →



S is a morphism of semi-

rings such that the following universal property is satisﬁed: If h : S → R is

any morphism of S into a ring R then there exists a unique ring morphism



h :



S → R such that



h ◦ f = h, i.e., the following diagram commutes:







We recall the construction of



S. Deﬁne the relation ∼ on S ×S by (a, b) ∼

(c, d)ifthereexistse ∈ S such that a + d + e = c + b + e.Itiseasytoverify

that this is an equivalence relation. We deﬁne



S := (S ×S)/∼ and denote by

[a, b] ∈



S the equivalence class of (a, b). Addition and multiplication in



S are

deﬁned by

[a, b]+[c, d]=[a + c, b + d],

[a, b] × [c, d]=[ac + bd, bc + ad].

We denote the class [0, 0] simply by 0 and deﬁne −[a, b]:

=[b, a]. We deﬁne

the map

f : S →



S by f(a)=[a, 0], ∀a ∈ S.

5.4 K-theory 159

It is customary to identify S with the image of f and to denote the class [a, 0]

simply by a and to denote [a, b]bya − b.

The following example is fundamental in our considerations.

Example 5.9 (The semi-ring Vect

(X)) Let X be any compact manifold

and F denote either of the ﬁelds R or C. Let Vect

(X) be the set of iso-

morphism classes of F -vector bundles over X. Then the set Vect

(X) has a

natural commutative semi-ring structure with unity, deﬁned by

1. the Whitney sum (α, β) → α ⊕ β as addition,

2. the tensor product (α, β) → α ⊗ β as multiplication,

3. θ

, the class of the trivial line bundle as unity,

where θ

∈ Vect

(X) denotes the isomorphism class of the trivial n-plane

bundle X × F

over X.

The Grothendieck ring K

(X) is deﬁned to be the ring completion of

the semi-ring Vect

(X). Thus elements of K

(X) can be written as A −

B, A, B ∈ Vect

(X). If V, W are vector bundles over X, then it is customary

to call [V ]−[W ]avirtual vector bundle and to denote it simply by V −W .

Now we recall that the Chern character Ch satisﬁes the following relations:

Ch(V ⊕ W )=Ch(V )+Ch(W ),Ch(V ⊗ W )=Ch(V ) Ch(W ), (5.41)

where V,W ∈ Vect

(X). Hence, Ch : Vect

(X) → H

∗

(X; R)isasemi-ring

morphism of Vect

(X) into the cohomology ring H

∗

(X; R) and hence lifts

to a unique ring morphism (also denoted by Ch) Ch : K

(X) → H

∗

(X; R)

deﬁned by

Ch([V ] −[W]) = Ch(V ) −Ch(W ). (5.42)

This morphism allows us to extend the deﬁnition of Chern character to vir-

tual vector bundles. In fact, the image of this morphism lies in the even

cohomology with rational coeﬃcients, i.e.,

Ch : K

(X) → H

even

(X; Q)=

∞



i=0

(X; Q) ⊂ H

∗

(X; R). (5.43)

In particular, if X is compact then the Chern character induces an isomor-

phism

(X) ⊗ Q

∼

even

(X; Q). (5.44)

In the case of spheres we can say more, namely,

)

∼

∗

; Z) ⊂ H

∗

; R). (5.45)

We note that in the original deﬁnition of K(X), the space X is a projective

algebraic variety. Thus a coherent sheaf S can be regarded as an element of

K(X) and the Chern character Ch(S) is well-deﬁned. Grothendieck then

deﬁnes the push forward of the sheaf S by an algebraic map f : X → Y of

160 5 Characteristic Classes

algebraic varieties, as a sheaf on Y . It is denoted by f

S. The GRR theorem

is then expressed by the formula;

∗

(Ch(S)τ(TX)) = Ch(f

S)τ(TY) , (5.46)

where f

∗

is the homomorphism on cohomology induced by the map f.Ifthe

space Y is a point then the GRR formula (5.46) reduces to the RRH formula.

The original RRH formula is in terms of a holomorphic vector bundle E over

a compact complex manifold X of complex dimension n.TheRRH formula

canbeexpressedasfollows:

(Ch(E)τ(TX))[X]=χ(X, E), (5.47)

where TX is the holomorphic tangent bundle of X,[X] is the fundamental

class of X,andχ(X, E)istheholomorphic Euler characteristic of E in

sheaf cohomology deﬁned by

χ(X, E):=

∞



i=0

(−1)

dim H

(X, E). (5.48)

The Chern character and the Todd class lie in the cohomology ring of X,

and evaluation on the fundamental homology class [X] is obtained from the

pairing of homology and cohomology (i.e., integration over X of the total class

in H

(X, E) in the expansion of Ch(E)τ(TX)). All the sheaf cohomology

spaces H

(X, E) are ﬁnite-dimensional. They equal zero for i>2n +1 so the

sum is ﬁnite. The RRH theorem, proved in 1954, provides the long sought

after generalization of the RR theorem from Riemann surfaces (i.e.r, complex

curves) to complex manifolds of arbitrary ﬁnite dimension. In fact, the RR

theorem in the current form was proved by Riemann’s student Gustav Roch,

improving on Riemann’s inequality in the 1850s. It provides an important tool

in the computation of the dimension of the space of meromorphic functions

on a compact connected Riemann surface Σ satisfying certain conditions. It

relates the complex analytic properties of Σ to its global topological prop-

erties, namely its Euler characteristic or, equivalently, its genus. The RRH

theorem is very much in the spirit of the RR theorem relating holomorphic

and topological data related to a ﬁxed variety. GRR theorem changes these

statements to a statement about morphism of varieties inaugurating the cat-

egorical approach which paved the way for K-theories for other structures.

These observations are useful in the study of index theorems for families of

elliptic operators such as the Dirac operator coupled to gauge ﬁelds.

We note that X → Vect

(X) deﬁnes a contravariant functor Vect

from the category of manifolds to the category of semi-rings. Simi-

larly, X → K

(X) deﬁnes a contravariant functor K

from the category of

manifolds to the category of rings. We recall that the F -rank of a vector

bundle over X is well deﬁned by the requirement of connectedness of X.

Therefore, the map

5.4 K-theory 161

ρ : Vect

(X) → Z, [α] → rank

(α),

is well deﬁned. It is easy to see that ρ is a morphism of semi-rings and

hence lifts to a ring morphism ρ : K

(X) → Z. We deﬁne the reduced

Grothendieck ring



(X)tobethekernelofρ, i.e.,



(X):=ker(ρ).

We denote by  : Z → K

(X) the map deﬁned by (1) := θ

and note

that ρ ◦  = id

. For a positive integer n, (n)=θ

=[X ×F

], the class of

the trivial n-plane bundle over X. One can show that the generic element of

(X)canbewrittenintheform[α] −θ

, [α] ∈ Vect

(X), and that

(X)

∼



(X) ⊕ Z. (5.49)

The contravariant functor K

can be used to give alternative deﬁnitions of the

maps ρ and  as follows: For a ∈ X,letι : {a}→X be the natural injection.

This induces a ring morphism K

(ι):K

(X) → K

({a}). Observing that

({a})

∼

Z, we can show that K

(ι) can be identiﬁed with ρ. Similarly,

we may identify  with K

(π), where π : X →{a} is the natural projection.

It is possible to deﬁne the ring



(X) directly by using the relation of

stable equivalence of vector bundles. We say that two vector bundles α, β

over X are stably equivalent or s-equivalent if there exist natural numbers

k, n such that

[α ⊕θ

]=[β ⊕ θ

] ∈ Vect

(X).

It can be shown that stable equivalence is an equivalence relation on

Vect

(X). Let us denote by E

(X)thesetofstable equivalence classes.

Under the operation induced by direct sum the set E

(X) is a group.

We observe that a generic element of



(X) can be written in the form

[α] − θ

r(α)

, [α] ∈ Vect

(X), where we have written r(α)forrank

(α). Let

[α]

denote the stable equivalence class of α.Themap

φ :



(X) → E

(X) deﬁned by [α] − θ

r(α)

→ [α]

is an isomorphism with inverse ψ : E

(X) →



(X) deﬁned by [α]

→

[α] −θ

r(α)

If Y is a closed subspace of X,wedenotebyX/Y the topological space

obtained from X by identifying Y to a point denoted by {y}.IfY = ∅,we

consider X/Y as obtained from X by adjoining a disjoint point, which we

also denote by {y}. Thus, in any case (X/Y, {y}) is a pointed topological

space. We deﬁne the relative K-group of X with respect to Y , denoted by

(X, Y ), to be the reduced K-group of X/Y , i.e.,

(X, Y ):=



(X/Y ).

162 5 Characteristic Classes

If Y = ∅ it follows that K

(X, ∅)

∼

(X). If X is locally compact we may

identify X/∅ with the one-point compactiﬁcation, denoted by X ∪{∞},of

X; in this case we deﬁne

(X):=K

(X/∅, {∞})=



(X/∅).

Thus, by deﬁnition,



We shall use the relative K-groups in the K-theoretic formulation of index

theorems later in this chapter.

If we consider only the group structure of K

(X)and



(X) then the

above considerations can be applied also to the case when F = H, the divi-

sion ring of quaternions. The functors



are usually denoted by



KO,



KU, and



KSp and are called the real, complex,andquaternionic

K-groups respectively. The reduced Grothendieck groups of S

, n>1, are

given by the following theorem.

Theorem 5.17 For n>1 we have the following group isomorphisms:



KO(S

)=π

n−1

(SO(∞)),



KU(S

)=π

n−1

(SU(∞)),



KSp(S

)=π

n−1

(Sp(∞)).

The following theorem is of fundamental importance in the K-theory treat-

ment of periodicity theorems.

Theorem 5.18 Let X be a compact manifold. Then in the complex case we

have the following isomorphism

KU(X) ⊗ KU(S

)

∼

KU(X × S

where KU(S

) is the free Abelian group on two generators 1 and η (the class

of the complex Hopf ﬁbration of S

over S

, which is the tautological complex

line bundle over CP

= S

). In the real case we have the isomorphism

KO(X) ⊗KO(S

)

∼

KO(X × S

where KO(S

) is the free Abelian group on two generators 1 and η

, the class

of the real 8-dimensional Hopf bundle (for further details see [198]).

The K-theory interpretation of the Bott periodicity theorem given below

is a direct consequence of the above two theorems.

Corollary 5.19



KO(S



KO(S

n+8



KU(S



KU(S

n+2

5.4 K-theory 163

It can be shown that the quaternionic K-groups are related to real K-

groups of spheres by the following relations:



KO(S



KSp(S

n+4

), (5.50)



KO(S

n+4



KSp(S

). (5.51)

These relations and Corollary 5.19 imply the following periodicity relation

for the quaternionic K-groups of spheres:



KSp(S



KSp(S

n+8

thus allowing us to calculate all the K-groups of spheres using the following

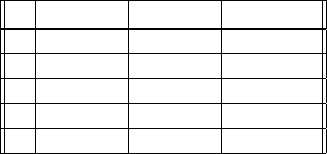
table.

Tab le 5. 1 Reduced Grothendieck groups of spheres



KO(S

)



KU(S

)



KSp(S

)

1 Z

0 0

2 Z

Z 0

3 0 0 0

4 Z Z Z

5 0 0 Z

We observe that these groups correspond to the stable homotopy groups

given in the Bott periodicity table in Chapter 2.

Grothendieck groups and rings have many interesting properties that par-

allel those of classical cohomology theories. For this reason K-theory is some-

times referred to as a generalized cohomology theory. Grothendieck’s ideas

were extended to the domain of topology, diﬀerential geometry, and algebra

by Atiyah, Hirzebruch, and other mathematicians. In topological K-theory

one associates to any compact topological space X, a group K(X) constructed

from the category of vector bundles on X.Inalgebraic K-theory one asso-

ciates to a ring R with unity the group K(R) constructed from the category

of ﬁnitely generated projective right R-modules. One of the main problems

in algebraic K-theory is the computation of K(R) for special classes of rings.

In diﬀerential geometry it is reasonable to think of K-theory as a generalized

cohomology theory that deals with classes of stable vector bundles. In this

case the set K(X) can be given the structure of a ring.

Applications of K-theory have provided new links and simpler proofs of

several important results in geometry, topology, and algebra. In particular,

as we discussed earlier, the Bott periodicity theorem can be interpreted as

atheoreminK-theory. J. F. Adams solved the long outstanding problem of

the existence of vector ﬁelds on spheres by using K-theory. Today K-theory

164 5 Characteristic Classes

has developed into an important discipline in its own right with its own

aforementioned journal K-Theory. A very readable account of K-theory may

be found in Karoubi [216].

5.5 Index Theorems

The Atiyah–Singer index theorem is one of the most important results of

modern mathematics. The theorem—or rather a set of theorems collectively

referred to as index theorems—were developed in a series of papers by Atiyah,

Singer and their collaborators. A good introduction to this and other related

results may be found in Gilkey [154], Lawson and Michelsohn [248], Palais

[311], and Shanahan [348]. Its application to gauge theories is discussed in the

book by Booss and Bleecker [47]. We give below a statement of some versions

of the index theorem and also consider special cases. Index theorems relate

analytic data of an operator on bundles over a manifold to the topological

data of these bundles. We discuss the relevant operator theory in Appendix D.

We also introduce below some additional machinery needed for the statements

of various index theorems.

1. If X and Y are compact spaces, one can deﬁne an outer product

⊗ of

X and Y ’s respective Grothendieck groups K(X)andK(Y ):

⊗ : K(X) × K(Y ) → K(X × Y )

such that [E]

⊗[F ]istheclassinK(X × Y ) determined by the vector

bundle E

⊗F over X ×Y with ﬁber E

⊗F

over (x, y). This product can

be extended to the case of locally compact spaces (see, for example, Booss

and Bleecker [47]).

2. Let E

and E

be vector bundles over the compact spaces X

and X

respectively, with A = X

∩ X

= ∅ and let X = X

∪ X

. Let f be

a vector bundle isomorphism of E

onto E

. We denote by E

∪

the vector bundle over X obtained by identifying the ﬁber E

,x∈ A,

with the ﬁber E

through the isomorphism f

.LetB

(resp., B

−

)denote

the upper (resp., lower) closed hemisphere of S

.ThusB

∩ B

−

= S

Consider the above construction with X

= B

−

= B

×C

(resp., E

= B

−

× C) the complex, trivial line bundle over B

(resp.,

−

), f : S

× C → S

× C the map deﬁned by f (z,z

)=z

/z.Let

−1

:= (B

× C) ∪

−

× C); then E

−1

is a vector bundle over S

.If

:= [S

× C] denotes the class of the trivial line bundle, the element

b := [E

−1

] − θ

is in the kernel of K(S

) → Z and thus b ∈ K(R

). The

class b is called the Bott class.LetX be a locally compact space; the Bott

periodicity theorem (complex case) asserts that the map m

: K(X) →

K(X ×S

) deﬁned by outer product by b, i.e., m

(u):=u

⊗b, u ∈ K(X),

is an isomorphism.

5.5 Index Theorems 165

3. Let E

and E

be vector bundles over X and let A be a closed subspace of

X.Letf be a vector bundle isomorphism of E

onto E

. Associated with

thetriple(E

; f ) there is a unique, canonically constructed element in

K(X, A). Let X

= X ×{1}, X

= X ×{2},andZ be the union of X

and

with (x, 1) and (x, 2) identiﬁed for all x ∈ A.Letπ

: Z → X

,r=1, 2

be the natural maps, and W = π

∗

∪

∗

.Letj : X

→ Z be the

natural injection. One can show that [W ] −[π

∗

]isinthekernelofK(j)

and thus can be considered an element of K(Z, X

). We now observe that

Z with X

reduced to a point can be identiﬁed with X in which A is

reduced to a point. Thus, K(Z, X

)

∼

K(X, A) and hence [W ] − [π

∗

]

can be identiﬁed with an element of K(X, A), which we denote [f]

4. Let E,F be two vector bundles over a compact Riemannian manifold M

and let P ∈ El

(E,F) be an elliptic operator of order k from Γ (E)to

Γ (F ). Deﬁne the disk bundle DM := {u ∈ T

∗

M |u≤1}. Apply-

ing the above construction to the triple (π

∗

(E),π

∗

(F ); σ

(P )), we have

[σ

(P )]

∈ K(DM, ∂DM). But DM/∂DM is naturally homeomorphic

to the one-point compactiﬁcation of T

∗

M and by means of the Rie-

mannian metric we may identify T

∗

M with TM. Thus we may consider

[σ

(P )]

∈ K(TM).

5. Recall that every m-dimensional compact manifold M can be trivially

embeddedinsomeR

m+n

in the following sense. The restriction of T R

m+n

to M allows one to deﬁne the normal bundle of M with ﬁbers N

such

that T

m+n

= T

M ⊕ N

. For large enough n the normal bundle is

trivial and in this case we say that M is trivially embedded in R

m+n

Furthermore, by choosing a trivialization we can write N = M ×R

. Thus

N becomes a tubular neighborhood of M in R

m+n

and TN = TM×R

Thus, an element a ∈ K(TM×R

) may be identiﬁed with an element in

K(R

2m+2n

) also denoted by a. Thus applying m+n times the inverse m

−1

of m

to a gives an element of Z, i.e., m

−(m+n)

(a) ∈ Z if a ∈ K(TM×R

We can now state the K-theoretic version of the index theorem.

Theorem 5.20 (Atiyah–Singer) Let M be a closed, oriented, Riemannian

manifold of dimension m, which is trivially embedded in R

m+n

.LetE and

F be Hermitian vector bundles over M and P ∈ El

(E,F) be an elliptic

operator of order k from Γ (E) to Γ (F ).Then

Ind(P )=(−1)

−(m+n)

([σ

(P )]

⊗b

). (5.52)

The cohomological versions of the Atiyah–Singer index theorem are ob-

tained by lifting to K(M) certain characteristic classes. One form is the

following.

Theorem 5.21 (Atiyah–Singer) Let M be a compact manifold of dimension

m and let P ∈ El

(E,F) be an elliptic operator of order k from Γ (E) to

Γ (F ). Then the index of P is given by

166 5 Characteristic Classes

Ind(P )=(−1)

{ch[σ(P )] · τ(TM ⊗ C)}[TM], (5.53)

where τ is the Todd class and [TM] is the fundamental class of the tangent

bundle.

We note that one can always roll up an elliptic complex to obtain a unique

elliptic operator with the same index. However, sometimes it is advantageous

to consider the full complex. A formulation of the index theorem for diﬀer-

ential complexes is the following.

Theorem 5.22 (Atiyah-Singer) Let M be a compact manifold of dimension

m and let (E,L) be an elliptic diﬀerential complex over M. Then there exists

a compactly supported cohomology class a(E, L) ∈ H

∗

(TM,Q) such that

Ind(E,L)=(a(E,L) ·τ(TM ⊗ C))([TM]), (5.54)

where τ is the Todd class and [TM] is the fundamental class of the tangent

bundle.

The statement of the index theorem takes a much simpler form in the

special case when all the Laplacians of the elliptic complex are second order

operators. In this case it can be shown that there exists a cohomology class

b(E,L) ∈ H

(M) with the property that

Ind(E,L)=(b(E,L))([M]).

Furthermore, b(E,L)=0foroddm. Hence, m odd implies that Ind(E,L)=

0. The index theorems for classical elliptic complexes are special cases of this

formula, as indicated below.

As we discussed earlier, for the de Rham complex we have E

= Λ

, L =

d,andb(E, L) = Euler class of M, and the index theorem takes the form

Ind(E,L)=χ(M), the Euler characteristic of M.

We now consider in detail the Hirzebruch signature operator D

and state

the relation of its index to the Hirzebruch signature of M.LetM be a com-

pact, oriented Riemannian manifold of dimension 4n. We deﬁne the involution

operator j : Λ

→ Λ

4n−k

α → j(α)=i

k(k−1)+2n

∗ α =(−1)

k(k−1)

∗ α.

The operator j extends to Λ and satisﬁes j

=1.WedenotebyΛ

(resp., Λ

−

)

the eigenspace of j for the eigenvalue +1 (resp., −1). Deﬁne D

= d + δ|

Then

: Λ

→ Λ

−

is an elliptic operator called the Hirzebruch signature operator.Wenow

deﬁne the Hirzebruch signature σ(M )ofM. Consider the bilinear operator

h : H

× H

→ R

5.5 Index Theorems 167

deﬁned by

(α, β) →



(α ∧β).

In the above formula we have used (α∧β) to denote the cohomology class and

a2n-form representing that class. We note that h is the intersection form on

M as deﬁned in Chapter 2. Let (e

−

) be the signature of the intersection

form h. Then the Hirzebruch signature is deﬁned by

σ(M)=e

− e

−

Let us denote by Δ

(resp., Δ

−

) the Laplacian on Λ

(resp., Λ

−

). If H

(resp., H

−

) denotes the space of harmonic 2n-forms in Λ

(resp. Λ

−

), then

one can show that

σ(M)=dimH

− dim H

−

Ind(D

)=dimkerΔ

− dim ker Δ

−

=dimH

− dim H

−

Hence,

Ind(D

)=σ(M).

We observe that σ(M) could be deﬁned in a purely topological way through

the cup product, because



(α ∧β)=([α] ∪ [β])([M ]).

A deeper result is the Hirzebruch signature theorem,whichgives

Ind(D



= L

[M],

where L

is the top degree form of the Hirzebruch L-polynomial. This result

can be obtained as a special case of the cohomological version of the Atiyah–

Singer index theorem.

A similar formulation can be given for the Dolbeault complex of a complex

manifold and the spin complex of a spin manifold.