Макушев Ю.П., Ширлин И.И. Динамика двигателей внутреннего сгорания

Подождите немного. Документ загружается.

где µ – масштаб площади суммарной диаграммы крутящего мо-

мента, Нм/м

⋅

⋅⋅=

µµµ

, (2.6)

где

180

= – масштаб, определяющий сколько радиан содер-

жится в абсциссе длиной в 1 м;

– масштаб, показывающий, сколько паскалей (Н/м

) содер-

жит ордината длиной в 1 м;

R – радиус кривошипа, м;

D – диаметр цилиндра, м.

По формуле (2.5) определяют L

изб

, а по формуле (2.2) J

. В расчетах

можно принять, что момент инерции маховика

CPM

RmJ

⋅

=⋅=

. (2.7)

Момент инерции маховика, его масса и средний радиус связаны вы-

ражением

)9,075,0( JJ

. (2.8)

Для автотракторных двигателей D

СР

= 0,3÷0,5 м.

Для приближенных расчетов можно принять

)32(

−

, (2.9)

где S – ход поршня, м.

Величина D

СР

зависит от габаритных

размеров двигателя, размеров муфты сцеп-

ления, стартерного венца. Определив D

СР

, по

формуле (2.7) находят массу маховика.

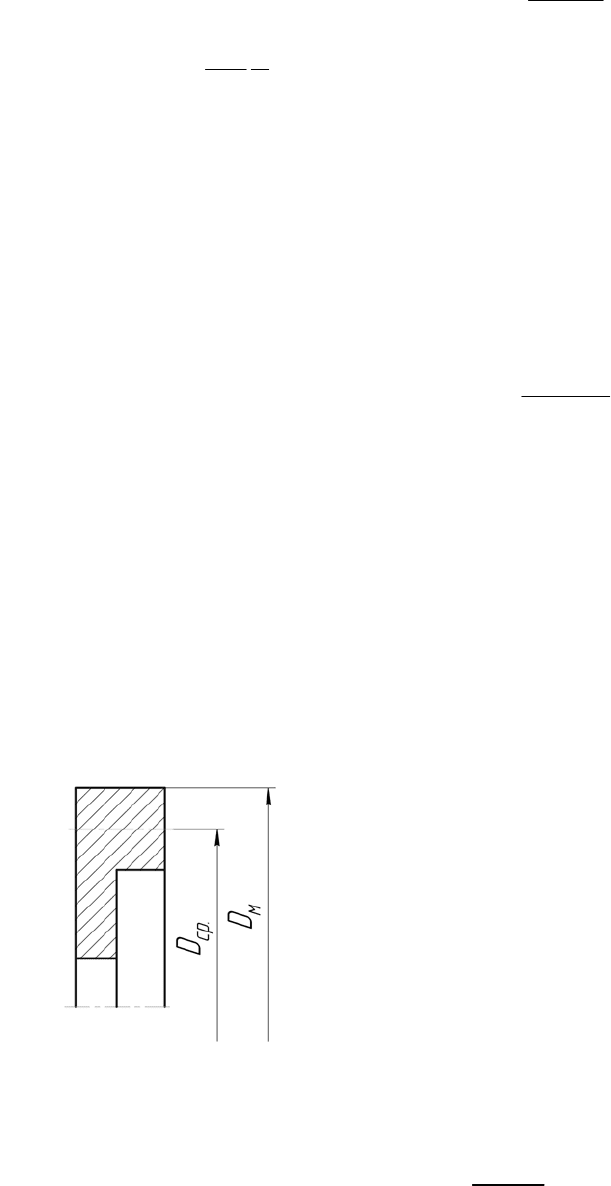
На рис. 2.4 показан маховик двигателя.

По условиям прочности внешний диаметр

маховика D

должен быть выбран с учетом

обеспечения допустимых окружных скоро-

стей.

Окружная скорость на внешнем обходе

маховика

. (2.10)

Рис. 2.4. Маховик двигателя

Окружная скорость для чугунных маховиков должна быть меньше

40…50 м/с, для стальных – меньше 60…70 м/с.

2.4. Пример расчета маховика

Предположим, что вы уже построили график суммарно крутящего

момента, например, для дизеля 4Ч13/14.

Известно, что l = 0,09 м; F

изб max

= 12·10

-4

; γ=180

Определим по формуле (2.6) масштаб суммарной диаграммы крутяще-

го момента:

мН

1065

13,014,3

07,0102

09,0

180

14,3 ⋅

⋅=

⋅

⋅⋅⋅⋅⋅=

По формуле (2.5) определим набольшую избыточную работу:

78010651012

изб

=⋅⋅⋅=

−

мН

⋅

Задаваясь значением δ=0,01 и определив:

183

175014,3

СР

⋅

−

находим по формуле (2.2) момент инерции всех движущихся масс двигате-

ля:

3,2

18301,0

780

⋅

мкг

⋅

Момент инерции маховика находим по формуле (2.7):

84,13,28,0

⋅

мкг

⋅

Принимая D

С Р

= 0,35 м, определим массу маховика:

35,0

84,14

⋅

СР

кг.

Принимая D

= 0,4 м и материал маховика – сталь, по формуле (2.10)

находим окружную скорость:

3,36

17504,014,3

⋅

v .м/с

Окружная скорость не превышает допустимых значений.

2.5. Порядок выполнения работы

1. Изучить методику расчета маховика.

В соответствии с заданием и по данным теплового и динамического

расчетов двигателя на ЭВМ произвести расчет маховика, определить

его массу и размеры.

2.6. Содержание отчета

Отчет должен содержать наименование и цель работы, краткое описа-

ние методики расчета маховика, расчет маховика для конкретного двига-

теля с учетом задания, необходимые графики и таблицы.

Контрольные вопросы

1. Назначение маховика.

Что называют коэффициентом неравномерности хода?

Как определяют момент инерции маховика?

Как определяется начальная фаза в цилиндре двигателя?

Как определяется наибольшая избыточная работа по диаграмме на-

бегающего момента?

Как определяют масштаб площади суммарной диаграммы крутящего

момента?

3 ПРИМЕНЕНИЕ ВЕКТОРНЫХ ДИАГРАММ В РАСЧЕТАХ ДВС

3.1. Цель и задачи работы

Изучить методику построения векторных диаграмм, сил, действую-

щих на шатунную шейку и подшипник коленчатого вала, освоить порядок

расчёта подшипников скольжения.

3.2. Вводная часть

Данная работа может быть использована как пособие по организации

самостоятельной аудиторной работы студентов специальности «Двигатели

внутреннего сгорания».

Векторные диаграммы [1,2] позволяют определить величину и на-

правление силы, действующей при каждом положении кривошипа на его

шейку или подшипник. Векторные диаграммы дают представление о на-

груженности шейки или подшипника, позволяют найти менее нагружен-

ную часть, где выбирают место сверления каналов для подвода масла.

Кроме того, при помощи векторных диаграмм производят расчёт подшип-

ников скольжения, строят диаграммы износа шейки и подшипника.

Векторные диаграммы строят после определения сил, действующих на

детали КШМ. На шейку действует три силы:

К – сила, направленная по оси кривошипа;

Т – касательная сила, перпендикулярная силе К;

RШ

– центробежная сила от вращающейся части шатуна.

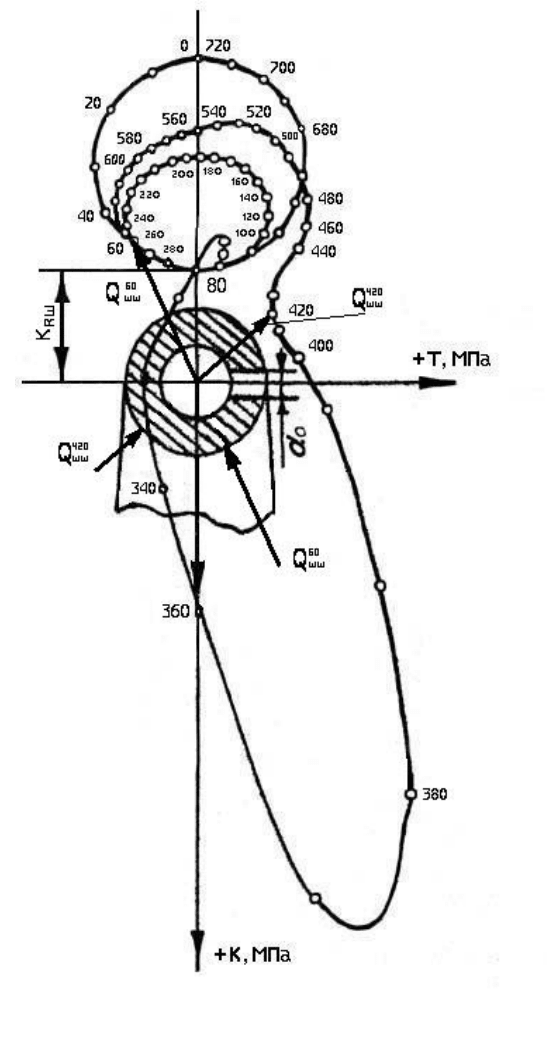
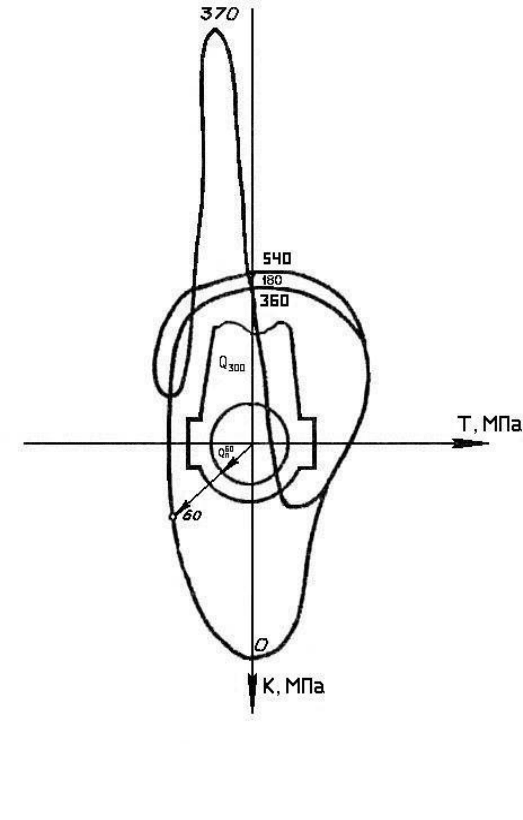
Векторную диаграмму сил, действующих на шейку, удобно строить

без учёта К

RШ

, постоянной по величине и направлению, учитывая её затем

соответствующим

сдвигом начала координат.

3.3. Векторная диаграмма сил, действующих на шатунную шейку

Для построения векторной диаграммы проводим оси координат. Вер-

тикальная ось (ось цилиндра) является осью сил К. Направление оси вниз

примем за положительное. Горизонтальная ось является осью сил Т. Её на-

правление вправо принимаем за положительное.

Для каждого положения кривошипа, начиная от

и до конца

цикла, берём из таблицы динамического расчёта двигателя значения сил Т

К, откладывая их на осях в выбранном масштабе с учётом знака. Из кон-

цов векторов проводим перпендикуляры. Каждую точку пересечения этих

перпендикуляров отмечаем соответствующим углом поворота кривошипа.

Полученные точки являются концами векторов, представляющих по вели-

чине и направлению равнодействующие силы для каждого угла поворота

кривошипа. Соединяя плавной кривой построенные точки, получим

век-

торную диаграмму сил, действующих на шатунную шейку без учёта

RШ

(рис. 3.1). Первоначальное положение оси

Т на рис. 3.1 показано штрихо-

вой линией.

Для учёта влияния

RШ

переносим начало координат по оси вниз на

величину, вычисленную по формуле

RШ

µω

⋅⋅⋅=

−62

, (3.1)

где

– масса вращательно движущейся части шатуна, кг;

R – радиус кривошипа, м;

⋅

– угловая скорость вращения коленчатого вала, с

-1

;

n – частота вращения коленчатого вала двигателя, мин

-1

;

– площадь поршня, м

;

– масштаб удельных сил.

Следует помнить, что в динамических расчётах для удобства все дей-

ствующие силы в КШМ относят к единице площади поршня. Данный под-

ход обоснован тем, что

давление газов в цилиндре

двигателя имеет величину

ньютон, деленный на метр

в квадрате (Н/м

). При

этом силы инерции должны

иметь такую же единицу

величины. Масштаб

за-

висит от выбранного раз-

мера векторной диаграммы.

Например, удельная сила в

1 МПа (1·10

Н/м

) может

соответствовать 20…40 мм.

Векторы, соединяю-

щие новое начало коорди-

нат с точками на векторной

диаграмме, выражают по

величине и направлению

силы, действующей на

шейку для каждого угла

поворота кривошипа. Сила

приложена к поверхности

шейки в точке пересечения

окружности шейки с лини-

ей действия вектора (точка

входа). На рис. 3.1 для

примера

построен вектор,

соответствующий углу по-

ворота кривошипа, равному

420º.

В менее нагруженной

части поверхности шейки

на основе конструкторских

и технологических соображений сверлится канал для подвода масла к

подшипнику. Диаметр отверстия следует выбирать в зависимости от диа-

метра шейки:

шшo

dd 08,0≥

. (3.2)

После построения векторной диаграммы сил, действующих на криво-

Рис. 3.1. Векторная диаграмма сил, действующих на

шатунную шейку

шипную шейку коленчатого вала, строят векторную диаграмму сил, дейст-

вующих на кривошипный подшипник шатуна.

3.4. Векторная диаграмма сил, действующих на подшипник шатуна

Силы, действующие на кривошипный подшипник шатуна, по величи-

не равны силам, действующим на кривошипную шейку, но противополож-

ны по направлению.

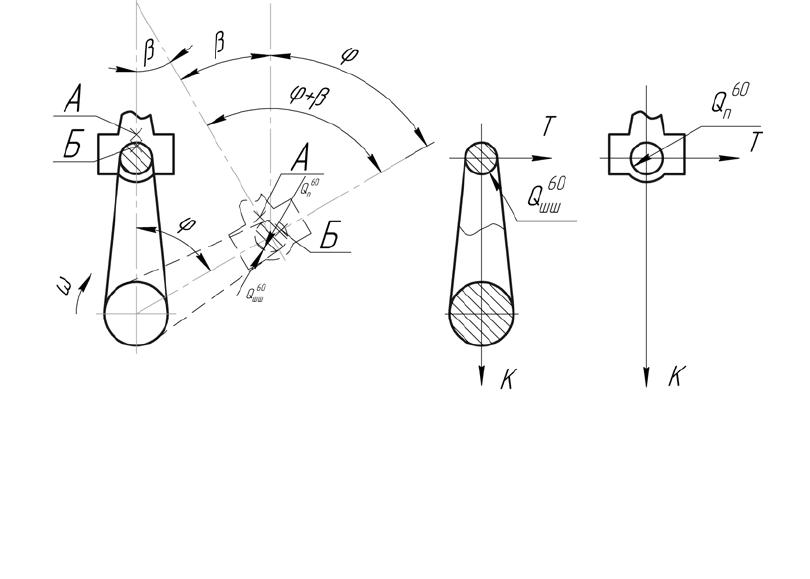
При повороте кривошипа, а следовательно, и кривошипной шейки на

угол

(рис. 3.2), подшипник шатуна повернётся относительно шейки в

противоположном направлении на угол

. Точка А на подшипнике пе-

ремещается противоположно направлению вращения относительно точки

Б на кривошипе.

Следовательно, чтобы правильно расположить вектор, действующий

при повороте кривошипа, относительно осей, соединённых с подшипником

шатуна, вектор надо повернуть в направлении, противоположном враще-

нию шейки, на угол

+ и направить в противоположную сторону.

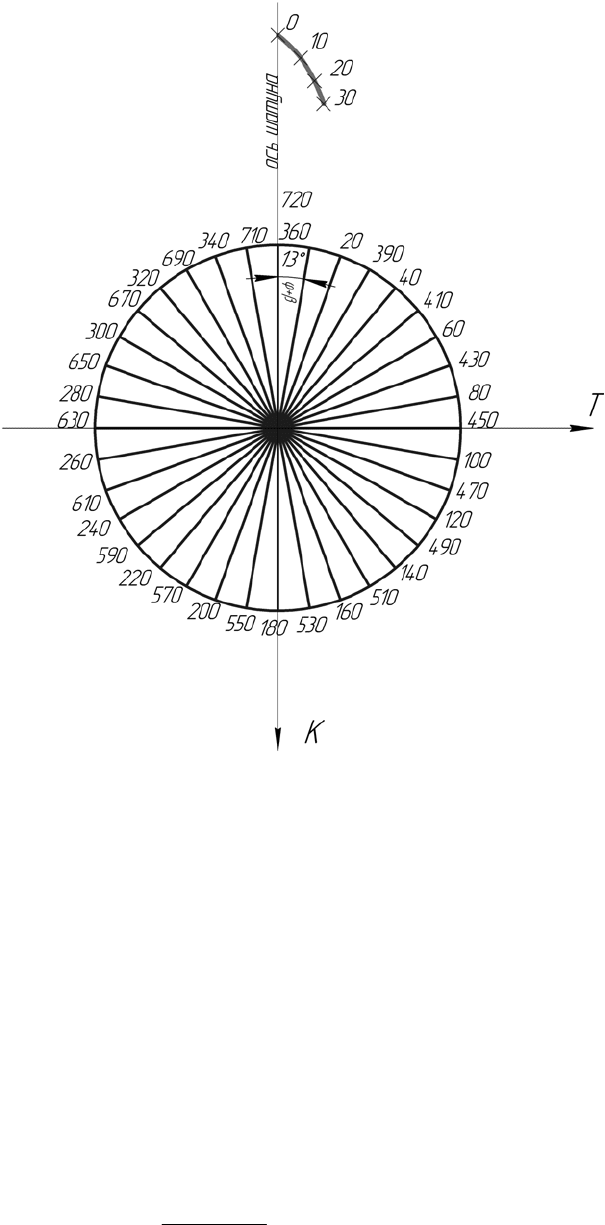
Для получения векторной диаграммы сил, действующих на криво-

шипный подшипник, берут лист кальки, проводят ось шатуна, откуда про-

ходит ось Т. Из центра проводят окружность произвольного радиуса.

У точки пересечения с осью шатуна (сверху) ставят цифры 0; 360

;

720

для четырёхтактных и 0; 360

– для двухтактных двигателей.

Рис. 3.2. Расположение силы,

действующей на шатунную шейку

и подшипник при повороте

коленчатого вала двигателя на угол

φ = 60°

Рис. 3.3. Расположение сил,

действующих на шатунную шейку

и подшипник относительно оси

силы К

Далее откладывают на окружности величину дуги φ+β. Значение β

для различных значений φ и λ даны в работе [2, с. 312].

Концы дуг обозначают величиной

φ. Например, φ = 10

; β = 3, откла-

дываем 13

, а пишем 10

; φ = 20

; β = 5

, откладываем 25

, а пишем 20

и т.

д. После этого кальку нужно наложить на векторную диаграмму сил, дей-

ствующих на кривошипную шейку так, чтобы при совмещённых началах

координат ось шатуна совпадала с осью

К.

Вращая кальку в направлении, противоположном движению криво-

шипа, совмещаем с осью

К последовательно все деления шкал и при каж-

дом положении отмечаем на кальке точки конца соответствующего векто-

ра диаграммы сил, действующих на шатунную шейку. Точки обозначаем

соответствующим углом

Внешний вид диаграмм

на подшипник (рис. 3.4) и на

шатунную шейку будет абсо-

лютно разный. Для объясне-

ния возьмём положение кри-

вошипа с шатуном при

= 60

(см. рис. 3.4). Точка приложе-

ния силы

Q на шейку и под-

шипник показана на схеме.

Рассмотрим действие силы

отдельно на кривошипную

шейку и подшипник в коор-

динатах

Т – К (рис 3.5). На-

правление силы на шейку и

подшипник не совпадают, чем

и объясняется различие по

виду векторных диаграмм.

После построения век-

торной диаграммы на шатун-

ный подшипник, её переносят

на лист, правильно располо-

жив относительно подшипни-

ка (см. рис 3.3). Для проверки

правильности построения

векторной диаграммы на ша-

тунный подшипник, возьмём,

например,

= 360

. В этом случае векторы силы Q, как для шатунной

шейки, так и для подшипника, должны лежать на оси

К, должны быть рав-

ны друг другу, но иметь противоположное направление (см. рис. 3.1 и 3.3

вектор

360

Рис. 3.4. Векторная диаграмма сил,

действ

ющих на подшипник

Наименее нагруженная часть кривошипного подшипника находится

на векторной диаграмме там, куда направлены из центра наименьшие по

величине векторы и наоборот.

Характер измене-

ния нагрузки на под-

шипник становится бо-

лее наглядным, если

векторную диаграмму

сил

Q перестроить в

прямоугольные коор-

динаты

Q –

(рис.

3.6). При построении

диаграммы все векторы

считаются положи-

тельными. Концы от-

ложенных векторов со-

единяют плавной кри-

вой.

Развёрнутая диа-

грамма сил, действую-

щих на подшипник,

аналогична развёрну-

той диаграмме сил,

действующих на ша-

тунную шейку.

Для дальнейших

расчётов коленчатого

вала и подшипников

скольжения определя-

ем

ср

и Q

мах

. Необхо-

димо помнить, что векторные диаграммы и развёрнутые диаграммы по-

строены с учётом масштаба и в удельных единицах.

3.5. Расчет подшипников скольжения

Большинство современных подшипников скольжения (вкладышей)

выполнены из стали и антифрикционного сплава. Толщина стальной ленты

0,9…3 мм, антифрикционного слоя 0,25…0,7 мм. Антифрикционный мате-

риал выбирают с учётом значения максимальных

max

, средних q

, удель-

ных давлений на подшипник и окружной скорости скольжения

⋅

max

, (3.3)

Рис. 3.5. Способ построения векторной диа-

граммы на шатунный подшипник

где d и

– диаметр и длина подшипника, м;

ncp

⋅

= ; (3.4)

⋅

. (3.5)

Для определения d и l необходимо знать длину и диаметр шатунной

шейки.

Для карбюраторных двигателей

шш

= (0,55 … 0,7)·D; (3.6)

шш

= (0,45 … 1)·d

шш

. (3.7)

Для дизелей

шш

= (0,63 … 0,75)·D; (3.8)

шш

= (0,73 … 1)·d

шш

(3.9)

где D – диметр цилиндра, м.

Диаметр подшипника равен диаметру шейки. Рабочая длина подшип-

ника может быть равна длине шейки или меньше, если имеется канавка в

подшипнике.

В табл. 3.1 приведены размеры шатунных и коренных шеек ряда оте-

чественных двигателей [4].

Рис. 3.6. Развернутая диаграмма сил, действующих на

шатунную шейку

Таблица 3.1

Размеры шеек коленчатых валов

Шатунная шейка Коренная шейка

Марка двигателя

d, мм l, мм d, мм l, мм

АЗЛК-412

52 21,5 60 25,5

ВАЗ-2101

47,8 25 5,8 22,5

ЗМЗ-53

60 23,5 70 24

ЗИЛ-130

65,5 27 74,5 26

ЯМЗ-236

88 34,2 110 40

КамАЗ-740

80 28 95 28

Д-240

68,25 38 75,25 32

СМД-60

85 34 92 40

В табл. 3.2 приведены средние и максимальные удельные давления на

шейках коленчатого вала.

Таблица 3.2

Удельные давления на шейках вала

Двигатели Подшипники

ср

, МПа q

max

, МПа

Шатунные 0,5-0,8 0,8-12

1. Автомобильные

Коренные 0,4-0,7 0,6-0,9

Шатунные 0,25-0,35 0,8-12

2. Тракторные

Коренные 0,35-0,4 0,6-0,9

Шатунные 0,9-16 25-42

3. Дизели форсированные

Коренные 10-17 20-30

Отношение

max

для шатунных и коренных шеек не должно превы-

шать 2 … 3.

Определив

max

и V , по табл. 3.3 выбираем материал антифрикцион-

ного сплава.

Таблица 3.3

Выбор антифрикционного сплава для подшипников скольжения

Материал

max

, МПа

V, м/с

Применяются на двига-

телях

1. Высокооловянистый баббит

Б-83

18-20 4-6, ГАЗ-51, М-20

2. Свинцовистая бронза Бр-30 24-35 10 ЯМЗ-236,238,240

3. Алюминиево-сурьмянисто-

магниевый сплав АСМ

20 9 СМД-17,14,60

4. Сплав АО-30 28 10 ЗИЛ-130,АЗЛК-412