Макушев Ю.П., Ширлин И.И. Динамика двигателей внутреннего сгорания
Подождите немного. Документ загружается.

10
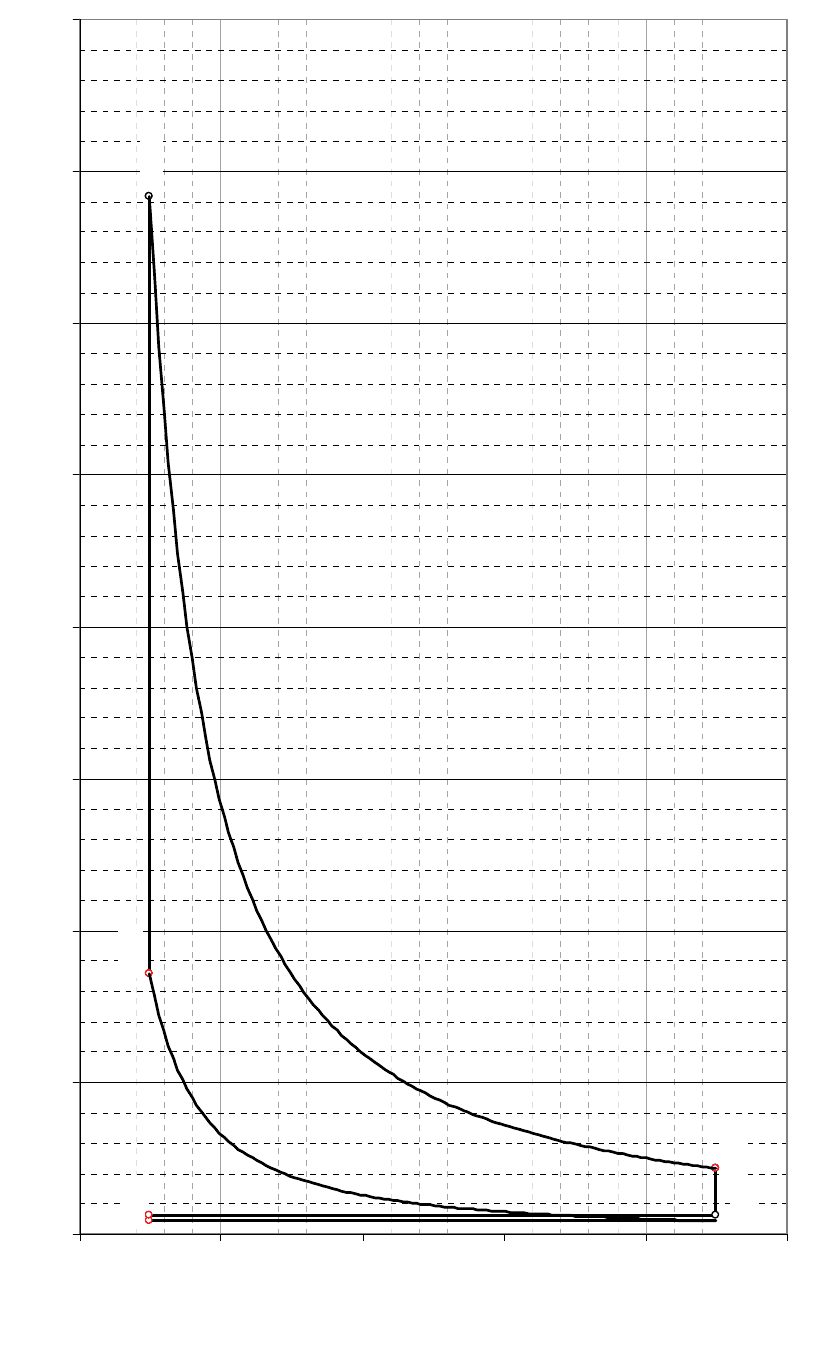
Рис. 1.4. Расчетная индикаторная диаграмма
c
z
a
b
r
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
0,000 0,100 0,200 0,300 0,400 0,500
Объем цилиндра, дм
3
Давление в цилиндре, МПа

11
Продолжение табл. 1.3.
1 2 3 4 5 6
330 0,85999 0,75999 -1,34916 -0,58918 0,325
360 1,71840 1,6184 -1,69515 -0,07674 0
360 6,73114 6,63114 -1,69515 4,936 0
390 3,57791 3,47791 -1,34916 2,12875 1,174
420 1,47840 1,3784 -0,5228 0,8556 0,785
450 0,80315 0,70315 0,32478 1,02793 1,028
480 0,55588 0,45588 0,84757 1,30346 1,062
510 0,45873 0,35873 1,02439 1,38311 0,621
540 0,43240 0,3324 1,04559 1,37799 0
540 0,12765 0,02765 1,04559 1,07324 0
570 0,12765 0,02765 1,02439 1,05203 -0,472
600 0,12765 0,02765 0,84757 0,87522 -0,713
630 0,12765 0,02765 0,32478 0,35242 -0,352
660 0,12765 0,02765 -0,5228 -0,49515 0,454
690 0,12765 0,02765 -1,34916 -1,32152 0,729
720 0,12765 0,02765 -1,69515 -1,6675 0
1.4. Определение сил инерции поступательно движущихся масс
Для определения инерционных сил, которые возникают при работе
двигателя, необходимо определить массу движущихся деталей. Для расче-
тов обычно используют массы деталей, приведенные к площади поршня.
Приведенную массу деталей выбирают на основе данных по аналогичным
деталям подобных двигателей.
В нашем случае примем удельную массу 113
'
=
n
m кг/м
2
, удельную
массу шатуна 180
'
=
ш
m кг/м
2
, а удельную массу неуравновешенных час-
тей одного колена вала без противовесов
180
'
=
к
m
кг/м
2
.
На основе принятых данных определим значение инерционных сил,
действующих на поршневой палец:
'6
10
jj
mjp ⋅−=
−
, (1.9)
где 162180275,0113275,0
'''
=⋅+=+=
шnj
mmm – удельная масса де-
талей
КШМ, совершающих возвратно-поступательные движения при
работе двигателя, кг/м
2
.
Изменение инерционных сил в зависимости от угла поворота колен-

12
чатого вала двигателя пропорционально ускорению поршня.
Из графика изменения ускорения поршня видно, что его числовое
значение изменяется в пределах от 0…180 град, поворота коленчатого вала.
Следовательно, изменение силы инерции в течение рабочего цикла доста-
точно определить только в этом интервале.
Разобьем данный интервал с шагом расчета 30 град и определим зна-
чения инерционной силы в этих точках от поступательно движущихся
масс:
– при
ϕ
= 0:
(
)
(
)
()()
;МПа69515,1
180275,011302cos237,00cos0255,057610
275,02coscos1010
26
''26'6
−=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=30:
(
)
(
)
()()
;МПа34916,1
180275,0113302cos237,030cos0255,057610
275,02coscos1010
26
''26'6
−=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=60:
(
)
(
)
()()
;МПа5228,0
180275,0113602cos237,060cos0255,057610
275,02coscos1010
26
''26'6
−=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=90:
(
)
(
)
()()
;МПа32478,0
180275,0113902cos237,090cos0255,057610
275,02coscos1010
26
''26'6
=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=120:
(
)
(
)
()()
;МПа84757,0
180275,01131202cos237,0120cos0255,057610
275,02coscos1010
26
''26'6
=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=150:
(
)
(
)
()()
;МПа02439,1
180275,01131502cos237,0150cos0255,057610
275,02coscos1010
26
''26'6
=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
– при
ϕ
=180:

13
(
)
(
)
()()
.МПа04559,1
180275,01131802cos237,0180cos0255,057610
275,02coscos1010
26
''26'6
=
=⋅+⋅⋅⋅+⋅⋅⋅−=
=⋅+⋅⋅+⋅⋅⋅−=−=
−
−−
шnjj
mmRjmp
ϕλϕω
Значения инерционной силы повторяются. Остальные значения инер-
ционных сил представлены в табл. 1.3.
Центробежная сила инерции от вращающихся масс нижней части ша-
туна определяется по формуле:
411,510959,5750255,063967,010
3232
.
−=⋅⋅⋅−=⋅⋅⋅−=
−−
ω
RmK
кшRш
кН,
где 63967,08823,0725,0725,0
.
=
⋅
=⋅=
шкш
mm – масса шатуна, со-
средоточенная на оси кривошипа, кг.
Центробежная сила инерции от вращающихся масс кривошипа опре-
делим по формуле:
46345,710959,5750255,08823,010
3232
−=⋅⋅⋅−=⋅⋅⋅−=
−
−
ω
RmK
к
шR
кН,
где
8823,00049,0180
'
=⋅=⋅=
nкк
Fmm
– масса неуравновешенных
частей одного колена вала без противовесов, кг.
Центробежная сила инерции вращающихся масс, действующая на
кривошип, равна сумме центробежных сил инерции:
8744,12411,546345,7
−
=
−
−
=
+
=
∑
шRкRR
KKK
кН.
1.5. Определение суммарной силы
Суммарная сила сосредоточена в центре поршневого пальца и опреде-
ляется из выражения
jг
PPP
+
∆
=
. (1.10)
Значения суммарной силы, полученные по формуле (1.10), сведены в
табл. 1.3.
По данным табл. 1.3 сроится диаграмма суммарной силы, действующей
в центре поршневого пальца.
1.6. Определение сил, действующих в деталях КШМ
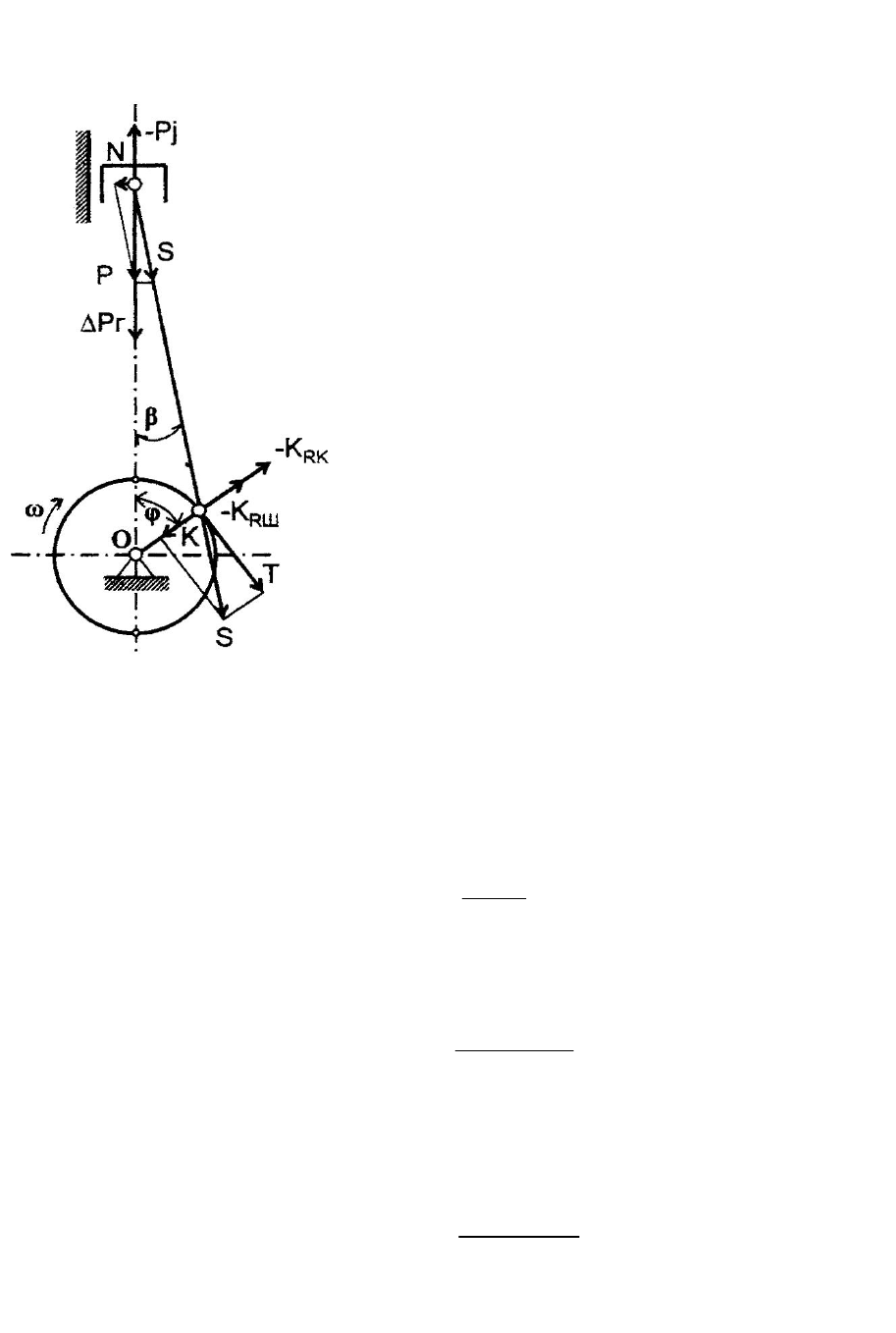
На рис. 1.5 показаны силы, действующие в КШМ. В результате алгеб-
раического сложения сил инерции от поступательно движущихся масс
j
P
и избыточного давления газов
г
P
∆
получим суммарную или движущую
14
силу
0
P
.
Сила
P
приложена в центр поршневого пальца и раскладывается на
боковую N, действующую на зеркало цилиндра; по шатуну S, сжимающую
и разрывающую шатун.
Сила S, перенесения в центр шатунной
шейки, раскладывается на тангенциальную Т,
создающую крутящий момент и силу K, дей-
ствующую по кривошипу.
Силы инерции от возвратно-
поступательно движущихся масс
3
10
−
⋅⋅−= jmP
jj
, (1.11)
где
j
m
– масса возвратно-
поступательно движущихся деталей, кг;
j – ускорение (замедление) возвратно-
поступательного движения, м/с
2
.
Причем для 4-тактных ДВС за цикл зна-
чения функции j(φ) повторяются дважды:
j(φ+360° )=j(φ).
Боковая (нормальная) сила давления
поршня на стенку цилиндра
(рис. 1.5)
β
tg
⋅
=
P
N
. (1.12)
Сила, действующая вдоль шатуна
β
cos
Р
S =
. (1.13)
Радиальная сила, действующая по оси кривошипа:
(
)
β
β
ϕ
cos
cos
+
⋅= PK
. (1.14)
Для определения тангенциальной силы, действующей по касательной
к шатунной шейке коленчатого вала, используют выражение:
(
)
β
βϕ
cos
sin +
⋅= PT
, (1.15)
где
β
– угол отклонения шатуна, относительно оси цилиндра.
Рис 1.5. Схема сил,
действующих в деталях КШМ
15
Для удобства определения тангенциальной силы, можно использовать
приближенное выражение, в котором угол
β
заменен выражением, связан-
ным с углом поворота коленчатого вала
ϕ
⎟
⎠
⎞
⎜
⎝
⎛
⋅+⋅=
ϕ
λ
ϕ
2sin
2
sinPT
. (1.16)
На основе представленного уравнения определим значения тангенци-
альной силы. Результаты расчета сведены в табл. 1.3.
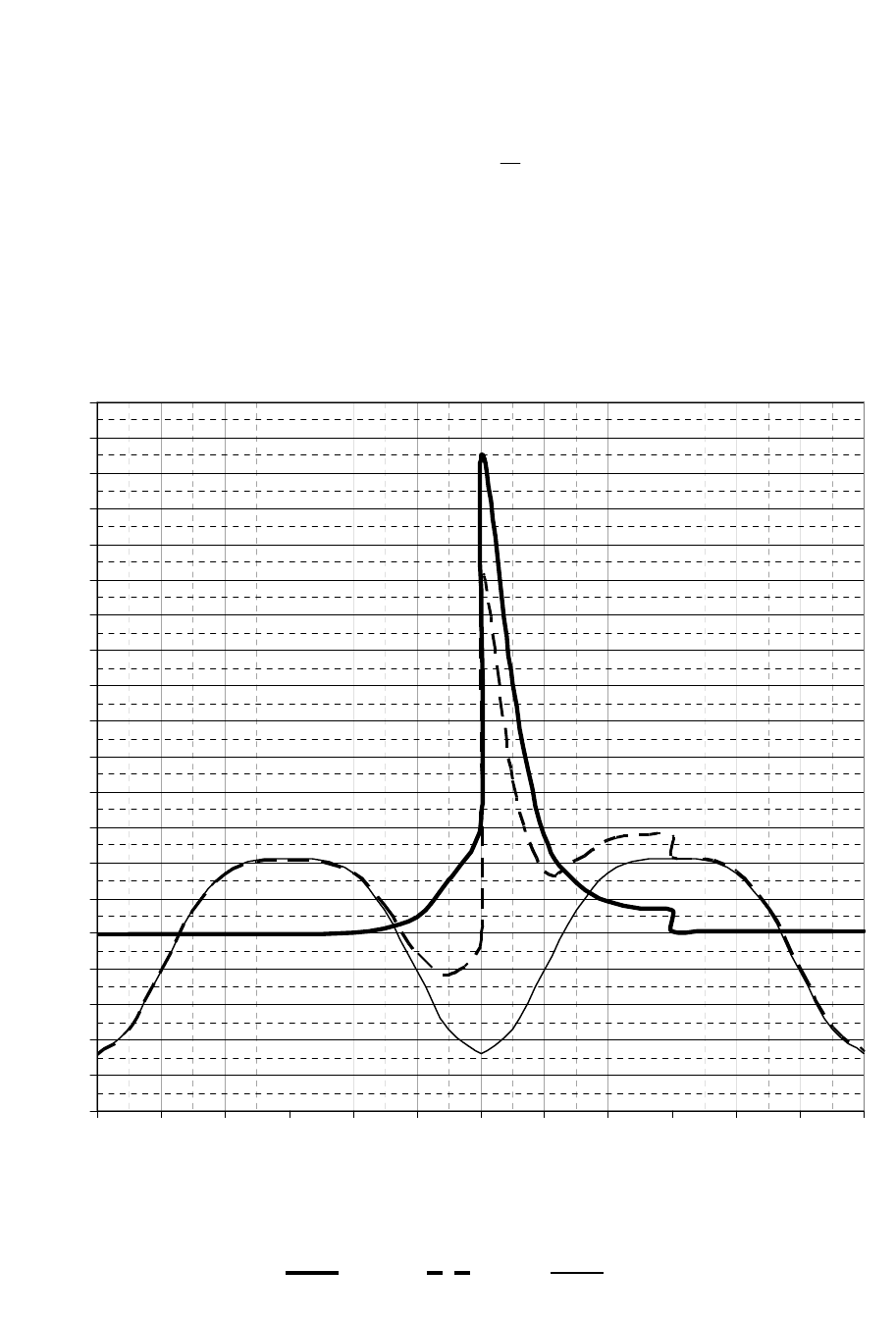
Графическая зависимость сил, действующих в кривошипно-шатунном
механизме, от угла поворота коленчатого вала показана на рис. 1.6.
Рис. 1.6. Диаграмма сил, действующих в кривошипно-шатунном
механизме
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
7
7,5
0 60 120 180 240 300 360 420 480 540 600 660 720
Угол поворота коленчатого вала, град
Давление, МПа
∆Рг; P; P

16
Контрольные вопросы
1. С какой целью определяют значение пути, скорости и ускорения
поршня?
2.
Методика построения индикаторной диаграммы в координатах P-V и
P-φ
.
3.
Как определяют силу инерции от поступательно движущихся масс?
4.
Как определяют суммарную силу от давления газов и инерциальных
сил?
5.
Методика определения сил, действующих в деталях КШМ.
2. РАСЧЕТ МАХОВИКА
2.1. Цель и задачи работы
Изучить методику расчета маховика, определить его массу и размеры
для конкретного двигателя.
2.2. Вводная часть
Основное назначение маховика – обеспечение равномерности хода
двигателя и создание необходимых условий для плавного движения маши-
ны с места.
Для автомобильных двигателей, работающих обычно с большой не-
догрузкой, характерен облегченный разгон машины и поэтому их махови-
ки имеют минимальные размеры.
В тракторных двигателях кинематическая энергия маховика должна
обеспечить плавное движение машины с
места и преодоление кратковре-
менных перегрузок. Поэтому маховики тракторных двигателей по сравне-
нию с автомобильными, имеют большую массу и размеры.
Расчет маховика сводится к определению момента инерции маховика
J
М
, основных его размеров, массы и максимальной окружной скорости.
2.3. Определение момента инерции маховика
Показателем, характеризующим изменение скорости вращения колен-
чатого вала за цикл, является коэффициент неравномерности хода
ср
ω
ω
ω
δ
minmax
−
=
, (2.1)
17
где ω
max
, ω
min
– максимальная и минимальная угловые скорости вра
щения коленчатого вала за цикл, рад/с;
30
n
ср
⋅
=
π
ω
– средняя угловая скорость за цикл, рад/с;
n – частота вращения коленчатого вала, мин
-1
.
Для автомобильных двигателей δ=0,01±0,02, для тракторных
δ=0,003±0,01.
Задаваясь значением δ, можно приближенно найти момент инерции
маховика. Для этого вначале определяют момент инерции всех движущих-
ся масс двигателя относительно оси вала по формуле
2
0
ср
изб
L
J
δω
=
, (2.2)
где L
изб
– наибольшая избыточная работа суммарного крутящего
момента, Н
·
м.
Для определения L
изб
многоцилиндрового двигателя строят график на-
бегающего крутящего момента М
кр
. Для этого необходимо знать изменение
удельной касательной силы Т (Н/м
2
) или RТFМ
nкр
=
(Н
·
м) в зависимости
от угла поворота коленчатого вала φ. Следует напомнить, что F
n
– площадь
поршня; R – радиус кривошипа.
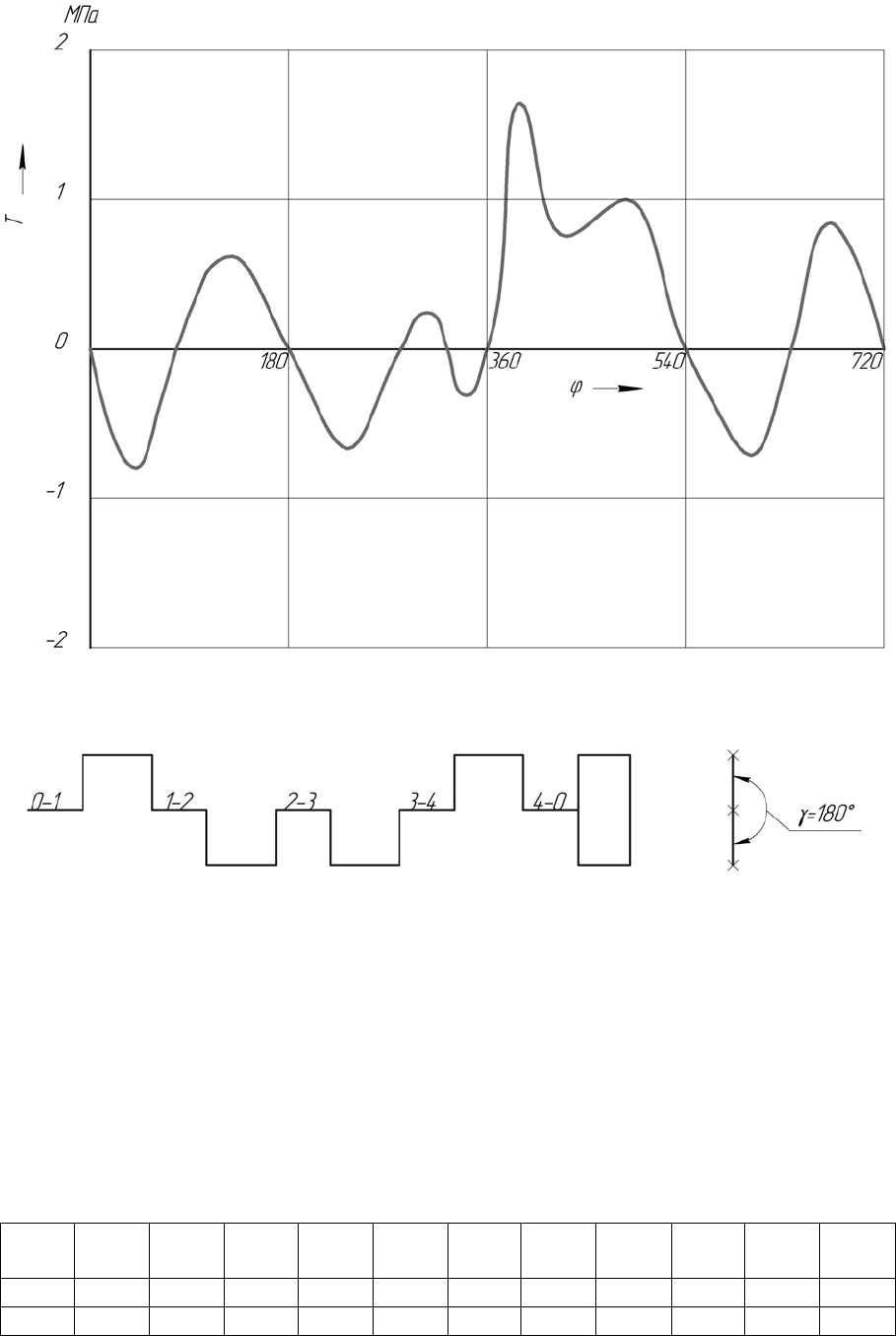
На рис. 2.1 показано изменение удельной силы Т в зависимости от φ.
На рис. 2.2 в качестве примера показана схема коленчатого вала 4-
цилиндрового двигателя с кривошипами под углом, равным 180
о
.
Крутящий момент передается последовательно от первого цилиндра к
четвертому (в нашем примере удельная сила Т), создавая запас энергии на
маховике. Накопленная энергия передается на привод механизмов транс-
миссии, гидравлических насосов и пр.
Для определения набегающего крутящего момента на конкретной ко-
ренной шейке и особенно на последней, необходимо знать начальные фазы
в каждом отдельном цилиндре. Положение поршня первого цилиндра бу-
дем считать в ВМТ, оно соответствует началу такта впуска. Начальную фа-
зу примем равной α = 0. Начальная фаза і-го цилиндра, определяющая, ка-
кой такт или какая часть такта, протекает в данном цилиндре, может быть
определена по схеме работы цилиндров или по
формуле:
γ
α
)1(
+
−
=
mi
i
, (2.3)
где i – число цилиндров;
m – номер вспышки по порядку;
γ – интервал между вспышками.
Для 4-тактного двигателя γ =720
о
/i, для 2-тактного двигателя γ =360
о
/i.
18
Например, для дизеля 4Ч13/14 (Д-440) α
1
= 0
о
; α
2
= 180
о
; α
3
= 540
о
; α
4
=
360
о
.
Для определения набегающего крутящего момента на промежуточные
коренные шейки и суммарного крутящего момента на шейку 4–0 состав-
ляют табл. 2.1, в которую в соответствии с начальными фазами для каждо-
го цилиндра вписывают значение удельной силы Т.
Таблица 2.1
Значение силы Т на различных коренных шейках
φ=α,
град
Т
1
,
МПа
Т
1-2
,
МПа
α
2
,
град
Т
2
,
МПа
Т
2-3
,
МПа
α
3
,
град
Т
3
,
МПа
Т
3-4
,
МПа
α
4
,
град
Т
4
,
МПа
Т
4-0
,
МПа
0 0 0 180 0 0 540 0 0 360 0 0
10 -0,3 -0,3 190 -0,1 -0,4 550 -0,1 -0,5 370 1 0,5
Рис. 2.2. Схема коленчатого вала
Рис. 2.1. График изменения удельной тангенциальной силы в зависимости от
ϕ
19
Складывая алгебраические значения Т, получим значение набегающе-
го момента на каждой коренной шейке. Эти данные необходимы для оцен-
ки наиболее нагруженной шейки. В табл. 2.1 в качестве примера показано
определение значения Т на каждой коренной шейке для двух значений φ.
Значение Т
4-0
представляет собой суммарное значение удельной силы Т,
действующей от всех кривошипов.
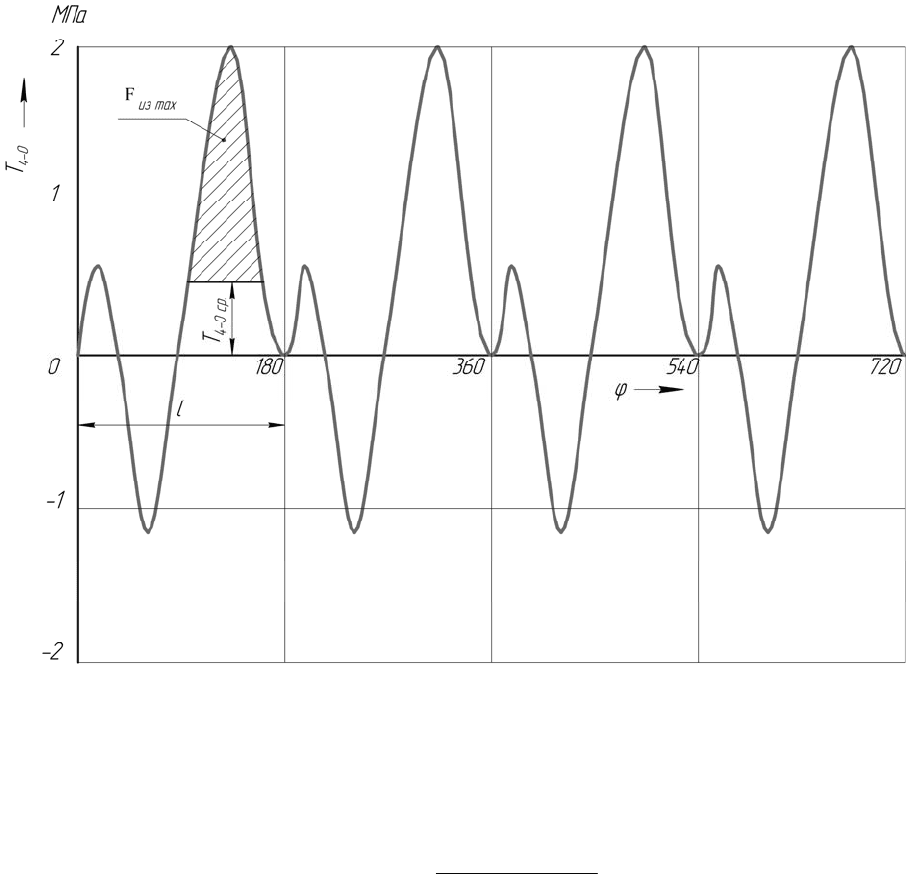
На рис. 2.3 показан график изменения Т
4-0
. Периодичность изменения
графика служит для контроля правильности выполнения расчетов.
Для определения среднего значения Т
4-0
определяют длину периода l, а
также площадь, заключенную между кривой и осью абсцисс:
l
FF
Т
∑∑
−+
−
−
=
04
. (2.4)
Далее определяют величину максимальной избыточной площади
F
изб.max
, м
2
, на участке l, м, выше линии Т
4-0 ср
. Затем определяют наиболь-
шую избыточную работу:
µ
⋅
=
maxизбизб
FL
, (2.5)
Рис. 2.3. График изменения силы T на коренной шейке 4-0
