Макаров В.А. (ред.) Задачи вступительных испытаний и олимпиад по физике в МГУ

Подождите немного. Документ загружается.

Биологический факультет

где

4πε

– приращение потенциальной энергии электрона при

его перемещении с поверхности шарика в бесконечно удаленную точку,

– модуль заряда электрона. Таким образом, в нашем случае уравнение

Эйнштейна приобретает вид:

eqhchc

4πε

где

λ – максимальная длина волны падающего света, при которой вы-

битые из шарика фотоэлектроны не будут возвращаться на него. Из по-

следнего равенства получаем ответ:

Reqhc

4// πε+λ

=λ

8. На рис. 77 изображены силы, действующие на материальную точ-

ку при максимальном отклонении математического маят-

ника от положения равновесия. Поскольку скорость мате-

риальной точки в этом положении равна нулю, то центро-

стремительное ускорение также равно нулю. Поэтому сила

натяжения нити

T равна по модулю проекции силы тяже-

сти на направление нити:

α= cos

mgT .

При прохождении маятником положения равновесия, когда

нить маятника занимает вертикальное положение, материальная точка

обладает скоростью и, следовательно, центростремительным ускорени-

ем. Из второго закона Ньютона, записанного для движения по окружно-

сти, в проекции на ось, направленную вертикально вверх, следует урав-

нение:

mgT

m −=

где

T – натяжение нити в этом положении, v – скорость материальной

точки,

– длина нити. При движении маятника от крайней точки к по-

ложению равновесия происходит превращение потенциальной энергии

Рис. 77

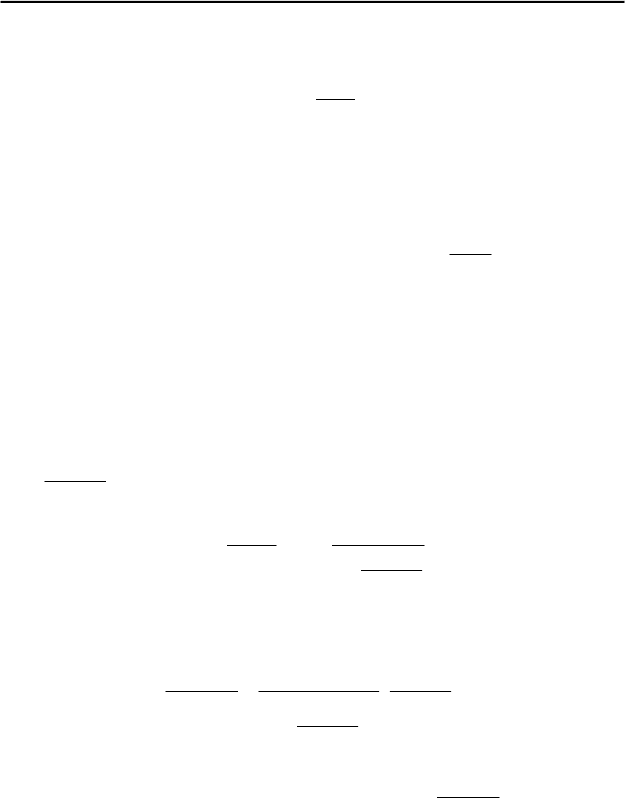
Решения задач

в кинетическую. Поэтому по закону сохранения механической энергии:

mgh

= ,

где

)cos1( α−= Lh – разница высот материальной точки в крайнем по-

ложении и в нижней точке. Решая записанные выражения, находим:

)cos1(2

α−+= mgmgT .

Учитывая, что

kTT = , получаем ответ:

⎟

⎠

⎞

⎜

⎝

⎛

=α

arccos

9. В электрической цепи, представленной в условии задачи, при ра-

зомкнутом ключе K ток течет только через резистор

R (конденсатор

представляет собой разрыв электрической цепи, и ток через резистор

R равен нулю). При замкнутом ключе внешняя цепь состоит из парал-

лельно соединенных резисторов

R ,

R и имеет сопротивление

. Полный ток во внешней цепи в обоих случаях:

Приравнивая мощности, выделяющиеся во внешней цепи при разомк-

нутом и замкнутом ключе K, имеем:

)(

⋅

⎟

⎠

⎞

⎜

⎝

⎛

Из решения этого уравнения получаем ответ:

3,1

−

R Ом.

Биологический факультет

10. Работа, совершенная газом за цикл численно равна площади

трапеции 1234 на pV–диаграмме:

)()(

123241

VVppppA −−+−= .

Согласно уравнению Клапейрона-Менделеева для одного моля идеаль-

ного газа имеем:

111

RTVp = .

Для изобарного процесса

43 − по закону Гей-Люссака:

VV =

;

для изохорного процесса

14 − по закону Шарля:

pp =

;

для состояний 1 и 2 по закону Бойля-Мариотта:

1122

VpVp = .

Решая записанную систему уравнений, получаем ответ:

6251

≈

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

+−=

TRT

A Дж.

Решения задач

ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ

И КИБЕРНЕТИКИ

I. МЕХАНИКА

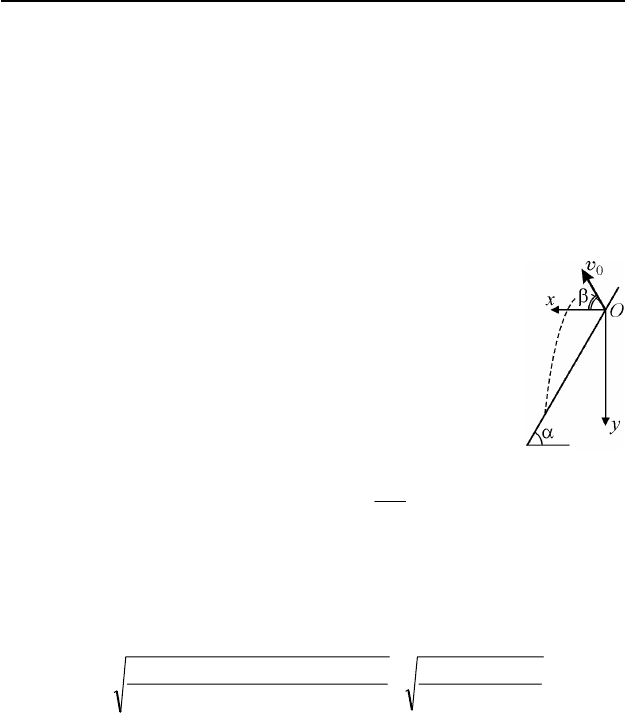
I.1. При упругом ударе о наклонную плоскость составляющая ско-

рости шарика, параллельная плоскости, не изменяется, а

составляющая, перпендикулярная плоскости, оставаясь

той же по величине, меняет направление на противопо-

ложное. Следовательно, после удара шарик отскочит от

наклонной плоскости со скоростью

v под углом

α−π=

2 к горизонту. Кинематические уравнения дви-

жения шарика в системе координат, изображенной на рис.

78, имеют вид:

tx ⋅

= cos

v ,

sin

ty +⋅β−= v

В точке падения шарика на плоскость выполняются соотношения:

lx = , α= tgly .

Исключая из записанных выражений время, получаем ответ:

|2cos|sin2

cos

)]2tg()[tg2(cos2

αα

α−π+αα−π

glgl

v .

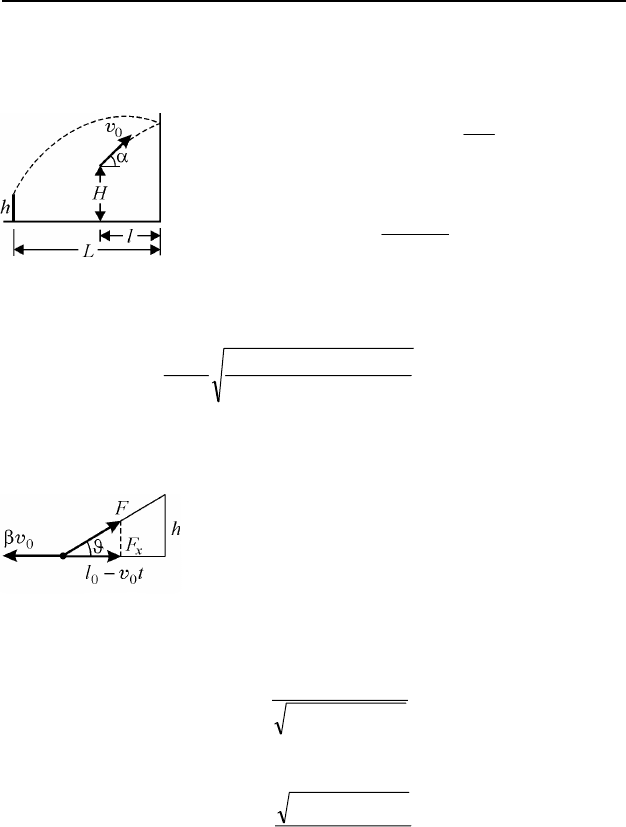
I.2. Траектория мяча, соответствующая максимальной скорости,

удовлетворяющей условию задачи, изображена на рис. 79. При упругом

ударе о стенку вертикальная составляющая скорости мяча не изменяет-

ся, а горизонтальная, оставаясь той же по величине, меняет направление

Рис. 78

Факультет ВМиК

на противоположное. Зависимость высоты мяча над поверхностью зем-

ли имеет вид:

sin

tHy −⋅α+=

v .

Время полета мяча до ограждения

cos

Мяч не перелетит через ограждение, если

hty ≤)(

Исключая из записанных выражений время, получаем ответ:

17,7

]tg)()[(2cos

≈

α++−α

lLhH

glL

м/с.

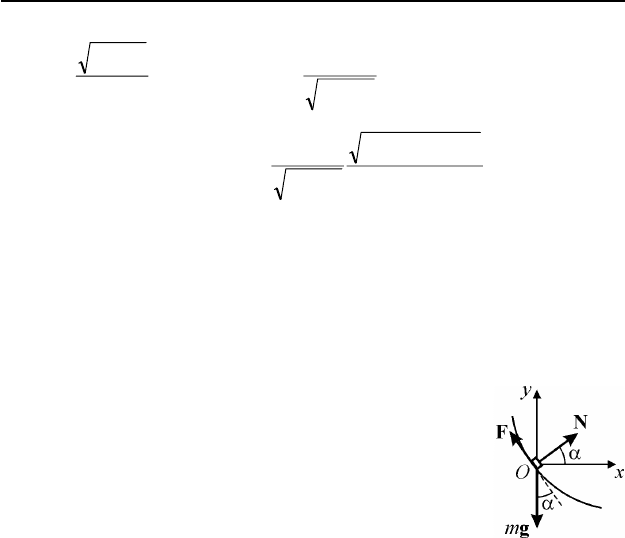
I.3. Лодка движется равномерно под действием двух сил: горизон-

тальной составляющей силы натяжения веревки

и силы сопротивления воды. Модули этих сил на

рис. 80 обозначены через

F и

, где

– ко-

эффициент сопротивления воды. По второму

закону Ньютона имеем:

F . Из рисунка

видно, что

ϑ= cosFF

, где ϑ – угол, который

веревка образует с горизонталью, причем

)(

cos

htl

+−

−

=ϑ

Объединяя записанные равенства, получаем:

htl

)(

−

+−

β=

Положив в последнем равенстве

0=t ,

)0( FF = , имеем:

Рис. 79

Рис. 80

Решения задач

β= v

, откуда

=βv

Ответ:

htl

FtF

)(

−

+−

Замечание: Из этой формулы видно, что по мере приближения лод-

ки к пристани сила

неограниченно возрастает. Приведенный ответ

имеет смысл до тех пор, пока

не превысит силу тяжести, действую-

щую на лодку.

I.4. Брусок движется по горизонтальной окружности под действием

сил, изображенных на рис. 81, где

gm – сила тяжести,

N – нормальная составляющая силы реакции сферы,

F – сила трения. В проекциях на оси OX и OY непод-

вижной координатной системы имеем:

α−α=αω sincoscos

FNRm ,

0sincos =−α+α mgNF .

Исключая отсюда

N , находим

)sin(cos

αω−α= RgmF .

Если угловая скорость вращения сферы такова, что

gR >αω sin

, то

сила трения направлена противоположно. В общем случае ответ имеет

вид:

|sin|cos

αω−α= RgmF .

I.5. На правую чашу весов, заполненную водой до краев, действует

сила

NMgF += ,

Рис. 81

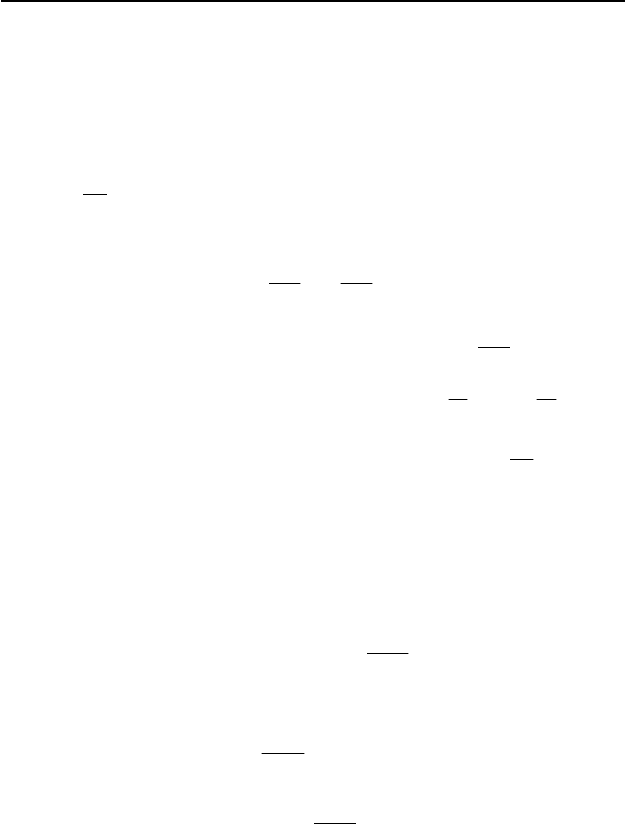
Факультет ВМиК

где ShM

= – масса воды в этой чаше, N – сила давления падающих

капель дождя. Поскольку соударение капель с водой, находящейся в

чаше, является неупругим, по второму закону Ньютона имеем:

tgmNm ∆⋅∆−=⋅∆ )(v ,

где

m ∆

=∆ – масса дождевых капель, попадающих в чашу за малое

время

t∆ . Отсюда

tN ∆

+∆

=∆

Учитывая малость

t∆ , находим, что приближенно

≈

N . Весы будут

уравновешены, если масса гири на левой чаше

m +ρ==

. Объе-

диняя записанные выражения, получаем ответ:

5,501 =

⎟

⎠

⎞

⎜

⎝

⎛

+ρ=

Shm

г.

I.6. В момент, когда достигается максимальное сжатие пружины,

скорость бруска обращается в нуль. По закону изменения механической

энергии имеем:

тр

sin)( A

llmgmgH +

∆

+α∆−=

где

тр

– модуль работы силы трения

тр

на перемещении бруска S ,

причем

= cos

тр

mgF

⎟

⎠

⎞

⎜

⎝

⎛

∆−−

= )(

sin

S . Следовательно,

⎟

⎠

⎞

⎜

⎝

⎛

∆−−

αµ= )(

sin

cos

тр

mgA .

Решения задач

Объединяя записанные выражения, получаем квадратное уравнение

относительно

l∆ :

sin

)cos(sin

⎟

⎠

⎞

⎜

⎝

⎛

−

αµ−α−∆αµ−α−∆ l

Поскольку по условию задачи предоставленный самому себе брусок

приходит в движение,

>α cossin . Кроме того, l

sin

. Поэтому

свободный член в квадратном уравнении заведомо отрицателен, и, сле-

довательно, корни этого уравнения существуют. Условию задачи удов-

летворяет положительный корень. Ответ:

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

αµ−α

α−

⋅

++αµ−α=∆

)cos(sin

)sin(

sin

11)cos(sin

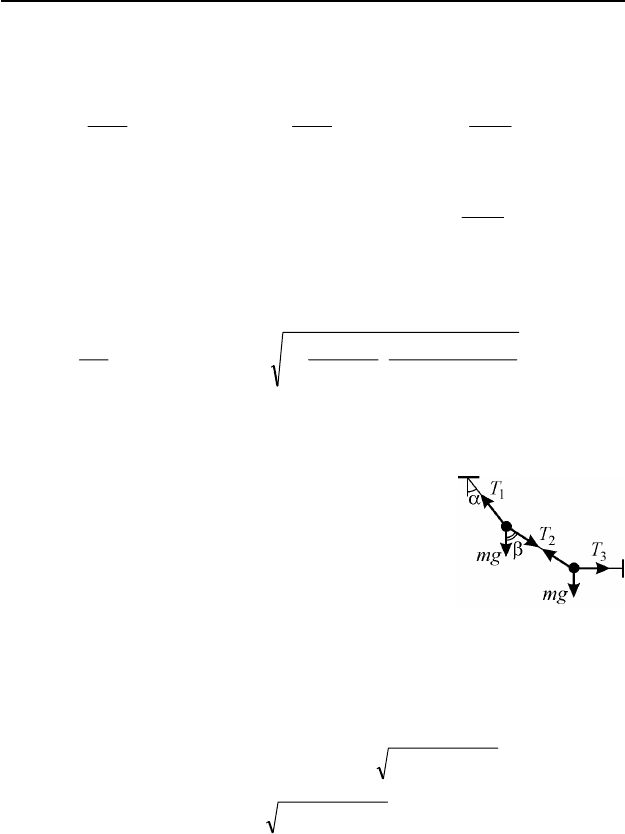
I.7. Шарики находятся в равновесии под действием сил, модули и

направления которых изображены на рис. 82, где

mg – модуль силы тяжести. В проекции на гори-

зонтальное и вертикальное направления условия

равновесия шариков имеют вид:

=α sinsin

TT ,

+=α coscos

TmgT ,

sin TT =

, mgT =

cos

Отсюда вытекают следующие равенства:

=α cos2cos

TT , )sin34()cos4(sin

222

β−=β+β= TTT .

Из последнего равенства находим

3/)4(sin

TTT −=β . Ответ:

3/)4(

TTT −= .

Рис. 82

Факультет ВМиК

I.9. Стакан будет находиться под водой в безразличном равновесии

при выполнении условия

Vgmg

= ,

где

V – объем воздуха в стакане. Отсюда

. По закону Бойля-

Мариотта

pVVp =

где

ghpp

– давление воды на глубине h . Объединяя записанные

выражения, находим

)(

h −ρ

При меньшей глубине погружения предоставленный самому себе ста-

кан будет всплывать. Наоборот, при увеличении глубины погружения

стакан начнет опускаться вниз, так как с ростом давления воды вытал-

кивающая сила будет уменьшаться. Ответ:

10)(

=−ρ

≥ mV

h м.

*I.9. Пусть p – давление, создаваемое насосом, v – скорость воды

в шланге. Согласно уравнению Бернулли,

vρ

+ρ= ghp

Работа

VpA ∆=∆

, совершаемая насосом по перемещению воды объе-

мом

tSV ∆=∆ v , равна

tSghA ∆

⎟

⎠

⎞

⎜

⎝

⎛

+ρ=∆ v

По условию

τ= vSV , откуда

v . Объединяя записанные выраже-

Решения задач

ния и учитывая, что

∆

, получаем ответ:

⎟

⎠

⎞

⎜

⎝

⎛

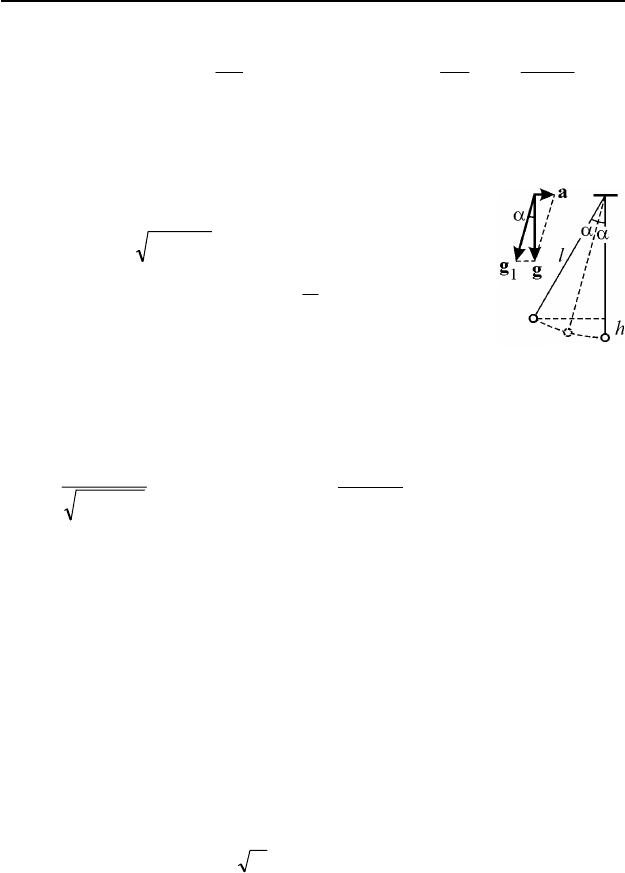
I.10.

По закону сложения ускорений ускорение свободного падения

относительно системы отсчета, связанной с вагоном,

agg −=

. Из рис. 83 видно, что модуль этого ускоре-

ния равен

gag += , а само ускорение образует с

вертикалью угол

α , причем

=α

tg . Следовательно, в

момент начала движения вагона маятник оказывается

отклоненным от устойчивого положения равновесия на

угол

α . В результате возникших колебаний макси-

мальный угол отклонения маятника от вертикали составит

α2 . Как

видно из рисунка,

α=α−=

sin2)2cos1( llh

. Используя формулу

α+

=α

tg1

sin

, получаем ответ:

II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

II.1.

Поскольку сжатие пружины совпадает с высотой поршня над

дном сосуда, давление газа пропорционально его объему:

Vp ~ . Пусть

p ,

V и

T – начальные давление, объем и температура газа. Уравне-

ния начального и конечного состояний газа имеют вид:

000

RTVp

000

RmTnVnp

Отсюда

mn =

. Ответ: 41,1≈= mn .

Рис. 83