Макаров В.А. (ред.) Задачи вступительных испытаний и олимпиад по физике в МГУ

Подождите немного. Документ загружается.

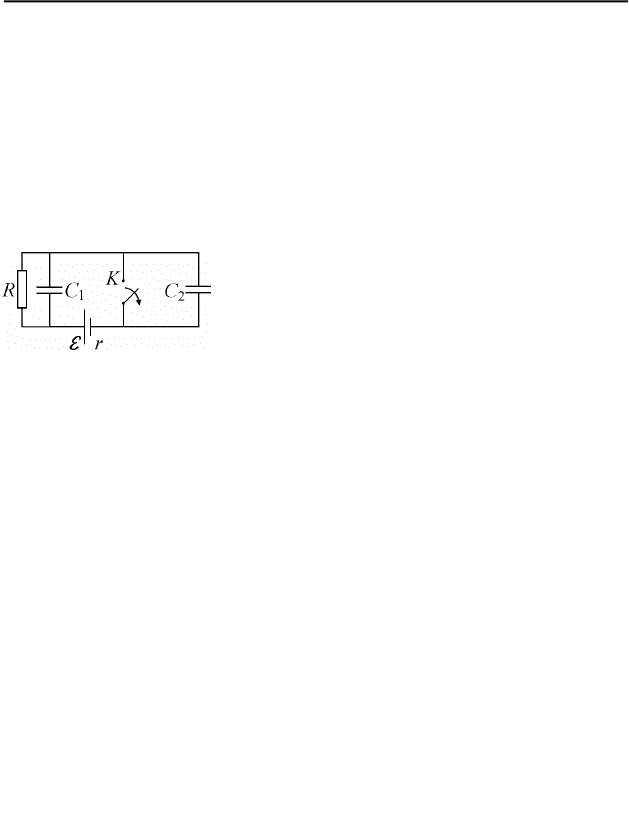
Олимпиада «Ломоносов – 2007»

=Q мкКл и 3

=Q мкКл. Незаряженный металлический шарик на

тонкой длинной диэлектрической палочке подносят к первой сфере и

касаются ее. Затем этот шарик переносят ко второй сфере и касаются ее

таким же образом. Найти заряд

к2

Q оставшийся на второй сфере, если

заряд шарика после его удаления от второй сферы оказался равным

5,0

мкКл.

III.3. В цепи, схема которой изображена на рис. 56, ключ

К в тече-

ние длительного времени находился в замк-

нутом состоянии. В некоторый момент ключ

разомкнули. Какое количество теплоты

выделится в схеме после этого? Емкости кон-

денсаторов:

=C мкФ, 2

=C мкФ, сопро-

тивление резистора

4=R

Ом, ЭДС источни-

ка

10=E В, его внутреннее сопротивление 1=r Ом.

III.4. Конденсатор ёмкостью

1=C мкФ полностью зарядили от ис-

точника с ЭДС

10=E В и отключили от него. Затем конденсатор замк-

нули на катушку, индуктивность которой равна

30=L

мГн. Найти силу

тока

в LC–контуре в тот момент, когда заряд конденсатора умень-

шится в

2=n раза по сравнению с максимальным. Потерями в LC–

контуре пренебречь.

III.5. Из тонкого провода сопротивлением 10=R Ом изготовили

квадратную рамку со стороной 10=a см. Рамку поместили в однород-

ное магнитное поле, вектор индукции которого перпендикулярен плос-

кости рамки и по модулю равен 1,0=B Тл. К вершинам двух соседних

углов рамки подключили источник с малым внутренним сопротивлени-

ем и ЭДС 3=E В. Найти силу, действующую на рамку со стороны

магнитного поля.

Рис. 56

Условия задач

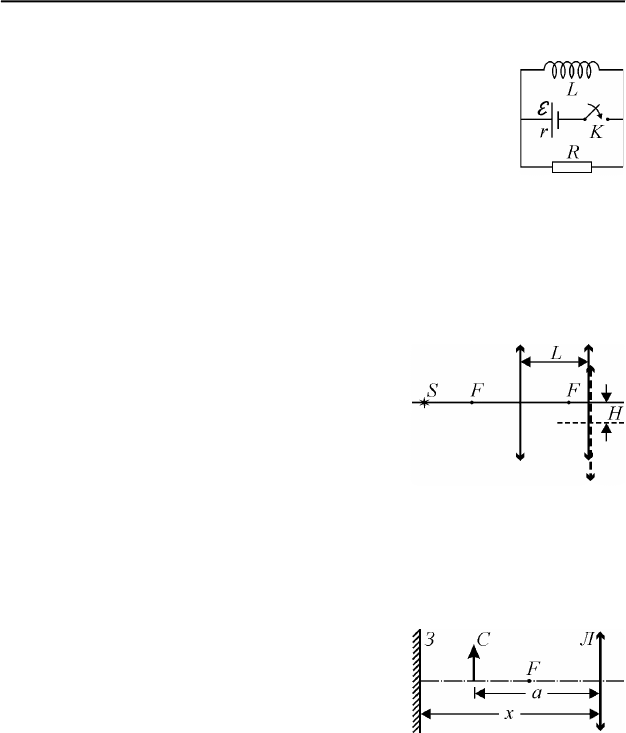
III.6. В цепи, схема которой показана на рис. 57, в не-

который момент замыкают ключ

K. Найти напряжение U

на катушке к тому моменту, когда через резистор проте-

чет заряд

q . Индуктивность катушки

, сопротивление

резистора

, ЭДС источника E , а его внутреннее сопро-

тивление

IV. ОПТИКА

IV.1. Оптическая система состоит из двух одинаковых тонких соби-

рающих линз с фокусным расстоянием

каждая. Линзы расположены на расстоянии

друг от друга (

2<<

) так, что их

главные оптические оси совпадают (см.

рис. 58). Слева от системы на расстоянии

от левой линзы находится точечный источник

света

S . На какое расстояние h сместится

изображение источника, даваемое этой сис-

темой, если правую линзу сдвинуть перпендикулярно ее оптической оси

на расстояние

IV.2. Оптическая система состоит из собирающей линзы

Л с фокус-

ным расстоянием

и плоского зеркала З,

плоскость которого перпендикулярна главной

оптической оси линзы. Между линзой и зер-

калом находится стержень

C, расположенный

перпендикулярно главной оптической оси

линзы. Расстояние от стержня до линзы равно

a , причем Fa > . Найти такое расстояние

между линзой и зеркалом, при котором отношение размеров двух дей-

ствительных изображений стержня равно

k ( 1>k ).

Рис. 57

Рис. 58

Рис. 59

Олимпиада «Ломоносов – 2007»

IV.3. На катод фотоэлемента падает свет с мощностью 3,0=N Вт.

Длина волны света 330=

нм. Найти силу тока насыщения

, если на

каждые 10=k падающих на катод световых квантов приходится один фо-

тоэлектрон. Считать, что постоянная Планка

106,6

−

⋅=h Дж⋅с, скорость

света в вакууме

103⋅=c м/с, модуль заряда электрона

106,1

−

⋅=e Кл.

IV.4. Два когерентных световых пучка проходят в воздухе одинако-

вые расстояния от источников до некоторой точки A. На пути первого

пучка перпендикулярно ему помещают прозрачную пленку толщиной

5,2=d мкм с показателем преломления 3,1=n . На сколько в результа-

те этого изменится сдвиг фаз между световыми волнами в точке A, если

длина волны света в вакууме 5,0=λ мкм? Показатель преломления воз-

духа 0,1

=n .

Решения задач

РЕШЕНИЯ ЗАДАЧ

ФАКУЛЬТЕТ НАУК О МАТЕРИАЛАХ

1. Пусть

t – время, затраченное мотоциклистом на движение от на-

чала колонны к ее концу, а

t – время, затраченное на движение в об-

ратном направлении. Пути, пройденные мотоциклистом при этих дви-

жениях, соответственно равны

tls v−= и

tls v+= . Учитывая, что в

обоих случаях мотоциклист начинает движение из состояния покоя,

имеем:

s =

, или

v−=

v+=

. Отсюда

++−=

++=

Полный путь, пройденный мотоциклистом,

)(2

1221

ttlsss −+=+= v .

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

км.

2. Мысленно выделим на поверхности планеты небольшую площад-

ку площадью

S∆ . Так как основная часть атмосферы сосредоточена

вблизи поверхности планеты (по условию атмосфера тонкая), то атмо-

сферное давление равно

∆

, где m∆ – масса столба атмосфер-

ного газа, находящегося над выделенной площадкой,

– ускорение

свободного падения на поверхности планеты. Следовательно, полная

масса атмосферы m пропорциональна площади

S поверхности плане-

ты, то есть

4π

== .

Факультет наук о материалах

Учитывая, что

g =

, где ρπ=

– масса планеты, получаем

ответ:

3. Максимальное значение скорости груза, совершающего верти-

кальные колебания на пружине, достигается при прохождении грузом

положения равновесия, в котором сумма силы тяжести и силы упруго-

сти растянутой пружины, действующих на груз, обращается в нуль.

Примем положение равновесия груза за нулевой уровень отсчета потен-

циальной энергии системы. При свободных незатухающих колебаниях

полная

механическая энергия системы сохраняется, откуда следует ра-

венство:

222

vv mmxk

Выражая из этого равенства жесткость пружины, находим ответ:

04,0

−

Н/м.

4. В соответствии с уравнением Менделеева–Клапейрона давление

азота в начальном состоянии равно

mRT

, где V – объем сосуда,

m – масса азота,

– его молярная масса. Давление газа в конечном

состоянии определяется по закону Дальтона:

21к

ppp += , где

mRT

)2/(

= и

mRT

)1( α−

– парциальные давления атомарного и молекулярного азота,

– иско-

мая доля диссоциировавших молекул. Следовательно,

mRT

)1(

α+

Решения задач

По условию

нк

npp = . Объединяя записанные выражения, находим

−=α

Отметим, что относительная доля диссоциировавших молекул не может

превышать единицу. Полагая в последнем равенстве

1<α , получаем,

что ответ имеет смысл при

/2 TTn < . Следовательно, в общем виде

ответ формулируется так:

−=α

при

n <

; иначе решения нет.

5. Предложенное в условии задачи устройство предназначено для

преобразования количества теплоты

Q , полученного маслом при нагре-

вании, в механическую работу

по перемещению рамы. В соответст-

вии с определением коэффициента полезного действия, имеем

=η .

Количество теплоты, получаемое маслом,

()

CttQ

−= , совершаемая

при этом работа

hFA = . Ответ:

)(

ttC

−

=η

6. На рис. 60 приведена эквивалентная схема рассматриваемой цепи,

где сопротивления

LlRR /

= , LlLRR /)(

−= . Так

как резисторы

R и

R соединены параллельно, то

111

RRR

Отсюда находим, что искомое сопротивление

R , которое покажет ом-

метр, равно

)(

RlLl

−

7. Сопротивление цепи, состоящей из последовательно соединен-

ных резистора, катушки и конденсатора, и подключенной к источнику

гармонического напряжения с циклической частотой

, равно

Рис. 60

Факультет наук о материалах

⎟

⎠

⎞

⎜

⎝

⎛

−ω+=

LRZ

где

R – сопротивление резистора. Мощность, потребляемая цепью от

источника,

ϕ= cos

где

U – амплитуда напряжения источника,

– сдвиг по фазе между

током в цепи и напряжением источника. Поскольку

=ϕcos , выраже-

ние для мощности, потребляемой цепью, можно переписать в виде

= .

Так как при замыкании конденсатора потребляемая цепью мощность не

изменяется, то величина Z остается неизменной:

)(

LR ω+=

⎟

⎠

⎞

⎜

⎝

⎛

−ω+

Отсюда получаем ответ:

LC2

=ω

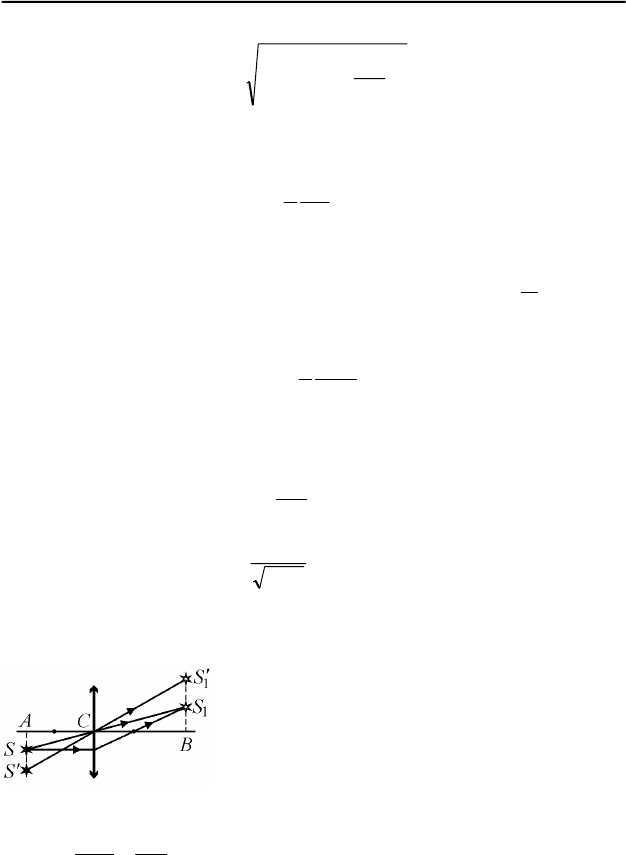
8. Пусть в момент времени

источник находится в точке S , а его

изображение – в точке

S (см. рис. 61). За

время

t∆ источник и изображение перемес-

тятся и в момент

tt ∆+ займут положения S

′

, соответственно, причем tVSS ∆=

′

, а

tSS ∆=

′

. Так как ASC∆ подобен BCS

∆ ,

SCS

′

∆

подобен CSS

′

∆

, справедливо ра-

венство

′

. В соответствии с формулой линзы

Рис. 61

Решения задач

FBCAC

111

где

bBC = . Отсюда следует, что

−

Объединяя записанные выражения, получаем ответ:

−

ФАКУЛЬТЕТЫ ХИМИЧЕСКИЙ,

БИОИНЖЕНЕРИИ И БИОИНФОРМАТИКИ

ВАРИАНТ 1

1.3. В инерциальной системе отсчёта частица движется по прямой, если

сумма действующих на неё сил равна нулю. Следовательно, силы,

действующие на протон со стороны электрического и магнитного поля,

направлены в разные стороны и равны по величине. Из уравнения

движения протона (второго закона Ньютона)

0=− BqqE v

находим искомую скорость:

102 ⋅==

v м/с.

1.4. Все необходимые построения выполнены на

рис. 62. Прежде всего, для построения хода искомо-

го луча надо найти положения фокусов линз – по

условию они совпадают для рассеивающей и соби-

рающей линз. Проведём побочную оптическую ось

АВ, параллельную падающему лучу 1. Продолжение

луча 2 пересекается с этой осью в передней фокаль-

ной плоскости линз. Отложив такое же расстояние за плоскостью линз,

Рис. 62

Факультеты химический, биоинженерии и биоинформатики

находим заднюю фокальную плоскость. Луч 3 пересекается с побочной

оптической осью в точке пересечения её с этой фокальной плоскостью.

1.5. Из уравнения состояния идеального газа

nkTp = следует, что

давление газа

p пропорционально произведению его абсолютной тем-

пературы

T и концентрации молекул

. Здесь

–

постоянная Больц-

мана. По условию температура газа увеличилась в 2 раза. Когда полови-

на двухатомных молекул распалась на атомы, частиц в сосуде стало в

1,5 раза больше. Поскольку объем сосуда не изменился, концентрация

частиц также возросла в 1,5 раза. Ответ: давление газа увеличилось в

3=α раза.

1.6. Поскольку по условию сопротивлением воздуха можно пренебречь,

при решении проще всего воспользоваться законом сохранения механи-

ческой энергии системы «сосулька + Земля». За нулевой уровень отсче-

та потенциальной энергии тяготения удобно выбрать горизонталь, про-

ходящую через точку соударения с поверхностью крыши

BC. Точка от-

рыва

B находится выше этого уровня на α= sinlh , поэтому равенство

механических энергий в моменты времени, когда сосулька находится в

точке

B и в точке касания с участком крыши BC можно записать так:

sin

vv mn

mgl

=α+

Отсюда нетрудно получить ответ:

sin2

−

1.7. Выберем инерциальную систему отсчёта, связанную с Землей,

направив координатную ось

Oy вертикально вверх к точке подвеса нити.

На шарик действуют три силы – сила тяжести

gm , сила натяжения нити

T и сила Лоренца

F (см. рис. 63). Запишем уравнение движения ша-

рика при прохождении им нижней точки траектории в проекции на ось

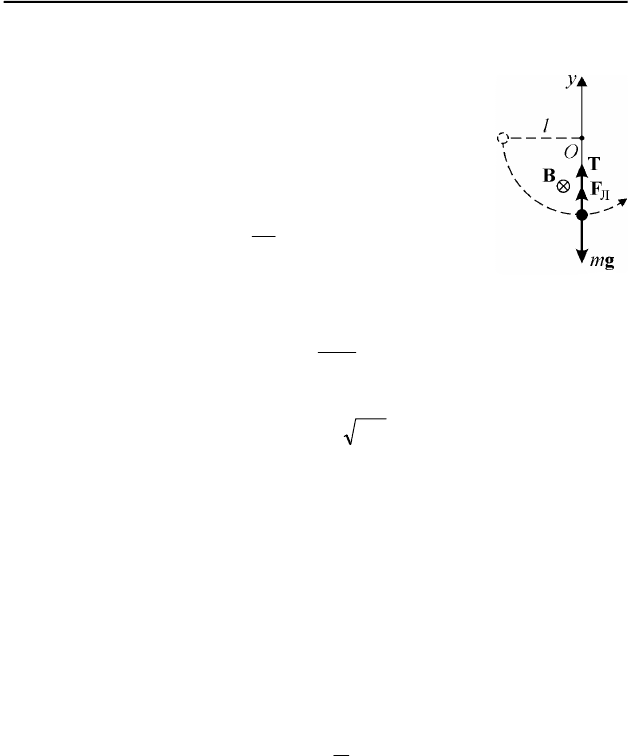
Решения задач

mgFTma −+=

Лц.с.

Здесь учтено, что по правилу левой руки сила Лоренца

F , действующая на положительно заряженный ша-

рик, направлена перпендикулярно скорости и вектору

магнитной индукции поля

B вдоль нити вверх. Цен-

тростремительное ускорение шарика равно:

ц.с.

= .

Скорость шарика в нижней точке траектории легко

найти из закона сохранения механической энергии:

mgl =

Решая совместно записанную систему уравнений, получаем ответ:

glqBmgT 23 −= .

1.8. При нормальном падении на дифракционную решетку плоскопа-

раллельного пучка монохроматического света от лазера дифракционные

максимумы располагаются симметрично относительно центрального (ну-

левого) максимума. Угловое положение максимумов определяется ус-

ловием:

λ=

md sin ,

где

m – порядок дифракции. Поскольку угол дифракции не может пре-

вышать 90

° ( 1sin ≤

), то максимальный порядок доступного для на-

блюдения дифракционного максимума равен

⎥

⎦

⎤

⎢

⎣

⎡

max

где символ

][L означает целую часть числа. По условию наблюдаются

всего

7=k максимумов. Это означает, что в данном случае 3

max

=m .

Следовательно, период решетки

λ>

max

md . Однако, период решетки

Рис. 63