Макаров В.А. (ред.) Задачи вступительных испытаний и олимпиад по физике в МГУ

Подождите немного. Документ загружается.

Физический факультет

120

FCACB

111

=−

Величина

CA/1 входит в записанное выражение со знаком «минус»,

потому что изображение является мнимым. Поскольку

CSB∆ подобен

ACS

∆

, то

aCB

∆+

, откуда

−

∆

aCBCA

−

∆

=∆+=

Подставляя эти выражения для

CB и CA в записанную выше формулу

линзы, получаем ответ:

)(

hhF

−

=∆

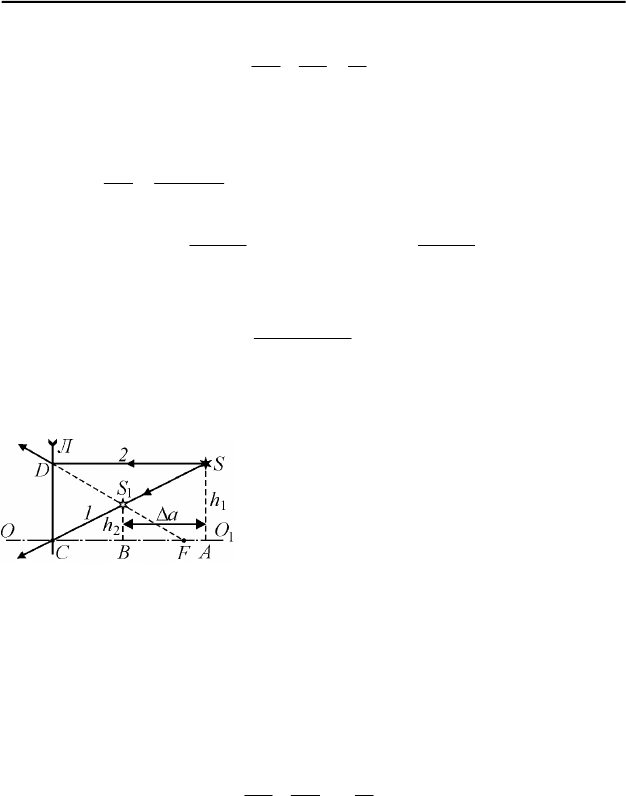
IV.3. Источник S и его изображение

должны лежать на одной

прямой – луче

1, проходящем через опти-

ческий центр С линзы (см. рис. 99). Поэто-

му, проведя прямую

до ее пересечения

с оптической осью

OO в точке С, можно

установить местонахождение линзы

Л. Луч

2, выходящий из источника параллельно

главной оптической оси, преломляется в

точке

D линзы Л, и после этого сам луч (или его продолжение) должен

пересечь эту ось в главном фокусе

. Местонахождение главного фо-

куса можно установить, проведя от точки

D через точку

прямую

до ее пересечения с оптической осью

OO в точке F. Таким обра-

зом, изображение источника является мнимым, а линза – рассеивающей.

В соответствии с формулой тонкой линзы имеем:

FCBCA

111

−=− .

Рис. 99

Решения задач

121

Величины CB/1 и F/1 входят в записанное выражение со знаком «ми-

нус» потому, что изображение является мнимым, а линза – рассеиваю-

щей. Поскольку

BCS

∆ подобен

CSA∆

, то

aCB

∆+

, откуда

−

∆

aCBCA

−

∆

=∆+=

Подставляя эти выражения для

CA и CB в записанную выше формулу

линзы, получаем ответ:

)( hh

ahh

−

∆

−=

ОЛИМПИАДА «ЛОМОНОСОВ – 2007»

I. МЕХАНИКА

I.1. Обозначим расстояние CO

через

(см. рис. 100). Тогда иско-

мая скорость равна

=v , где точка над буквой

означает производную от

по времени. Из

COO∆ по теореме синусов можно записать:

γ sinsin

. Учитывая, что

−α−π=

, из

этой формулы находим

β+α

sin

)sin(

hx .

При дифференцировании данного выражения по времени примем во

внимание, что производная от частного двух функций, зависящих от

времени (например

)(ty и

)(tz

), вычисляется по формуле:

zyzy

−

⎟

⎠

⎞

⎜

⎝

⎛

Рис. 100

Олимпиада «Ломоносов – 2007»

122

а производная от сложной функции ))(( tzy равна

zzyzy

)()( =

; например,

α⋅α=α

cossin

С учетом сказанного получаем:

α⋅αβ+α−β+α⋅αβ+α

sin

cos)sin()(sin)cos(

В нашем случае Lu /

−=β

, Lu /

−=

и Luu /)()(

+=γ+β−=α

. Знак

«минус» в первых двух выражениях отражает тот факт, что при указан-

ных в условии направлениях скоростей

u и

u углы

уменьша-

ются. Объединяя записанные выражения, находим ответ:

+α+−α

+α

212

sin

cos)sin()(sin)cos(

uuu

v .

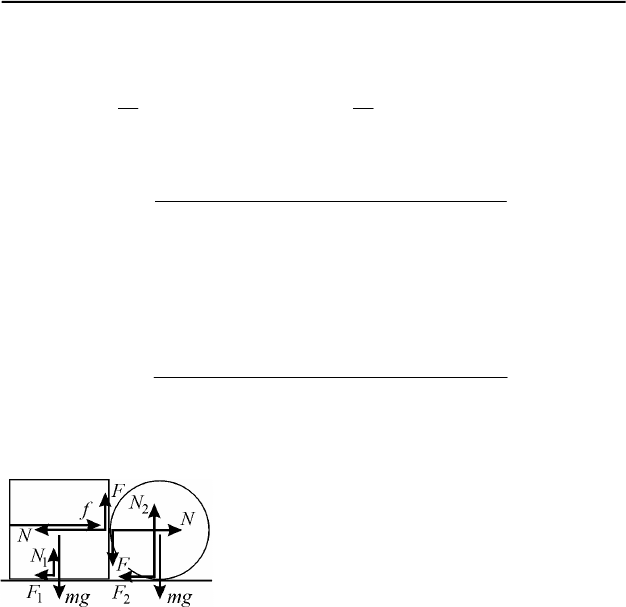
I.2. Куб и цилиндр движутся под действием сил, модули и направ-

ления которых изображены на рис. 101, где

mg – модуль силы тяжести, N – модуль

нормальной составляющей силы взаимодей-

ствия куба и цилиндра,

– модуль силы

трения между кубом и цилиндром,

N и

– модули нормальных составляющих сил

взаимодействия куба и цилиндра со столом,

F и

F – модули сил трения, возникающих

при скольжения куба и цилиндра по столу. По второму закону Ньютона

уравнения движения центров масс куба и цилиндра в проекции на гори-

зонтальное направление запишутся как:

FNfma −−= ,

FNma −= ,

где a – модуль ускорения этих тел. В проекции на вертикальное на-

правление имеем:

mgNF −+=

0 , mgFN −−=

0 .

Отсюда

FmgN −=

, FmgN +=

. Поэтому силы трения скольжения

Рис. 101

Решения задач

123

)(

FmgNF −

= , )(

FmgNF +

= .

Поскольку цилиндр по условию движется, не вращаясь, сумма момен-

тов сил

F относительно его оси равна нулю, откуда следует, что

FF = . При этом сила трения покоя

достигает максимального зна-

чения:

= . Следовательно,

NN = . Объединяя эти соотношения с

записанными выше выражениями для сил

F и

F , получаем, что

µ−

µ−µ

)21(

µ−

Подставляя найденные значения сил в уравнения движения центров

масс куба и цилиндра, находим ответ:

)1(2 µ+

I.3. При решении этой задачи придётся использовать как законы со-

хранения, так и законы кинематики. Прежде всего, выясним, какие вели-

чины сохраняются в системе «шарик + клин». Удар абсолютно упругий,

поэтому механическая энергия системы до и после удара одинакова.

Можно приравнять кинетическую энергию шарика непосредственно

перед соударением и кинетическую энергию клина и шарика сразу по-

сле

соударения:

222

Mumm

Здесь

v и v – скорости шарика до и после удара,

– скорость клина

после удара.

Импульс системы «шарик + клин» в результате соударения изменяется:

до удара он горизонтален, а после удара появляется вертикальная со-

ставляющая этого импульса, связанная с отскочившим вверх шариком.

Это обусловлено появлением в процессе соударения дополнительной

нескомпенсированной составляющей внешней силы – силы реакции

опоры. Однако поскольку реакция опоры не имеет

проекции на гори-

зонтальное направление, сохраняется горизонтальная составляющая им-

пульса системы, (поверхность опоры гладкая и импульсом силы трения

можно пренебречь):

Олимпиада «Ломоносов – 2007»

124

Mum =

v .

Из этих уравнений находим скорости

mM −

vv и

v= .

Теперь можно записать закон движения для каждого из тел после со-

ударения. Направим оси системы координат по горизонтали (Оx) и по

вертикали (Oy). Клин движется равномерно, поскольку трения нет:

uttx =)( .

Движение шарика – равнопеременное:

)(

tty −⋅=

v .

Последние два равенства превращаются в алгебраические уравнения,

включающие искомую величину, если записать их для момента времени

τ=

, когда шарик вернется в ту точку, где он столкнулся с клином:

τ= uS ,

−τ=

v .

Решение записанной системы уравнений позволяет найти ответ:

1022

=≈

−

см.

I.4.

По условию сила сопротивления воздуха v

=F , где v – ско-

рость автобуса,

– коэффициент сопротивления. Поэтому часть мощ-

ности двигателя, расходуемая на преодоление этой силы, равна

vv β== FN . При движении автобуса массой m по наклонному уча-

стку шоссе часть мощности двигателя расходуется также на увеличение

потенциальной энергии автобуса:

v⋅α= sin

mgN . Полная мощность,

развиваемая двигателем,

α+β= sin

vv mgN . Из условия задачи следу-

ет система уравнений:

211

sinsin α+β=α+β=β vvvvv mgmg .

Решения задач

125

Исключая из этой системы

, получаем ответ:

⎟

⎠

⎞

⎜

⎝

⎛

−+= uu

vv , где

sin

sin)(

α−

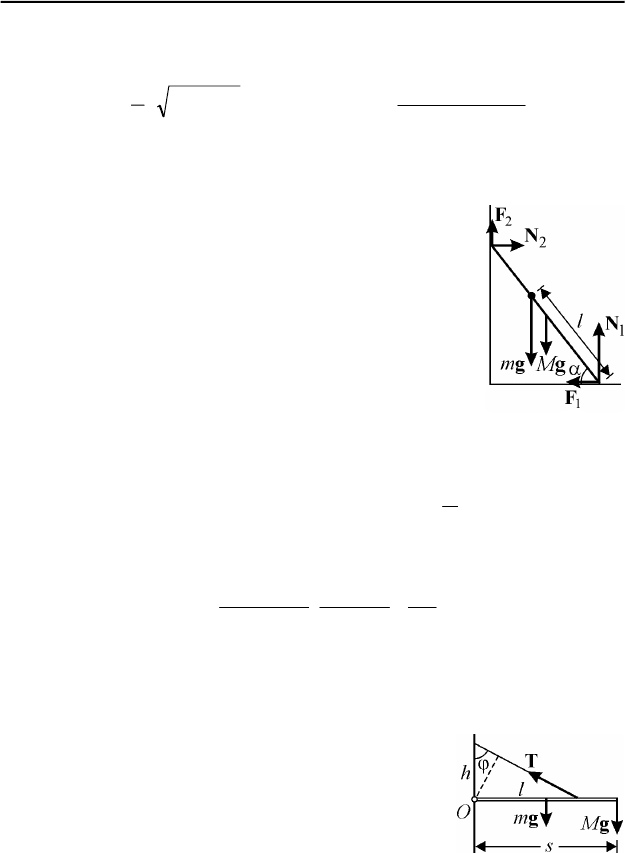
I.5. Стержень находится в равновесии под действием сил, изобра-

женных на рис. 102, где

gm и gM – силы тяжести,

действующие на шарик и на стержень,

N и

N –

нормальные составляющие сил реакции горизонталь-

ной и вертикальной поверхностей,

F и

F – силы

трения покоя. Максимальное расстояние

l соответст-

вует случаю, когда обе силы трения покоя принимают

максимально возможные значения:

= ,

= . Записывая для этого случая условия равно-

весия стержня, имеем:

= , gmMNN )(

+=+

α+α=α+αµ cos

cossincos

MgmglLNLN

Исключая из этих уравнений

N и

N , получаем ответ:

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

+µ

α+µµ

)(

)1(

)tg(

Замечание: Заданные в условии величины m ,

, α и

должны при-

нимать такие значения, чтобы выполнялось неравенство

Ll ≤≤0 .

I.6. Пусть

– масса груза,

– масса стержня,

– его длина. Стержень находится в равновесии под

действием сил, показанных на рис. 103, где

gM и

gm –силы тяжести,

– сила натяжения проволо-

ки. В целях экономии места сила реакции шарнира

на рисунке не изображена. Уравнение моментов,

Рис. 102

Рис. 103

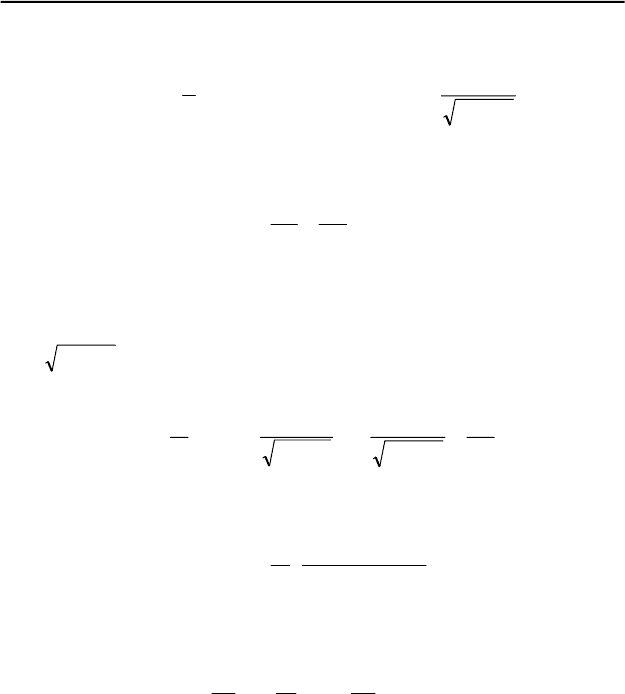
Олимпиада «Ломоносов – 2007»

126

записанное относительно оси шарнира (точки O) имеет вид:

ϕ=+ sin

mgMgs , причем

sin

=ϕ

Пусть

L – длина недеформированной проволоки, а L∆ – ее абсолют-

ное удлинение под действием силы натяжения

. По закону Гука

∆

где

– модуль Юнга, S – площадь поперечного сечения проволоки.

Поскольку проволока жесткая, ее длина в растянутом состоянии мало

отличается от

L . Поэтому можно приближенно положить

hlL +≈ . В итоге уравнение моментов и закон Гука принимают

вид:

Thgs

⎟

⎠

⎞

⎜

⎝

⎛

+ ,

∆

Исключая из этих равенств натяжение проволоки

, найдем ее абсо-

лютное удлинение:

ESl

gsmM

))2/((

⎟

⎠

⎞

⎜

⎝

⎛

+=∆

Минимум этого выражения легко определить, приравнивая нулю произ-

водную

=−=

⎟

⎠

⎞

⎜

⎝

⎛

Отсюда находим ответ:

30== lh см.

I.7. Введем ось Оx, направление которой совпадает с осью стержня.

Поскольку сумма проекций на эту ось всех сил, действующих на шарик

при прохождении положения равновесия равна нулю (пружина не де-

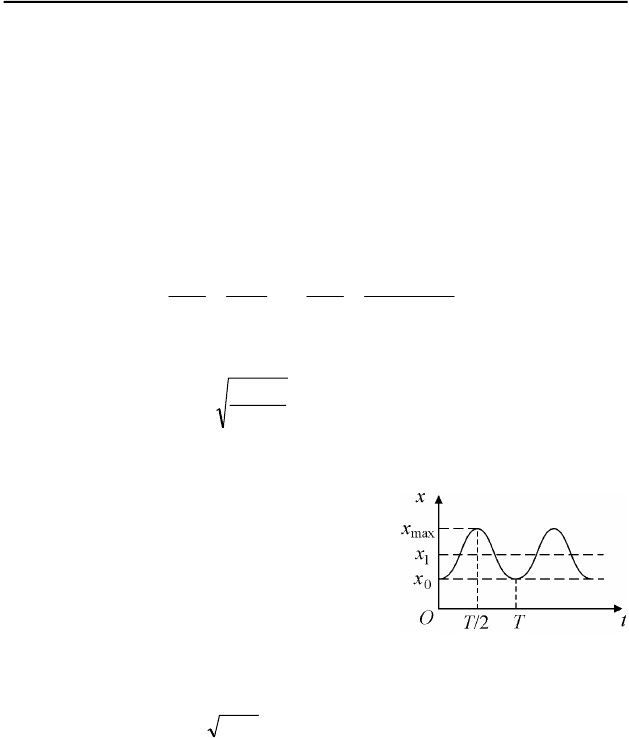
Решения задач

127

формирована, сила трения отсутствует), то можно применить закон со-

хранения импульса для системы «шарик + муха»:

)( umMM +=v ,

где

v – скорость шарика без мухи при прохождении им положения

равновесия,

u – скорость шарика с мухой сразу после ее посадки на

шарик. В процессе колебаний шарика на пружине (или шарика с мухой)

механическая энергия каждой из этих систем постоянна во времени.

Поэтому можно записать:

vMkX

)(

umMkX +

где

k – жесткость пружины. Отметим, что механическая энергия сис-

темы в этих двух случаях различна. Используя записанные уравнения,

получаем ответ:

I.8. Совместим начало системы координат, связанной с кабиной

лифта, с нижним концом недеформирован-

ной пружины; координатную ось Ox напра-

вим вертикально вниз. Когда кабина непод-

вижна, координата гири в положении рав-

новесия равна

kmgx /

= . В момент начала

движения кабины скачком смещается вниз

положение равновесия гири, координата

которой в равновесии становится равной

kagmx /)(

+= . В результате начинаются гармонические колебания

гири с периодом

kmT /2π= . График зависимости координаты гири

от времени

изображен на рис. 104, на котором 0=t соответствует

моменту начала движения кабины. Как видно из рисунка, время

, за

которое длина пружины в первый раз достигает максимального значе-

ния, равно половине периода колебаний гири:

2/T=τ . Путь, пройден-

Рис. 104

Олимпиада «Ломоносов – 2007»

128

ный кабиной за это время,

. Объединяя записанные выражения,

получаем ответ:

I.9. Пусть массы шариков

m и

m , а жесткость пружины k . Часто-

ты колебаний каждого из шариков при условии, что другой шарик за-

креплен, находятся по известной формуле для частоты колебаний груза

на пружине:

=ω ,

=ω .

Если после растяжения пружины отпустить шарики одновременно, то

их колебания будут происходить так, что центр масс системы останется

неподвижным. Обозначим через

x и

x модули смещений шариков от

положения равновесия. Из определения центра масс следует равенство:

2211

xmxm = .

Отсюда находим, что растяжение пружины

xxl +=∆ выражается че-

рез

x и

x как:

=∆

По закону Гука модуль силы упругости, возникающей при растяжении

пружины, равен

lkF ∆= . Уравнения движения шариков имеют вид:

lkxm ∆−=

, lkxm ∆−=

или, с учетом записанных выше выражений для

l∆ ,

+ x

, 0

+ x

Как и следовало ожидать, оба шарика совершают гармонические коле-

бания на одной и той же частоте

Решения задач

129

2121

ω+ω=+=

=ω

Учитывая, что частота колебаний связана с периодом

T соотношением

=ω

, получаем ответ:

II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

II.1. Поскольку поршень вытаскивают из цилиндра медленно (без

ускорения), то внешняя сила нарастает постепенно, оставаясь равной

mgSppF +−= )(

Поршень покинет цилиндр, если сила превысит значение

mgSppF +−= )(

101

где

p – давление воздуха в цилиндре в тот момент, когда поршень дос-

тигает крайнего верхнего положения. В этом положении объем, зани-

маемый воздухом, увеличился по отношению к первоначальному в два

раза. Давление

p определяется, исходя из закона Бойля–Мариотта:

⎟

⎠

⎞

⎜

⎝

⎛

+ .

Совместное решение записанных уравнений позволяет получить ответ:

)(

mgSpF += .

Отметим, что найденное значение силы

F является минимально доста-

точным, для того чтобы медленно вытащить поршень из цилиндра.