Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.

Учет упругопластических деформаций при
изгибе. Программа
plast2
Распределение деформаций при упругопластическом изгибе такое же, как при
упругом изгибе. Распределение напряжений в сечении балки зависит от выбранного
способа аппроксимации диаграммы деформирования. Подробный анализ
напряженно-деформированного состояния балки при изгибе приведен в главе 8.
Характер распределения деформаций и напряжений при упругопластическом изгибе
показан на рис. 8.7.
Рассмотрим численный пример определения напряжений при упругопластическом
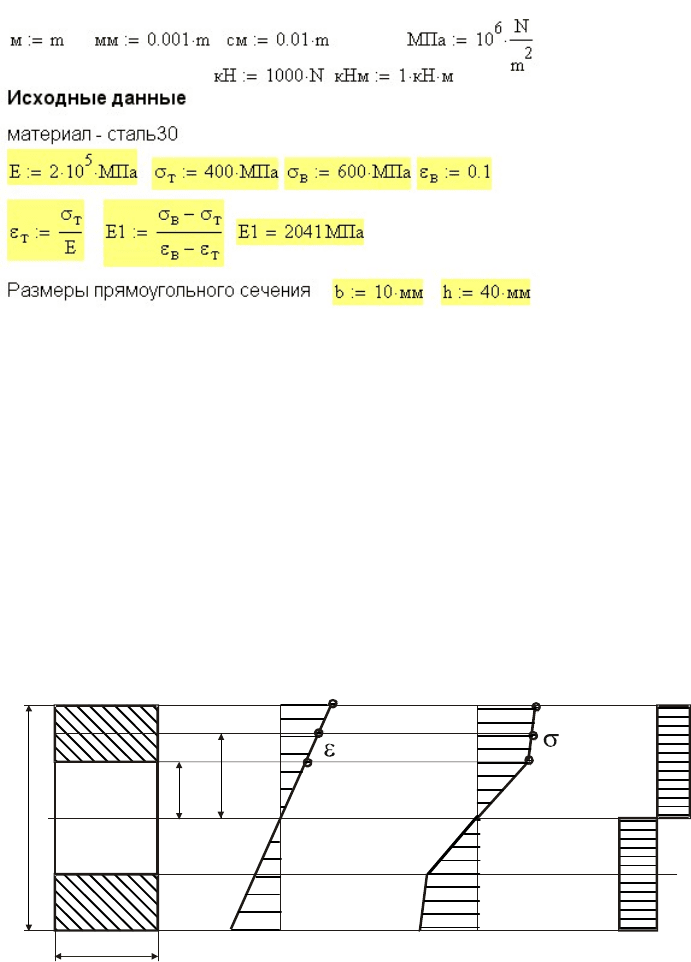
изгибе балки. Исходные данные для расчета приведены на рис. 8.6.
Рис. 8.6 Исходные данные для расчета напряжений при упругопластическом изгибе балки
Характеристики прочности материала взяты из справочника. Деформацией,
соответствующей пределу прочности
в
0,1
ε
≈
задаемся ″на глазок″.
Обратите внимание, что модуль упрочнения
1
E
, равный тангенсу угла наклона
линейной аппроксимации диаграммы деформирования, в 100 раз меньше модуля
Юнга
E
. То есть одно и то же приращение деформации при упругопластической
деформации вызывает приращение напряжений в 100 раз меньшее, чем при упругой
деформации. В этом причина того, что большая ошибка в аппроксимации диаграммы
вызывает маленькую ошибку в распределении напряжений.
Рассматриваем балку прямоугольного поперечного сечения с размерами и .
Длина балки для расчета не имеет значения, так как будем искать не нагрузки на
балку, а изгибающий момент в сечении.
b h
пластическая
зона
h
y
пластический
шарнир
т
ε
max
ε
т
σ
max
σ
т
σ
т
σ
b
упругая
зона
y
т
Рис. 8.7 Распределение деформаций и напряжений при упругопластическом изгибе балки
Задаваясь максимальной деформацией в крайних волокнах балки, определяем
распределение деформаций по высоте сечения балки. Затем, введя аппроксимацию
диаграммы деформирования, определяем распределение напряжений,
соответствующих найденным деформациям.
ПРИМЕЧАНИЕ
Как будет видно из рис. 8.10, в процессе пластической деформации изгибающий
момент изменяется незначительно. Задаваясь им в начале расчета, можно просто не
получить никакого решения, не попав в диапазон изменения изгибающего момента.
Вид аппроксимирующей функции приведен на рис. 8.8, распределение напряжений
по высоте сечения балки в зависимости от принятой аппроксимации диаграммы
деформирования показано на рис. 8.9.
61
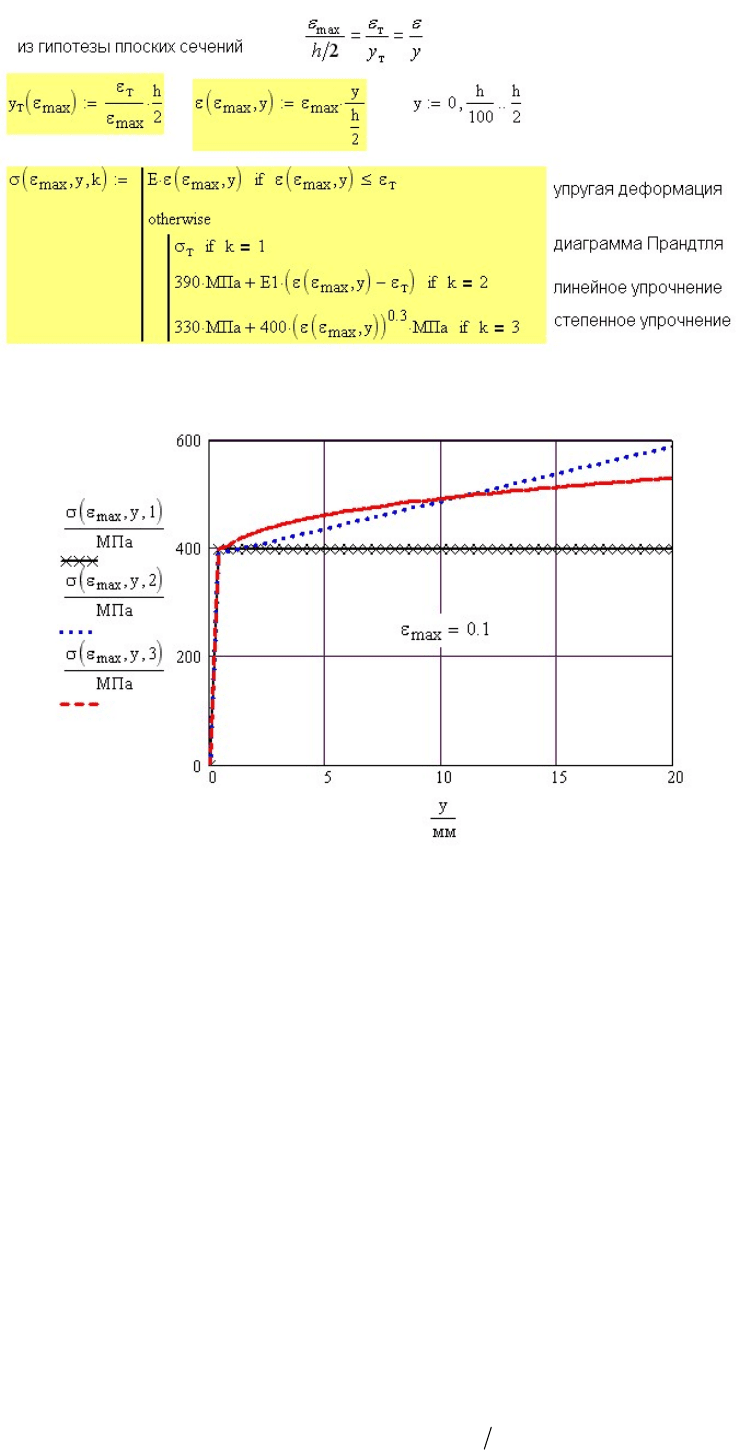
Рис. 8.8 Распределение напряжений по высоте сечения балки
Рис. 8.9 Напряжения в поперечном сечении балки с учетом аппроксимации диаграммы
деформирования
Изгибающий момент в поперечном сечении балки определяем по условию
эквивалентности напряжений и внутренних усилий
A
M
ydA
σ
=
⋅⋅
∫
.
Зависимость изгибающего момента
M
от величины максимальной деформации
max
ε
и вида аппроксимации диаграммы деформирования показана на рис. 8.10.
С ростом
max
ε
величина уменьшается и при
т
y
max
ε
→∞ , но практически
(и теоретически) вблизи нейтральной оси всегда существует упругая зона (пусть и
очень маленькая).
т
0y →
Изгибающий момент при использовании линейной или степенной аппроксимации
диаграммы деформирования медленно растет с ростом
max
ε
. При использовании
диаграммы Прандтля изгибающий момент с ростом пластических деформаций растет
очень медленно, практически оставаясь постоянным.
Такое состояние, когда изгибающий момент практически не растет, а значит
деформация происходит при постоянной нагрузке, называется
пластическим
шарниром
.
Понятие пластический шарнир имеет смысл только при использовании
диаграммы Прандтля.
В нашем примере можно считать, что пластический шарнир уже существует при
max
0,02
ε
= или мм.
т
2y =
На том же рисунке 8.9 сплошной линией показано изменение границы зоны
пластичности от . При
т
y
max
ε
max т
σ
σ
=
т
2yh
=
.
62
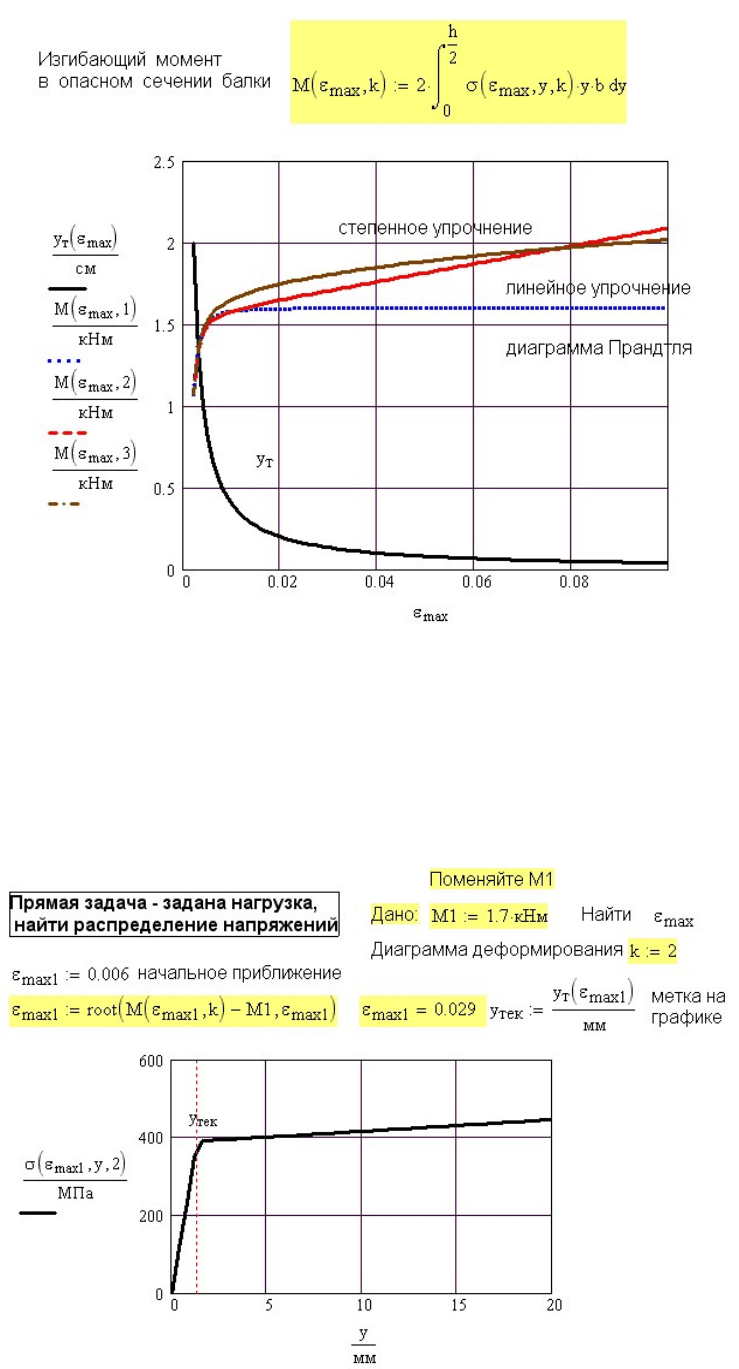
Рис. 8.10. Зависимость размера упругого ядра сечения и изгибающего момента от
деформации
т
y
max
ε
и от вида аппроксимации диаграммы деформирования
Если задан изгибающий момент и надо найти соответствующее ему распределение
напряжений по сечению балки, то надо по графику
max
M
ε
−
найти величину
max
ε
,
соответствующую заданному значению
M
. Затем построить график
σ
от при
найденном значении
y
max
ε
.
Рис. 8.11. Определение распределения напряжений в сечении балки при заданном изгибающем
моменте
Эту же задачу можно решить с помощью функции root (рис. 8.11), предварительно
записав зависимости, приведенные на рис. 8.8 и 8.10.
В пластически деформированной балке при разгрузке возникают остаточные
напряжения. Определим величину остаточных напряжений.
При определении остаточных напряжений следует учесть, что
при нагрузке
распределение напряжений упругопластическое
,
при разгрузке — чисто упругое.
Остаточные напряжения определяются как сумма напряжений нагрузки и разгрузки.
Определение остаточных напряжений при упругопластическом изгибе показано на
рис. 8.12.
63

ост нагр разгр
σ
σσ
=+ .
Рис. 8.12 Определение остаточных напряжений при упругопластическом изгибе балки
Работая с программой, поменяйте значение
max
ε
и посмотрите на характер эпюр и
величину остаточных напряжений.
Учет пластических деформаций при кручении.
Программа
plast3
Распределение деформаций при упругопластическом кручении такое же, как при
упругом кручении. Распределение напряжений в сечении стержня зависит от
выбранного способа аппроксимации диаграммы деформирования. Подробный анализ
напряженно-деформированного состояния стержня при кручении приведен в главе 8.
Характер распределения деформаций и напряжений при упругопластическом
кручении показан на рис. 8.13.
В качестве примера для расчета выбран стержень из стали 30 диаметром 6 мм и
длиной 150 мм, применяемый при лабораторных испытаниях на кручение, что
позволяет сравнить расчетные данные с результатом испытания. Для расчета
использованы результаты испытания этой стали на растяжение (предел текучести
т
σ
, сопротивление разрыву
р
σ
и деформация в шейке при разрыве
р
ε
. Исходные
данные для расчета приведены на рис. 8.14.
d
0
r
Т
r
пластический
шарнир
max
т
τ
т
τ
т
γ
max
τ
Упругая
зона
Пластическая
зона
Рис. 8.13. Распределение деформаций и касательных напряжений в сечении стержня при
упругопластическом кручении
Рис. 8.14. Исходные данные для расчета стержня на упругопластическое кручение
64
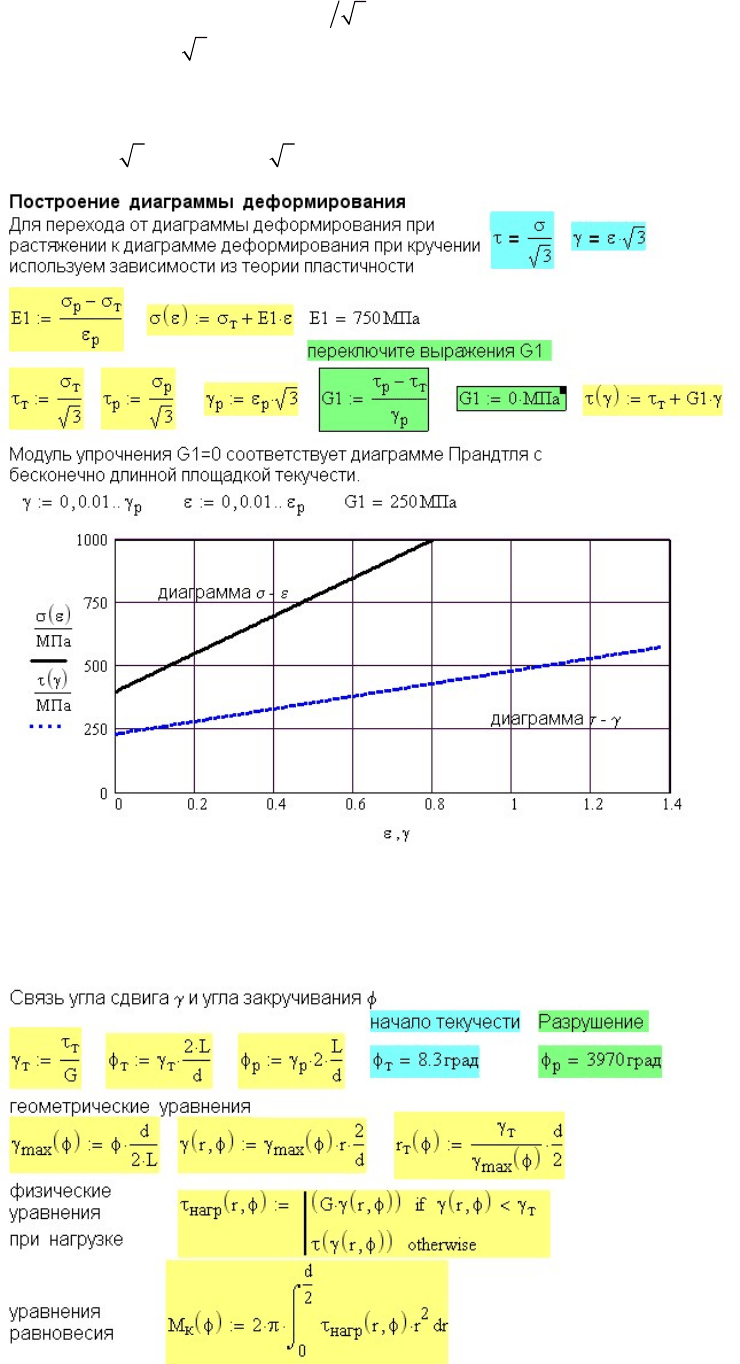
Вначале строим диаграмму деформирования при растяжении. Поскольку заданы
лишь две характеристики прочности, диаграмму деформирования проведем через две
точки, то есть используем аппроксимацию диаграммы деформирования с линейным
упрочнением. Обратите внимание, что модуль упрочнения
1
E
в 300 раз меньше
модуля Юнга
E
(рис. 8.15).
Для перехода к диаграмме кручения запишем связь между касательными и
нормальными напряжениями
3
τσ
= и между углом сдвига и линейной
деформацией
γ
ε
=3. Эти соотношения даются в теории пластичности в
соответствии с четвертой гипотезой прочности (гипотезой Мизеса). Осуществив с
помощью этих соотношений переход от диаграммы растяжения к диаграмме
кручения, строим обе диаграммы (для сравнения) (рис. 8.15). Диаграмма кручения
получается в
3 раз ниже и в 3 раз длиннее.
Рис. 8.15 Диаграммы деформирования при растяжении и при кручении
Далее вводим расчетные выражения (рис. 8.16).
Результаты расчета приведены на рис. 8.17.
Рис. 8.16. Расчет стержня на упругопластическое кручение
В процессе деформации с ростом угла закручивания стержня крутящий момент
быстро растет до появления пластических деформаций, затем рост
к
M
резко
замедляется при линейной аппроксимации диаграммы деформирования и почти
полностью прекращается при использовании диаграммы Прандтля.
65
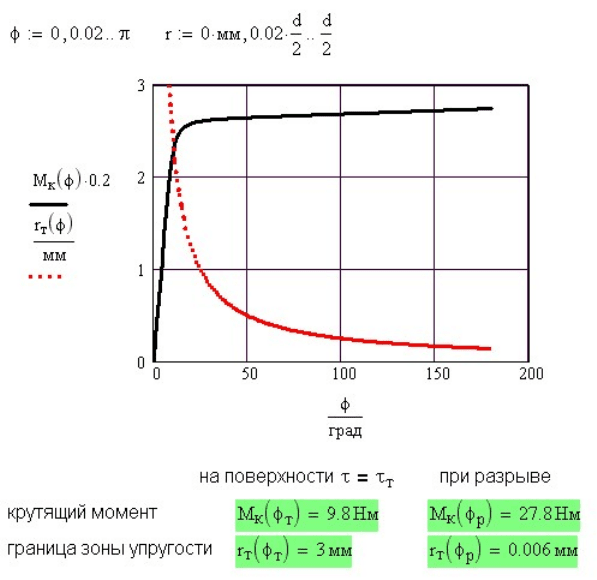
Пластические деформации на поверхности стержня появляются при угле
закручивания
т
10
φ
≈ ° и крутящем моменте
к
10M
≈
Нм. Разрушается стержень при
угле закручивания
р
4000
φ
≈ ° (свыше 11 оборотов) и крутящем моменте
Нм при линейном упрочнении или
кр
28M ≈
кр
13M
≈
Нм при использовании
диаграммы Прандтля.
Рис. 8.17. Зависимость крутящего момента
к
M
и радиуса границы упругой зоны от угла
закручивания стержня
т
r
φ
Определим остаточные напряжения при упругопластическом кручении. Основная
мысль расчета та же, что и при изгибе. Нагрузка — упругопластическая, разгрузка —
чисто упругая.
Остаточные напряжения равняются сумме напряжений при нагрузке и при разгрузке
ост нагр разгр
τ
ττ
=+.
66
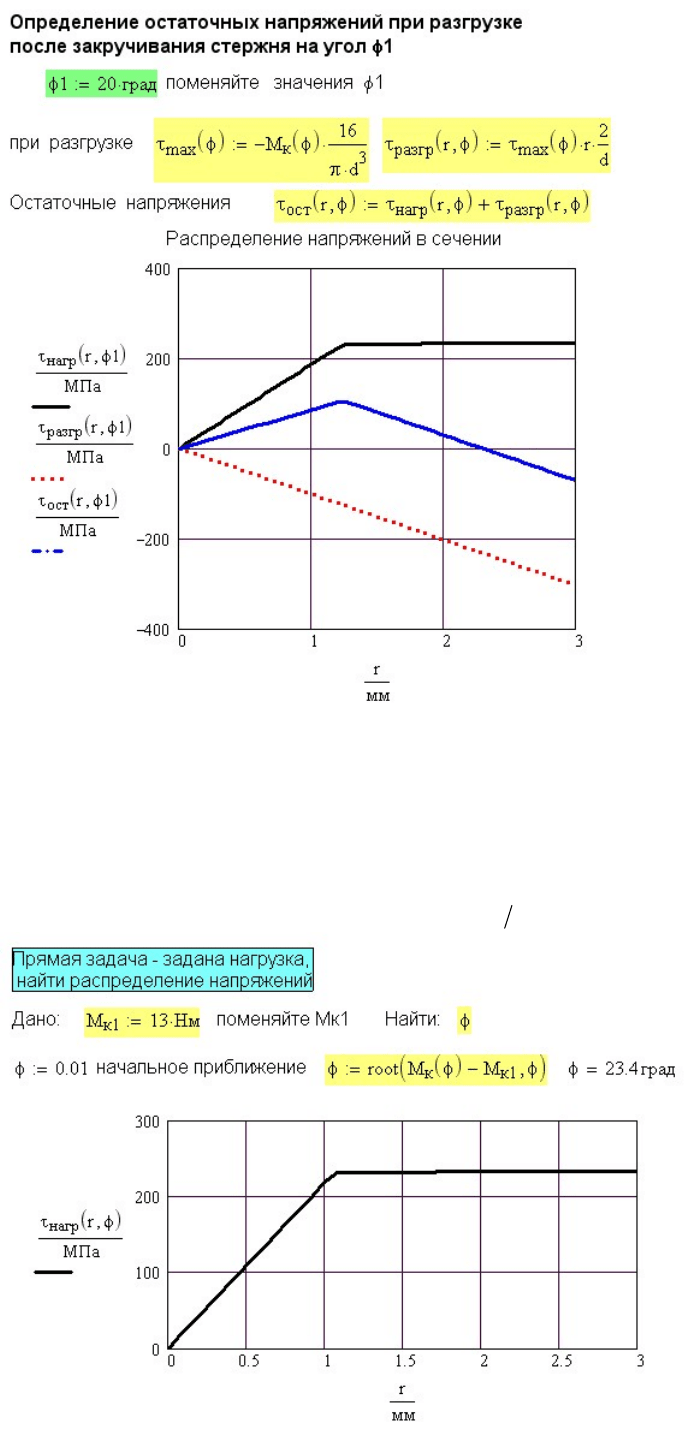
Рис. 8.18. Остаточные напряжения при упругопластическом кручении
При работе с программой переключите выражения для . На рис. 8.15 включено
выражение для линейной аппроксимации диаграммы деформирования. Включите
для использования диаграммы Прандтля и посмотрите на изменение
результатов расчета. Сможете увидеть, что при углах закручивания
1G
1G
10G =
φ
>30°
крутящий момент практически не растет, следовательно образовался пластический
шарнир. При
φ
=
30° упругая зона имеет размер
т max
3rr
≈
мм.
Рис. 8.19 Определение касательных напряжений
τ
при заданном крутящем моменте
к
M
При заданном крутящем моменте можно непосредственно по графику (рис. 8.17),
найти угол закручивания, ему соответствующий.
Задаваться ″на глазок″ крутящим моментом не имеет смысла, так как
упругопластический момент изменяется в очень небольших пределах, и велика
вероятность, что не будет найдено никакого решения.
67
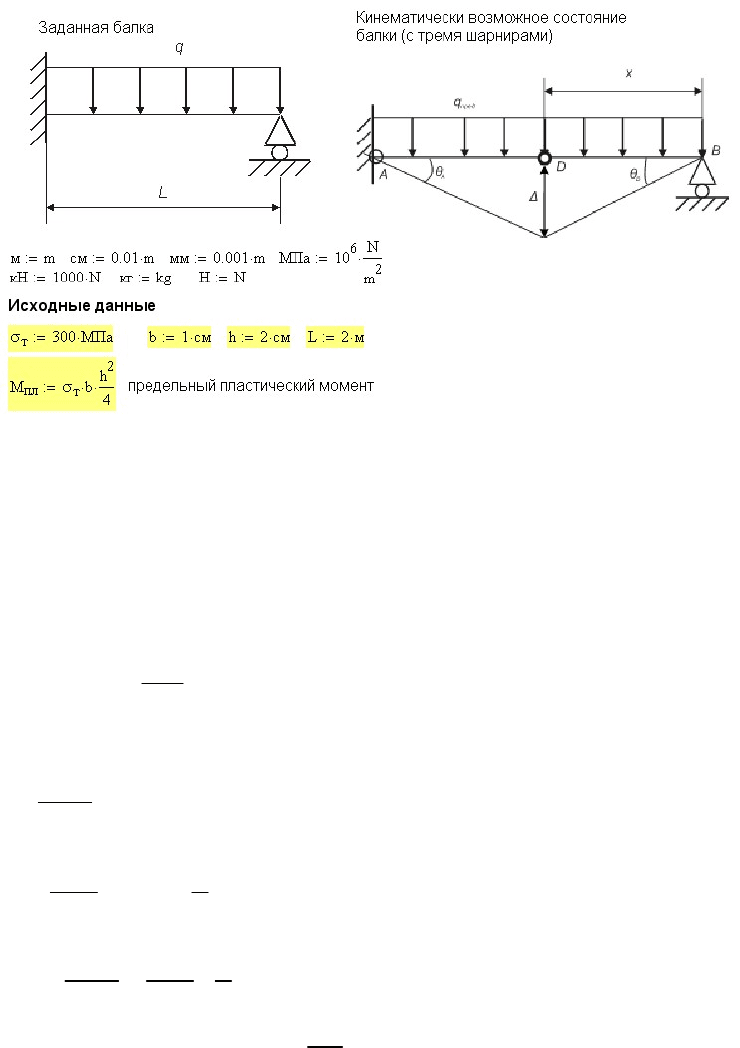
Как показано на рис. 8.19, посмотрев на график (рис. 8.17),можно задаться реальным
значением
к
M
, с помощью функции root определить угол закручивания,
соответствующий этому моменту, и построить эпюру касательных напряжений в
сечении стержня.
Определение предельной нагрузки на балку
методом верхней оценки. Программа
plast4
Статически неопределимая балка (рис. 8.20) нагружена распределенной нагрузкой.
Требуется определить предельную величину интенсивности распределенной
нагрузки. Найдем решение методом верхней оценки.
Рис. 8.20. Кинематически возможное состояние балки
Для различных кинематически возможных состояниях переменными могут быть не
только число пластических шарниров, но и их положение.
В нашей задаче система превращается в пластический механизм при образовании
трех пластических шарниров: в точках А, В и D. Положение шарнира D может быть
различным. Обозначим его положение координатой
x
. Найти положение шарнира D,
при котором предельная нагрузка на балку будет минимальной.
Подсчитаем работы внешних и внутренних сил.
внеш
2
L
Aqq
Δ
⋅
=Ω=
,
()
внутр пл
A
AB
AM
θ
θθ
=++.
Из равенства работ внешних и внутренних сил найдем
()
пл
2
A
AB
M
q
L
θ
θθ
=++
Δ⋅
.
Величина углов
A
θ
и
B
θ
зависит от
x
A
Lx
θ
Δ
=
−
B
x
θ
Δ
=
.
С учетом выражений для углов выражение для предельной нагрузки
q
пл
2
() 2
M
qx
LLxx
ΔΔ
⎛⎞
=+
⎜⎟
−
⎝⎠
.
Для нашего примера
2
пл т
4
bh
M
σ
= — предельный пластический момент в
прямоугольном сечении балки.
68
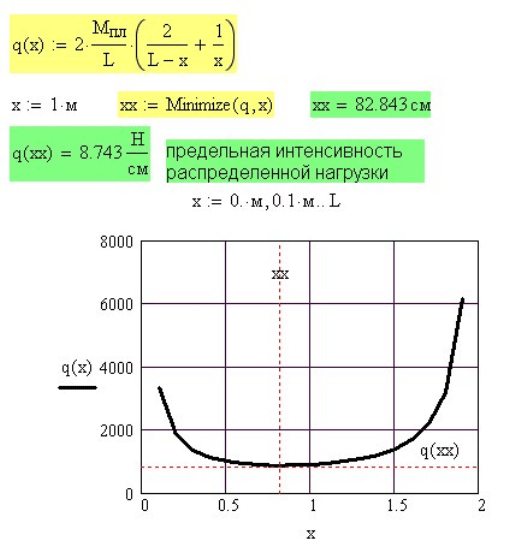
Рис. 8.21. Определение предельной нагрузки методом верхней оценки
Решение задачи в Mathcad показано на рис. 8. 21. На графике зависимости от ()qx
x
виден минимум нагрузки . Это и есть предельная нагрузка на балку. Ее
величину определяем с помощью функции
()qx
minimize, как минимальную предельную
нагрузку в методе верхней оценки.
69
Для главы 10. Примеры расчета стержня
при сложном сопротивлении
Расчет прямого стержня на сложное
сопротивление. Программа
slog-sopr1
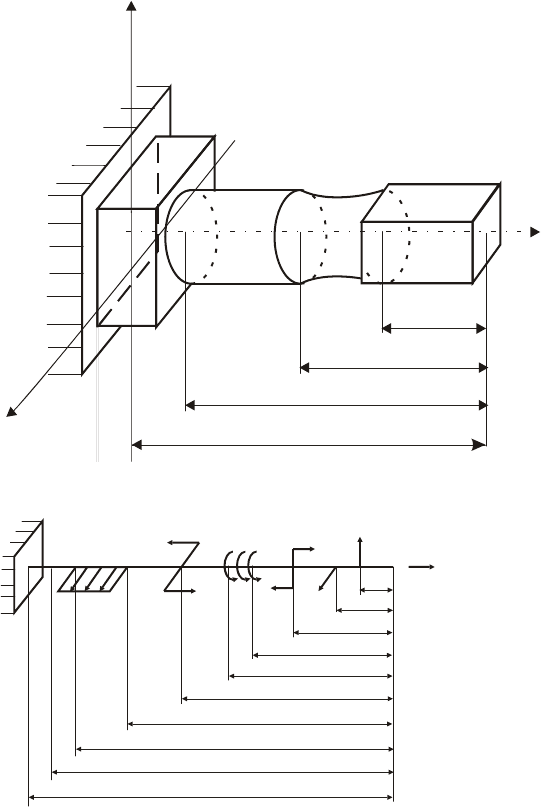
Рассмотрим стержень произвольного сечения, защемленный одним
концом и нагруженный произвольными нагрузками. Форма сечения
стержня показана на рис. 10.1. Условная схема нагружения стержня
приведена на рис. 10.2. Условность схемы состоит в том, что на ней
показаны всего несколько нагрузок, чтобы ввести условные
обозначения нагрузок и координат их точек приложения.
В расчет введено по несколько нагрузок в каждом направлении (число
их может быть любым) в виде векторов. Всего на стержень действуют
23 нагрузки.
X
Z
Y
L
1
L
2
L
3
L
4
Рис. 10.1. Форма сечения стержня
L
Fy
L
Fz
L
Mz
L
mxK
L
mxH
L
My
L
qzH
L
qzK
x
L
q
z
M
y
m
x
M
z
F
z
F
y
F
x
Рис. 10.2. Условная схема нагружения стержня
Исходные данные для определения внутренних усилий приведены на
рис. 10.3. Расчет ведется с учетом размерностей, поэтому перед вводом
данных приведены производные размерности .
70
