Мацко П.В., Голубев А.Г. Введение в геотронику
Подождите немного. Документ загружается.

Число орбитальных
плоскостей
Наклон орбиты к
плоскости экватора
Средняя высота орбит
Период оборота
спутников
55(
20145 км
11 г 58 мин.
64,8(
19100 км
11 г 16 мин.
Сектор управления и контроля. Включает станции слежения, службу точного времени,
главную станцию с вычислительным центром и станции загрузки информации на спутники. В
GPS пять станций слежения распределенные равномерно по земному шару; одна из них
совмещенная с центральной управляющей станцией в Колорадо-Спрінгс (США). Полученная на
этих станциях информация об элементах орбит и прогнозируемые координаты спутников
передается с помощью трех завантажуючих станций на спутники. Существует также и, что не
входит в систему управления и контроля, но более глобальная и точная сеть слідкуючих станций
- Объединенная международная сеть GPS под названием CIGNET (Cooperative International GPS
Network), что находится в ведении Национальной геодезической службы (NGS) США. Созданная
также Международная сеть службы GPS для геодинамики (сеть IGS).
В ГЛОНАСС сеть станций слежения расположена на территории России. Станции
оборудованы радиолокаторами и лазерными віддалемірами, а спутники - отражателями. Под
Москвой расположенный Центр управления системой (ЦУС), который включает центральный
синхронизатор (ЦС) с водородным стандартом частоты.
Сектор пользователя включает спутниковые приемники, число которых и модификации
не ограниченные, а также камеральный комплекс обработки измерений (“постобробки”,
выполняемой после полевых наблюдений).
Режимы работы систем. Глобальные спутниковые системы могут работать в двух
основных режимах, которые получили название кодовых измерений и фазовых измерений. При
кодовых измерениях выполняется измерения времени распространения кодово-модулированного
сигнала от спутника до приемника, а при фазовых - измерение смещения фазы колебания
несущей частоты за время распространения. Следует отметить, что для этих режимов часто
используют другие названия, которые характеризуют их, так сказать, с другой стороны. Режим
кодовых измерений называют навигационным, а также абсолютными определениями, а режим
фазовых измерений - геодезическим, а также относительными определениями. Такая терминология
используется потому что кодовые измерения дают меньшую точность, приемлемую при решении
задач навигации, и при этом обеспечивают непосредственное получение самых координат
( абсолютных величин). Фазовые же измерения дают высокую точность, пригодную для
геодезической цели, но при этом позволяют получить не самые координаты, а различия
одноименных координат двух (или более) точек, в которых установленные одновременно
работающие приемники.
Иногда в отдельный (третий) режим выделяют так называемый интегральный
допплерівський счет, который осуществляется, по сути дела, одновременно с режимом фазовых
измерений. Он позволяет получать скорость изменения расстояния к спутнику и фиксировать
моменты последовательных положений спутника.
Все три указанных режимы будет рассмотрено дальше.
ВОПРОС ДЛЯ САМОКОНТРОЛЯ:
1. Дайте короткое определение понятием: созвездие спутников, наземные станции
контроля, спутниковые приемники?
2. В чем заключається основная функция станций слежения?
3. Укажите число орбитальных плоскостей и число спутников каждой плоскости в GPS?
4. Что представляет собой режим кодовых измерений?
5. Что представляет собой режим фазовых измерений?
6. Какие измерения более точные?
7. На скольких частотах излучается колебания каждым спутником?
8. Какой вид модуляции несущих колебаний используется в спутниковом сигнале?
9. Что такое фазовая манипуляция?
10. В какие моменты происходит фазовая манипуляция?
11. Что модулируется грубым и точным кодом?
6
7.2. Спутниковый сигнал
Сигнал, который передается из спутника являются излучаемыми в пространство
электромагнитными колебаниями на двух несущих частотах, означают L1 и L2, подвергнутых
особому виду фазовой модуляции - фазовой манипуляции. Последняя состоит в перебрасывании
фазы несущей на 180
в
в определенные моменты. Эти моменты задаются так называемыми
віддалемірними кодами - определенными последовательностями нулей и единиц. Перебрасывание
фазы происходит в моменты изменения в кодах 0 на 1 или 1 на 0 (рис.7.2).
Таких кодов используется два: один для "грубых", другой для " точных измерений", и они
существенным образом различаются, о чем будет подробнее сказан ниже. Грубым кодом
модулируется несущая L1, а точным кодом - обе несущих L1 и L2. В GPS грубый код называется
С/ А-Кодом ( от слов Coarse Aquisition - что легко находится, общедоступный), а точный – Р-
Кодом (Precision - точный). С/ А-Код предназначен для всех пользователей.Р-Код сначала
назначался только для тех, что имеют санкционированный доступ ( в основном для американских
военных). Сейчас доступ к Р-Кода имеют приемники практически всех пользователей. В системе
ГЛОНАСС аналогичная ситуация, различие только в названиях: грубый код называется Ст-Кодом
(кодом стандартной точности), а точный код - Вт-Кодом (кодом высокой точности). Однако
между GPS и ГЛОНАСС есть принципиальное отличие, которое относится к использованию
кодов. В GPS как С/ А-Код, так и Р-Код резни для каждого спутника при сходства несущих частот
L1 и L2 для всех спутников системы. В ГЛОНАСС же, наоборот, коды СТ и ВТ всех спутников
одинаковые, но разные несущие частоты. Другими словами, в GPS примененное кодовое, а в
ГЛОНАСС - частотное разделение сигналов от каждого спутника.
Применение кодов решает задачу измерения расстояний (псевдодальностей) временным методом
с использованием корреляционной обработки сигнала. Как это делается, будет рассмотрен в
следующем разделе. Но спутниковый сигнал подвергается не только кодовой модуляции,
необходимой для измерения расстояний. У него "встраивается" вся информация из спутника,
который передается - мотки времени, данные об эфемериды спутника, разные поправочные
величины, альманах (сборник менее точных данных о местонахождении каждого из спутников
системы и состояние его “здоровье”) и др. Вся эта информация, создает навигационное
сообщение, также превратится в двоичный код (последовательность нулей и единиц), которым
дополнительно модулируются обе несущие частоты. Модуляция осуществляется так же, как и
віддалемірними кодами - перебрасыванием фазы несущего колебания на 180° в моменты изменения
символов (нулей и единиц). Частота прохождения символов навигационного сообщения
составляет 50 Гц(или, как то говорят, информация передаться со скоростью 50 бит/с, поскольку
один символ - 0 или 1 - содержит один бит информации).
Таким образом, сигнал каждого спутника в обеих рассмотренных глобальных системах
составляется с двух несущих колебаний разных частот, маніпульованих за фазой как
дальномерными кодами, так и навигационным сообщением. Дальнейшее рассмотрение этот
вопроса будет ориентировано в основном на систему GPS как на ту, что получила более широкое
применение у пользователей.
6
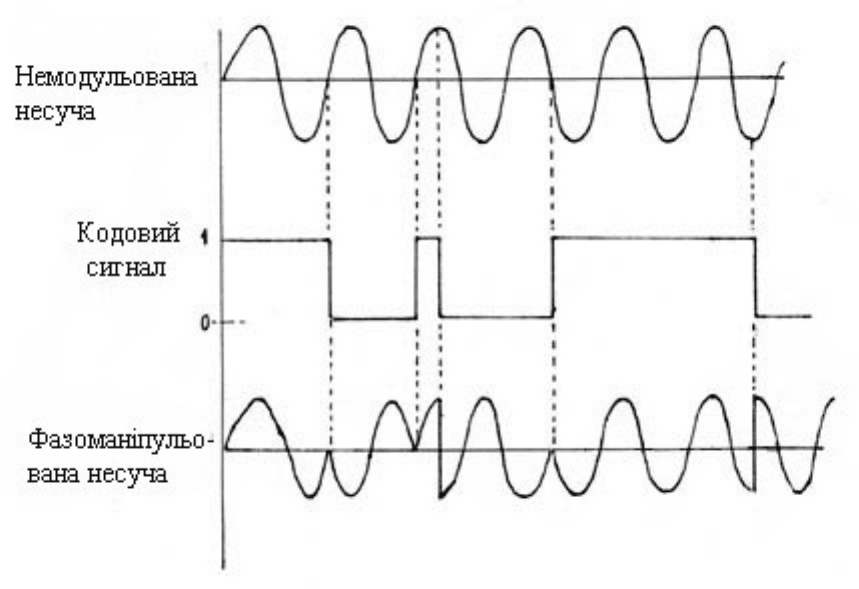
Рис.7.2. Фазовая манипуляция под действием кодового сигнала
На спутниках GPS високостабільний опорный кварцевый генератор, стабилизированный с
помощью атомных эталонов частоты, генерирует колебание с частотой 10,23 Мгц, с которых
соответствующим умножением или делением синтезируется вся остальные частоты – несущие,
частоты прохождения символов С/А- и Р- кодов и символов навигационного сообщения. Номиналы
всех частот и образ их получения указаны в таблице 7.2.
Таблица 7.2
6
Віддалемірні коды. Віддалемірним кодом называют последовательность сигналов,
которые могут находиться в двух разных состояниях, которым условно приписывают значение
(символы) 0 и 1. Эти состояния принудительно дежурят таким образом, который у них
изменению невозможно заметить какой-нибудь закономерности, то есть дежурство выглядит
случайным, но через определенные интервалы времени оно периодически повторяется с
точностью до каждого символа. Подобные последовательности называются псевдослучайными и
образовывают псевдослучайные коды. На спутнике и в приемнике генерируются абсолютно
одинаковые коды, которые окажутся смещенными по времени. Период повторения
псевдослучайных последовательностей (продолжительность кода) существенным образом
различается для “грубого и “точного” кодов”. Так, в GPS C/ A-Код повторяется каждую
мілісекунду, а продолжительность Р-Кода составляет 266,4 суток. Короткая
продолжительность C/ А-Кода позволяет легко захватить сигнал спутника на частоте L1.
Намного труднее осуществить увлечение спутникового сигнала на несущей L2, которая
модулирована только Р-Кодом. Его чрезвычайно большая продолжительность выбранная
разработчиками специально с целью утруднять доступ к нему для несанкционированных
пользователей. Общая продолжительность Р-Кода разбитая на недельные отрезки,
распределенные по всем спутникам системы, то есть Р-Код каждого спутника меняется через
неделю. Разработчиками GPS были предусмотрены введения режима избирательного доступа (SA -
Selective Availability), при которому с целью снижения точности измерений нарочно вносятся
искажения в віддалемірний код и загрубляється ефемеридна информация в навигационном
сообщении (в данное время, однако, режим SA отменен).
Для создания еще большей защищенности Р-Кода вводится режим дополнительного
шифрования - так называемое Y-Кодирование (режим AS - Anti-Spoofing, что буквально
переводится как “противодействие попытке обмана”).Y-Код математически может быть описан
умножениям Р-Кода на нелинейную функцию W(t), неизвестную несанкционированным
пользователям. Фактически Y-Кодирования - это обмен недельными отрезками Р-Кода в
последовательности, известной только персонала системы. Правда, в данное время фирмы-
производители приемочной аппаратуры добились на коммерческой основе разрешения вводить в
компьютер приемника соответствующую микросхему, которая реализовывает алгоритм
отыскания функции W(t).
Навигационное сообщение содержит 1500 бит и занимает 30 секунд. Оно разделено на 5
субкадрів по 300 бит, каждый с которых передается на протяжении 6 секунд. Субкадр
составляется с 10 слов по 30 бит.
Каждый субкадр начинается с телеметрического слова TLM (Telemetry Word), что
содержит диагностическое сообщение о состоянии спутника. Вторым словом каждого субкадру
есть так называемое ключевое слово, обозначается HOW (Hand-over Word, буквально - “слово,
которое передается из рук в руки”). Это слово содержит метку времени ( так называемый Z-
Отсчет), записанную в виде 29- разрядного числа в двоичном коде.
Сдача информации распределяется по субкадрах таким образом:
Субкадр 1 содержит данные о поправке часов спутника относительно системного
времени GPST и коэффициенты, заложенные в модель задержки радиосигнала при прохождении
его через ионосферу. Информация об ионосфере предназначена только для абонентов, которые
используют одночастотные приемники (принимающие только частоту L1). При наличии
двочастотного приемника влияние ионосферы практически исключается так называемым
дисперсионным образом
Субкадри 2 и 3 содержат эфемериды транслюючого спутника, полученные по данным
наземных станций слежения. Они корректируются каждый час, но остаются в силе на
протяжении еще некоторого дополнительного интервала времени ( по крайней мере на
протяжении полчаса) и позволяют вычислить текущие координаты спутника на момент
измерения псевдодальності. Эфемериды включают элементы кеплерової орбиты (см. курс
6
астрономии или космической геодезії) на опорный момент и поправки к ним, которые позволяют
прогнозировать элементы орбиты внутри периода действия эфемерид.
Субкадр 4 зарезервированный для передачи информации служебного характера и
приемники гражданских пользователей лишены возможности ее получения.
Субкадр 5 содержит альманах спутников и данные о них трудоспособность. Альманах -
это приблизительные эфемериды всех спутников системы. Альманах используется для
планирования измерений.
Информация, которая спорит в субкадри 4 и 5, не помещается в одном навигационном
сообщении, и эти субкадри разделенные на 25 страниц. В каждом сообщении передается одна из
этих страниц, так что на передачу всей информации 4-го и 5-го субкадрів затрачивается 30
с( 25 = 750 с = 12,5 мин.
ВОПРОС ДЛЯ САМОКОНТРОЛЯ:
1. Что, кроме віддалемірних кодов и несущих частот, входит в спутниковый сигнал?
2. Что модулируется навигационным сообщением?
3. Что представляют собой віддалемірні коды?
4. В котором субкадрі передается метка времени?
5. Сколько времени тратится на передачу альманаха?
6
Раздел 8. МЕТОДЫ СПУТНИКОВЫХ ИЗМЕРЕНИЙ
8.1. Кодовые измерения
При кодовых измерениях, как уже подчеркивалось раньше, величиной, которая измерится,
есть время
распространение сигнала от спутника до приемника, в которое входит как задержка
в атмосфере, так и совокупное отклонение часов спутника и приемника от системного времени.
Измерения выполняются путем корреляционной обработки кодовых сигналов.
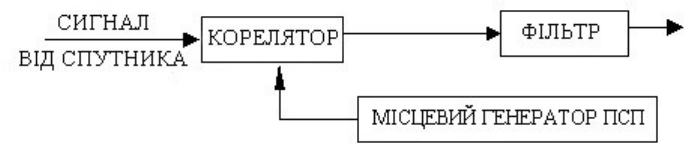
Принцип кодовых измерений иллюстрируется на рис.8.1. В приемнике формируется точно
такой же псевдослучайный код, которым модулирован спутниковый сигнал.
Рис.8.1. К принципу кодовых измерений с корреляционной обработкой сигнала
Этот код (назовем его местным кодом) и сигнал, который приходит от спутника
подаются на корелятор, который обеспечивает переворот фазы несущего колебания, которое
приходит, на 180
в
в моменты изменения символов местного кода. Тогда, если менять задержку
местного кода относительно кода, который содержится в спутниковом сигнале, то, когда эта
задержка станет равной нулю, на выходе корелятора возникнет не модулированное колебание
несущей частоты. Поэтому, при співпаданні обеих кодов до 180 в-
их
сдвигов фазы несущей от “
спутникового кода” будут в те же моменты добавляться 180 в-
ни
сдвиги от местного кода, а
значит, общий сдвиг фазы несущей будет 360
в
(нулевой), то есть фазовая манипуляция
снимается. При этом мощность сигнала на выходе фильтру резко возрастает (что отвечает
максимуму корреляционной функции).
Таким образом, появление немодулированного колебания служит индикатором совпадения
“спутниковой и местной кодовых последовательностей”, которые были сдвинуты во времени.
Эта временная задержка и измеряется при сдвиге местного кода относительно спутникового к
ним співпадання. Здесь, однако, надо иметь в виду, который если мы работаем за грубым кодом
(С/ А-Кода в GPS или Ст-Кода в ГЛОНАСС), то мы можем таким образом измерить задержку
только в пределах периода повторения кода, который составляет в обеих системах 1мс. Чтобы
получить полное время распространения, надо знать, сколько в нем содержится целых мілісекунд.
Поскольку за 1 мс радиоволна проходит 300км, то надо знать, сколько 300- километровых
отрезков содержится в расстоянии к спутнику, то есть знать это расстояние с ошибкой меньше
150км. Для этого достаточно вычислить ее за координатами спутника и приближенных
координатах наземной станции.
При использовании точного кода такой проблемы не возникает, поскольку его период
повторения явным образом больше времени распространения
.
Определивши
и помножив его на скорость света в вакууме, получают псевдодальність,
описываемую формулой (6.2) раздела 6:
Р =
+ с
t
атм
+ с
t
г
.
Определение координат из кодовых измерений. Запишем полученную из кодовых
измерений псевдодальність в виде:
Р =
+
т
+
и
+ с
t
г
, (8.1)
где члены
т
и
и
- выраженные в линейной мере суммарные “взносы” тропосферы и ионосферы
соответственно, обусловленные как задержками, так и удлинением рефракции траектории. Эти
величины могут быть учтены (вычисленные) с определенной степенью точности (см. следующий
раздел), то есть их можно считать известными. Неизвестными остаются
и
t
г
.
Дальность
связанная с геоцентрическими координатами приемника X,Y,Z и спутника XS,
YS
,
ZS известным из аналитической геометрии соотношением:
= [(XS - X)
2
+ (YS - В)
2
+ (ZS - Z)
2
]
1/2
(8.2)
Координаты спутника XS, YS
,
ZS получают по ефемеридними данным, которые с помощью
сектора управления и контроля спорят в навигационное сообщение, транслированное из
спутника на приемник, то есть XS, YS
,
ZS можно считать известными. Поэтому уравнение (8.1)
фактически содержит четыре неизвестных - три координаты приемника ( определяемого
пункта) X,Y,Z и относительный отход часов
t
г.
Если выполнить ОДНОЧАСНО измерение
псевдодальностей до четверых спутников, то мы получаем ( об этом уже упоминалось раньше)
6
систему четверых уравнений вида (8.1) с четверыми неизвестными, из решения которых и
находятся искомые координаты пункта X,Y,Z.
Дифференциальный метод кодовых измерений. Описанным выше образом, который
иногда называют автономным, можно было получать координаты с погрешностью в диапазоне
10-100 м, но после отличия режима избирательного доступа (SA) погрешность снизилась до 5-15
г. Существенным образом увеличивается точность при использовании так называемого
дифференциального метода. Это - метод с использованием двух наземных станций (приемников).
Одна из них устанавливается на пункте с известными координатами и называется базовой,
опорной или референц-станцией. Другая станция есть подвижной (роверною). Приемник базовой
станции беспрерывно работает в Р-Коде, и вымеренные им псевдодальності сравнивают с
“эталонными расстояниями”, вычисленными за координатами. Получаемые различия, которые
называют дифференциальными поправками, передают на передвижной приемник для коррекции
измерений. При этом предполагается, что много погрешностей одинаково влияют на измерение с
обеих станций. Чем меньше расстояние между станциями, тем это предположение выполняется
точнее. Например, при расстояния меньше 10 км влияние атмосферы можно считать абсолютно
одинаковым - радиоволны от спутника, который находится на высоте 20 000 км, проходят
расстояния до двух что разнесли на 10 км приемников практически в одних и тех же атмосферных
условиях.
Дифференциальный метод выводит точность кодовых измерений в диапазон от
нескольких метров до нескольких дециметров. Существует целая сеть базовых станций ( в
разных странах), что передают дифференциальные поправки в стандартном международном
формате для всех заинтересованных пользователей (бесплатно или на коммерческой основе).
ЗАПИТАНННЯ ДЛЯ САМОКОНТРОЛЯ:
1. В которых дальномерах метод с одноразовым прохождением сигнала вдоль трасы?
2. Как определяется временная задержка при кодовых измерениях?
3. При работе на каком коде отсутствующая неоднозначность?
4. Какие неизвестные величины в уравнении для псевдодальності?
5. На каком расстоянии повина устанавливаться базовая станция при дифференциальном
методе кодовых измерений?
6. Какое расстояние (в км) проходит радиоволна за период повторения грубого кода в GPS
и ГЛОНАСС?
7. В системе ГЛОНАСС расстояние до одного со спутников в момент измерения
составляла 20200 км. Сколько целых периодов Ст-Кода содержится во времени
распространения сигнала?
8. Сколько неизвестных величин в уравнении для псевдодальності?
8.2 Фазовые измерения.
Интегральный допплерівський счет
Обратимся теперь к геодезическому режиму работы глобальных систем - фазовым
измерением на несущей частоте. В этом случае измеряется не время распространения сигнала
от спутника до приемника, а сдвиг фазы колебаний несущей частоты (излучаемой спутником) за
это время, но - и это создает главную проблему - не полный сдвиг
SR
, связанный с расстоянием
от спутника S к приемнику R, а лишь его дробовая часть, меньшая 2
. Это та же проблема
решения неоднозначности, которая возникает и в наземных фазовых віддалемірах. Сдвиг
измеренных фаз реализуется в приемнике как различие фаз между сигналом, принятым от
спутника, и опорным сигналом, который генерируется в приемнике. Предположим, что для
некоторого фиксированного момента времени мы измерили дробовую часть фазового сдвига
.
Но, чтобы определить расстояние, нам нужный полный фазовый сдвиг, который равняется
SR
= 2
N +
=
= 2
f (P/c) (8.3)
где N - неизвестное целое число, f - несущая частота, Р - псевдодальність, что содержит
геометрическое расстояние
. С формулы 8.3 легко получить Р, учитывая, что с/f =
(длина
волны в вакууме):
Р =
N +
(
/2
). (8.4)
Это почти та же псевдодальність, что и при кодовых измерениях, и ее можно
представить выражением вида (6.2), но с двумя характерными отличиями. Во-первых,
ионосферный член
и
при фазовых измерениях будет иметь другой знак (см. следующий раздел ). А
во-вторых, величина
t
г
, которая фигурирует в (6.2), будет иметь кое-что другое трактование.
6
При кодовых измерениях она отображает несинхронность хода часов спутника и приемника. При
фазовых же измерениях она является следствием несинфазності (неспівпадання начальных фаз)
колебаний опорных генераторов спутника и приемника, которую мы будем обозначать через
d
.
Именно наличие величины
d
приводит к тому, что мы и из фазовых измерений получаем
псевдодальність. Понятно
t
г
и
d
жестко связанные друг с другом (
d
= 2
f ·
t
г
), оскільки,
внаслідок єдності еталона часу і частоти, “годинник” - це і є генератори коливань.
В литературе часто употребляют выражения “кодовая
псевдодальність” и “фазовая псевдодальність”. Добавим им индексы “к”
и “ф” и запишем, с учетом сделанных замечаний, в виде:
Р
к
=
+
т
+
и
+ с
t
г
(8.5)
Р
ф
=
+
т
-
и
+ c(
d
/2
f). (8.6)
Приравнивая (8.4) и (8.6), определим величину
/2
, обозначая ее через Ф (вымеренная
величина различия фаз, выраженная в частицах цикла - то, что в наземной фазовой віддалеметрії
обозначают как
N):
Ф = (
/
) - N + (
т
/
) - (
и
/
) + (
d
/2
) . (8.7)
Присутствие неизвестного целого числа N приводит, как уже упоминалось, к проблемы
решения неоднозначности.
Обычно в литературе уравнения фазовых измерений используют в виде (8.7).
Если мы каким-то чином определили число N, то можно получить вымеренное значение
фазовой псевдодальності Рф. Однако она содержит неизвестную величину
d
. Фазовые измерения
с двумя приемниками позволяют исключить эту величину, используя так называемый метод
фазовых различий.
Метод фазовых различий. Для исключения
d
достаточно выполнить измерение не до
четверых, как при кодовых измерениях, а только до двух спутников. Величину
d
можно
представить различием
d
S
d
R
( то есть различием начальных фаз колебаний генераторов на
спутнике и в приемнике). Если выполнить наблюдение одного и того же спутника одновременно
двумя приемниками, которые разнесены на некоторое расстояние (в пункты А і В), то в различии
двух уравнений вида (8.7) исключается величина
d
S
для наблюдаемого спутника.
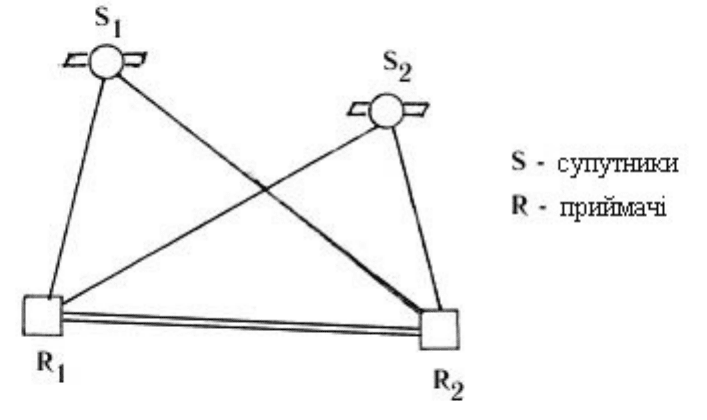
Рис.8.2. Геометрия наблюдений для получения второго фазового различия
Если выполнить теми же приемниками и в ту же эпоху наблюдения второго спутника, то в
различии исключается величина
d
S
для этого второго спутника. Если теперь составить
различие различий - так называемую другу различие (обозначим ее
Ф
II
), - то исключается
величина
d
R
для обеих приемников. Геометрия измерений показана на рис.8.2.
Таким образом, во втором различии ликвидируется крупный недостаток одностороннего
(беззапитного) фазового метода – неизвестное отличие начальных фаз колебаний на спутнике и
в приемнике. Тому спосіб вторых различий есть основным при точных геодезических измерениях.
Однако этот образ не ликвидирует другого крупного недостатка фазовых измерений -
необходимости решения неоднозначности.
Отметим, что если повторить вышеописанную процедуру наблюдения двух спутников
двумя приемниками в другой момент времени, то есть когда эти спутники займут другое
положение, и так же получить другу различие, а потом составить различие вторых различий –
третье различие (
Ф
III
), то неоднозначность, как часто говорят, исключается. На самом деле это
6
не так: неоднозначность в этом случае не исключается, а, так сказать, игнорируется. Суть дела
здесь заключается в том, что при образовании третьего различия у нее входят не самые
расстояния между спутниками и приемниками, а их прирастить за время перемещения спутников
по орбите. Соответственно в третьем различии фигурируют не неизвестные значения N
фазовых циклов, а их прирастить
N. Эти приросты могут измеряться за показателями
фазометричного устройства при беспрерывному відстежуванні сигнала спутника. Нахождение же
целых чисел N ( по всем расстояниям), которые имеют порядок
108
и должны быть
определенный с точностью до единицы, является исключительно сложной задачей. Полагает,
что неоднозначность решена, если точно определенные целые числа No = (NA – NB)
S1
– (NA –
NB)
S2
, фігуруючі во вторых различиях. Процесс определения No называют инициализацией.
Существует несколько возможных образов определения Nо. Однако в процессе наблюдений
оператор не может взнати, решенная ли многозначность - он узнает об этом только после так
называемой постобробки, осуществляемой на офисном компьютере, на который перекачиваются
все данные, полученные во время работы спутникового приемника.
Фазовые измерения, как основа относительного метода. Если многозначность решена,
то другу фазовое различие
Ф
II
можно перевести в линейную меру (умножением на длину волны
).
Это будет второе различие фазовых псевдодальностей, что содержит величины
А
1
,
В
1
,
А
2
,
В
2
- геометрические расстояния от приемников А і В к спутникам 1 и 2. Обозначим указанную другу
различие фазовых псевдодальностей через Р
12
. Она связана с координатами двух спутников (X
1
, Y
1
,
Z
1
), (X
2
, Y
2
, Z
2
) и приемников (Х
А
, У
А
, ZA), (XB, YB, ZB) соотношением:
Р
12
=
(X
1-XA
)
2
+ (Y
1-YA
)
2
+ (Z
1-ZA
)
2
1/2
-
-
(X
1-XB
)
2
+ (Y
1-YB
)
2
+ (Z
1-ZB
)
2
1/2
-
-
(X
2-XA
)
2
+ (Y
2-YB
)
2
+ (Z
2-ZB
)
2
1/2
+
+
(X
2-XB
)
2
+ (Y
2-YB
)
2
+ (Z
2-ZB
)
2
1/2
+
d
а
12
(8.8)
где последний член есть “двойное различие атмосферных задержек”, что отображает
остаточное влияние атмосферы на трасах распространения сигналов от спутников 1 и 2 к
пунктам А і В.
Поскольку координаты спутников известные, то в (8.8) остаются неизвестными
координаты пунктов А і В. Если мы выполним на пунктах А і В соответствующие наблюдения
(измерение фазовых псевдодальностей Р
ф
) до ЧЕТВЕРЫХ спутников ( то есть как и в случае
кодовых измерений), то получим три независимых уравнения вида (8.8): для Р
12
, Р
13
и Р
14
, в
которых в качестве неизвестных будут выступать три РАЗЛИЧИЯ одноименных координат
пунктов А і В - конечных точек базовой линии: (XA-XB), (YA-YB) и (ZA-ZB), которые и
определяются из решения системы уравнений
.
Если один из приемников поместить в пункте с
известными координатами (что обычно и делают), то за полученными различиями легко
находятся координаты второго пункта.
По различиям координат можно вычислить и расстояние между приемниками (длину базы):
АВ =
(XA-XB)
2
+ (YA-YB)
2
+ (ZA-ZB)
2
1/2
. (8.9)
Точность фазовых измерений существенным образом превосходит точность кодовых
измерений и составляет в среднем
(5-10) + (1-2)D
мм, где D - длина базы в километрах. По
высоте точность выходит кое-что меньше чем в плане.
Восстановление несущей частоты при фазовых измерениях. В подразделе “Кодовые
измерения” мы упоминали, что снятие кодовой модуляции возможно, если в приемнике
производится копия такого же кода, которым модулируется спутниковый сигнал. Но и при
отсутствии копии (например, несущая L2 модулируется только Р-Кодом, которого может не
быть в приемнике) задача восстановления несущей решается достаточно просто. Для этого
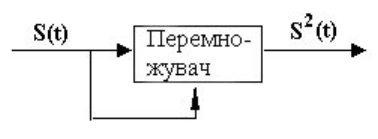
используют квадратування сигнала, который приходит от спутника. Идея образа объясняется на
рис.8.3. Кодированный сигнал от спутника разделяется на две части, которые поступают на два
входа перемножуючого устройства. На выходе образовывается сигнал, умноженный сам на себя,
то есть сведенный в квадрат.
Рис.8.3. К образу квадратування сигнала
Пусть сигнал, который проходит с несущей частотой f , имеет вид:
S(t)= А cos (2
f t +
м)
(8.10)
где - индекс “м” при начальной фазе
означает манипуляцию на 180
в
при изменению символов кода.
Используя известное соотношение cos
2
= (1/2)(1+cos2
), для исходного сигнала найдем:
6

S
2
(t)= A
2
cos
2
(2
f t +
м)
= (А
2/2
) + (А
2/2
)cos(2
2f t + 2
м)
. (8.11)
Умножение фазы
м
на 2 снимает фазовую манипуляцию, поскольку перебрасывание на 180
в
превращается в изменение на 360
об
, и на выходе получаем сигнал, который составляется из
постоянной составляющей (А
2/2
) и немодулированной несущей с амплитудой (А
2/2
) и удвоенной
частотой 2f, которую легко можно превратить в удобное для фазовых измерений значение.
Интегральный допплерівський счет. Под этим понимается счет периодов
допплерівського сдвига частоты
f
д
, возникающего через движение спутника, за некоторый
промежуток времени
t = t
2
- t
1
, где t
1
и t
2
- моменты начала и конца измерения. Например, можно
таким образом подсчитать приросты фазовых циклов при перемещении спутника по орбите с
одной точки в другую, а значит, определить и прирост расстояния от приемника. Это дает
возможность фиксировать положение спутника в разные эпохи (что напоминает метод третьих
различий при фазовых измерениях), или, другими словами, фиксировать последовательные
изменения расстояния от наземного приемника к спутнику. А это, в свою очередь, означает, что
могут быть определены соответствующие различия расстояний, которые позволяют вычислить
положение приемника гиперболической засечкой (см. раздел 6, подраздел «Геометрические
принципы позиционирования»).
Почему счет называется интегральным? В приемнике частота f
пр
,
что приходит
= f + f
д
смешивается с частотой fo опорного генератора,
как правило, кое-что отличной от частоты f излучаемых спутником
колебаний, и различие частот (fo
- f
пр
), которая называют частотой битья,
которое выделяется, интегрируется по времени на интервале (t
2
- t
1
).
Можно показать, что в результате интеграции определяется различие
расстояний от приемника до двух положений спутника, соответствующих
моментам t
1
и t
2
(рис.8.4). Фактически здесь происходит то же, что и при
интеграции допплерівського сдвига в лазерных интерферометрах при
перемещении отражателя, которое определяется как различие двух
положений отражателя в начальный и конечный моменты его движения
(см. раздел 5).
За допплерівським сдвигом можно найти и скорость изменения расстояния между
спутником и приемником (см. раздел 2).
Рис.8.4. К допплерівського подсчету фазовых циклов при движении спутника
ВОПРОС ДЛЯ САМОКОНТРОЛЯ
1. К чему относятся фазовые измерения?
2. Что является вымеренной величиной при фазовых измерениях?
3. Что является основной проблемой при фазовых измерениях?
4. В чем отличие фазовой псевдодальності от кодовой псевдодальності?
5. Что исключается во втором фазовом различии?
6. При решении которых уравнений получают окончательные значения различий
координат двух пунктов при фазовых измерениях?
7. Фазовые измерения выполняются на несущей частоте. Что необходимо для снятия
кодовой модуляции с целью восстановления несущей?
8. Что исключает первая, вторая, третья фазовые различия на начальной фазе?
9. Спутник движется по почти правильному кругу, в центре которого находится
приемник. При перемещении спутника с точки орбиты А в точку В расстояние к
7
