Лютц А.Ф., Сорокин В.П. Геодезические работы в путевом хозяйстве

Подождите немного. Документ загружается.

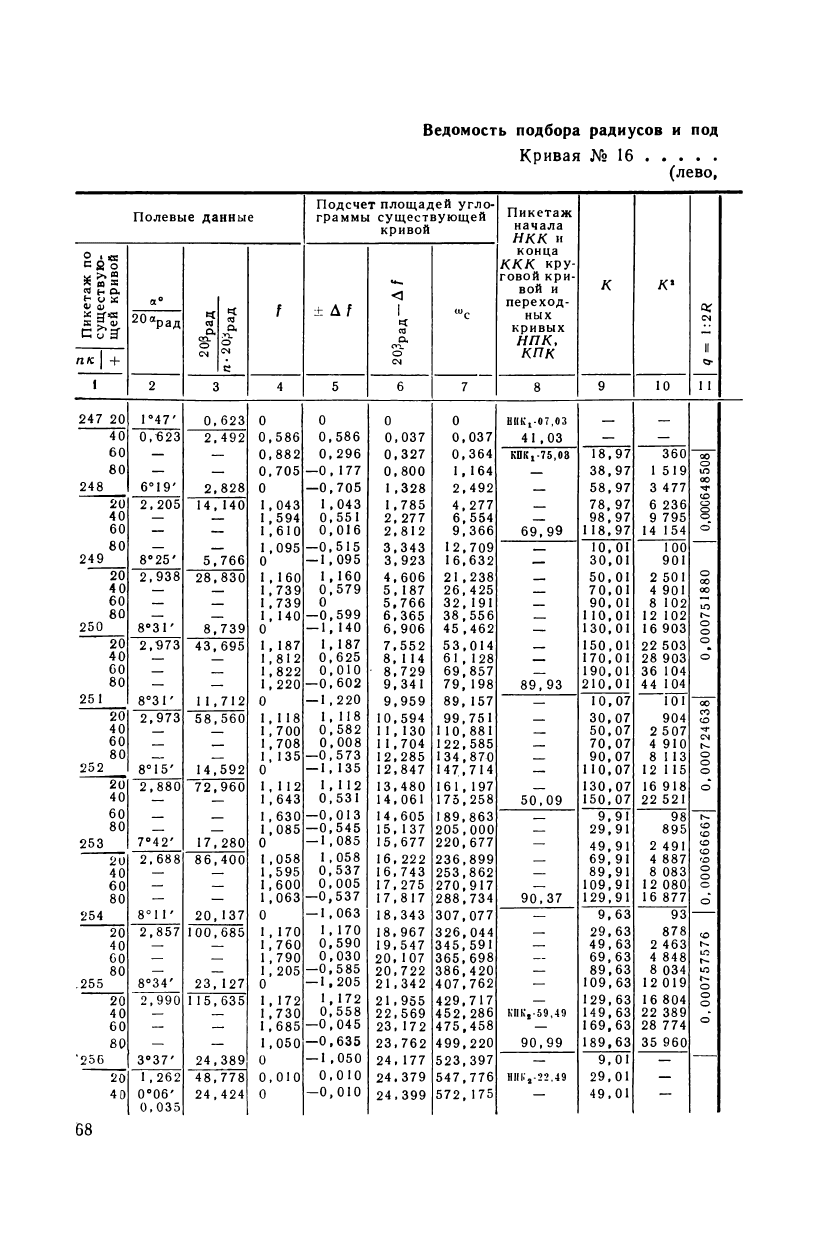
Ведомость подбора радиусов

и под

Кривая

№ 16

(лево,

Полевые данные

Подсчет площадей угло-

граммы существующей

кривой

Пикетаж

начала

НКК и

Cgo

f3 н о.

fr"

а°

-•п.

± A f

конца

ККК кру-

говой

кри-

вой и

переход-

20а

рад

о.

СП.

-•п.

± A f

с*

со

ных

кривых

НПК,

сч

О-

ПК | +

сч

<м

сч

кпк

сч

О-

4 5 6

247 20

1°47'

0, 623

HHKY07.03

0,^23

492

0,586

0,037

41 ,03

— —

—

0,882

0,296

0,327

0,364

КПК

-75,03

18,97

360

СЗО

80 —

0.705

—0, 177

0,800

1, 164

—

38,97

1 519

со

248 6°

2, 828

—0,705

,328

2,492

58,97

3 477

со

2, 205

14, 140

,043

1,594

1,610

,043

0,551

0,016

1,785

2,277

2,812

4, 277

6,554

9,366

69,99

78, 97

98,97

118,97

6 236

9 795

14 154

со

249

8°25'

766

,095

-0,515

-1,095

3,343

3,923

12,709

16,632

10,01

30,01

100

901

250

2,938

8°3 1'

28,830

8,739

, 160

1,739

.739

, 140

1,160

0,579

-0,599

— 1,140

4, 606

5, 187

5,766

6,365

6,906

21,238

26,425

32,191

38,556

45 ,462

50,01

70,01

90, 01

110,01

130,01

2 501

4 901

8 102

12 102

16 903

г^-

оооо

ооо

2,373

43,695

, 187

1,812

, 822

1,220

1, 187

0,625

0,010

—0,602

7,552

8,729

9,341

53,014

61,128

69,857

79,198

89, 93

150,01

170,01

190,01

210.01

22 503

28 903

36 104

44 104

8°ЗГ

11,712

— 1,220

9,959

89,157

—

10,07

101 оо

252

2,973

8°

58,560

14,592

1,118

,700

1,708

1, 135

1,118

0, 582

0, 008

—0,573

—

,135

10,594

1,130

11,704

12,285

12,847

99,751

10,881

122,585

134,870

147,714

30,07

50,07

70,07

90,07

110,07

904

2 507

4 910

12 115

со

"Г

сч

2,880

72,

960

1,112

1 ,

643

1,112

0,531

13,480

14,061

161,197

175,258

50,09

130,07

150,07

16 918

22 521

253

7°42'

17,280

1,630

,085

-0,013

-0,545

—

,085

14,605

15,137

15,677

189,863

205,000

220,677

9,91

29,91

49, 91

895

2 491

с£>

'•О

2. 688

86,400

,058

1,595

,600

,063

1,058

0,537

0, 005

—0,537

16,222

16,743

17,275

17,8 17

236,899

253,862

270,917

288,734

90, 37

69, 91

89,91

109,91

129,91

4 887

8 083

12 080

16 877

с£>

'•О

254

8°

20,137

— 1,063

18,343

307,077

—

9,63 93

,255

2,857

8°34'

100,685

23,127

, 170

1, 760

1,790

, 205

, 170

0,590

0,030

—0,585

— 1.205

18,967

19,547

20,107

20,722

21 ,342

326,044

345,591

365,698

386,420

407,762

29,63

49, 63

69,63

89,63

109,63

878

2 463

4 848

8 034

12 019

со

2, 990

115,635

, 172

,730

,685

1, 172

0,558

—0,045

21,955

22,569

23,172

429.717

452,286

475,458

h'llh',-59,49

129,63

149,63

169,63

16 804

22 389

28 774

—

,050

—0,635

23,762

499,220 90,99

189,63

35 960

'256

3°37'

24,389

— 1,050

24,177

523,397

—

9,01

—

1,262

48,778

0,010

24,379 547,776

1UI

Ь'

-22,49

29,01

—

0°06'

0,035

24,424

-0,010

24,399 572,175

—

49,01

—

68:

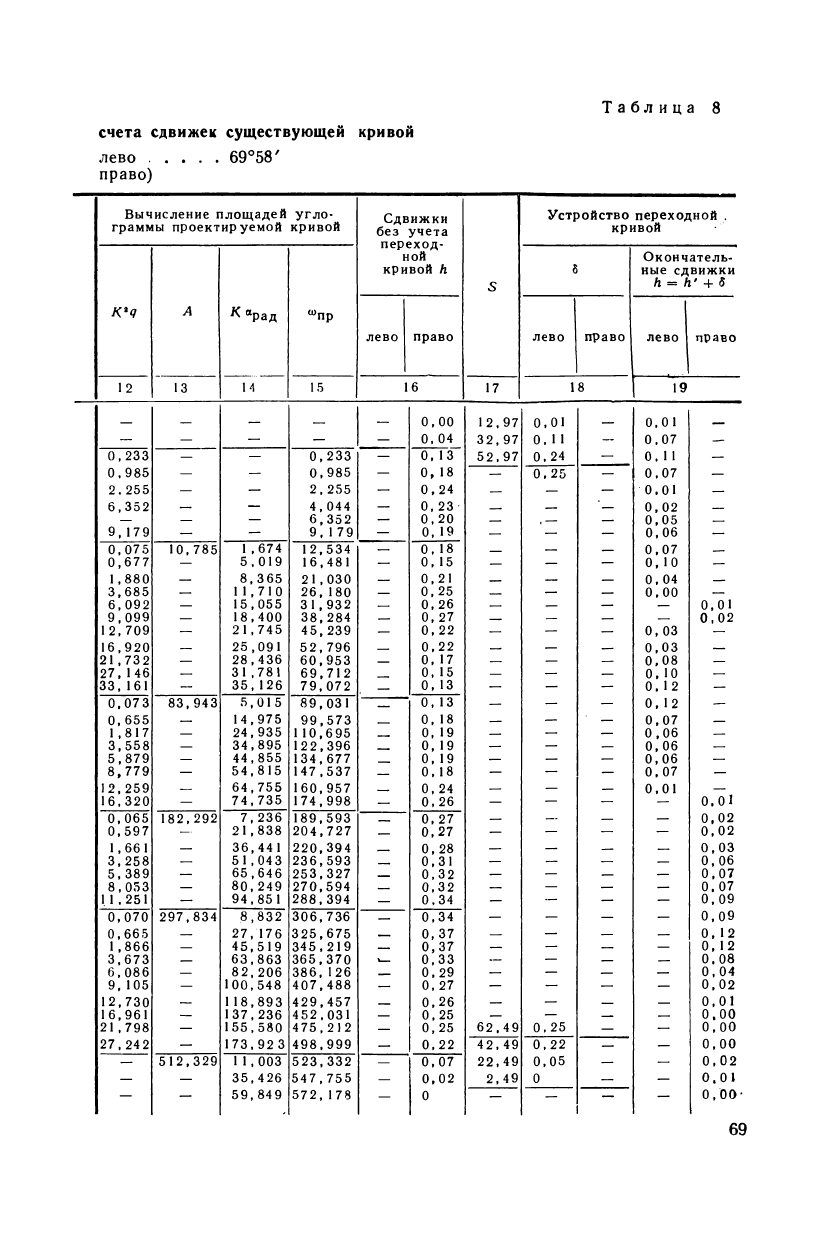
Таблица

счета сдвижек существующей кривой

лево 69°58'

право)

Вычисление площадей угло-

Слвижки

Устройство переходной

граммы проектируемой кривой

без

учета

кривой

ПРПруп ТТ.

исрслид

ной

Окончатель-

кривой

h Ь

ные

сдвижки

h = h' + 8

Ка

рад

пр

лево право

лево

право

лево

право

0,00

12,97

0,01 0.01

— — — — —

0,04

32,97

1 1

—

0.07

—

0,233

— —

0, 233

—

0, 13

52,97

0. 24

—

1 1

—

0,985

— —

0, 985

—

0, 18

—

0. 25

—

0.07

—

2.255

— —

2. 255

—

0, 24

— —

—

0.01

—

6,352

—

4,044

0,23

"—

0, 02

— — —

6,352

—

0,20

— , — —

0,05

—

9, 179

— —

—

0, 19

— — —

0,06

—

0,075

10,785

,674

12,534

—

0, 18

— —

0,07

0,677

—

5,019

16,481

—

0, 15

— — —

0, 10

—

,880

8,365

21 ,030

0,21

—

0,04

3,685

—

11,710

26, 180

—

0,25

— —

0,00

—

6,092

—

15,055

31,932

—

0, 26

— — — —

0,01

9,099

—

18,400 38,284

—

0,27

— —

0, 02

12,709

—

21 ,745

45,239

— 0, 22 —

—

0, 03

—

16,920

25,091 52,796

0,22

—

0,03

21 ,732

—

28,436

60,953

0, 17

— — —

0.08

—

27,146

—

31 .781

69,712

0, 15

— — —

0,10

—

33,161

—

35,126

79,072

0, 13

— — —

0.12

—

0.073 83,943

5,015

89,031

0, 13 —

—

0, 12

—

0, 655

14,975

99,573

0, 18

—

• —

0,07

—

,817

—

24,935

110,6 95

0, 19

— — —

0 ,06

—

3,558

—

34,895

122,396

0, 19

— — —

0,06

—

5,879

—

44,855

134,677

0, 19

— — —

0,06

—

8,779

—

54,815

147,537

0,18 — — —

0,07

—

12,259

64,755

160,957

0, 24

—

0,01

16,320

—

74,735

174,998

—

0, 26

—

— — —

0.01

0,065 182,292

7, 236

189,593

0, 27

— — — —

0,02

0,597

—

21 ,838

204,727

—

0,27

—

— — —

0,02

,661

36,441

220,394

0,28

0, 03

3, 258

—

51 ,043

236,593

0,31

— — — —

0, 06

5, 389

—

65,646

253,327

0,32

— — — —

0,07

8,053

—

80,249 270,594

0,32

— — — —

0.07

1 1

,251

—

94,85 1

288,394

—

0,34

—

0, 09

0,070

297,834 8,832 306,736

— 0,34

— — — —

0,09

0,665

27,176 325,675

0,37

—

0, 12

,866

—

45,519

345,219

0,37

— — — —

0, 12

3,673

—

63,863 365,370

0,33

— — — —

0.08

6, 086

—

82,206

386,126

0, 29

— — — —

0,04

9, 105

—

100,548

407,488

—

0, 27

— — —

—

0,02

12,730

18,893

429,457

0,26

—

0,01

16,961

—

137,236 452.031

—

0,25

— — —

0,00

21 ,798

—

155,580

475,212

—

0,25

62.49

0, 25

— —

0,00

27,242

—

173,92

498,999

—

0, 22

42, 49

0. 22

— —

0,00

—

512,329

11,003 523,332

—

0, 07

22,49

0,05

—

0,02

— —

35,426 547,755

—

0,02 2,49

0 — —

0.01

—

59,849

572,178

—

0,00-

69:

Подбор радиусов кривых при наличии крити-

ческих точек — один из сложных этапов работы по расчету кривых.

Сложность его состоит в том, что наряду с соблюдением основных

требований

при нанесении проектного положения угловой линии

на углограмму существующей кривой необходимо обеспечить на-

перед заданные величины сдвижек пути в критических точках и

максимально допустимую рихтовку вообще для всей кривой.

Последнее особенно важно потому, что в условиях эксплуатации

железных дорог очень редко встречаются кривые, содержащиеся

по одному радиусу. Чаще имеют место случаи, когда кривая имеет

несколько радиусов, иногда значительно отличающихся один от

другого. Причиной этому нередко служат неудовлетворительное

содержание кривых в плане, неправильная разбивка или общая де-

формация земляного полотна и сложные условия местности, выз-

вавшие устройство составных кривых.

Подбирая радиус кривой, проектировщик не может, конечно,

не учитывать указанных выше обстоятельств и назначает величину

сдвижки в соответствии с конкретными условиями пути (шириной

обочины земляного полотна, габаритом приближения строений

и т. д.).

К сожалению, этот очень важный, на наш взгляд, момент забы-

вают нередко инженеры-путейцы и в своих решениях становятся

При нанесении угловой линии должны соблюдаться следующие усло-

вия:

1) угол поворота существующей кривой должен оставаться без изме-

нения независимо от величины подбираемого радиуса;

2) кривая вновь подбираемого радиуса должна быть вписана в общий

угол поворота, образованный продолжением смежных прямых существую-

щего пути.

70:

подчас на неправильный путь, назначая несколько радиусов для

кривой даже и в том случае, когда в основе изменения радиуса су-

ществующей кривой лежит неудовлетворительное содержание ее

в плане.

Подбор радиусов кривых ведется обычно путем последователь-

ных приближений; для более простых случаев теперь внедряются

аналитические способы определения элементов существующих кри-

вых.

Ниже рассматриваются случаи подбора радиусов и подсчет

сдвижек для наиболее часто встречающихся кривых.

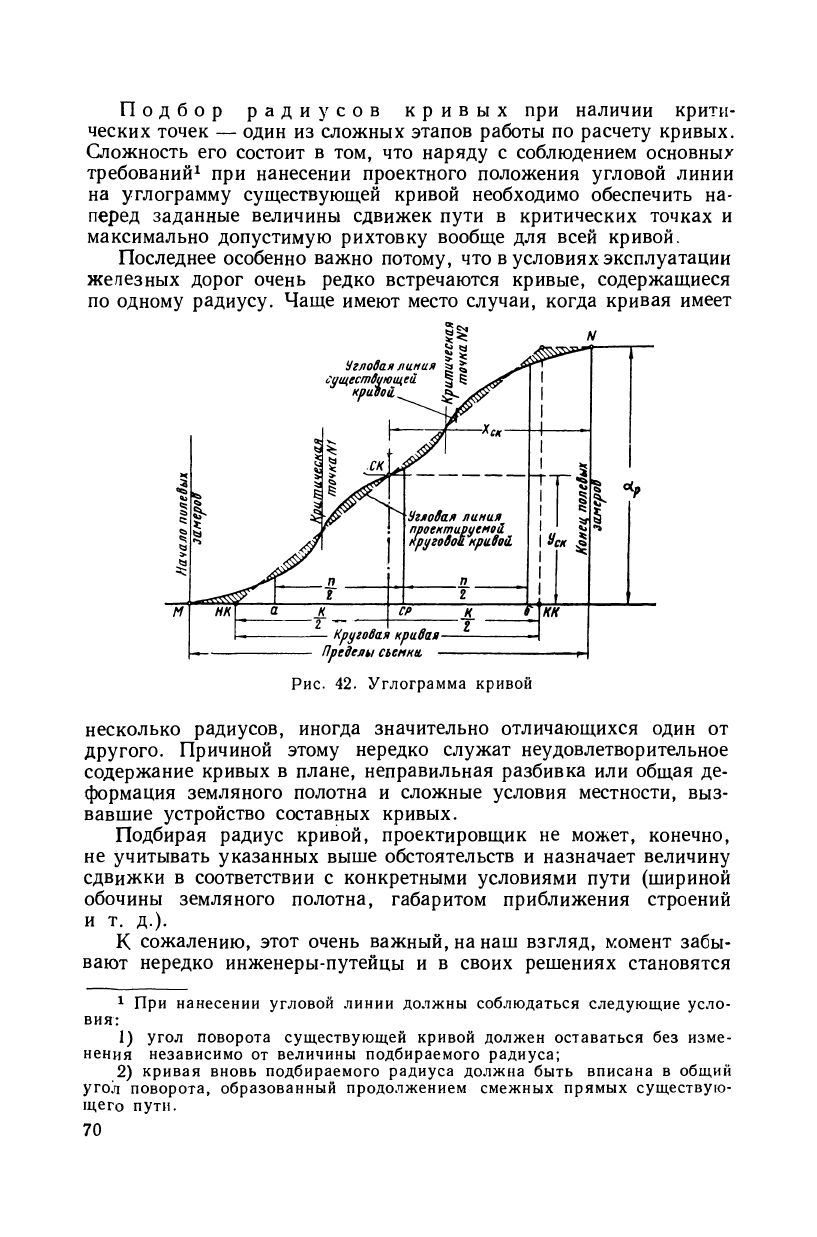
Случай 1. Кривая одного радиуса без переходных кривых,

углограмма которой представлена на рис. 42. Для нанесения на

этот график проектного положения угловой линии определяют сна-

чала положение точки СК (середины кривой), через которую про-

ходят все без исключения угловые линии правильных круговых

кривых, вписанных в данный угол. Для подсчета координат точки

СК пользуются формулами:

Хск = ^> (III.5)

ра л

Уск = > (HI.6)

где

o>,v

— площадь углограммы существующей кривой до точки N;

— У

гол

поворота всей кривой в радианах.

Положение точки СК по пикетажу можно получить, если из

пикетажного значения точки N вычесть величину — хек-

Проектную угловую линию проводят через точку СК так,

чтобы она возможно больше совпадала с угловой линией сущест-

вующей кривой. По длине кривой К, измеренной между точками

НК и К К с точностью до 1 м, определяют радиус по общеизвест-

ной формуле

= (III.7)

^рад

Если при этом значении К радиус окажется дробной величи-

ной, последнюю округляют до ближайшего целого. По округлен-

ному значению R сначала уточняют длину круговой кривой —

К = Ra

rai

\ прибавляя и вычитая из пикетажного значения точки

С К половину длины уточненной кривой, получают начало

НК и конец КК круговой кривой принятого радиуса.

Более точно и без построения углограммы радиус круговой

кривой можно определить по формуле, рекомендованной

инж. И. П. Маруничем

100^=

+ —

2u)

71:

где п — число «двадцаток» между точками а и б (см. рис. 42);

о)

— площадь углограммы существующей кривой до точки а;

— то же, до точки б;

со

ср

— то же, до средней точки между а и б.

По формуле (III. 8) определяют радиус круговой криЕой и при

наличии переходных кривых. Эта формула может быть использо-

вана также для определения радиусов ссставной кривой.

Точки а и б выбирают у концов переходных кривых и так, чтсбы

число делений п между ними было, как правило, четным.

Полученное по формуле значение радиуса округляют до целей

величины, по которой исчисляется полная длина круговой кривей.

Для подсчета сдвижек (рихтовок) кривой в критических точках

пути пользуются формулой

/1' = 0)

пр

-0)

, (И 1.9)

где о)

пр

—проектная площадь углограммы до рассматриваемого

сечения (точки);

оо

— площадь углограммы существующей кривой до того же

сечения (точки).

Из рис. 42 видно, что

пр ~2

Заменив а

рад

через получим

- JL

или ~ 2 ' R '

= ("МО)

где К — длина проектируемой круговой кривой от начала ее до

рассматриваемой точки;

q — коэффициент кривизны кривой, численно равный ^ .

Подставив значение <о

пр

из равенства (III. 10) в равенство (III.9),

получим величину сдвижки кривой в любой точке деления

в следующем виде:

h' =К

д —

оу

(III.11)

Пользуясь этой формулой, можно определить не только вели-

чину самой сдвижки, но и ее направление. Для определения на-

правления сдвижки кривой в любой точке пути пользуются сле-

дующими правилами:

если K

— (

- имеет знак +), сдвижка кривой

имеет одноименное направление с углом поворота кривой и на-

правлена внутрь кривой;

если К

д — (т. е. h' имеет знак —), сдвижка кривой

в данной точке разноименна с углом поворота и направлена

наружу кривой.

72:

Если при данном радиусе кривой сдвижка пути в критической

точке оказалась больше допустимой, проектирование угловой линии

и подсчет сдвижек пути в критических точках повторяют при дру-

гих значениях радиуса, добиваясь нужных величин сдвижек для

всех критических точек кривой.

Точки начала НК и конца КК круговой кривой окончательно

принятого радиуса выписывают в соответствующие по пикетажу

строки графы 8 «Ведомости подбора радиуса и подсчета рихтоЕок

су ществу ющей кривой».

Случай 2. Кривая одного радиуса с переходными кривыми

по концам. Проектирование угловой линии и подбор радиу-

са круговой кривой производятся в этом случае так же, как и

в первом.

Разница состоит здесь в том, что дополнительно к определению

точек НК и КК находят также точки начала НПК и конца КПК

переходных кривых. Для нахождения этих точек задаются обычно

длиной переходной кривой /, стандартные значения которой ука-

заны в табл. 9*.

Пользуясь принятыми значениями длины переходной кривой,

пикетажное положение точек НПК и КПК определяют по форму-

лам:

а) со стороны начала кривой

НПК = НК G-;

кпк = нк + -if; (ш.12)

б) со стороны конца кривой

НПК = КК + ^ ;

КПК = KK — Y'

где НК и КК — пикетажные значения точек начала и конца кру-

говой кривой;

—

длина переходной кривой.

Так как переходные кривые сдвигают круговую кривую внутрь,

величина рихтовки любой точки будет равна

h = h' ±8, (III.13)

где h' — сдвижка кривой в рассматриваемом сечении без учета

переходных кривых;

8 — сдвижка круговой кривой за счет переходных кривых.

* Табл. 9 длин переходных кривых взята из проекта Н и ТУ 1958 г.

Таблица 9

Длина переходных кривых в м

Радиус

Линии I категории Линии II категории

| Линии III категории

Радиус

Зон ы скоростей

кривой

ы скоростей

кривой

•

| 1

1 з

4 000

80— 60

40— 20 20 20

3 000

100— 80

60— 40

40— 20 40

20 0

2 500

120—100

80— 60

60— 40

40— 20

2 000 140—120

80 60— 40 80— 60

20 20

1 800

160—120

100— 80

60— 40

80— 60

60— 40

1 500

180—140 120—100

60 100— 80

60— 40

40— 20 40— 20

20 20

1 200 200—180

140—120

80— 60

120—100 80— 60

40 20

1 000

200-160

160—120

100— 80 160—120

80— 60

40 40

40—20

800

180—140

100— 80 180—140

100— 60

60—40

60— 40

700 160—140

160—140 120—100 160—140

120—100

60—40 80— 60

600

160—120 160—120 140—100

160—120

140—100

80— 60

60—40 20

500

140—120

140—120 160—120

160—120

80—60

100— 80 60—40

400

120—100 120—100

120—100

80—60

120—100

80—60

40—20

350

120—100

120—100 120—100

120—100

100—80

120—100

80—60

40—20

300 120— 80

120— 80

120—80

120—100

100—80

250

100— 80 100— 80

100— 80

100-80

100— 80

100—80 40

200

— —

—

100— 80

100—80

60—40

Примечания. 1. При двух значениях длин переходных кривых меньшие допускается применять толь-

ко в стесненных условиях.

2. На линиях I категории, на которых не предусматривается движение пассажирских поездов со скоро-

стями более 120 км/ч, допускается в трудных топографических условиях проектирозать переходные кривые по

нормам для линий II категории.

3. Деление участков пути на скоростные зоны должно производиться в зависимости от конфигурации про-

филя: 1-я зона — углубления профиля и примыкающие к ним участки затяжных спусков, а также прочие уча-

стки, проходимые грузовыми поездами хотя бы в одном из направлений с наибольшими или близкими к ним

скоростями; 3-я зона — возвышения профиля и примыкающие к ним участки затяжных подъемов, проходимые гру-

зовыми поездами в обоих направлениях со скоростями, близкими к расчетной скорости на руководящем уклоне;

2-я зона-г-участки, проходимые грузовыми поездами со средними скоростями.

Сдвижка круговой кривой в зависимости от длины переход*

ной кривой определяется по формуле

(III.14)

О —

24 R

где I — длина переходной кривой;

R — радиус круговой кривой.

В трудных условиях плана длина переходных кривых может

быть нестандартной и определяться по формуле

av*

(III.15)

где v — наибольшая скорость движения в км/ч в месте распо-

ложения данной кривой, которая принимается не более

4,24 j/7?;

а—коэффициент, принимаемый равным, как правило, 0,08

с уменьшением в трудных условиях до 0,05.

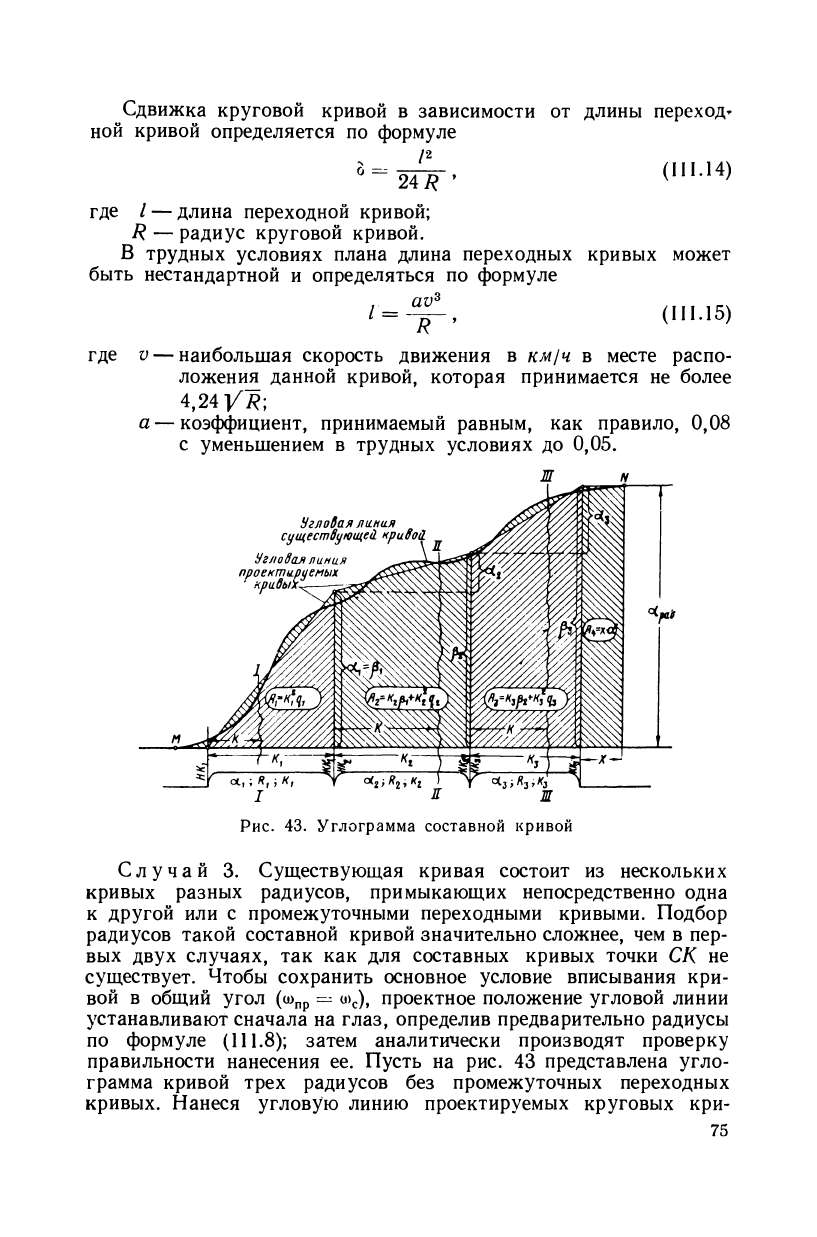
У глодая линия

существующей. А)

Угловая пиния

проектируемых

кривых

I Ж Ж

Рис. 43. Углограмма составной кривой

Случай 3. Существующая кривая состоит из нескольких

кривых разных радиусов, примыкающих непосредственно одна

к другой или с промежуточными переходными кривыми. Подбор

радиусов такой составной кривой значительно сложнее, чем в пер-

вых двух случаях, так как для составных кривых точки СК не

существует. Чтобы сохранить основное условие вписывания кри-

вой в общий угол (ш

пр

= и>

), проектное положение угловой линии

устанавливают сначала на глаз, определив предварительно радиусы

по формуле (111.8); затем аналитически производят проверку

правильности нанесения ее. Пусть на рис. 43 представлена угло-

грамма кривой трех радиусов без промежуточных переходных

кривых. Нанеся угловую линию проектируемых круговых кри-

75:

вых К и Кч, Кз, по масштабу графика определяют значение углов

поворота р

и З

каждой кривой относительно начальной

касательной. Пользуясь значениями углов

Рг и р

, определяют

углы поворота для каждой кривой в отдельности:

o-i = Рь )

«а =

Ра

—Рь (III.16)

аз =

Рз

— Р

. I

Контролем правильности определения этих углов служит об-

щий угол поворота существующей кривой, получаемый из изме-

рений, т. е.

&рад =

1 (рад) + <*2(рад) +

3(рад)

=*•

р3(рад). (III.17)

Убедившись в том, что равенство (III. 17) соблюдено, для каж-

дого из полученных значений углов поворота уточняют радиус или

длину круговой кривой, проверяя примыкание круговых кривых

впритык при данных значениях радиусов. Если условие выполнено,

то разница в кривизне стыкуемых кривых должна быть

J L<_L_

где R1 и R

— радиусы стыкуемых кривых.

По уточненному положению проектной угловой линии вычи-

сляют о)

пр

. Из рис. 43 видно, что

««пр = Л, + А

+ AS +

ХА

=24 + да. (II 1.18)

i=i

где

^ЧО + Р,);

Лз = -у- (Р. + ?.)•

Так как по условию вписывания ш

пр

= ш

, то

X =

(III.19)

рад

Если значение х, полученное расчетом, отличается от этой же

величины на углограмме не более чем на 1—2 м (1—2 мм на гра-

фике), условие вписывания кривой считают выполненным и пере-

ходят к расчету пикетажного положения точек НК и КК Для каж-

дого радиуса кривой в отдельности. Согласно рис. 43 пикетажточек

НКз = ККз —

/Сз,

где N — пикетажное положение точки конца полевых замеров;

х — расчетное значение расстояния между точками N

и ККз\

Кз — длина кривой (уточненная по формуле /Сз^а

Аналогично определяют пикетаж точек НК и КК и для двух

других кривых.

Для определения точек НПК и КПК задаются обычно дли-

ной I переходной кривой для какой-нибудь одной из концевых

круговых кривых, например Ki. Длину переходной кривой /

для второй концевой круговой кривой находят из условия со-

блюдения равенства

8i = 8

Согласно равенству (II 1.14) можно записать

,2 /2

/1 _ *2

24/?! "~24#

откуда

>,=/,]/£.

где U — принятая длина переходной кривой;

Ri — радиус концевой круговой кривой, для которой при-

нято значение 1\,

— то же, для которой определяется значение /

Если /

, полученная расчетом, резко отличается от длины су-

ществующей переходной кривой на углограмме, изменением соот-

/?2

ношения радиусов -=г- концевых кривых или длины переходной

А 1

кривой U добиваются необходимого значения /

и минимальных

сдвижек.

Дальнейшие расчеты по определению точек НПК и КПК, а

также сдвижек (рихтовок) кривой в критических точках аналогич-

ны расчетам, выполняемым для кривых одного радиуса с переход-

ными кривыми. Подсчет площадей проектируемых кривых ведется

в этом случае следующим образом. Пусть какая-нибудь критическая

точка пути находится в сечении I—I углограммы (рис. 43). Тогда

для интервала от точки HKi До точки KKi

= К

qi,

где К — длина круговой кривой от точки НК до рассматривае-

мого сечения;

qi — коэффициент кривизны первой кривой

77: