Лунин Л.С., Благин А.В., Баранник А.А. Лекции по физике. Часть I. Механика, молекулярная физика и термодинамика
Подождите немного. Документ загружается.


21
лезной массе m=20 тонн (т). Для сравнения: масса Метагалактики (дос-
тупной обнаружению современными методами радиоастрономии части
Вселенной) по приблизительным оценкам М
≈
10
53
кг.
ЛЕКЦИЯ 3. РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
1. Работа силы, мощность.
2. Механическая (кинетическая и потенциальная) энергия.
Закон сохранения механической энергии. Графическое
представление энергии. Коэффициент полезного действия (КПД).
3. Теория удара.
3.1. Работа силы, мощность
В качестве единой количественной меры различных форм движения
материи и соответствующих им взаимодействий в физике вводится ска-
лярная величина –
энергия.
В механике рассматривают механическую энергию (энергию ме-
ханического движения и механических взаимодействий). Для количе-
ственного описания обмена энергии между телами используют понятие
работа силы. Элементарной работой
δ
A силы F
r
на малом перемещении
r
d
r
точки О приложения силы называется скалярное произведение:
αδ
cos
(*)
FdsdtvFrdFA ===
→→→→
, (3.1)
где
r
– радиус-вектор точки О;
v
r
– ее скорость;
dt – малый промежуток времени, в течение которого сила
F
r
совер-
шает работу
δ
A;
α
– угол между направлением действия силы F
r
и направлением пе-
ремещения
r
d
r
(или v
r
).
Если угол
α
–острый, то
δ
A>0 и сила ускоряющая, если угол
α
–
тупой, то
δ
A<0 и сила тормозящая (трения, например). Переход (*) в
уравнение (3.1) справедлив в силу равенства
dsrddtt
=
⇒→
=
∆
r
0 . Из
уравнения (3.1) следует, что
сила не совершает работу, если точка при-
ложения силы
неподвижна (
0=rd
r
) и если сила направлена перпенди-
кулярно (по нормали) к траектории (
v
F
r
r
⊥
).

22
Таким образом, работа силы на участке траекторий от точки 1 до
точки 2 равна алгебраической сумме элементарных работ на отдельных,
бесконечно малых участках:
∫∫
==
→→
2
1
2
1
cos)( dssFdrFA
s
F
43421
α
. (3.2)
Геометрически работа – это площадь под кривой (рис. 3.1).
F
S
S
dS
δ
A
Рис. 3.1
Если
constF =
r
, то
∫
==
2
1
cos
α
FsdsFA
s
. Сила называется по-
тенциальной (консервативной), если ее работа зависит только от на-
чального и конечного положений тела и не зависит от формы ее тра-
ектории
. Для таких сил интеграл по замкнутому контуру L равен
0==
∫
→→
L
drFA . Для диссипативных сил работа зависит от формы тра-
ектории
при перемещении тела (сила трения).
Чтобы охарактеризовать скорость совершения работы, вводят поня-
тие мощности
dt
dA
N =
. За время dt сила F
r
совершает работу( rdF
A
r
r
=
δ
) и
мощность силы в данный момент (мгновенная мощность) равна
→→
→→
== vF
dt
rdF
N
. Единицы измерения: [A]=Дж; [N]=Ватт – Вт.
3.2. Механическая (кинетическая и потенциальная)
энергия. Закон сохранения механической энергии.
Графическое представление энергии. Коэффициент
полезного действия (КПД)
Кинетическая энергия
(КЭ) системы – это энергия механического
движения
этой системы. Сила F
r
, действующая на покоящееся тело и вы-
зывающая его движение, совершает работу; энергия движущегося тела
возрастает на величину затраченной работы. Таким образом, работа dA си-

23
лы на пути, который тело проходит от нулевой скорости до скорости v
r
,
идет на увеличение КЭ тела Т:
∫
==⇒==⋅===
→→→
v
mv
mvdvTmvdvdvvmdr
dt
vdm
rdFdTdA
0
2
2
r
r
r
. (3.3)
Кинетическая энергия Т является функцией состояния движе-
ния тела.
Поскольку скорость v
r
зависит от выбора СО, КЭ тела в раз-
личных
инерциальных системах отсчета (ИСО) имеет разные значения,
определяемые согласно теореме Кёнига: КЭ системы материальных то-
чек равна сумме КЭ всей массы системы, мысленно сосредоточенной в ее
центре масс и движущейся вместе с ним, и КЭ той же системы в ее относи-
тельном движении по отношению к поступательно движущейся системе
координат с началом в центре масс.
Потенциальная энергия (ПЭ) – это механическая энергия систе-
мы тел, определяемая их взаимным расположением и характером сил
взаимодействия между ними.
Телу присуща потенциальная энергия U, если оно находится в
поле потенциальных (консервативных) сил.
Работа консервативных сил
на элементарном перемещении равна приращению энергии U, взятому со
знаком «–», так как работа совершается за счет убыли потенциальной
энергии (зная U=f(r), можно определить модуль и направление силы F):
rdFdUdA
r
r
=
−
=
, (3.4)
тогда
∫
+−=
→→
constrdFU
, т.е. энергия U определяется с точностью до не-
которой произвольной постоянной, но это не влияет на физические
законы
, так как в них, обычно, входят или разность энергий, или их про-
изводные по координатам. Нулевой уровень ПЭ выбирается произвольно
из соображений удобства, поэтому может быть как больше, так и меньше
нуля. Согласно уравнению (3.4) для консервативных сил можно записать:
→→→
∇−=−=⇒
∂
∂
−=
∂
∂
−=
∂
∂
−= UgradUF
z
U
F
y
U
F
x
U
F
zyx
;;; , (3.5)
где
→→→→
∂
∂
+
∂
∂
+
∂
∂
= k
z
U
j
y
U
i
x
U
gradU
– градиент скаляра U, обозначается
→
∇U
(набла) и называется оператором Гамильтона или набла-оператором;
kji
r
r
r
,, – единичные векторы координатных осей (орты).
Конкретный вид функции U=f(r) зависит от характера силового
поля
. Так, тело, находящееся на высоте h<<R
Земли
от поверхности земли в
поле сил тяготения
, обладает потенциальной энергией:

24
,
1
)(
1
2
2
mghh
R
GM
m
RRh
GmM
dr
r
mM
Fdr
Земли
Земли
ЗемлиЗемли
Земли
h
Земли
R
Земли
R
h
Земли
R
Земли
R
Земли
консерв
тяготен
U
GAU
=≈=
−
+
−=
===−=∆
∫∫
+
+
(3.6)
где
консерв
тягот
А
- работа консервативных сил тяготения.
Энергия же сил тяготения отрицательна:
const
r
Mm
GrU +−=)(
. (3.6')
Подобно выражению (3.6) находится работа
переменной силы тяже-
сти при удалении ракеты на расстояние
h от центра Земли, сравнимое по ве-
личине с
R
Земли
, с учетом того, что сила и перемещение противонаправлены.
Аналогично, при упругих деформациях, деформирующая сила по
III закону Ньютона равна по величине упругой силе
kx. Элементарная ра-
бота:
dA=kxdx, а полная работа
⇒==
∫
x
kx
kxdxA
0
2
2
ПЭ упруго–
деформированного тела
2
2
kx
U =
. (3.7)
Потенциальная энергия системы является функцией ее состоя-
ния
. Она зависит только от взаимного расположения тел (конфигура-
ции) системы
и от ее положения по отношению к внешним телам.
Полная энергия тела складывается из его кинетической и потенци-
альной энергий:
E=T+U.
Рассмотрим систему материальных точек массами
m
1
,…,m
n
, движу-
щихся со скоростями
n
vv
r
r
,...,
1
. Обозначим равнодействующие внутренних
консервативных сил
n
FF
r
r
,...,
1
, а внешних консервативных сил –
→→
//
1
,...,
n
FF
;
внешние неконсервативные силы обозначим
→→
n
ff ,...,
1
.
При
v<<c массы тел не меняются и уравнения II закона Ньютона
имеют следующий вид:

25
++=
++=
→
→
→
→
→
→
→
→
.
................................
,
/
1
/
11
1
1
nnn
n
n
fFF
dt
dv
m
fFF
dt
dv
m
(3.8)
Двигаясь под действием сил, материальные точки за время dt пере-
мещаются на расстояние
→→
n
drdr ,...,
1
. Умножим уравнения (3.8) на соответ-
ствующие перемещения (для i-го случая):
→→→
→
→→
→
=+−
iiiiii
i
i
drfdrFFdr
d
t
dv
m )(
/
. (3.9)
Сложим уравнения (3.9) с учетом
→→
=
ii
vdtdr /
и (3.3), (3.4):
∑∑∑
→→→
→
→
→
→
=+−
i
ii
i
iii
i
iii
drfdrFFdvvm )(
/
или
неконс
dAdUdT
12
=+
. (3.10)
Переход системы из состояния 1 в состояние 2.
(3.10) – закон изме-
нения механической энергии.
Если внешние неконсервативные силы отсутствуют, то
E=T+U=const. (3.11)
Формула (3.11) – закон сохранения механической энергии: в системе
тел, на которые действуют только консервативные силы, полная меха-
ническая энергия сохраняется, то есть не изменяется со временем (нет ее
диссипации, т.е. рассеяния).
При этом может возникнуть вопрос: "А как же быть с внешними
консервативными силами?" Ответ: "Если внешние консервативные силы
нескомпенсированы, то в систему включают тела, воздействующие этими
силами, т.е. такие силы можно сделать «внутренними»".
Закон сохранения энергии является следствием фундаментального
свойства времени –
однородности. Однородность времени заключается в
том, что
физические законы инвариантны относительно выбора нача-
ла отсчета времени
.
Во многих случаях потенциальная энергия является функцией толь-
ко одной координаты
U=U(x). График зависимости U от какого-то одного
аргумента называется потенциальной кривой.

26
U
h
E
U
T
α
Рис. 3.2
Анализ потенциальных кривых позволяет определить характер
движения тела.
Особый случай представляют консервативные и замк-
нутые системы
, в которых
E=U+T=const.
Например, на рис. 3.2 приведено графическое представление
потенциальной энергии тела в поле сил тяготения, с учетом уравнения
(3.6) тангенс угла наклона зависит от массы тела:
tg
α
=mg.
Для ПЭ (рис. 3.3) сжатой пружины функция
U(x) имеет вид парабо-
лы В точках
± x
m
– ПЭ достигает максимума (КЭ Т=0). Система не может
выйти за пределы
± x
m
; говорят, что она находится в потенциальной яме.
В общем случае функция U(x) может иметь сложный график (см., на-
пример, рис. 3.4).
-x
m
x
m
+
E
U
x
0
Рис. 3.3
Частица, обладая энергией
E, как показано на рисунке, может нахо-
диться только в областях II и IV. Перейти из области II в область IV части-
ца не может: область III является
потенциальным барьером, для преодо-
ления которого частице надо сообщить дополнительную энергию (
U
1
-E). В
точке минимума производная
dU/dx=0, т. е. в этой точке находится по-
ложение равновесия
.

27
Коэффициентом полезного действия (КПД) называется отношение
полезной
(для какой-то практической цели) совершенной работы (энер-
гии) ко всей работе
, совершенной системой (к поступившей в систему
энергии):
соверш
полезн
соверш
полезн
Е
Е
А
A
==
η
. (3.12)
E
U
1
U
x
IIIII
I
V
I
Рис. 3. 4
3.3. Теория удара
Удар абсолютно упругих и неупругих тел
является ярким приме-
ром
выполнения законов сохранения импульса и энергии. Под ударом
(столкновением) в физике понимают
взаимодействие тел при их сближе-
нии
, которое длится очень короткое время, и условии, что на достаточно
большом расстоянии тела можно рассматривать как свободные.
В механике рассматривают удары, предполагающие контакт между
телами (удары бильярдных шаров, метеорита о землю, попадание пули в
тележку с песком).
Ударные F
удар
dp/dt=
∆
p/
∆
t (или мгновенные (
∆
t
∼
мкс))
силы взаимодействия между соударяющимися телами столь велики, что
внешними силами можно пренебречь и считать для таких систем законы
сохранения импульса и энергии выполненными. Тела во время удара ис-
пытывают деформации (упругие или неупругие). КЭ тел во время удара
преобразуется в ПЭ упругого соударения, а затем частично или полностью
вновь переходит в КЭ. Плоскость контакта называется
плоскостью удара,
а прямую, ей перпендикулярную и пересекающую ее в точке соприкосно-
вения, называют
линией удара. Если линия удара параллельна скоро-
стям
сталкивающихся тел, удар называется прямым; если эта линия
проходит через центры сталкивающихся тел, удар называют централь-
ным. Скорость тел не достигает своего прежнего значения после удара.
Отношение нормальных составляющих скорости после и до удара
называют
коэффициентом восстановления (скорости):
n
v
n
v
/
=
ε
. Если
ε
=0 – абсолютно неупругий удар (АНУ),
ε
=1 – абсолютно упругий удар

28
(АУУ). Для шаров из слоновой кости коэффициент
ε
=0,89, из стали –
ε
=0,56, а для свинцовых –
ε
=0,01 т.е. для реальных тел 0<
ε
<1.
Рассмотрим применение законов сохранения для прямого централь-
ного удара двух шаров.
ν
1
x
ν
2
Рис. 3.5
Абсолютно упругий удар (АУУ). Пусть
1
v
r
и
2
v
r
– скорости тел до, а
1
'v и
2
'v – после удара (рис. 3.5). В случае, если скорость
2
v
r
направлена
навстречу
1
v
r
, в формулах ниже учитывают, что проекция скорости
2
v
r
бу-
дет равна
2
v и все рассуждения остаются верными.
Для АУУ выполняются законы сохранения импульса
(так как
импульс – векторная величина, то записан в проекции на ось Ох) и
энергии
:
22112211
vmvmvmvm
′
+
′
=
+ . (3.13)
(
)
(
)
2
'
2
'
22
2
22
2
11
2
22
2
11
vmvmvmvm
+=+
, (3.14)
откуда
() ()
2211
2
2
2
22
2
1
2
11
222111
)'()'(
)()(
vvvv
vvmvvm
vvmvvm
+
′
=
′
+⇒
−=−
−
′
=
′
−
(3.15)
Выражая одну из скоростей ((3.13), (3.15))
2
1
21
2
1
2
112211
2
m
m
vv
m
m
m
vmvmvm
v −+=
′
−+
=
′
,
2112
'' vvvv
−
+
=
и приравни-
вая их
2
1
21
2
1
211
m
m
vv
m
m
vvv −+=−
′
+
, группируем
−+=
+
′
121
2
1
12
2
1
1
m
m
vv
m
m
v
,
откуда получаем
29
)(2
1
12
12
21122
2
1
2
1
12
1
mm
mmvvm
m
m
m
m
vv
v
+
−+
=
+
−+
=
′
,
.
)(2
21
12211
2
mm
mmvvm
v
+
−
+
=
′
(3.16)
При анализе упругих столкновений удобно один из шаров представ-
лять покоящимся (относительно шара
m
2
скорость
→→
→
−=
21
/
1
vvv ).
Рассмотрим
частный случай: АУУ – прямой центральный (лобо-
вой) удар при
ν
2
=0. Тогда из формулы (3.16)
)(
12
211
1
mm
mmv
v
+
−
=
′
и
21
11
2
2
mm
vm
v
+
=
′
получают:
а)
m
1
=m
2
, тогда
12
,0
1
vvv
=
′
=
′
(как бы «передача скорости»);
б)
m
1
>m
2
, тогда 0
2
,0
1
>
′
>
′
vv (оба мяча движутся в направлении ско-
рости первого мяча до удара);
в) m
1
<m
2
, тогда 0
2
,0
1
>
′
<
′
vv (первый мяч отскочит от второго);
г) m
1
<<m
2
, тогда 0
2
,
11
≈
′
≈
′
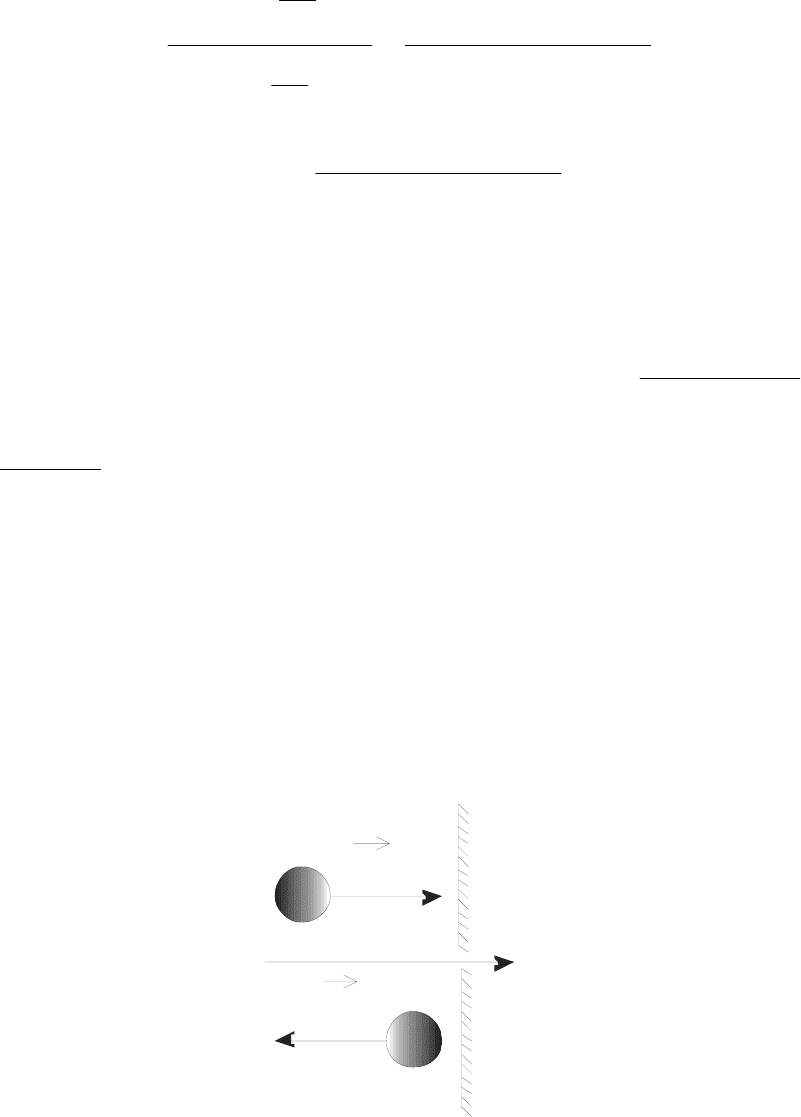
vvv (мячик отскочит от стены, см. рис.
3.6,
мячастеныстены
ppmvmp 2
111
=
⇒=− )
ν
1
x
ν
1
/
Рис. 3.6
Рассмотрим
частный случай: АУУ – непрямой нецентральный
удар
при
ν
2
=0 и m
1
<<m
2
(мяч ударяется о стенку, см. рис. 3.7). Для опре-
деления импульса, переданного стене, воспользуемся результатами пункта
г) решения предыдущего примера с учетом проекций импульса на ось Ох.
В данном случае:
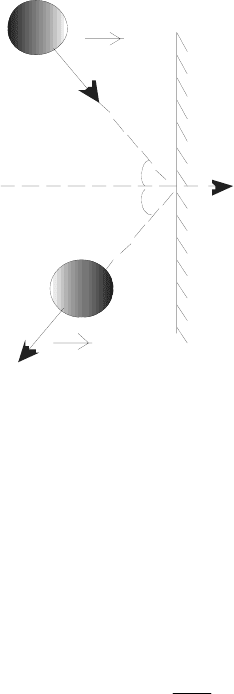
30
α
cos22
11)()(
vmрр
OxмячаOxстены
=
= .
Равенство углов падения и отражения в рассматриваемом случае
следует
из закона сохранения механической энергии при АУУ.
ν
1
x
ν
1
/
α
α
Рис. 3.7
В случае нецентрального удара частицы разлетаются под углом,
причем угол, на который изменяется направление скорости налетающей
частицы, называется углом рассеяния.
При m
1
=m
2
угол рассеяния – прямой, при m
1
<m
2
угол рассеяния лю-
бой (даже рассеяние назад), при m
1
>m
2
тяжелая частица не может откло-
ниться на угол, превышающий
1
2
arcsin
m
m
=
ϕ
.
Рассмотрим
частный случай: АУУ – прямой нецентральный удар
при
ν
2
=0 и m
1
=m
2
=m (шары в бильярде, см. рис. 3.7).
Из формул (3.13) и (3.14) имеем:
α
β
coscos
211
vvv
′
+
′
=
и
(
)
(
)
2
2
2
1
2
1
′
+
′
= vvv
(*), из треугольника скоростей (рис. 3.8) по теореме коси-
нусов:
(
)
(
)
[
]
)(180cos2
21
(*)
2
2
2
1
2
1
βα
+−
′′
+
′
+
′
=
o
4434421
vvvvv
,
откуда с учетом (*) ⇒
′′
21
2 vv
cos[180°-(
α
+
β
)]=0, ⇒ cos[180°-(
α
+
β
)]=0 и
α
+
β
=90°, т.е. при прямом нецентральном ударе бильярдные шары разле-
тятся
под прямым углом.
