Лухтура Ф.И. Таблицы газодинамических функций
Подождите немного. Документ загружается.

Ф. И. ЛУХТУРА
Т А Б Л И Ц Ы
ГАЗОДИНАМИЧЕСКИХ
ФУНКЦИЙ
(k = 1,3 ÷ 1,67)
СПРАВОЧНОЕ ПОСОБИЕ
МАРИУПОЛЬ, ПГТУ
2007
2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ПРИАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
КАФЕДРА ПРОМЫШЛЕННЫХ ТЕПЛОЭНЕРГЕТИЧЕСКИХ
УСТАНОВОК И ТЕПЛОСНАБЖЕНИЯ
Т А Б Л И Ц Ы
ГАЗОДИНАМИЧЕСКИХ ФУНКЦИЙ
СПРАВОЧНОЕ ПОСОБИЕ
Утверждено на методсовете
энергетического факультета
Протокол №____ от ___200__г.
МАРИУПОЛЬ, ПГТУ
2007
3
УДК 532.5. (075.8)
Таблицы газодинамических функций. Справочное пособие /
Сост.: Ф.И. Лухтура. – Мариуполь: ПГТУ, 2007. – 152 с.
Данное справочное пособие и методические указания адре-
сованы в первую очередь студентам инженерных специально-
стей 7.090510 – Теплоэнергетика, 7.090406 – Промышленная
теплотехника, 7.092501 – Автоматизация управления техноло-
гическими процессами, 7.092301 – Технология сварочного обо-
рудования и др., изучающих курс или элементы газовой дина-
мики, для ознакомления с устройством газодинамических таб-
лиц и правилами пользования ими. Справочное пособие может
быть использовано студентами старших курсов при выполнении
курсовых и дипломных работ. Полезно также для работников
научно-исследовательских институтов и конструкторских бюро,
занимающихся газодинамическими расчетами и исследования-
ми.
Справочное пособие содержит таблицы величин основных
ГДФ для значений показателя изоэнтропы k = 1,3÷1,67, для ве-
личин приведенной скорости
1
1
010
−
+
÷=
k
k
,λ .
Приводятся формулы, иллюстрирующие применение таб-
лиц ГДФ в расчетах параметров потока при течении в трубах и
каналах, в элементах проточной частей лопаточных машин, ра-
ботающих на различных газах и газовых смесях.
Справочное пособие может быть использовано при расче-
тах и исследованиях энергетических лопаточных машин и аппа-
ратов, а также в различных областях дозвуковой, околозвуковой
и сверхзвуковой аэродинамики.
Составитель Ф.И.Лухтура, ст. преп.
Отв. за выпуск В.Н.Евченко, доц., к.т.н
Рецензент В.А.Маслов, проф., д.т.н.

4
стр.
5
8
10
13
17
21
27
28
30
33
47
60
71
97
123
150
151
СОДЕРЖАНИЕ
Введение _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Условные обозначения _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1 Краткий обзор содержащихся таблиц. Описание функций и
их основные свойства _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1.1 Газодинамические функции
(
)
λ
τ
,
(
)
λ
π
,
(
)
λ
ε
, харак-
теризующие термодинамическое состояние газа _ _ _ _ _ _ _
1.2 Функции
(
)
λ
q и
(
)
λ
y , характеризующие поток массы
1.3 Функции z(λ), характеризующая импульс потока, ϕ(λ)
и χ(λ), характеризующие соответственно адиабатное и изо-
термическое течение с трением _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 2 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 3 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 4 (для k = 1,3) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 5 (для k = 1,4) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 6 (для k = 1,67) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 7 (для k = 1,3) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 8 (для k = 1,4) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 9 (для k = 1,67) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Таблица 10 – Постоянные коэффициенты газодинамических
функций _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Перечень ссылок_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
5
ВВЕДЕНИЕ
Газодинамические расчеты и исследования энергетических
машин, расчеты аэродинамических труб, сопел, эжекторов, те-
чения газовых потоков в трубах и каналах, расчеты обтекания
тел газовыми до- и сверхзвуковыми потоками основаны на гро-
моздких и сложных уравнениях газовой динамики.
При широком распространении в современной технике
энергетических машин и аппаратов снижение трудоемкости
расчетов приобретает весьма существенное значение.
Уже продолжительное время в газодинамических расчетах
и при обработке экспериментальных данных применяются без-
размерные газодинамические функции, характеризующие со-
стояние потока в различных его сечениях. Использование этих
функций приводит к уменьшению объема расчетных работ и
облегчает труд расчетчика-газодинамика. Стремление облегчить
труд отразилось в создании большого числа газодинамических
таблиц и диаграмм. Применение таблиц особенно полезно в
прикидочных расчетах.
Затабулированные зависимости, полученные из уравнений
одномерного течения, позволяют обходиться без ряда аналити-
ческих вычислений. При дополнительных условиях они могут
применяться и в расчетах пространственных течений.
Таблицы составляются применительно к тем или иным мо-
делям газа, используемых в газовой динамике и отражающие
различные приближения к реальным свойствам газов.
Аналитические выражения рассматриваемых функций по-
лучены при допущении, что газ является совершенным (идеаль-
ным), т.е. показатель изоэнтропы не зависит от температуры и
давления. Для несовершенных (реальных) газов зависимость
показателя изоэнтропы от температуры и давления может быть
учтена выбором функций при соответствующих значениях k.
Отличительными чертами модели совершенного газа явля-
ются постоянство состава газа (или смеси газов), постоянство
теплоемкости, применение термического уравнения состояния
(уравнение Менделеева-Клапейрона) в форме
RTp
=
ρ
(1)
и калорического уравнения состояния в форме
6
1
−
=
k
kRT
i . (2)
При использовании модели совершенного газа с перемен-
ной теплоемкостью, т.е. отказавшись от предположения о по-
стоянстве теплоемкости, калорическое уравнение состояния (2)
в этом случае представляет собой более сложную функцию i (T).
При высоких температурах многоатомные газы диссоции-
руют и в модели диссоциирующего газа не только теплоемкость,
но и молекулярная масса зависит от состояния газа. Термиче-
ское уравнение состояния применяют в виде
T
R
p ρ
µ
=
, где мо-
лекулярная масса зависит от степени диссоциации газа. Обычно
в модели такого газа учитываются и последствия ионизации газа
при высокой температуре.
Если имеется необходимость учесть собственный объем
молекул газа и взаимодействие между молекулами до их соуда-
рения (сильно сжатый газ), то уравнение состояния применяется
в более сложных формах, чем (1), и мы приходим к модели ре-
ального газа.
Модель диссоциирующего газа отражена в изданиях [1-3].
Специальные таблицы для расчета обтекания затупленных тел в
рамках той же модели приводятся в [4-6].
Таблицы и диаграммы для течения совершенного газа как
изоэнтропных, так и с прямыми скачками уплотнения для k = 1,4
даны в упомянутом атласе [1].
Подробные таблицы для расчета изоэнтропных одномерных
течений в рамках модели совершенного газа с учетом зависимо-
сти теплоемкости от температуры имеются в [7]. Они построены
для показателей изоэнтропы от 1,01 до 1,41 через 0,01 и с шагом
по М = w/a равным 0,01.
Для этой же модели с постоянными показателями изоэн-
тропы от 1,05 до 1,7 через 0,05 даны газодинамические функции
в [8]. Здесь в качестве аргумента принята безразмерная скорость
λ = w/w
∗
= w/а
∗
.
Физическим и термодинамическим свойствам воздуха и
других газов посвящены таблицы [9,10].
Кроме указанных специальных изданий с той или иной
полнотой, таблицы ГДФ приводятся почти во всех учебниках

7
[11,12] и задачниках [13,14] по газовой динамике. Однако в пе-
речне приведенных таблиц и обозначениях в различных учеб-
ных изданиях имеются большие различия. При этом интервал
изменения и выбор независимых аргументов не всегда достато-
чен для проведения более точных вычислений. Кроме того,
обычно библиотеки не располагают необходимым количеством
экземпляров учебников, достаточным для использования газо-
динамических таблиц при изучении студентом газовой динами-
ки. Предназначение настоящего издания – частично восполнить
этот пробел.
При составлении таблиц за независимые переменные (в ка-
честве аргумента) выбраны приведенная скорость λ и число Ма-
ха М. Интервал изменения ∆λ и ∆М равен 0,01. Величины функ-
ций внутри интервала могут быть найдены линейной интерпо-
ляцией. Значения λ ограничены величиной
1
1
−
+
=
k
k
max
λ .
Значения функций вычислялись на ПЭВМ и приведены в
таблицах с точностью до пятого знака, как правило, удовлетво-
ряющей при расчетах. По сравнению с ранее изданными, табли-
цы ГДФ включают практически только основные газодинамиче-
ские функции, часто и в основном используемые для расчетов
параметров течения в каналах, соплах, струях в различных теп-
лотехнических и энергетических установках.
Вычислительные работы производились на ПЭВМ кафедры
ПТЭУ и ТС. В расчетах на вычислительной машине принимали
участие студенты гр. ПТЭ-03 ПГТУ А. Грицаенко и А. Грицен-
ко. Большая помощь в обработке цифрового и графического ма-
териала была оказана студентом гр. ПТЭ-04 ПГТУ О. Шепеле-
вым и сотрудником кафедры ТТМП Е. Л. Воробьевой. Автор
выражает им глубокую благодарность.
8
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
k – показатель изоэнтропы (адиабаты)
С
р
– удельная теплоемкость при постоянном давлении, Дж/кг⋅К
С
v
– удельная теплоемкость при постоянном объеме, Дж/кг⋅К
R
µ
– универсальная газовая постоянная, равная 8314 Дж/кмоль⋅К
µ
µ
R
R = – газовая постоянная (удельная), Дж/кг⋅К
µ - молекулярная масса газа (смеси газов)
F – площадь живого сечения потока, м
2
w – скорость газа, м/с
а – скорость звука в потоке газе, м/с
m – массовый расход, кг/с
р – давление, н/м
2
Т – термодинамическая температура, К
ρ - плотность, кг/м
3
i – энтальпия, Дж/кг
I – полный импульс газового потока (импульс в пустоте), н
∗∗
==
a
w
w
w
λ - приведенная скорость (коэффициент скорости)
a
w
M = - число Маха
max
w
w
=Λ - безразмерная скорость
()
0
T
T
=λτ - функция приведенной температуры
()
0
p
p
=λπ - функция приведенного давления
()
0
ρ
ρ
λε = - функция приведенной плотности
()
F
F
w
w
q
∗
∗∗
==
ρ
ρ
λ - функция приведенного расхода (приведенной
плотности тока (потока), плотности потока массы)
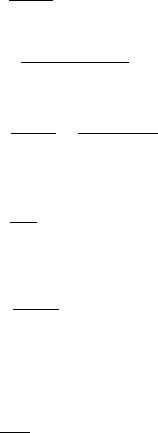
9
()
(
)
()
λπ
λ
λ
q
y = - функция статического импульса газового потока
()
∗∗∗
+
+
=
Fpmw
pFmw
z 2λ - функция приведенного полного импульса
()
0
2
0
p
wp
Fp
J
f
ρ
λ
+
== - функция приведенной плотности пото-
ка импульса
()
2
2
1
λ
λ
λϕ ln+= - функция, используемая при адиабатном тече-
нии газа в цилиндрических трубах
()
2
2
1
Mln
kM
+=λχ - функция, используемая при изотермиче-
ском течении газа в цилиндрических трубах
тр
λ
- коэффициент трения (коэффициент Дарси)
a
p
p
0
0
=Π - располагаемый (полный) перепад давления.
И н д е к с ы:
0 – величины, характеризующие параметры изоэнтропно затор-
моженного потока (полные параметры или параметры торможе-
ния)
∗ - параметры в критическом сечении (критические параметры)
а – параметры во внешней среде
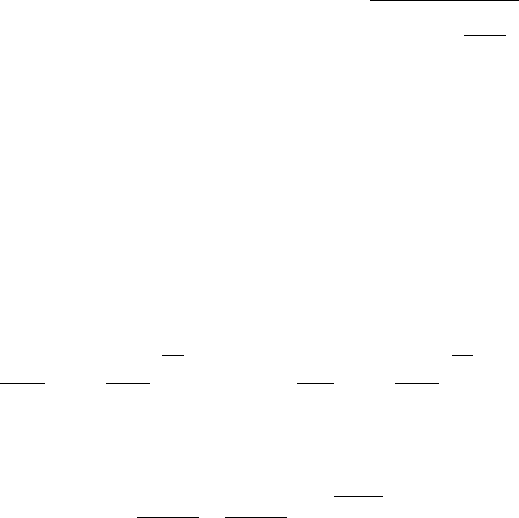
10
1 КРАТКИЙ ОБЗОР СОДЕРЖАЩИХСЯ ТАБЛИЦ.
ОПИСАНИЕ ФУНКЦИЙ И ИХ ОСНОВНЫЕ СВОЙСТВА
Таблицы 1 и 2 носят справочный характер и, вероятно, не
требуют пояснений.
Таблица 3 представляет стандартную атмосферу, к которой
приводятся некоторые газодинамические расчеты для удобства
сравнения. Отсутствие определенности в состоянии атмосферы
у Земли и в изменении ее состояния с увеличением высоты соз-
дает серьезные затруднения для технических расчетов. Необхо-
димость унификации расчетов привела к созданию условной
стандартной атмосферы (СА). СА является единым законом
изменения давления, температуры и плотности воздуха по высо-
те h, отсчитываемой от среднего уровня моря (h = 0 м).
Для тропосферы температура и плотность связаны с гео-
метрической высотой следующими зависимостями
hTT
⋅
−
=
β
ст0
;
⋅
−
=
ст0
ст0
1
T
h
RT
p
β
ρ ,
где β = 0,0065
0
С/м – градиент температуры по высоте;
Т
0ст
, ρ
0ст
= р
0ст
/(RТ
0ст
), р
0ст
– соответственно термодина-
мическая температура Кельвина, плотность воздуха и давление
на высоте h = 0 м (Т
0ст
= 288 К, р
0ст
= 760 мм рт. ст.);
R – газовая постоянная для воздуха (R = 287,14 Дж/(кг⋅К)).
Формулы для расчета давления (барометрическая формула)
и плотности атмосферы с линейным распределением температур
согласно основному уравнению гидростатики (при допущении,
что ускорение свободного падения по высоте тропосферы не
изменяется и принимается равным g = 9,81 м/с
2
= const)
R
g
T
h
p
p
β
β
⋅
−=
ст0ст0
1
;
1
ст0с0
1
−
⋅
−=
R
g
T
h
β
β
ρ
ρ
Для участков атмосферы с Т = const (стратосфера) расчет-
ные формулы будут
страт0
страт0страт0
RT
gh
страт
e
p
p
−
==
ρ
ρ
