Лотов В.И. Теория вероятностей. Конспект лекций
Подождите немного. Документ загружается.


¯
¯
¯
¯
N
Z
−M
g
ε
(y)dF (y) −
N
Z
−M
g(y)dF (y)
¯
¯
¯
¯
≤
ε
2
.
Следовательно, для достаточно больших n интегралы
∞
R
−∞
g(y)dF
n
(y) и
∞
R
−∞
g(y)dF (y)
отличаются от
N
R
−M
g
ε
(y)dF
n
(y) и
N
R
−M
g
ε
(y)dF (y) соответственно менее, чем на ε. Но
N
Z
−M
g
ε
(y)dF
n
(y) =
k−1
X
i=0
g(y
i
)[F
n
(y
i+1
) −F
n
(y
i
)] →
k−1
X
i=0
g(y
i
)[F (y
i+1
) −F (y
i
)]
=
N
Z
−M
g
ε
(y)dF (y).
Поэтому
lim sup
n→∞
∞
Z
−∞
g(y)dF
n
(y) ≤ ε + lim sup
n→∞
N
Z
−M
g
ε
(y)dF
n
(y) = ε +
N
Z
−M
g
ε
(y)dF (y)
≤ 2ε +
∞
Z
−∞
g(y)dF (y),
и аналогичное неравенство верно для нижнего предела. Теорема доказана.
Замечания
1. Если F непрерывна, то слабая сходимость F
n
⇒ F эквивалентна сходимости
F
n
(y) → F (y) равномерно по всем y, т. е. sup
y
|F
n
(y) − F (y)| → 0.
Доказательство. Пусть точки y
0
= −∞, y
1
, . . . , y
k
= ∞ таковы, что
F ( y
i
) −F (y
i−1
) ≤ ε/2.
Тогда найдется n
0
такое, что при n ≥ n
0
|F
n
(y
i
) −F (y
i
)| ≤ ε/2 для всех i = 0, . . . , k.
Заметим при этом, что F
n
(±∞) = F (±∞). Пусть теперь y произвольно. Для него
найдется число i такое, что y ∈ [y
i−1
, y
i
). Тогда
F
n
(y) − F (y) ≤ F
n
(y
i
) −F (y
i−1
) ≤ F (y
i
) +
ε
2
− F(y
i−1
) ≤ ε,
F
n
(y) − F (y) ≥ F
n
(y
i−1
) −F (y
i
) ≥ F (y
i−1
) −
ε
2
− F(y
i
) ≥ −ε,
откуда следует наше утверждение.
2. Если F
n
и F дискретны и имеют скачки в одних и тех же точках y
1
, y
2
, . . ., то
слабая сходимость F
n
⇒ F эквивалентна сходимости F
n
(y
i
+0) −F
n
(y
i
) → F (y
i
+0) −
F (y
i
).
3. Слабая сходимость F
n
⇒ F ровным счетом ничего не говорит о сходимости
случайных величин X
n
⊂= F
n
, они вообще могут быть заданы на разных вероятност-
ных пространствах. Даже если они заданы на одном пространстве, то следующий
81

пример показывает, что ни о какой сходимости случайных величин не может быть
речи.
Пусть при однократном бросании монеты X
1
равно числу выпавших гербов (X
1
принимает только значения 1 и 0 с равными вероятностями), а X
2
равно числу выпав-
ших решек. Ясно, что последовательность X
1
, X
2
, X
1
, X
2
, . . . ни к чему не сходится,
хотя все члены этой последовательности имеют одно и то же распределение.
В качестве примера слабо сходящейся последовательности функций распределе-
ния можно рассмотреть F
n
(y) = U
−
1
n
,0
(y). Здесь F
n
(y) → I
0
(y) для всех y, кроме
точки разрыва y = 0.
Теорема. Если X
n
P
→ X, то F
X
n
⇒ F
X
. Обратное неверно. Однако если F
X
= I
a
— вырожденное распределение, то из F
X
n
⇒ F
a
следует X
n
P
→ a.
Доказательство. Пусть g — непрерывная ограниченная функция, тогда
g(X
n
)
P
→ g(X), и в силу теоремы о мажорируемой сходимости Eg(X
n
) → Eg(X), что
доказывает первую часть теоремы. Далее, если F
X
n
⇒ F, то
P(|X
n
− a| < ε) = P(a −ε < X
n
< a + ε) ≥ P(a −
ε
2
≤ X
n
< a + ε) =
= F
X
n
(a + ε) −F
X
n
(a −
ε
2
) → 1,
поскольку a + ε и a −
ε
2
являются точками непрерывности функции распределения
F
a
. Теорема доказана.
Таким образом, закон больших чисел также является одним из примеров слабой
сходимости распределений F
S
n
/n
⇒ F
a
.
4.4. Характеристические функции
Наряду с вещественнозначными случайными величинами можно рассматривать
и комплекснозначные вида X
1
+ iX
2
. По определению полагаем
E(X
1
+ iX
2
) = EX
1
+ iEX
2
.
Независимость случайных величин X
1
+iX
2
и Y
1
+iY
2
можно понимать как независи-
мость σ-алгебр σ(X
1
, X
2
) и σ(Y
1
, Y
2
), порожденных случайными векторами (X
1
, X
2
)
и (Y
1
, Y
2
). Нетрудно проверить также для комплекснозначных случайных величин
выполнение всех основных свойств математических ожиданий (кроме, разумеется,
тех, где сравниваются величины без модуля), включая свойство E (XY ) = EXEY
для независимых случайных величин.
Определение. Характеристической функцией (х. ф.) случайной величины X
называется
ϕ
X
(t) = Ee
itX
=
∞
Z
−∞
e
ity
dF
X
(y) =
∞
Z
−∞
cos ty dF
X
(y) + i
∞
Z
−∞
sin ty dF
X
(y), −∞ < t < ∞.
Если F
X
абсолютно непрерывна, то х. ф. есть преобразование Фурье плотности
распределения. В соответствии с правилом вычисления математических ожиданий
функций от случайных величин, имеем
ϕ
X
(t) =
∞
P
k=1
e
ity
k
P(X = y
k
) (для дискретных распределений),
∞
R
−∞
e
ity
f
X
(y)dy (для распределений с плотностью).
82

Х.ф. всегда существует, так как
|ϕ
X
(t)| =
¯
¯
¯
¯
¯
¯
∞
Z
−∞
e
ity
dF
X
(y)
¯
¯
¯
¯
¯
¯
≤
∞
Z
−∞
¯
¯
e
ity
¯
¯
dF
X
(y) = 1.
Свойства характеристических функций.
1. ϕ
X
(0) = 1, |ϕ
X
(t)| ≤ 1.
2. ϕ
aX+b
(t) = e
itb
ϕ
X
(at), ϕ
X
(t) = ϕ
X
(−t) = ϕ
−X
(t).
3. Если случайные величины X
1
, . . . , X
n
независимы, то
ϕ
X
1
+...+X
n
(t) = ϕ
X
1
(t) . . . ϕ
X
n
(t).
4. Если существует E|X|
k
< ∞, k ≥ 1, то существует непрерывная k-я производ-
ная ϕ
(k)
X
(t) и ϕ
(k)
X
(0) = i
k
EX
k
.
Доказательство. В силу того, что равномерно по t выполняется
¯
¯
¯
¯
¯
¯
∞
Z
−∞
iye
ity
dF
X
(y)
¯
¯
¯
¯
¯
¯
≤
∞
Z
−∞
|y|dF
X
(y) < ∞,
можно дифференцировать под знаком интеграла:
ϕ
0
X
(t) =
∞
Z
−∞
e
ity
dF
X
(y)
0
=
∞
Z
−∞
iye
ity
dF
X
(y).
Дальше действуем по индукции. Пусть при l < k
ϕ
(l)
X
(t) =
∞
Z
−∞
(iy)
l
e
ity
dF
X
(y),
тогда
ϕ
(l+1)
X
(t) =
∞
Z
−∞
(iy)
l+1
e
ity
dF
X
(y)
в силу равномерной по t сходимости интеграла в правой части. Итак,
ϕ
(k)
X
(t) =
∞
Z
−∞
(iy)
k
e
ity
dF
X
(y),
и остается положить t = 0 в этом выражении.
Установим непрерывность производной.
|ϕ
(k)
X
(t + h) −ϕ
(k)
X
(t)| =
¯
¯
¯
¯
i
k
∞
Z
−∞
y
k
¡
e
i(t+h)y
− e
ity
¢
dF
X
(y)
¯
¯
¯
¯
≤
∞
Z
−∞
|y|
k
¯
¯
e
ihy
− 1
¯
¯
dF
X
(y) → 0
83
в силу теоремы о мажорируемой сходимости, т. к. e
iXh
− 1 → 0 при h → 0, и, кроме
того,
|X|
k
¯
¯
e
ihX
− 1
¯
¯
≤ 2|X|
k
, E|X|
k
< ∞.
Случай k = 0 не исключается, т. е. мы установили кроме всего прочего, что х. ф.
является равномерно непрерывной функцией.
5. Если E|X|
k
< ∞, то в окрестности точки t = 0
ϕ
X
(t) = 1 +
k
X
j=1
(it)
j
j!
EX
j
+ o(|t|
k
).
Примеры.
1. Если X ⊂= I
a
, то ϕ
a
(t) = e
iat
.
2. Если X ⊂= Π
λ
, то
ϕ
X
(t) =
∞
X
k=0
e
itk
λ
k
k!
e
−λ
= exp{λ(e
it
− 1)}.
3. Пусть X ⊂= Φ
α,σ
2
. Воспользуемся тем, что X = σY + α, где Y ⊂= Φ
0,1
. Значит,
ϕ
X
(t) = e
iαt
ϕ
Y
(σt). Найдем ϕ
Y
(t). Продифференцировав эту функцию по t, получим
ϕ
0
Y
(t) =
1
√
2π
∞
Z
−∞
iye
ity−
y
2
2
dy =
1
√
2π
∞
Z
−∞
ie
ity
d
¡
− e
−
y
2
2
¢
dy =
=
1
√
2π
·
− ie
ity−
y
2
2
¯
¯
¯
¯
∞
−∞
−
∞
Z
−∞
te
ity−
y
2
2
dy
¸
= −tϕ
Y
(t),
т. е. [ln ϕ
Y
(t)]
0
= −t. Отсюда получаем
ln ϕ
Y
(t) = −
t
2
2
+ C.
Поскольку ϕ
Y
(0) = 1, то C = 0,
ϕ
Y
(t) = e
−
t
2
2
, ϕ
X
(t) = e
iαt−
σ
2
t
2
2
.
Пользуясь этой формулой, удобно находить моменты случайной величины X.
Далее мы установим взаимно однозначное соответствие между функциями рас-
пределения и характеристическими функциями.
Теорема (формула обращения). Если F — функция распределения, а ϕ — соот-
ветствующая ей х. ф., то для любых точек непрерывности x и y функции F
F (y ) − F(x) =
1
2π
lim
σ→0
∞
Z
−∞
e
−itx
− e
−ity
it
ϕ(t)e
−t
2
σ
2
dt.
84

Замечание. Если функция ϕ(t)/t интегрируема на бесконечности, то становит-
ся законным предельный переход под знаком интеграла в этой формуле, и можно
записать
F (y) −F (x) =
1
2π
∞
Z
−∞
e
−itx
− e
−ity
it
ϕ(t)dt.
Доказательство теоремы. Предположим сначала, что существует плотность f(y) =
F
0
(y), а х.ф. ϕ(t) интегрируема. Тогда можно воспользоваться формулой для обрат-
ного преобразования Фурье
f(u) =
1
2π
∞
Z
−∞
e
−itu
ϕ(t)dt
и
F (y) −F (x) =
y
Z
x
f(u)du =
1
2π
y
Z
x
∞
Z
−∞
e
−itu
ϕ(t)dtdu =
=
1
2π
∞
Z
−∞
y
Z
x
e
−itu
duϕ(t)dt =
1
2π
∞
Z
−∞
e
−itx
− e
−ity
it
ϕ(t)dt.
Перемена порядка интегрирования здесь возможна в силу интегрируемости функ-
ции ϕ(t).
Пусть теперь ϕ(t) — х. ф. величины X с произвольным распределением F . Рас-
смотрим на одном вероятностном пространстве с X случайную величину Y , незави-
симую от X и распределенную нормально с параметрами (0, 1). Пусть
Z
k
= σ
k
√
2Y ⊂= Φ
0,2σ
2
k
.
Если σ
k
→ 0, то почти наверное Z
k
→ 0 и X + Z
k
→ X. Следовательно, F
X+Z
k
⇒ F
X
.
С другой стороны, случайная величина X + Z
k
будет обладать плотностью и ее х.
ф., равная ϕ(t)e
−t
2
σ
2
k
, интегрируема. Поэтому
F
X+Z
k
(y) − F
X
k
+Z
(x) =
1
2π
∞
Z
−∞
e
−itx
− e
−ity
it
ϕ(t)e
−t
2
σ
2
k
dt.
Если x и y — точки непрерывности F , то F (y) − F (x) = lim
σ
k
→0
F
X+Z
k
(y) − F
X+Z
k
(x).
Отсюда следует утверждение теоремы.
Следствие 1. Х. ф. случайной величины однозначно определяет ее функцию
распределения.
Доказательство следует из формулы обращения и из того, что разности F (y)−F (x)
однозначно определяют F . Достаточно для этого в формуле обращения устремить
x → −∞.
Следствие 2. Пусть X
1
⊂= Π
λ
1
, X
2
⊂= Π
λ
2
, X
1
и X
2
независимы, тогда
X
1
+ X
2
⊂= Π
λ
1
+λ
2
.
Этот факт уже доказывался ранее прямыми вычислениями. Теперь мы приводим
новое доказательство:
ϕ
X
1
+X
2
(t) = exp{λ
1
(e
it
− 1)}exp{λ
2
(e
it
− 1)} = exp{(λ
1
+ λ
2
)(e
it
− 1)},
что соответствует распределению Π
λ
1
+λ
2
.
85

Следствие 3. Пусть X
1
и X
2
независимы, X
1
⊂= Φ
α
1
, σ
2
1
, X
2
⊂= Φ
α
2
, σ
2
2
. Тогда
X
1
+ X
2
⊂= Φ
α
1
+α
2
, σ
2
1
+σ
2
2
.
Доказательство.
ϕ
X
1
+X
2
(t) = e
iα
1
t−
σ
2
1
t
2
2
e
iα
2
t−
σ
2
2
t
2
2
= e
i(α
1
+α
2
)t−
(σ
2
1
+σ
2
2
)t
2
2
,
что соответствует распределению Φ
α
1
+α
2
, σ
2
1
+σ
2
2
.
Если X — целочисленная случайная величина, то удобнее работать с производя-
щей функцией, которая получается из х. ф. заменой z = it:
ψ
X
(z) = Ez
X
=
∞
X
k=1
z
k
P(X = k), |z| = 1.
Очевидно, производящая функция представляет собой ряд Лорана. Для нахож-
дения его коэффициентов можно воспользоваться известной формулой
P(X = k) =
1
2πi
Z
|z|=1
ψ
X
(z)z
−k−1
dz,
которая также может восприниматься как вариант формулы обращения.
Теорема о непрерывном соответствии. Пусть {F
n
} — последовательность
функций распределения, а {ϕ
n
} — соответствующая ей последовательность х. ф.
Тогда для сходимости F
n
⇒ F , где F — функция распределения, необходимо и до-
статочно, чтобы ϕ
n
(t) → ϕ(t) при каждом t, где ϕ — х. ф., соответствующая
распределению F .
Доказательство. Необходимость устанавливается просто: при каждом t функции
cos ty и sin ty непрерывны и ограничены, поэтому
∞
Z
−∞
cos ty dF
n
(y) →
∞
Z
−∞
cos ty dF (y),
∞
Z
−∞
sin ty dF
n
(y) →
∞
Z
−∞
sin ty dF (y),
и, следовательно,
ϕ
n
(t) =
∞
Z
−∞
cos ty dF
n
(y) + i
∞
Z
−∞
sin ty dF
n
(y) →
∞
Z
−∞
cos ty dF (y) + i
∞
Z
−∞
sin ty dF (y) = ϕ(t).
Доказательство достаточности проведем в несколько этапов. Обозначим C
0
мно-
жество непрерывных финитных (т. е. обращающихся в 0 вне некоторого отрезка)
функций и будем писать просто
R
, если интегрирование проводится по всей веще-
ственной оси.
Лемма 1. Пусть
R
g dF
n
→
R
g dF для любой функции g ∈ C
0
. Тогда F
n
⇒ F .
Доказательство. Для произвольного ε > 0 выберем g
ε
∈ C
0
так, чтобы
0 ≤ g
ε
(y) ≤ 1,
Z
(1 −g
ε
(y))dF (y) ≤ ε.
86
Это всегда можно сделать, положив g
ε
(y) = 1 при y ∈ [−N, N] и 0 ≤ g
ε
(y) ≤ 1 при
|y| > N (с сохранением финитности), где число N настолько велико, что F (−N) +
1 −F (N) < ε.
Возьмем теперь произвольную непрерывную ограниченную функцию g,
|g(y)| ≤ K < ∞. Тогда gg
ε
∈ C
0
и
¯
¯
¯
¯
Z
(1 −g
ε
)g dF
n
¯
¯
¯
¯
≤ K
µ
1 −
Z
g
ε
dF
n
¶
→ K
µ
1 −
Z
g
ε
dF
¶
≤ Kε.
Поэтому
lim sup
¯
¯
¯
¯
Z
g dF
n
−
Z
g dF
¯
¯
¯
¯
≤
≤ lim sup
½
¯
¯
¯
¯
Z
(1 −g
ε
)g dF
n
¯
¯
¯
¯
+
¯
¯
¯
¯
Z
gg
ε
dF
n
−
Z
gg
ε
dF
¯
¯
¯
¯
+
¯
¯
¯
¯
Z
(1 −g
ε
)g dF
¯
¯
¯
¯
¾
≤ 2Kε.
Лемма доказана.
Обозначим C
0
k
множество всех финитных k раз непрерывно дифференцируемых
функций, k ≥ 1.
Лемма 2. Пусть
R
g dF
n
→
R
g dF для любой функции g ∈ C
0
k
при некотором
k ≥ 1. Тогда F
n
⇒ F .
Доказательство. Любую функцию g ∈ C
0
можно равномерно приблизить функ-
цией ˜g ∈ C
0
k
. К примеру, можно воспользоваться следующим процессом. Поскольку
для любого ε > 0 найдется δ = δ(ε) > 0 такое, что |g(u) − g(y) | < ε при |u − y| < δ
(свойство равномерной непрерывности g), то положив
˜g(y) =
1
2δ
y+δ
Z
y−δ
g(u) du,
будем иметь
|˜g(y) − g(y)| ≤
1
2δ
y+δ
Z
y−δ
|g(u) − g(y)|du ≤ ε.
Функция ˜g уже будет непрерывно дифференцируемой и по-прежнему финитной. По-
вторив эту операцию дважды, получим дважды непрерывно дифференцируемую фи-
нитную функцию и т. д. Итак, пусть g ∈ C
0
, ˜g ∈ C
0
k
такие, что |˜g(y) − g(y)| ≤
ε
3
,
тогда для всех достаточно больших n
¯
¯
¯
¯
Z
g dF
n
−
Z
g dF
¯
¯
¯
¯
≤
¯
¯
¯
¯
Z
(g − ˜g) dF
n
¯
¯
¯
¯
+
¯
¯
¯
¯
Z
˜g dF
n
−
Z
˜g dF
¯
¯
¯
¯
+
¯
¯
¯
¯
Z
(g − ˜g) dF
¯
¯
¯
¯
≤ ε.
Лемма доказана.
Лемма 3 (равенство Парсеваля). Пусть g ∈ C
0
k
при некотором k ≥ 2, X ⊂= F ,
тогда
Eg(X) =
Z
g(y)dF (y) =
1
2π
Z
ϕ(−t)ˆg(t)dt,
где ϕ(t) = Ee
itX
, ˆg(t) =
R
e
ity
g(y)dy.
Если F имеет плотность f = F
0
, то мы получаем равенство Парсеваля в более
привычном виде
Z
g(y)f(y)dy =
1
2π
Z
ϕ(−t)ˆg(t)dt.
87
Доказательство. Для функции g ∈ C
0
k
имеем
ˆg(t) =
∞
Z
−∞
e
ity
g(y)dy =
∞
Z
−∞
g(y)d
µ
e
ity
it
¶
=
·
g(y)e
ity
it
¯
¯
¯
¯
∞
−∞
−
1
it
∞
Z
−∞
e
ity
g
0
(y)dy
¸
=
= −
1
it
∞
Z
−∞
e
ity
g
0
(y)dy = . . . =
(−1)
k
(it)
k
∞
Z
−∞
e
ity
g
(k)
(y)dy.
Отсюда
|ˆg(t)| ≤
C
|t|
k
, k ≥ 2,
поэтому ˆg(t) — абсолютно интегрируемая на бесконечности функция. Воспользуемся
формулой обратного преобразования Фурье:
g(y) =
1
2π
Z
e
−ity
ˆg(t)dt,
откуда
Eg(X) = E
1
2π
Z
e
−itX
ˆg(t)dt =
1
2π
Z
Ee
−itX
ˆg(t)dt =
1
2π
Z
ϕ
X
(−t)ˆg(t)dt.
Лемма доказана.
Перейдем теперь непосредственно к доказательству теоремы о непрерывном со-
ответствии. Пусть ϕ
n
(t) → ϕ(t) при всех t. Тогда для всякой g ∈ C
0
k
при k ≥ 2 имеет
место
Z
g(y) dF
n
(y) =
1
2π
Z
ϕ
n
(−t)ˆg(t)dt,
и функция |ϕ
n
(−t)ˆg(t)| ≤ |ˆg(t)| интегрируема. По теореме о мажорируемой сходимо-
сти правая часть сходится к
1
2π
Z
ϕ(−t)ˆg(t)dt =
Z
g(y) dF (y).
Теорема доказана.
Вернемся к закону больших чисел. Мы его доказали ранее при условии, что слу-
чайные величины X
n
обладают конечным вторым моментом. Пользуясь аппаратом
характеристических функций, мы можем получить более сильное утверждение.
Теорема Хинчина (закон больших чисел). Пусть случайные величины X
1
, X
2
, . . .
независимы и одинаково распределены, причем E|X
1
| < ∞. Обозначим a = EX
1
,
S
n
=
P
n
i=1
X
i
. Тогда при n → ∞
S
n
n
P
→ a.
Доказательство. Поскольку речь идет о сходимости к константе, достаточно до-
казать, что F
S
n
/n
⇒ I
a
, а для этого, в свою очередь, необходимо и достаточно, чтобы
ϕ
S
n
/n
(t) → e
ita
.
Имеем для каждого фиксированного t
ϕ
S
n
/n
(t) = ϕ
S
n
¡
t/n
¢
=
·
1 +
ita
n
+ o
µ
t
n
¶¸
n
,
ln ϕ
S
n
/n
(t) = n ln
µ
1 +
ita
n
+ o
µ
t
n
¶¶
= n
µ
ita
n
+ o
µ
t
n
¶¶
→ ita.
Теорема доказана.
88
4.5. Центральная предельная теорема
Как и ранее, будем иметь дело с последовательностью X
1
, X
2
, . . . независимых
одинаково распределенных случайных величин, S
n
= X
1
+ . . . + X
n
.
Во многих прикладных задачах возникает необходимость вычислять вероятности
вида P(A ≤ S
n
≤ B) при больших n. Это происходит, например, при планировании
производства, поскольку общая выработка продукции предприятием за смену скла-
дывается из случайных объемов продукции, произведенных отдельными рабочими.
Вычисление различных средних показателей в экономике, социологии, демографии,
статистике также сводится к суммированию случайных величин.
Мы видели, что для нахождения распределения суммы двух независимых случай-
ных величин следует пользоваться формулой свертки. Однако ее применение сопря-
жено с непростыми вычислениями, в особенности если мы интересуемся распреде-
лением суммы большого числа слагаемых. Более продуктивными оказались методы
приближенного вычисления указанных вероятностей для сумм.
Мы знаем, что для нахождения вероятности попадания суммы в интервал (или
отрезок) достаточно знать ее функцию распределения. Значит, необходимо искать
приближения для функций распределения сумм. Оказалось, что в широких услови-
ях функции распределения немного подправленных (а точнее стандартизованных)
сумм случайных величин сближаются с функцией распределения стандартного нор-
мального закона, если число слагаемых возрастает.
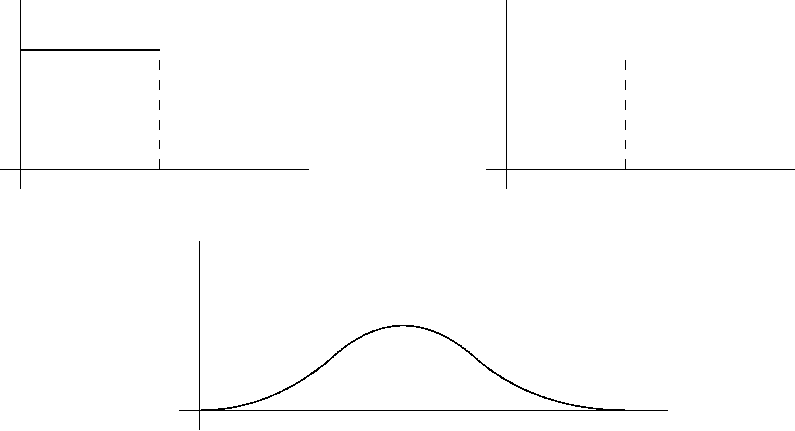
Этот эффект можно наблюдать на примерах. Пусть все X
i
независимы и имеют
равномерное на [0,1] распределение. Вычислим с помощью сверток плотности рас-
пределения случайных величин X
1
+ X
2
, X
1
+ X
2
+ X
3
(это нетрудно) и увидим,
что их графики очень быстро начинают напоминать плотность нормального распре-
деления:
-
6
0 1
t
f
X
1
(t)
-
6
0 1 2
t
f
X
1
+X
2
(t)
¡
¡
¡
¡
¡
¡@
@
@
@
@
@
-
6
0 1 2 3
t
f
X
1
+X
2
+X
3
(t)
Последний график получается склеиванием трех квадратических парабол. Для
f
X
1
+X
2
+X
3
+X
4
(t) график будет склеиваться из кубических парабол; уже для суммы
пяти случайных величин на глаз трудно различить график полученной плотности
от гауссовской кривой.
Такую же закономерность мы можем наблюдать, если рисовать графики плот-
ности сумм в том случае, когда все X
i
⊂= E
α
. Тогда, как мы видели, S
n
⊂= Γ
α,n
,
89
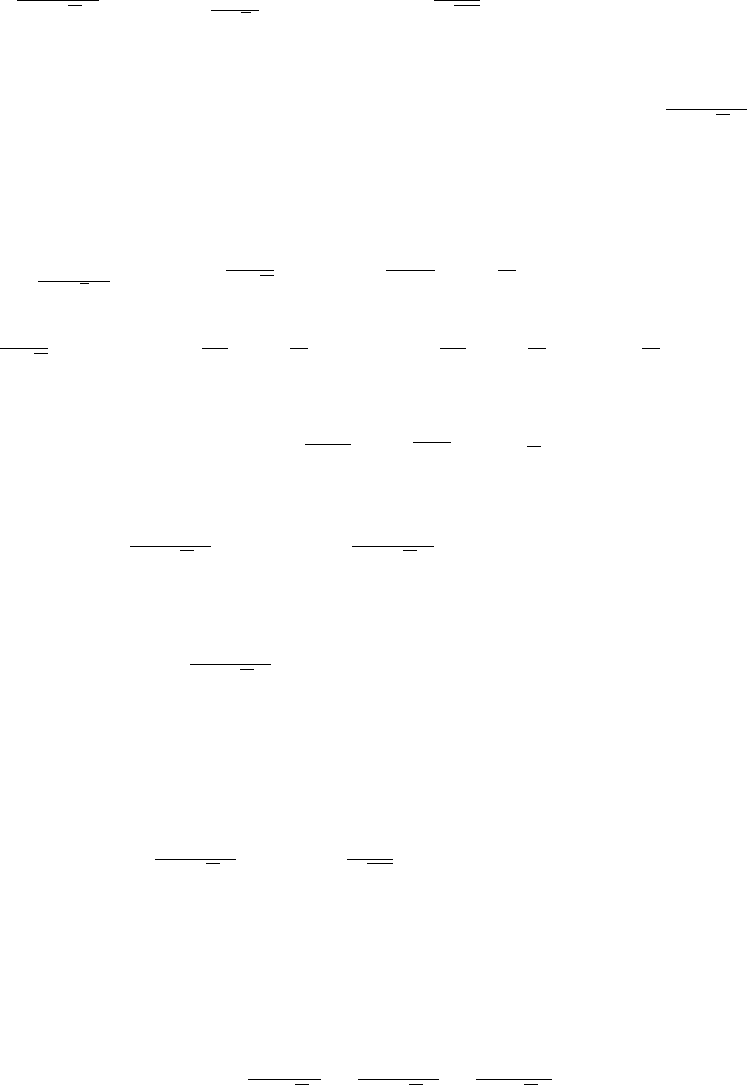
и при больших значениях n кривая плотности гамма-распределения, растягиваясь
вправо, все больше будет напоминать плотность нормального распределения, толь-
ко сильно вытянутую и смещенную вправо. Чтобы в пределе получалась плотность
стандартного нормального закона, суммы надо подправлять с помощью операции
стандартизации.
Эти наблюдения иллюстрируют важную закономерность, о которой пойдет речь
ниже.
Центральная предельная теорема (ЦПТ). Пусть X
1
, X
2
. . . — независимые
одинаково распределенные случайные величины. Предположим, что EX
2
1
< ∞. Обо-
значим S
n
= X
1
+ . . . + X
n
, a = EX
1
, σ
2
= DX
1
, и пусть σ
2
> 0. Тогда для любого y
P
µ
S
n
− na
σ
√
n
< y
¶
= F
S
n
−na
σ
√
n
(y) → Φ
0,1
(y) =
1
√
2π
y
Z
−∞
e
−t
2
/2
dt
при n → ∞.
Доказательство. Достаточно доказать, что х. ф. случайной величины
S
n
− na
σ
√
n
сходится к exp{−t
2
/2}, т. е. к х. ф. стандартного нормального распределения. Обо-
значим для удобства Y
k
= X
k
− a, k = 1, 2, . . .. Тогда EY
k
= 0, DY
k
= DX
k
= σ
2
,
S
n
− na = Y
1
+ . . . + Y
n
,
ϕ
Y
1
+...+Y
n
σ
√
n
(t) = ϕ
n
Y
1
µ
t
σ
√
n
¶
=
µ
1 −
σ
2
t
2
2σ
2
n
+ o
µ
t
2
n
¶¶
n
,
ln ϕ
n
Y
1
µ
t
σ
√
n
¶
= n ln
µ
1 −
t
2
2n
+ o
µ
t
2
n
¶¶
= n
µ
−
t
2
2n
+ o
µ
t
2
n
¶¶
→ −
t
2
2
.
Теорема доказана.
Замечания
1. Нетрудно видеть, что ES
n
= na,
√
DS
n
=
√
nσ
2
= σ
√
n, т. е. к случайной
величине S
n
в теореме применена операция стандартизации;
E
µ
S
n
− na
σ
√
n
¶
= 0, D
µ
S
n
− na
σ
√
n
¶
= 1.
2. Сходимость в ЦПТ является равномерной по всем y, т. е.
sup
y
¯
¯
¯
¯
P
µ
S
n
− na
σ
√
n
< y
¶
− Φ
0,1
(y)
¯
¯
¯
¯
→ 0
при n → ∞. Как мы видели ранее, это следует из непрерывности предельной функ-
ции распределения.
3. Можно сформулировать ЦПТ в эквивалентной форме: для любых A ≤ B
P
µ
A ≤
S
n
− na
σ
√
n
≤ B
¶
→
1
√
2π
B
Z
A
e
−t
2
/2
dt.
Именно такая форма чаще всего используется при решении задач. Делается это
следующим образом. Предположим, что нам необходимо найти вероятность
P(C ≤ S
n
≤ D) при больших значениях n. Первое, что мы должны сделать, это
подогнать наше выражение под формулировку теоремы:
P(C ≤ S
n
≤ D) = P
µ
C − na
σ
√
n
≤
S
n
− na
σ
√
n
≤
D − na
σ
√
n
¶
,
90
