Лотов В.И. Теория вероятностей. Конспект лекций
Подождите немного. Документ загружается.

Свойства коэффициента корреляции
1. |ρ(X, Y )| ≤ 1.
Это свойство напрямую получается из неравенства Коши-Буняковского.
2. |ρ(X, Y )| = 1 тогда и только тогда, когда для некоторых констант a 6= 0 и b
выполняется Y = aX + b.
Доказательство. Если Y = aX + b, то
ρ(X, Y ) =
E((X − EX)(aX + b − E(aX + b)))
p
DX D(aX + b)
=
=
E((X − EX)(aX + b − aEX − b))
p
DX a
2
DX)
=
aE(X − EX)
2
|a|DX
=
a
|a|
= ±1
в зависимости от знака числа a.
Для доказательства обратного утверждения введем случайные величины
X
1
=
X − EX
√
DX
, Y
1
=
Y − EY
√
DY
.
Здесь к каждой случайной величине применена операция стандартизации, которая
состоит в вычитании матожидания и делении на корень квадратный из дисперсии.
Она производится с единственной целью: добиться, чтобы математическое ожидание
стало нулевым, а дисперсия — единичной. Действительно,
EX
1
=
1
√
DX
E(X − EX) = 0, D X
1
=
µ
1
√
DX
¶
2
D(X − EX) =
DX
DX
= 1.
Кроме того,
ρ(X, Y ) = EX
1
Y
1
= Cov(X
1
, Y
1
).
Таким образом,
D(Y
1
± X
1
) = DX
1
+ DY
1
± 2Cov(X
1
, Y
1
) = 2 ± 2ρ(X, Y ).
Пусть теперь, к примеру, ρ(X , Y ) = 1. Воспользуемся полученным соотношением:
D(Y
1
− X
1
) = 2 − 2ρ(X, Y ) = 0.
В силу свойств дисперсии это означает, что Y
1
−X
1
= 0 с вероятностью единица или,
что то же самое,
Y =
√
DY
√
DX
X + EY −
√
DY EX
√
DX
.
Если ρ(X, Y ) = −1, то пользуемся соотношением
D(Y
1
+ X
1
) = 2 + 2ρ(X, Y ) = 0.
3. Если X и Y независимы, то ρ(X, Y ) = 0.
Свойство очевидно.
К сожалению, обратное утверждение не имеет места.
4. Если ρ(X, Y ) = 0, то X и Y не обязательно независимы.
Пример этому уже приводился: если X ⊂= U
−1,1
и Y = X
2
, то Cov(X, Y ) =
ρ(X, Y ) = 0, хотя случайные величины зависимы.
По этой причине случайные величины X и Y называются некоррелированными,
если ρ(X, Y ) = 0. Независимость влечет некоррелированность, но не наоборот.
61
3.5. Многомерный случай: математическое ожидание
и матрица ковариаций
В этом разделе мы обобщим понятия математического ожидания и дисперсии на
многомерный случай.
Пусть
X =
X
11
X
12
. . . X
1n
X
21
X
22
. . . X
2n
. . . . . . . . . . . .
X
m1
X
m2
. . . X
mn
— матрица, составленная из случайных величин. Положим, по определению,
EX =
EX
11
EX
12
. . . EX
1n
EX
21
EX
22
. . . EX
2n
. . . . . . . . . . . .
EX
m1
EX
m2
. . . EX
mn
.
Легко проверить, что при таком определении сохраняются следующие свойства ма-
тематических ожиданий.
1. Если A и B — матрицы, составленные из констант, то E(AX) = AEX,
E(XB) = (EX)B.
2. E(X + Y ) = EX + EY .
3. Если любой элемент матрицы X не зависит от любого элемента матрицы Y , то
E(XY ) = EXEY .
Разумеется, мы предполагаем, что размерности участвующих здесь матриц поз-
воляют применять операции сложения и умножения.
Аналог дисперсии вводится только для случайных векторов. На протяжении этого
и следующего параграфов мы будем изображать векторы в виде столбцов
X =
X
1
X
2
. . .
X
n
.
Определение. Матрицей ковариаций случайного вектора X называется матри-
ца C(X), у которой на месте с номером (i, j) стоит c
i,j
= Cov(X
i
, X
j
), i, j = 1, . . . , n.
Матрица ковариаций есть аналог дисперсии. При n = 1 она совпадает с диспер-
сией. В общем случае на главной диагонали у нее стоят дисперсии DX
1
, . . . , DX
n
,
матрица симметрична относительно главной диагонали: c
i,j
= c
j,i
.
Мы знаем, что D(AX+B) = A
2
DX в одномерном случае, если A и B — константы.
Аналогом этого свойства для случайных векторов является следующее утверждение.
Теорема. Пусть A — матрица из констант, имеющая m строк и n столбцов,
а B — вектор из констант размерности m. Тогда
C(AX + B) = AC(X)A
T
,
где верхний индекс T соответствует транспонированной матрице.
Доказательство. Обозначим для краткости m
i
= EX
i
, i = 1, . . . , n, и воспользу-
емся следующим свойством произведения матриц: если умножить вектор-столбец на
62

вектор-строку, то в итоге получим матрицу:
X
1
− m
1
X
2
− m
2
. . .
X
n
− m
n
· (X
1
− m
1
, X
2
− m
2
, . . . , X
n
− m
n
) =
=
(X
1
− m
1
)
2
(X
1
− m
1
)(X
2
− m
2
) . . . (X
1
− m
1
)(X
n
− m
n
)
(X
2
− m
2
)(X
1
− m
1
) (X
2
− m
2
)
2
. . . (X
2
− m
2
)(X
n
− m
n
)
. . . . . . . . . . . .
(X
n
− m
n
)(X
1
− m
1
) (X
n
− m
n
)(X
2
− m
2
) . . . (X
n
− m
n
)
2
.
Взяв теперь математическое ожидание от обеих частей, получим
E(X − EX)(X − EX)
T
= C(X),
и аналогично
C(AX + B) = E(AX + B − E(AX + B))(AX + B − E(AX + B))
T
=
= E(AX + B − EAX − B)(AX + B − EAX − B)
T
=
= E(A(X − EX)(X − EX)
T
A
T
) =
= A(E(X − EX)(X − EX)
T
)A
T
= AC(X)A
T
.
Теорема доказана.
3.6. Многомерное нормальное распределение
Мы уже рассматривали ранее в качестве примера частный случай плотности
многомерного нормального закона, она соответствовала стандартному многомерно-
му нормальному распределению. Сейчас введем этот закон распределения в общей
форме.
Будем действовать по аналогии с одномерным случаем.
Пусть Y — одномерная случайная величина, имеющая стандартное нормальное
распределение, Y ⊂= Φ
0,1
. Взяв произвольные числа α и σ > 0, образуем случайную
величину X = σY +α, которая уже будет распределена по закону Φ
α,σ
2
с плотностью
ϕ
α,σ
2
(t) =
1
σ
√
2π
e
−(t−α)
2
/2σ
2
, −∞ < t < ∞.
Тем самым мы получили общий вид плотности нормального распределения с помо-
щью линейных преобразований над случайной величиной Y , имеющей стандартное
нормальное распределение.
Так же поступим и в многомерном случае. Пусть Y — случайный вектор с коор-
динатами Y
1
, . . . , Y
n
, имеющий многомерное стандартное нормальное распределение
с плотностью
f
Y
(t) =
1
(2π)
n/2
exp
(
−
1
2
n
X
i=1
t
2
i
)
=
1
(2π)
n/2
exp
½
−
1
2
t
T
t
¾
=
n
Y
i=1
ϕ
0,1
(t
i
).
Последнее означает, что координаты вектора Y
1
, . . . , Y
n
независимы и одинаково рас-
пределены в соответствии со стандартным нормальным законом. Здесь C(Y ) = E —
единичная матрица, t = (t
1
, . . . , t
n
)
T
— вектор-столбец.
63
Возьмем произвольную невырожденную матрицу A размерности n×n, состоящую
из констант, и постоянный вектор α = (α
1
, . . . , α
n
)
T
и образуем новый случайный
вектор
X = AY + α.
Распределение получившегося вектора X и будем называть многомерным нормаль-
ным распределением.
Теорема. Плотность многомерного нормального распределения задается фор-
мулой
f
X
(t) =
√
det Q
(2π)
n/2
exp
©
−(t −α)
T
Q(t −α)/2
ª
,
где t = (t
1
, . . . , t
n
)
T
, Q = (C(X))
−1
= (AC(Y )A
T
)
−1
= (AA
T
)
−1
.
Заметим, что при n = 1 и A = σ получаем Q = 1/σ
2
,
√
det Q = 1/σ.
Доказательство. Какой бы прямоугольник B ⊂ R
n
ни взять, по основному свой-
ству плотностей должно быть
P(X ∈ B) =
Z
B
f
X
(t)dt,
здесь для краткости обозначено dt = dt
1
dt
2
. . . dt
n
. В то же время
P(AY + α ∈ B) = P(Y ∈ A
−1
(B − α)) =
Z
A
−1
(B−α))
f
Y
(u)du,
где под множеством A
−1
(B −α) понимается совокупность всех точек u : Au + α ∈ B.
Для того чтобы преобразовать этот интеграл к нужному нам интегралу по множеству
B (и тогда стоящая под интегралом функция и будет искомой плотностью), сделаем
замену переменных t = Au + α. В результате этой замены множество A
−1
(B − α)
перейдет в B, u — в A
−1
(t −α), exp
©
−
1
2
u
T
u
ª
перейдет в
exp
½
−
1
2
(t −α)
T
(A
−1
)
T
A
−1
(t −α)
¾
= exp
½
−
1
2
(t −α)
T
(AA
T
)
−1
(t −α)
¾
.
При переходе от du к dt появится якобиан
√
det Q.
Таким образом, под интегралом появится функция, присутствующая в утвержде-
нии теоремы — она и будет плотностью вектора X. Теорема доказана.
Для нас большую важность представляют следующие два следствия из этой тео-
ремы.
Следствие 1. Пусть случайный вектор X = (X
1
, X
2
, . . . , X
n
)
T
имеет много-
мерное нормальное распределение и все его компоненты попарно некоррелированны.
Тогда они независимы.
Доказательство. Вследствие некоррелированности компонент заключаем, что
матрица ковариаций C(X) имеет диагональный вид: на главной диагонали стоят
дисперсии DX
1
, . . . , DX
n
, а все остальные элементы равны нулю. Обозначим для
краткости σ
2
i
= DX
i
, i = 1, . . . , n. Тогда матрица Q = (C(X))
−1
также будет диа-
гональной, у нее на главной диагонали будут стоять числа σ
−2
1
, . . . , σ
−2
n
. По этой
причине плотность распределения вектора X приобретает вид
f
X
(t) =
1
σ
1
. . . σ
n
(2π)
n/2
exp
(
−
n
X
i=1
(t
i
− α
i
)
2
2σ
2
i
)
=
n
Y
i=1
ϕ
α
i
σ
2
i
(t
i
),
64

что эквивалентно независимости компонент вектора X.
Следствие 2. Пусть случайный вектор X = (X
1
, X
2
, . . . , X
n
)
T
имеет мно-
гомерное стандартное нормальное распределение (напомним: это соответствует
тому, что все компоненты вектора независимы и имеют распределение Φ
0,1
). Об-
разуем новый вектор Y = AX, где A — ортогональная матрица. Тогда вектор Y
также будет иметь многомерное стандартное нормальное распределение.
Доказательство. Ортогональная матрица, по определению, обладает свойством
A
T
= A
−1
. По этой причине C(Y ) = AC(X)A
T
= AA
T
= E и, следовательно,
f
Y
(t) =
1
(2π)
n/2
exp
½
−
1
2
t
T
t
¾
=
n
Y
i=1
ϕ
0,1
(t
i
) = f
X
(t),
что и требовалось доказать.
3.7. Математическое ожидание суммы случайного числа
слагаемых
Ранее было введено понятие σ-алгебры σ(X) = { X
−1
(B), B ∈ B(R)}, порож-
денной случайной величиной X. Она состоит из событий, о реализации которых
можно судить по значениям X. Пусть имеется теперь последовательность случай-
ных величин {X
n
}. Для любых k ≤ m ≤ ∞ введем σ-алгебру σ(X
k
, . . . , X
m
), которая
порождена событиями вида
T
m
i=k
A
i
, где A
i
∈ σ(X
i
). Это более богатая σ-алгебра,
чем, к примеру, σ(X
k
) или σ(X
k
, . . . , X
m−1
), так как некоторые из множеств A
i
могут
совпадать с Ω.
Теорема. Если случайные величины X
1
, X
2
, . . . независимы, то для любых k ≥ 1,
n ≥ 1 σ-алгебры σ(X
1
, . . . , X
n
) и σ(X
n+k
, X
n+k+1
, . . .) независимы.
Схема доказательства состоит в следующем. Сначала проверяется независимость
произвольного события вида
T
n
i=1
A
i
и события вида
T
m
i=n+k
A
i
, где A
i
∈ σ(X
i
),
n + k ≤ m < ∞. Затем устанавливается независимость алгебр, порожденных со-
бытиями такого вида. Переход к пределу при m → ∞ осуществляется с помощью
свойства непрерывности вероятности. Как уже доказано ранее, независимость алгебр
обеспечивает независимость порожденных ими σ-алгебр.
Пусть на вероятностном пространстве < Ω, S, P > задана последовательность
{X
n
} независимых случайных величин и некоторая целочисленная случайная вели-
чина ν ≥ 0. Значения n можно интерпретировать как дискретные моменты времени.
Определение. Случайная величина ν ≥ 0 называется не зависящей от будуще-
го, если для любого n событие {ν ≤ n} не зависит от σ-алгебры σ(X
n+1
, X
n+2
, . . .).
Определение. Если {ν ≤ n} ∈ σ(X
1
, . . . , X
n
) при всех n , то такая случайная
величина ν называется марковской или марковским моментом.
Ясно, что марковский момент не зависит от будущего, так как σ(X
1
, . . . , X
n
) и
σ(X
n+1
, X
n+2
, . . .) независимы.
Примерами марковских моментов могут служить случайные величины
ν
1
= inf{k ≥ 1 : X
k
≥ N},
поскольку
{ν
1
≤ n} =
n
\
k=1
{X
k
≥ N} ∈ σ(X
1
, . . . , X
n
),
а также
ν
2
= inf{k ≥ 1 : S
k
≥ N},
65
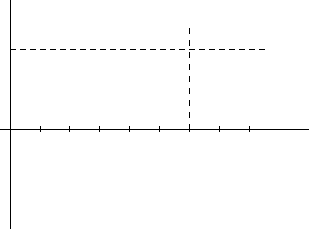
где S
k
= X
1
+ . . . + X
k
, N > 0 — произвольное положительное число.
-
6
0
N
k
S
k
ν
2
1 2 3
¡
¡
A
A
A
A
H
H
¡
¡
@
@
¥
¥
¥
¥
¥
¥
¥
¥
Теорема (Колмогоров - Прохоров). Пусть целочисленная случайная величи-
на ν ≥ 0 не зависит от будущего. Тогда если
∞
X
k=1
P(ν ≥ k)E|X
k
| < ∞,
то
ES
ν
=
∞
X
k=1
P(ν ≥ k)EX
k
.
Доказательство. Предположим сначала, что все случайные величины X
k
неотри-
цательны. Тогда вне зависимости от того, конечно ES
ν
или нет, мы можем написать
ES
ν
=
∞
X
n=1
E(S
ν
; ν = n) =
∞
X
n=1
E(S
n
; ν = n) =
=
∞
X
n=1
n
X
k=1
E(X
k
; ν = n) =
∞
X
k=1
∞
X
n=k
E(X
k
; ν = n) =
∞
X
k=1
E(X
k
; ν ≥ k).
Событие {ν ≥ k} = {ν > k − 1} = Ω \ { ν ≤ k − 1} не зависит от σ-алгебры
σ(X
k
, X
k+1
, . . .), поэтому оно не зависит от σ(X
k
). Значит,
E(X
k
; ν ≥ k) = EX
k
I
{ν≥k}
= EX
k
EI
{ν≥k}
= EX
k
P(ν ≥ k)
и ES
ν
=
P
∞
k=1
P(ν ≥ k)EX
k
< ∞.
Если X
k
могут принимать значения разных знаков, то, очевидно,
E|S
ν
| ≤ E
ν
X
k=1
|X
k
| =
∞
X
k=1
P(ν ≥ k)E|X
k
| < ∞,
и мы вновь можем повторить наши рассуждения, обосновав перемену порядка сум-
мирования абсолютной сходимостью ряда
∞
X
k=1
∞
X
n=k
|E(X
k
; ν = n)| ≤
∞
X
k=1
∞
X
n=k
E(|X
k
|; ν = n) ≤
≤
∞
X
k=1
E(|X
k
|; ν ≥ k) =
∞
X
k=1
E|X
k
|P(ν ≥ k) < ∞.
66

Следствие (тождество Вальда). Если X
1
, X
2
, . . . — независимые одинаково распре-
деленные случайные величины, E|X
1
| < ∞, ν не зависит от будущего и Eν < ∞,
то ES
ν
= EX
1
Eν.
Доказательство. Достаточно заметить, что
∞
X
k=1
P(ν ≥ k) =
∞
X
k=1
∞
X
i=k
P(ν = i) =
∞
X
i=1
iP(ν = i) = Eν.
В качестве примера использования тождества Вальда рассмотрим задачу о разо-
рении.
Два игрока, A и B, подбрасывают монету, и в случае выпадения герба A выигры-
вает единицу, если решка, то единицу выигрывает B. Это так называемая безобидная
игра, игроки каждый раз выигрывают единицу с равной вероятностью. Пусть a и b
— начальные капиталы игроков. Игра заканчивается, когда один из игроков про-
играет весь свой капитал. Обозначим P
A
и P
B
вероятности разорения для A и B
соответственно. Наша задача — найти эти вероятности.
Если обозначить X
n
выигрыш A в n-м туре (он может равняться 1 или -1 с рав-
ными вероятностями), то S
n
= X
1
+ . . . + X
n
есть суммарный выигрыш A после n
бросаний монеты. Удобно изображать развитие игры на графике.
-
6
0
b
−a
ν
n
S
n
1 2 3
¡
¡
@
@
@
@
@
@¡
¡@
@
@
@
Покажем, что P
A
+ P
B
= 1, т. е. с вероятностью единица траектория обязательно
выйдет из полосы. Действительно, для любого натурального N
1 −P
A
− P
B
= P(S
1
∈ (−a, b), S
2
∈ (−a, b), . . .) ≤
≤ P(|X
1
+ . . . + X
N
| < a + b, |X
N+1
+ . . . + X
2N
| < a + b, . . .) =
= P(|X
1
+ . . . + X
N
| < a + b)P(|X
N+1
+ . . . + X
2N
| < a + b) . . . = 0,
если N таково, что P(|X
1
+ . . . + X
N
| < a + b) < 1. Но для этого достаточно взять
N = a + b, так как при этом
P(|X
1
+ . . . + X
N
| = a + b) =
2
2
a+b
> 0
и
P(|X
1
+ . . . + X
N
| < a + b) = 1 −
2
2
a+b
< 1.
Обозначим через ν момент прекращения игры, т. е. разорения одного из игроков. Яс-
но, что ν — марковский момент; S
ν
= −a с вероятностью P
A
и S
ν
= b с вероятностью
P
B
. Поэтому в силу тождества Вальда
ES
ν
= −aP
A
+ b(1 − P
B
) = EνE X
1
= 0,
67
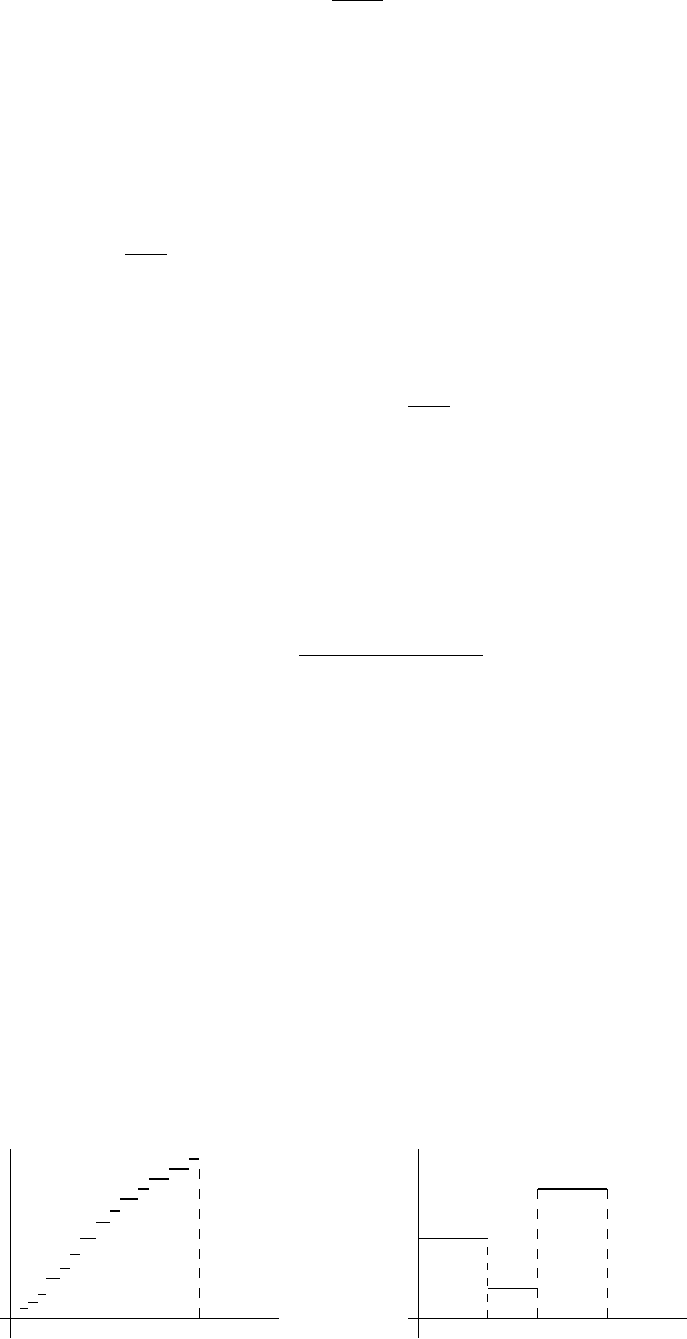
если Eν < ∞. Отсюда сразу следует P
A
=
b
a + b
. Отметим, что P
A
= 1, если b = ∞, то
есть внешне безобидная игра с бесконечно богатым соперником всегда заканчивается
разорением.
Покажем, что Eν < ∞. Вычисление вероятностей P(ν = k) является весьма
сложной задачей, поэтому мы подходящим образом оценим сверху P(ν ≥ k) и вос-
пользуемся формулой Eν =
P
∞
k=1
P(ν ≥ k). Имеем для уже выбранного числа N
P(ν ≥ mN) ≤ P(|X
1
+ . . . + X
N
| < a + b, . . . , |X
(m−1)N+1
+ . . . + X
mN
| < a + b) ≤
≤
µ
1 −
2
2
a+b
¶
m
,
Eν =
∞
X
k=1
P(ν ≥ k) =
∞
X
m=0
X
mN<k≤(m+1)N
P(ν ≥ k) ≤
≤
∞
X
m=0
NP(ν ≥ mN) ≤ N
∞
X
m=0
µ
1 −
2
2
a+b
¶
m
< ∞.
3.8. Условное математическое ожидание
Сначала введем понятие условного распределения. Пусть X и Y — две дискретные
случайные величины, заданные на одном вероятностном пространстве. Обозначим
p
X
(u/v) =
P(X = u, Y = v)
P(Y = v)
и назовем эту функцию условным распределением случайной величины X при усло-
вии Y = v. Здесь переменная v принимает только те значения, для которых
P(Y = v) > 0.
Далее рассмотрим математическое ожидание, соответствующее этому условному
распределению (если оно существует):
E(X/v) =
X
u
up
X
(u/v).
Мы получили тем самым функцию от текущего значения v случайной величины Y .
Рассматривая теперь E(X/Y ) как случайную величину, которая каждому ω ставит
в соответствие E(X/Y (ω)), мы получаем условное математическое ожидание X
относительно Y .
Проиллюстрируем введенное понятие на рисунке. Пусть, как и ранее, Ω = [0, 1],
и графики случайных величин выглядят следующим образом.
-
6
0
ω
X(ω)
1
-
6
0
ω
Y (ω)
1
А вот как выглядит график случайной величины E(X/Y ) (он показан жирной
линией):
68

-
6
0
ω
E(X/Y )
1
Случайная величина E(X/Y ) получается из X следующим образом: на каждом
из трех отрезков, где Y постоянна, X заменяется на среднее значение, вычисленное
по этому отрезку.
Из приведенного выше определения непосредственно вытекают следующие свой-
ства.
1. Если X и Y независимы, то E(X/Y ) = EX. Это очевидно.
2. Для любой борелевской функции g имеет место
E(g(Y )X/Y ) = g(Y )E(X/Y ),
т. е. g(Y ) выносится из-под знака математического ожидания подобно константе. В
частности, при X = 1 получаем E(g(Y )/Y ) = g(Y ).
Доказательство.
p
g(Y )X
(u/v) =
P(g(Y )X = u, Y = v)
P(Y = v)
=
P(g(v)X = u, Y = v)
P(Y = v)
,
поэтому
E(g(Y )X/v) =
X
u
u
P(g(v)X = u, Y = v)
P(Y = v)
=
X
t
g(v)t
P(X = t, Y = v)
P(Y = v)
= g(v)E(X/v).
3. E(X
1
+ X
2
/Y ) = E(X
1
/Y ) + E (X
2
/Y ).
Доказательство.
E(X
1
+X
2
/v) =
X
u
u
P(X
1
+ X
2
= u, Y = v)
P(Y = v)
=
X
t
1
, t
2
(t
1
+t
2
)
P(X
1
= t
1
, X
2
= t
2
, Y = v)
P(Y = v)
=
=
X
t
1
t
1
X
t
2
P(X
1
= t
1
, X
2
= t
2
, Y = v)
P(Y = v)
+
X
t
2
t
2
X
t
1
P(X
1
= t
1
, X
2
= t
2
, Y = v)
P(Y = v)
=
= E(X
1
/v) + E(X
2
/v).
4. EX = E[E(X/Y )].
Доказательство.
EX =
X
u
uP(X = u) =
X
u
u
X
v
P(X = u, Y = v)
P(Y = v)
P(Y = v) =
=
X
v
X
u
up
X
(u/v)P(Y = v) =
X
v
E(X/v)P(Y = v).
Далее введем условное математическое ожидание для случайных величин, име-
ющих абсолютно непрерывное совместное распределение.
69

Пусть f
X,Y
(u, v) — плотность совместного распределения пары случайных вели-
чин (X, Y ), f
X
(u) и f
Y
(v) — соответственно плотности случайных величин X и Y .
Для тех значений v, для которых f
Y
(v) > 0, введем условную плотность
f
X
(u/v) =
f
X,Y
(u, v)
f
Y
(v)
и математическое ожидание (если оно существует)
E(X/v) =
Z
∞
−∞
uf
X
(u/v)du.
Подставляя в это выражение Y вместо v, получим условное математическое ожида-
ние E(X/Y ).
Перечисленные выше свойства 1 – 4 сохраняются в силе и в этом случае, однако
доказательства будут выглядеть сложнее и мы их не будем приводить. Отметим
только, что во всех этих конструкциях X и Y могут быть векторными — это не
вызовет принципиальных изменений.
3.9. Задача о наилучшем приближении
В этом разделе мы будем рассматривать случайные величины, заданные на одном
вероятностном пространстве и обладающие конечным вторым моментом. Для любых
двух таких величин X, Y введем скалярное произведение (X, Y ) = E(XY ). Оно
конечно в силу неравенства Коши–Буняковского. Введем также норму
kXk
2
= (X, X) = EX
2
.
Сходимость последовательности случайных величин {X
n
} по этой норме называется
сходимостью в среднем квадратическом, kX
n
−Xk → 0 ⇐⇒ E(X
n
−X)
2
→ 0. Можно
показать, что kX
n
− Xk → 0 при n → ∞ ⇐⇒ kX
n
− X
m
k → 0 при n, m → ∞.
Пусть H — линейное пространство случайных величин с конечным вторым мо-
ментом, замкнутое относительно сходимости в среднем квадратическом. Пусть также
L — некоторое замкнутое линейное подпространство в H. Задача состоит в том, что-
бы приблизить произвольную случайную величину X ∈ H с помощью случайной
величины Y ∈ L.
Назовем
b
X ∈ L наилучшим приближением для X ∈ H, если
kX −
b
Xk = min
Y ∈L
kX − Y k.
Теорема.
b
X ∈ L является наилучшим приближением для X ∈ H тогда и только
тогда, когда
(X −
b
X, Y ) = 0 для любого Y ∈ L,
т. е. X −
b
X ортогонально L и в этом смысле
b
X есть «проекция» X на L.
Доказательство. Пусть
b
X — наилучшее приближение, тогда
kX −
b
Xk = min
Y ∈L
kX − Y k = min
∆∈L
kX −
b
X − ∆k,
где ∆ = Y −
b
X. Зафиксируем некоторое ∆
0
6= 0 из L и рассмотрим минимум по
выделенному направлению:
min
λ
kX −
b
X − λ∆
0
k
2
= min
λ
(X −
b
X − λ∆
0
, X −
b
X − λ∆
0
) = min
λ
(A
2
− 2λB + λ
2
C
2
),
70
