Лотов В.И. Теория вероятностей. Конспект лекций

Подождите немного. Документ загружается.

Из условия теоремы следует, что d

< 1 при всех i, j, поэтому d = max

i,j

< 1.

Таким образом, мы приходим к неравенству: для всякого n ≥ 1

(n + n

) −m

(n + n

) ≤ d(M

(n) −m

(n)).

Теперь будем устремлять n к бесконечности. Каждое число n можно представить в

виде n = sn

+ u, здесь s = [n/n

], 0 ≤ u < n

, и s → ∞, если n → ∞. Поэтому

0 ≤ M

(n) −m

(n) ≤ M

(sn

) −m

(sn

) ≤ d(M

((s −1)n

) −m

((s −1)n

)) ≤

≤ . . . ≤ d

s−1

) −m

)) ≤ d

s−1

→ 0

при n → ∞.

Напомним, что m

(n) ≤ p

(n) ≤ M

(n), значит, при всех i вероятности p

(n)

сходятся к одному и тому же пределу p

при n → ∞.

Далее, переходя в равенстве

(n + 1) =

k=1

(n)p

к пределу при n → ∞, получим

k=1

Кроме того,

j=1

(n) = 1. Переходя к пределу при n → ∞ получаем

j=1

= 1.

Нам осталось доказать, что числа {p

, . . . , p

} являются единственным решени-

ем указанной системы уравнений. Предположим, что нашелся другой вектор x =

, . . . , x

), для которого

= 1 и x

k=1

, j = 1, . . . , r. Последнее озна-

чает, что x = xP = xP

= . . . = xP

для любого n ≥ 1. В покоординатной записи это

выглядит так:

k=1

(n).

Переходя в этом равенстве к пределу при n → ∞, получим

k=1

= p

Теорема доказана.

Если задана матрица P вероятностей перехода, то для проверки условия теоре-

мы нужно искать показатель степени n

, при котором все элементы матрицы P

отличны от нуля. Возведение матрицы в степень является весьма трудоемкой опера-

цией. Ее можно избежать, если воспользоваться простой графической иллюстрацией.

По матрице P можно построить диаграмму, в которой состояния изображаются от-

дельными точками, а наличие положительной вероятности перехода из состояния в

состояние показывается стрелочкой. Пусть, к примеру, r = 4,

P =







1/2 1/2 0 0

0 0 1 0

1/3 0 1/3 1/3

0 0 1 0







Построим диаграмму.

101

d d

Нетрудно видеть, что из каждого состояния за 3 шага можно с положительной ве-

роятностью перейти в любое из четырех состояний, то есть условие теоремы выпол-

няется для n

= 3.

6. Ветвящиеся процессы

Рассмотрим несколько примеров ветвящихся процессов.

1. Цепная реакция. Пусть имеется частица, которая в определенный момент вре-

мени распадается на некоторое случайное число новых частиц, каждая из которых,

в свою очередь, ведет себя так же.

2. Распространение эпидемии. Больной заражает некоторое случайное число дру-

гих людей, каждый из которых также является источником инфекции и заражает

других людей.

3. Развитие биологической популяции, состоящей, к примеру, из одноклеточных,

которые размножаются по определенному закону.

В этом разделе мы рассмотрим одну из простейших математических моделей

ветвящихся процессов.

Предположим, что в момент времени n = 0 имеется всего одна частица (отне-

сем ее к нулевому поколению), которая в некоторый момент времени в результате

акта деления переходит в k частиц того же типа с вероятностью p

, k = 0, 1, . . .,

∞

k=0

= 1. Полученные частицы образуют первое поколение. Каждая из частиц

этого поколения ведет себя точно так же, независимо от предыстории и судьбы дру-

гих частиц. В результате мы получаем второе поколение, и т.д.

b b b b

b b b b b b b b b

n = 0

n = 1

n = 2



Будем считать для простоты, что каждая частица живет единицу времени. Обозна-

чим Y

число частиц в n-м поколении, n = 0, 1, . . ., Y

= 1.

Пусть имеются независимые последовательности независимых случайных вели-

чин {X

(1)

}, {X

(2)

}, . . ., n ≥ 1, где при всех j и n

P(X

(j)

= k) = p

, k = 0, 1, . . . .

Смысл их введения состоит в следующем: случайные величины X

(j)

, X

(j)

, . . . равны

числу потомков частиц из (j −1)-го поколения, эти потомки формируют j-е поколе-

102

ние. Последовательность Y

можно представить в виде

= 1,

= X

(1)

= X

(2)

+ . . . + X

(2)

. . . . . . . . . . . . . . . . . .

= X

(n)

+ . . . + X

(n)

n−1

Таким образом, мы построили модель простейшего ветвящегося случайного процесса

(в литературе такие модели получили название процессов Гальтона-Ватсона). После-

довательность Y

является цепью Маркова, однако матрица переходных вероятно-

стей для нее трудна для вычислений, поэтому для исследования ветвящихся процес-

сов разработаны свои собственные методы. Обычно интересуются распределением

числа частиц в n-м поколении, его предельным поведением при n → ∞, вероятно-

стью вырождения процесса в какой-то момент времени.

Весьма удобным инструментом исследования ветвящихся процессов являются

производящие функции.

Пусть

g(z) = E z

(1)

∞

k=0

P(X

(1)

= k), |z| ≤ 1,

— производящая функция потомства одной частицы (не важно, какой именно; слу-

чайные величины X

(j)

одинаково распределены) и пусть g

(z) означает n-ю итерацию

функции g(z), то есть

(z) = g(z), g

(z) = g(g(z)), . . . ,

(z) = g(g

n−1

(z)) = g

n−1

(g(z)).

Следующая теорема устанавливает вид производящей функции числа частиц в

n-м поколении.

Теорема. Для любого n ≥ 1

E z

∞

k=0

P(Y

= k) = g

(z).

Доказательство. Воспользуемся методом математической индукции. При n = 1

имеем E z

= g(z) = g

(z). Предположим, что E z

n−1

= g

n−1

(z). Тогда

∞

k=0

P(Y

= k) =

∞

k=0

∞

m=0

P(Y

= k, Y

n−1

= m) =

∞

k=0

∞

m=0

P(X

(n)

+ . . . + X

(n)

= k, Y

n−1

= m) =

∞

k=0

∞

m=0

P(X

(n)

+ . . . + X

(n)

= k)P(Y

n−1

= m) =

∞

m=0

P(Y

n−1

= m)

∞

k=0

P(X

(n)

+ . . . + X

(n)

= k) =

103

∞

m=0

(n)

+...+X

(n)

P(Y

n−1

= m) =

∞

m=0

(n)

···z

(n)

P(Y

n−1

= m) =

∞

m=0

(n)

···Ez

(n)

P(Y

n−1

= m) =

∞

m=0

(z)P(Y

n−1

= m) = g

n−1

(g(z)) = g

(z).

Теорема доказана.

Знание производящей функции g

(z) позволяет найти все коэффициенты при z

(например, P(Y

= 0) = g

(0), P(Y

= 1) = g

(0), P(Y

= 2) = g

(0)/2 и т.д.), а также

изучать свойства этих вероятностей.

Мы рассмотрим далее вопрос о вероятности вырождения процесса.

Процесс вырождается, если Y

= 0 при некотором n. Обозначим A

событие,

состоящее в том, что Y

= 0. Тогда вырождению процесса будет соответствовать

событие

A =

∞

[

n=1

= 0} =

∞

[

n=1

Обозначим через r = P(A) вероятность вырождения.

Теорема. Вероятность вырождения r равна наименьшему корню уравнения

z = g(z) (11)

на отрезке [0, 1].

Доказательство.

Очевидно, A

⊂ A

⊂ . . ., поэтому по свойству непрерывности вероятности

r = P(A) = lim

n→∞

P(A

) = lim

n→∞

(0).

Устремим n к бесконечности в равенстве

n+1

(0) = g(g

(0)),

тогда пределом левой части будет число r, а правая часть стремится к g(r) в си-

лу непрерывности функции g(z), то есть действительно вероятность вырождения

удовлетворяет соотношению r = g(r). Однако у уравнения (11) могут быть и дру-

гие корни, поэтому осталось доказать, что r совпадает с наименьшим корнем этого

уравнения на [0,1].

Тривиальный случай: если P(X

(1)

= 1) = 1, то Y

= 1 при всех n, то есть вы-

рождения не происходит и, естественно, r = 0. Поскольку в этом случае g(z) ≡ z, то

уравнение (11) превращается в тождество z = z, наименьшим решением которого на

[0,1] является нуль.

Пусть теперь P(X

(1)

= 1) < 1. Выясним, как выглядит график функции g(z) на

[0,1]. Функция является выпуклой вниз, поскольку g

(z) =

k(k −1)z

k−2

≥ 0. Кроме

того, g(1) = 1. Обозначим a = E X

(1)

и заметим, что a =

k P(X

(1)

= k) = g

(1).

Рассмотрим два случая.

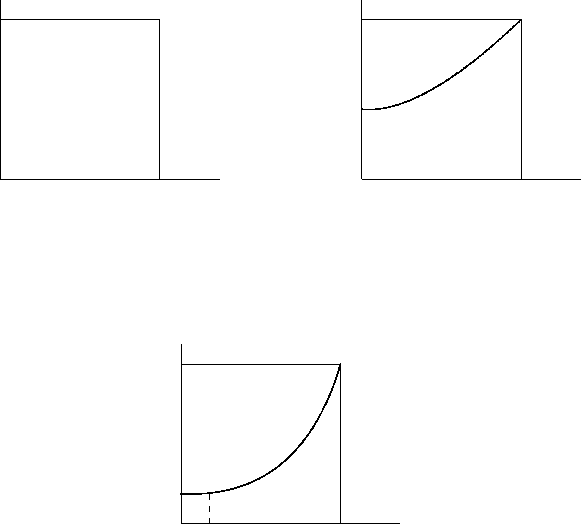
1) Предположим, что a ≤ 1. Если P(X

(1)

> 1) = 0, то графиком функции g(z)

будет прямая g(z) = P(X

(1)

= 0) + zP(X

(1)

= 1) (Рис. 1а), причем P(X

(1)

= 0) > 0.

Поскольку g(1) = 1 и g

(1) < 1, то единственным решением уравнения (11) на [0,1]

будет число z = 1, то есть в этом случае r = 1. Если же P(X

(1)

> 1) > 0, то кривая

y = g(z) также будет пересекать прямую y = z только при z = 1 (Рис. 1б), то есть и

в этом случае r = 1.

104

0 1 z

y = g(z)

Рис. 1а

0 1

y = g(z)

Рис. 1б

2) Пусть теперь a > 1. Тогда, разумеется, P(X

(1)

> 1) > 0, и уравнение (11) имеет

ровно два корня r

< 1 и r

= 1 (См. Рис. 2).

0 1

y = g(z)

Рис. 2

Предположим, что r = r

= 1. Тогда δ

= 1 − g

(0) → 1 − r = 0 при n → ∞ и,

следовательно, g(1 − δ

) < 1 − δ

при достаточно больших n. В этом случае

n+1

= 1 −g

n+1

(0) = 1 − g(g

(0)) = 1 − g(1 − δ

) > 1 − (1 − δ

) = δ

что противоречит сходимости δ

→ 0. Значит, r = r

. Теорема доказана.

Итак, мы видим, что возможность вырождения процесса определяется значением

среднего числа потомков одной частицы. Если исключить из рассмотрения упомяну-

тый выше тривиальный случай, то при a ≤ 1 процесс вырождается с вероятностью

единица, а при a > 1 вероятность вырождения меньше единицы (она обращается в

нуль при g(0) = 0 = P(X

(1)

= 0)).

Ветвящийся процесс принято называть докритическим, если a < 1, критическим

при a = 1, и надкритическим, если a > 1.

7. Случайные процессы с непрерывным временем

7.1. Общие определения

До сих пор мы рассматривали семейства случайных величин, у которых множе-

ство индексов конечно или счетно, то есть мы рассматривали последовательности

случайных величин {X

, n ≥ 1}. Во многих случаях значения индекса n интерпре-

тировались как дискретные моменты времени.

Определение. Случайным процессом называется произвольное семейство слу-

чайных величин {X

, t ∈ T ⊂ R}, заданных на одном вероятностном пространстве.

В отличие от последовательностей случайных величин при рассмотрении случай-

ных процессов чаще всего предполагают, что T = [a, b] или T = [0, ∞). Параметр t

интерпретируется как время.

105

Отметим, что при фиксированном t мы имеем случайную величину X

(ω), а при

фиксированном ω получаем функцию {X

, t ∈ T }, называемую обычно траекторией

процесса.

Если зафиксируем t

, . . . , t

— некоторые значения параметра t, то им будет соот-

ветствовать случайный вектор (X

, X

, . . . , X

). Распределения всевозможных та-

ких векторов, когда t

∈ T, . . . , t

∈ T , называются конечномерными распределения-

ми процесса.

Предположим, что X

(ω) = 0.

Определение. Случайный процесс {X

, t ≥ 0} называется процессом с незави-

симыми приращениями, если для любых 0 ≤ t

< t

< . . . < t

случайные величины

, X

− X

, . . . , X

− X

n−1

независимы.

Определение. Случайный процесс с независимыми приращениями называется

однородным, если при любых t

< t

распределение X

− X

определяется только

длиной интервала t

− t

и не зависит от t

Ниже мы рассмотрим один из наиболее простых и в то же время достаточно

важных для приложений процессов с независимыми приращениями — пуассоновский.

7.2. Процесс Пуассона

Предположим, что в случайные моменты времени одно за другим происходят

некоторые события. Нас интересует число таких событий, произошедших в проме-

жутке времени [0, t]. Обозначим X

это число.

Примерами таких ситуаций могут быть число частиц, зафиксированных прибо-

ром, число станков, вышедших из строя, число судов, прибывших в порт и т.д.

Относительно процесса появления событий будем предполагать следующее.

I. X

— однородный процесс с независимыми приращениями.

Это означает, во-первых, что вероятность появления k событий в любом проме-

жутке времени [τ, τ + t] зависит только от t и не зависит от τ; во-вторых, это все

происходит вне зависимости от того, сколько событий и как появлялись до момен-

та τ.

II. Обозначим P

(t) = P(X

= k), k = 0, 1, . . ., и будем предполагать, что при

h → 0

P(X

≥ 2) =

∞

k=2

(h) = o(h).

Это условие означает практическую невозможность появления двух или более собы-

тий за малый промежуток времени h.

Наша задача — найти в этих условиях вероятности P

(t). Мы покажем, что за

исключением некоторых тривиальных случаев имеет место

(t) =

(λt)

k !

−λt

, k = 0, 1, . . . ,

при некотором λ > 0.

Наши действия разобьем на несколько этапов.

1. Покажем, что за исключением некоторых простых ситуаций при некотором

λ > 0 выполняется P

(t) = e

−λt

Действительно, пусть p = P

(1). Разобьем отрезок времени [0,1] на n равных ча-

стей; отсутствие событий за единицу времени означает, что на каждом из маленьких

106

промежутков времени длины 1/n происходит 0 событий. В силу независимости полу-

чаем p = (P

(1/n))

, откуда P

(1/n) = p

1/n

. Отсюда сразу же следует P

(k/n) = p

k/n

при любом k ≥ 1.

Покажем теперь, что вообще P

(t) = p

при всех t ≥ 0. Для каждого такого числа

t и произвольного натурального n найдется число k ≥ 1 такое, что

k − 1

≤ t <

Функция P

(t) не возрастает по t, поэтому

k − 1

≥ P

(t) ≥ P

или

k−1

≥ P

(t) ≥ p

Устремив n → ∞ так, что k/n → t, получим P

(t) = p

Возможны три случая: а) p = 0, б) p = 1, и в) 0 < p < 1.

В первом из них P

(t) = 0 для любого t > 0, то есть с вероятностью 1 в любом как

угодно малом промежутке времени происходит хотя бы одно событие, а это эквива-

лентно тому, что в промежутке времени любой длины происходит бесконечно много

событий. Это можно представлять себе как цепную реакцию при атомном взрыве,

мы не будем останавливаться на этой крайности. В случае б) P

(t) = 1, то есть со-

бытия никогда не появляются. Таким образом, интерес вызывает только случай в).

Положим p = e

−λ

, здесь 0 < λ < ∞. Тем самым получили

(t) = e

−λt

2. Покажем, что при h → 0

(h) = λh + o(h).

Для этого воспользуемся тем, что P

(h) = e

−λh

= 1 − λh + o(h), и

(h) + P

(h) +

∞

k=2

(h) = 1.

Отсюда

(h) = 1 − P

(h) −

∞

k=2

(h) = λh + o(h).

3. В этом пункте мы покажем, что вероятности P

(t) удовлетворяют некоторой

системе дифференциальных уравнений.

Для t ≥ 0 и h > 0 имеем

(t + h) =

j=0

(t)P

k−j

(h)

(мы перебираем здесь все возможности о том, сколько событий произошло за время

t и за последующий промежуток времени длины h).

Если h → 0, то

k−2

j=0

(t)P

k−j

(h) ≤

k−2

j=0

k−j

(h) =

i=2

(h) = o(h),

107

поэтому при k ≥ 1

(t + h) = P

(t)P

(h) + P

k−1

(t)P

(h) + o(h) =

= P

(t)(1 −λh + o(h)) + P

k−1

(t)(λh + o(h)) + o(h) =

= P

(t)(1 −λh) + P

k−1

(t)λh + o(h).

Отсюда получаем

(t + h) −P

(t)

= −λP

(t) + λP

k−1

(t) +

o(h)

, k = 1, 2, . . . .

Устремим h → 0. Поскольку при этом предел правой части существует, то он

будет существовать и для левой части. В результате получаем

(t) = −λP

(t) + λP

k−1

(t), k = 1, 2, . . . .

К этой системе можно добавить соотношение

(t) = −λP

(t),

которое следует из формулы P

(t) = e

−λt

. Выберем начальные условия — они дикту-

ются логикой здравого смысла:

(0) = 1, P

(0) = 0 при k ≥ 1.

4. Решение системы уравнений.

Воспользуемся методом производящих функций. Обозначим

g(z, t) =

∞

k=0

(t), |z| ≤ 1. (12)

Умножим полученные нами уравнения для P

(t) на z

и просуммируем по k:

∞

k=0

(t) = −λ

∞

k=0

(t) + λ

∞

k=1

k−1

(t),

или, что то же самое,

∂g(z, t)

∂t

= −λg(z, t) + λzg(z, t) = λ(z − 1)g(z, t).

Перепишем полученное уравнение в виде

∂ ln g(z, t)

∂t

= λ(z − 1),

откуда

ln g(z, t) = λ(z − 1)t + C.

В силу выбранных начальных условий при t = 0 имеем g(z, 0) = 1, то есть C = 0. В

итоге получаем

g(z, t) = e

λ(z−1)t

= e

−λt

λzt

= e

−λt

∞

k=0

(λt)

k !

. (13)

108

Сравнивая коэффициенты разложений (12) и (13), обнаруживаем, что

(t) =

(λt)

k !

−λt

, k = 0, 1, . . . ,

то есть мы получили вероятности, соответствующие распределению Пуассона с пара-

метром λt. По этой причине изучаемый процесс называется пуассоновским. Иногда

говорят о пуассоновском потоке событий.

Обозначим через τ

длину промежутка времени от нуля до первого появления со-

бытия. Очевидно, P(τ

> t) = P

(t) = e

−λt

, то есть случайная величина τ

распреде-

лена по показательному закону с параметром λ. Пусть также τ

— длина промежутка

времени между первым и вторым событиями, τ

— длина промежутка времени меж-

ду вторым и третьим событиями, и так далее. Можно показать, что все случайные

величины τ

, τ

, . . . независимы и одинаково распределены по показательному закону

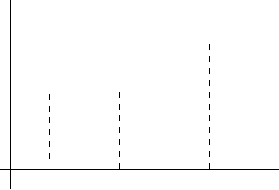
с параметром λ. Траектории процесса X

выглядят следующим образом.

Здесь обозначено v

= τ

+ . . . + τ

. Момент v

k-го появления события равен сумме

независимых случайных величин, имеющих показательное распределение с парамет-

ром λ, поэтому v

⊂= Γ

λ,k

(t) =











(k − 1)!

k−1

−λt

, t > 0,

0, иначе.

Этот частный случай гамма-распределения принято называть распределением Эрл´анга.

Нетрудно вычислить среднее число событий, происходящих за время t:

E X

∞

k=0

k P

(t) = λt.

Среднее число событий, происходящих за единицу времени, называется интенсив-

ностью пуассоновского процесса; мы видим, что она совпадает с параметром λ рас-

пределения промежутка времени между двумя последовательными событиями.

Вернемся к анализу траекторий процесса Пуассона. Они являются кусочно посто-

янными. При возрастании t величина X

остается постоянной в течение промежутка

времени, имеющего показательное распределение, а затем скачком увеличивается на

единицу. Можно рассмотреть более общую конструкцию, когда X

в момент времени

t = v

увеличивается на случайную величину Y

, в момент времени v

происходит

скачок на величину Y

и так далее, где Y

, Y

, . . . — последовательность независимых

одинаково распределенных случайных величин, не зависящая также от последова-

тельности τ

, τ

, . . .. Полученный таким образом случайный процесс Z

называется

обобщенным процессом Пуассона. Разумеется, его изучать труднее, чем обычный

109

процесс Пуассона, и мы не будем этого делать. Отметим только, что если к постро-

енному процессу добавить еще линейный снос (то есть рассмотреть процесс вида

= u + vt + Z

), то получится процесс, имеющий многочисленные приложения в

теории страхования.

Рассмотрим более подробно эту модель.

Предположим, что страховая компания начинает в момент времени t = 0 свою де-

ятельность, имея стартовый капитал u. Доход компании формируется из страховых

взносов. Мы будем считать их постоянными во времени, то есть за время t суммарные

поступления взносов составляют величину vt при некотором v > 0 . Через случайные

промежутки времени τ

, τ

, . . . происходят некоторые события, вынуждающие компа-

нию делать страховые выплаты Y

, Y

, . . .; при этом капитал компании скачкообразно

уменьшается.

u ¡

При изучении таких процессов наибольший интерес вызывает нахождение вероят-

ности разорения, то есть вероятности того, что траектория процесса когда-либо кос-

нется оси абсцисс. Эта задача не проста, и ее решение выходит за рамки нашего

курса. Однако исследование таких процессов во многом опирается на установленные

нами свойства процесса Пуассона.

Список использованной литературы

Боровков А.А. Теория вероятностей. М.: Наука, 1986. 431 с.

Гнеденко Б. В. Курс теории вероятностей. М.: Наука, 1988. 448 с.

110