Лінійна алгебра та аналітична геометрія

Подождите немного. Документ загружается.

18. Поверхні 2-го порядку 171

1. Однопорожнинний гіперболоїд не проходить через початок каноні-

чної системи координат, бо координати точки

(0;0;0)

не справджують

рівняння (18.4).

2. Однопорожнинний гіперболоїд перетинає вісь

у вершинах —

точках

1,2

( ;0;0),

A a



а вісь

— у точках

1,2

(0; ;0).

B b



Вісь

однопо-

рожнинний гіперболоїд не перетинає. Відрізки

1 2

A A

та

1 2

B B

називають

дійсними осями однопорожнинного гіперболоїда. Числа

, ,

a b c

називають

півосями однопорожнинного гіперболоїда.

3. Рівняння поверхні містить змінні

, ,

x y z

у парних степенях, тому

однопорожнинний гіперболоїд симетричний щодо всіх координатних пло-

щин, координатних осей і початку координат.

4. З рівняння однопорожнинного гіперболоїда випливає, що

2 2

x y

a b

 

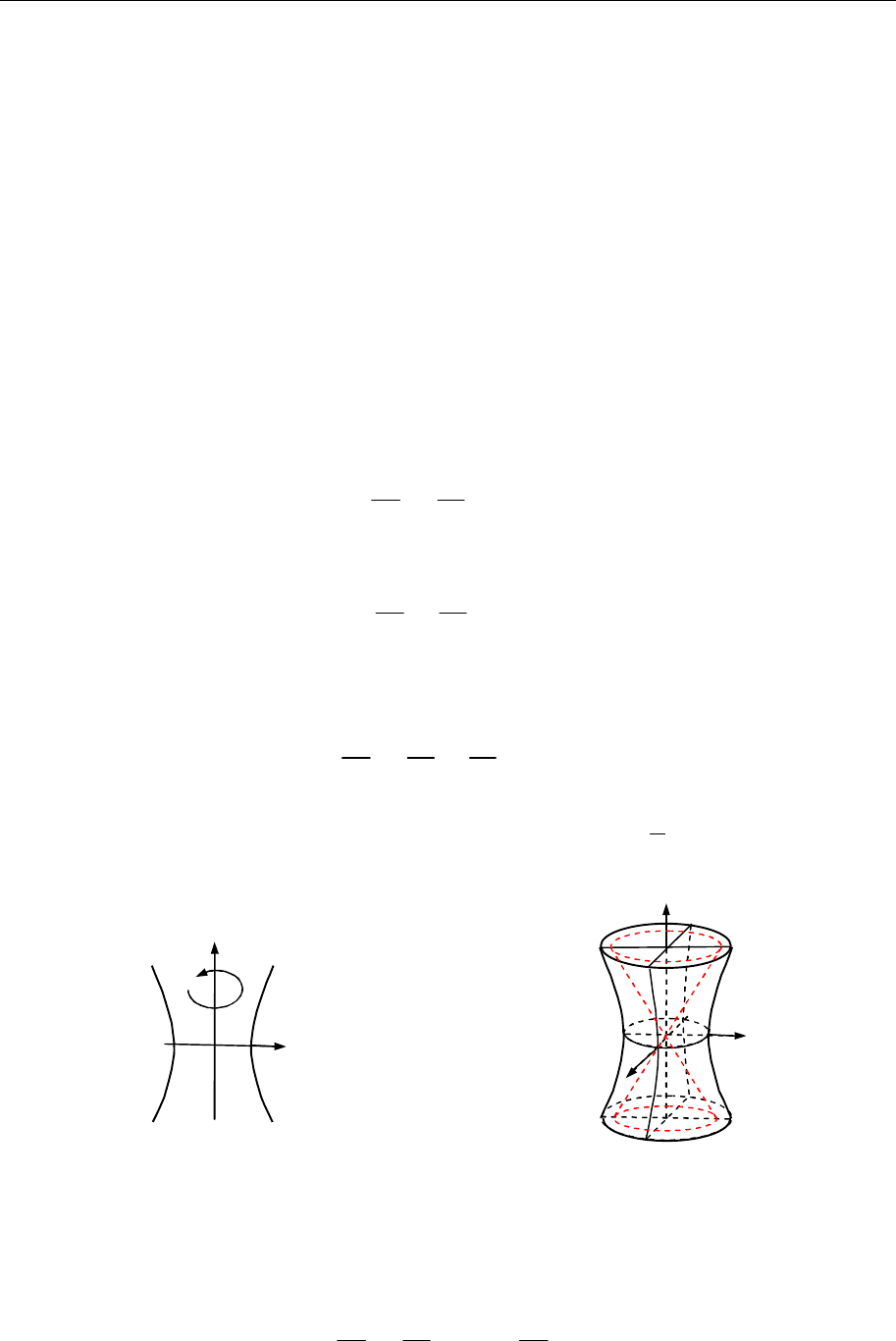
5. Обертанням гіперболи

2 2

y z

a c

 

навколо осі

(рис. 18.19) одержимо однопорожнинний гіперболоїд обер-

тання

2 2 2

x y z

a a c

  

а з нього — стисканням уздовж осі

з коефіцієнтом

— однопорожнин-

ний гіперболоїд загального вигляду (рис. 18.20).

Рис. 18.19

Рис. 18.20

6. Вивчімо форму поверхні однопорожнинного гіперболоїда методом

перерізів. Якщо перетнути поверхню площиною

z h



паралельною

площині

Oxy

то проекція перерізу на площину

Oxy

має рівняння

2 2 2

1 .

x y h

a b c

  

За будь-якого значення

це рівняння еліпса (рис. 18.21) з півосями:

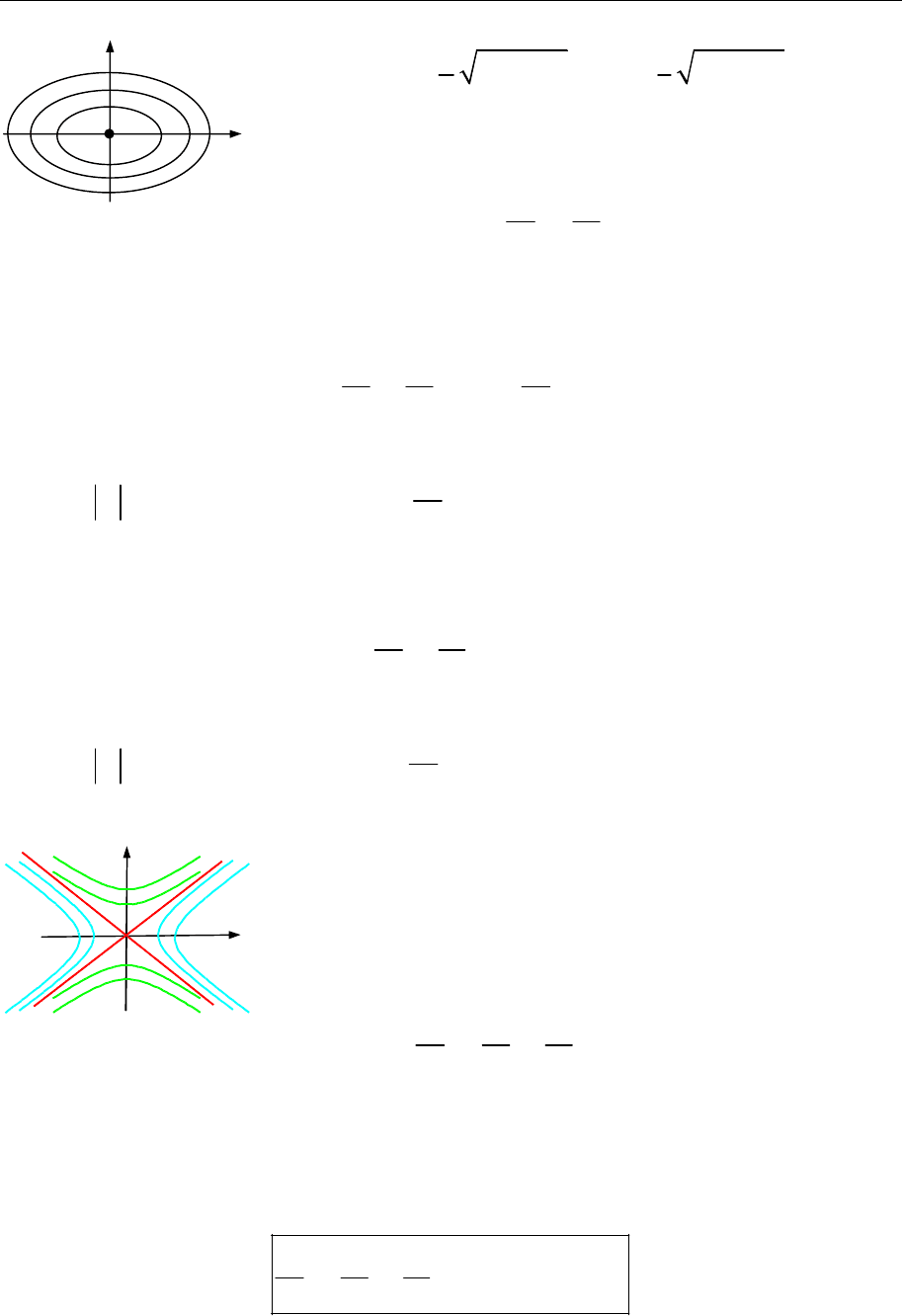
172

Розділ 3. Методи й моделі аналітичної геометрії

Рис. 18.21

2 2 2 2

, .

a b

a c h b c h

c c

 

   

Якщо



матимемо горловий еліпс однопо-

рожнинного гіперболоїда

2 2

x y

a b

 

Якщо поверхню перетнути площиною

x h



яка паралельна площині

Oyz

то проекція перерізу на площину

Oyz

має рівняння

2 2 2

1 .

y z h

b c a

  

Можливі три випадки:

а)

h a



У цьому разі

1 0,

 

тому проекції перерізів на пло-

щину

Oyz

є гіперболами з уявною віссю

(рис. 18.22, І).

б)

h a

 

У цьому разі проекції перерізів збігаються. Їхнє рівняння

2 2

y z

b c

 

означує дві прямі, які перетинаються в початку координат (рис. 18.22, ІІ).

в)

h a



У цьому разі

1 0,

 

тому в перерізі матимемо гіпер-

боли, для яких вісь

є уявною віссю (рис. 18.22, ІІІ).

Рис. 18.22

Те саме матимемо в разі перерізання поверхні

площинами

y h



7. Асимптотичною поверхнею для однопорож-

нинного гіперболоїда є еліптичний конус (однопорож-

нинний гіперболоїд розташований ззовні конуса)

2 2 2

0, , , 0.

x y z

a b c

   

Двопорожнинний гіперболоїд

Двопорожнинним гіперболоїдом називають множину всіх точок простору,

координати яких у деякій ПДСК справджують канонічне рівняння

2 2 2

1, , , 0.

x y z

a b c

    

(18.5)

Систему координат, у якій двопорожнинний гіперболоїд має рівняння

(18.5), називають канонічною системою.

III

18. Поверхні 2-го порядку 173

1. Двопорожнинний гіперболоїд не проходить через початок каноніч-

ної системи координат.

2. Двопорожнинний гіперболоїд перетинає вісь

у двох точках — вер-

шинах —

1,2

(0;0; ).

C c



Осі

та

не перетинають поверхню. Відрізок

1 2

C C

називають дійсною віссю. Числа

a b

та

називають півосями двопоро-

жнинного гіперболоїда.

3. Двопорожнинний гіперболоїд симетричний щодо всіх координат-

них площин, координатних осей і початку координат.

4. Двопорожнинний гіперболоїд міститься всередині асимптотичного

конуса

2 2 2

0, , , 0

x y z

a b c

   

і за межами смуги

z c



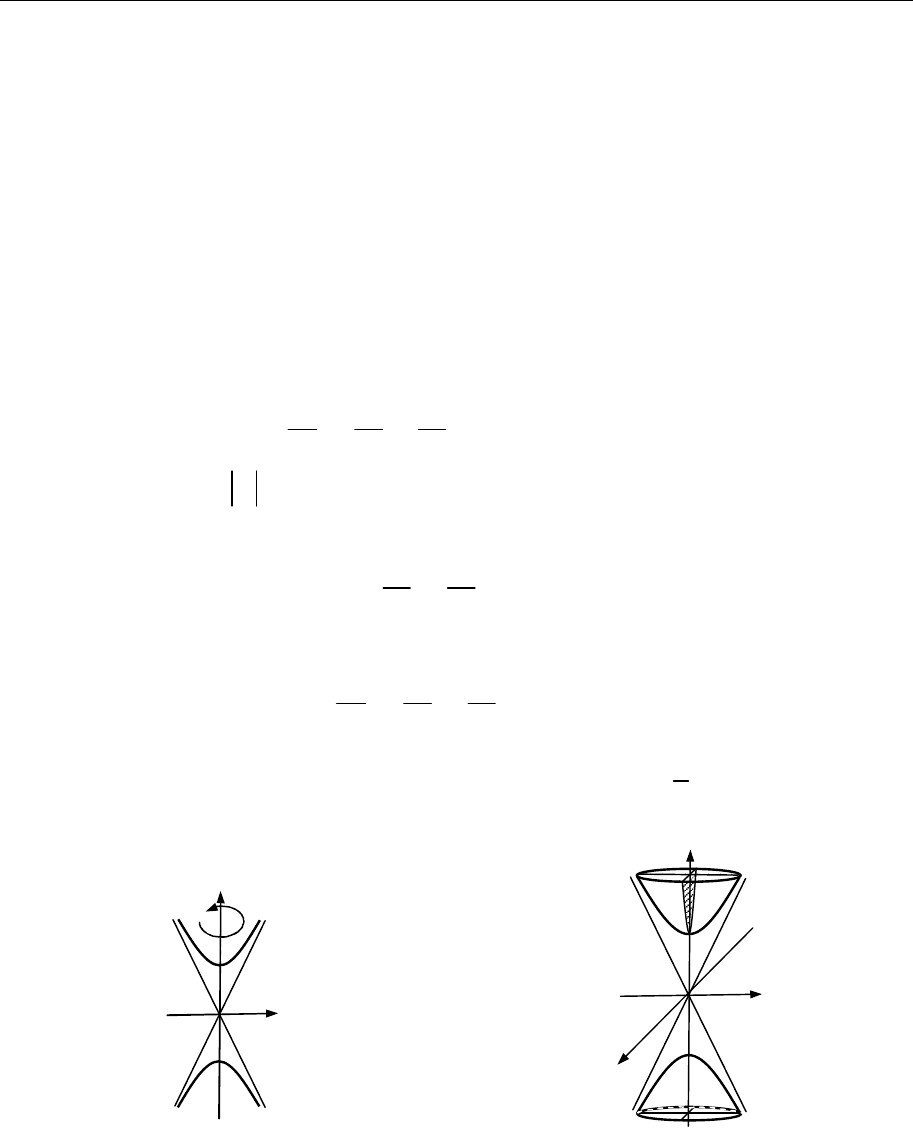
5. Обертанням гіперболи

2 2

z y

c a

 

навколо осі

(рис. 18.23) одержимо двопорожнинний гіперболоїд обертання

2 2 2

x y z

a a c

   

а з нього — стисканням уздовж осі

з коефіцієнтом

— двопорожнин-

ний гіперболоїд загального вигляду (рис. 18.24).

Рис. 18.23

Рис. 18.24

174

Розділ 3. Методи й моделі аналітичної геометрії

18.5. Параболоїди

Еліптичний параболоїд

Еліптичним параболоїдом називають множину всіх точок простору, коор-

динати яких у деякій ПДСК справджують канонічне рівняння

2 2

2 , , 0.

x y

z a b

a b

  

(18.6)

Систему координат, у якій еліптичний параболоїд має рівняння (18.6),

називають канонічною системою.

1. Еліптичний параболоїд проходить через початок ПДСК.

2. Еліптичний параболоїд має з осями координат лише одну спільну

точку — вершину — точку

(0;0;0).

3. Оскільки рівняння (18.6) містить змінні

x y

у парних степенях, то

еліптичний параболоїд симетричний щодо площин

Oxz

та

Oyz

. Поверхня

не симетрична щодо площини

Oxy

Звідси випливає, що еліптичний пара-

болоїд симетричний щодо координатної осі

і не симетричний щодо

осей

та

і початку координат.

4. З рівняння (18.6) випливає, що для всіх точок поверхні



при-

чому



тоді й лише тоді, коли точка збігається з початком координат.

Отже, всі точки еліптичного параболоїда, крім початку координат, розмі-

щені по один бік від площини

Oxy

5. Обертанням параболи

2 2

a z y



навколо осі

(рис. 18.25) одер-

жимо параболоїд обертання

2 2

2 ,

x y





а з нього — стисканням вздовж осі

з коефіцієнтом

— еліптичний

параболоїд загального вигляду (рис. 18.26).

Рис. 18.25

Рис. 18.26

18. Поверхні 2-го порядку 175

Гіперболічний параболоїд

Гіперболічним параболоїдом називають множину всіх точок простору, ко-

ординати яких у деякій ПДСК справджують канонічне рівняння

2 2

2 , , 0.

x y

z a b

a b

  

(18.7)

Систему координат, у якій гіперболічний параболоїд має рівняння

(18.7), називають

канонічною системою.

1. Гіперболічний параболоїд проходить через початок канонічної сис-

теми координат.

2. Гіперболічний параболоїд перетинає осі канонічної системи коор-

динат у єдиній точці — на початку координат.

3. Гіперболічний параболоїд симетричний щодо площин

Oxz

та

Oyz

не симетричний щодо площини

Oxy

Звідси поверхня симетрична щодо осі

і не симетрична щодо осей

та

і початку координат.

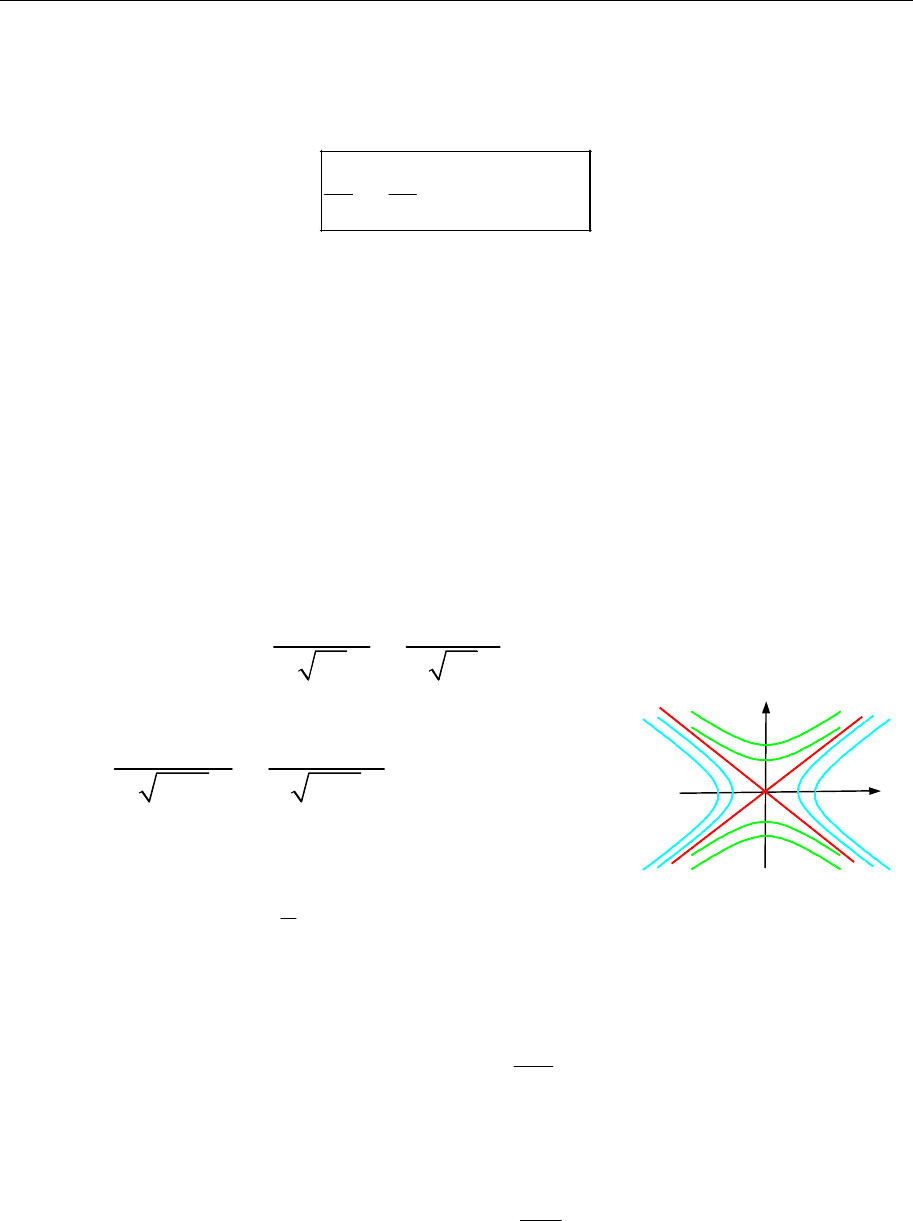
4. Перерізанням поверхні площинами

z h



одержимо гіперболи

(рис. 18.27, І)

2 2

1, 0,

( 2 ) ( 2 )

x y

a h b h

  

спряжені до них гіперболи (рис. 18.27, ІІІ)

2 2

1, 0,

( 2 ) ( 2 )

x y

a h b h

   

 

та пару перетинних прямих — асимптот гіпербол

(рис. 18.27, ІІ)

, 0.

y x h

  

Рис. 18.27

Перерізанням поверхні площинами

y h



одержимо параболи

(рис. 18.28)

2 2

2 .

x a z

 







 











 

Перерізанням поверхні площинами

x h



одержимо параболи

(рис. 18.29).

2 2

2 .

y b z

 







  











 

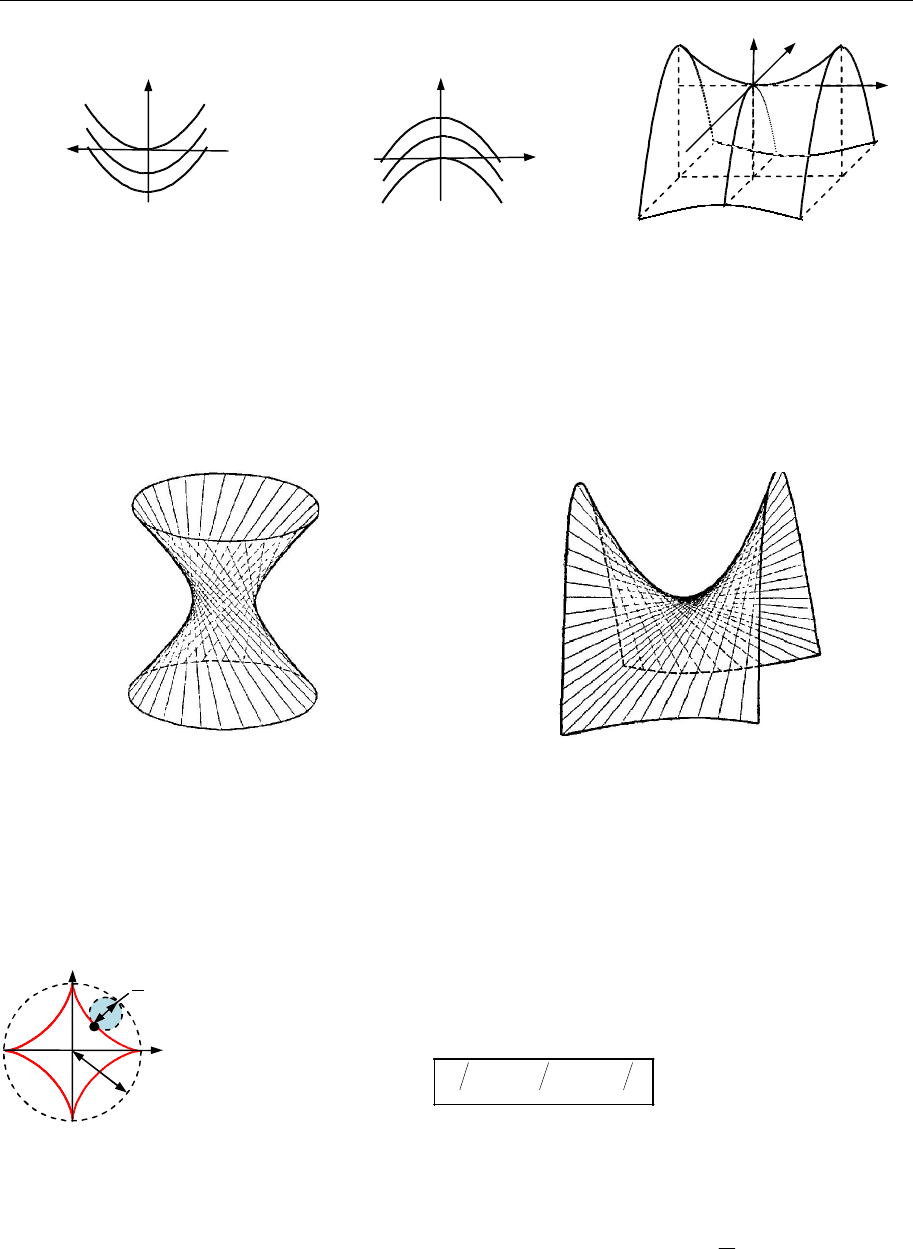
Гіперболічний параболоїд зображено на рис. 18.30.

III

176

Розділ 3. Методи й моделі аналітичної геометрії

Рис. 18.28

Рис. 18.29

Рис. 18.30

Прямолінійні твірні поверхонь 2-го порядку

Деякі з розглянутих поверхонь 2-го порядку можна утворити рухом прямої

лінії. Це очевидно для конуса та циліндра. Виявляється, що однопорож-

нинний гіперболоїд (рис. 18.31) і гіперболічний параболоїд (рис. 18.32) теж

є поверхнями, що утворені прямолінійними твірними.

Рис. 18.31

Рис. 18.32

19. Визначні криві та поверхні

19.1. Плоскі криві у ПДСК

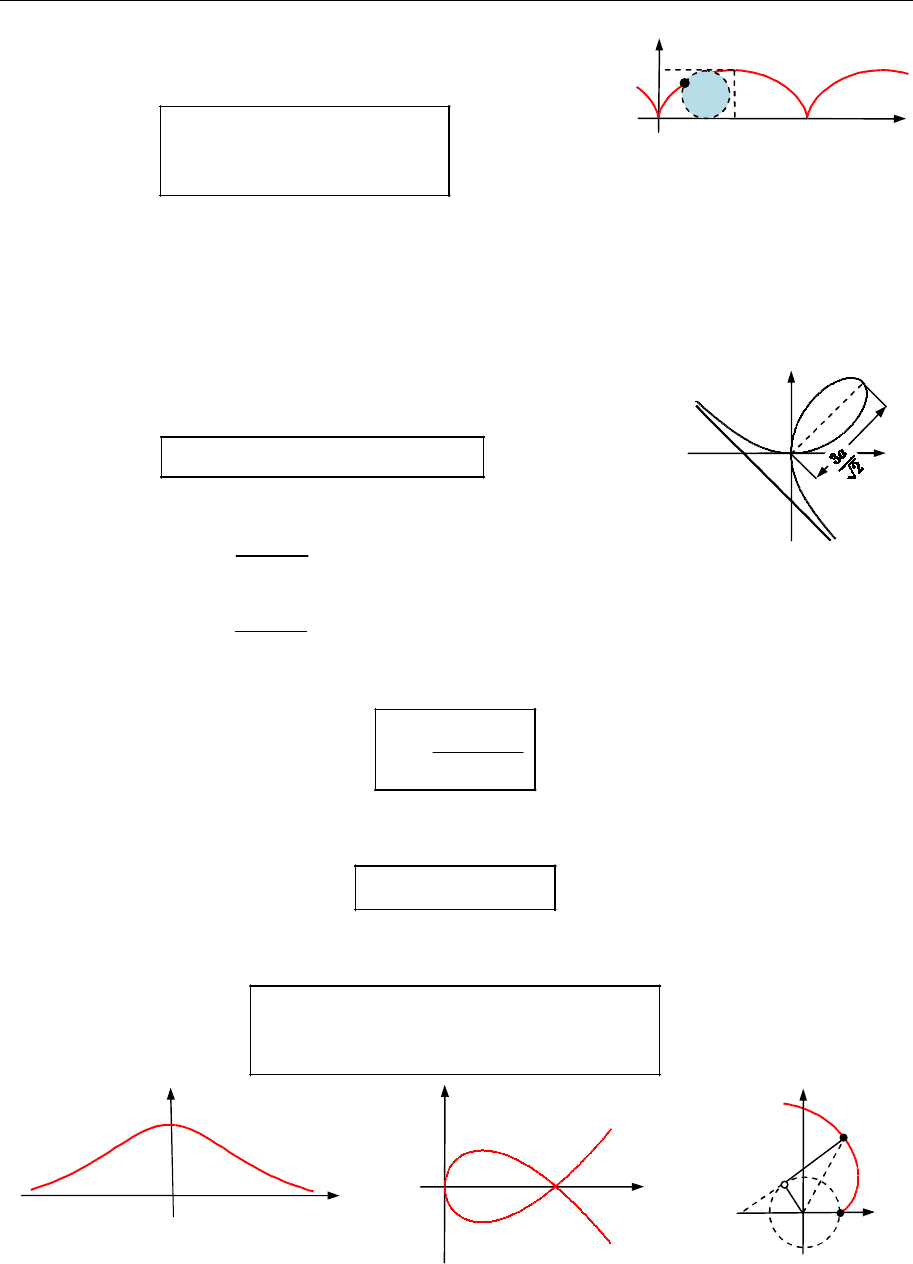
Рис. 19.1

Астроїда (рис. 19.1) — крива , яку задає в деякій

ПДСК:

рівняння

2 3 2 3 2 3

;

x y a 

параметричні рівняння:

cos ,

sin , [0;2 ].

x a t

y a t t













  





Астроїда — траєкторія руху точки

кола радіусом

що котиться

внутрішнім боком кола радіусом



(рис. 19.1).

19. Визначні криві та поверхні 177

Циклоїда (рис. 19.2) — крива, яку в деякій

ПДСК задають параметричні рівняння:

( sin ),

(1 cos ), .

x a t t

y a t t



 







  







Рис. 19.2

Циклоїда — траєкторія руху точки кола, що котиться нерухомою

прямою без ковзання.

Циклоїду утворює нескінченна кількість арок, кожна з яких відповідає

одному обороту кола. Отже, першій арці від початку координат відповідає

змінювання параметра

від

до

2 ;



другій — від



до



тощо.

Декартів листок (рис. 19.3) — крива, яку в

деякій ПДСК задає рівняння

3 3

3 0, 0;

x y axy a   

параметричні рівняння у ПДСК:

, \ { 1}.

y t

















  











Рис. 19.3

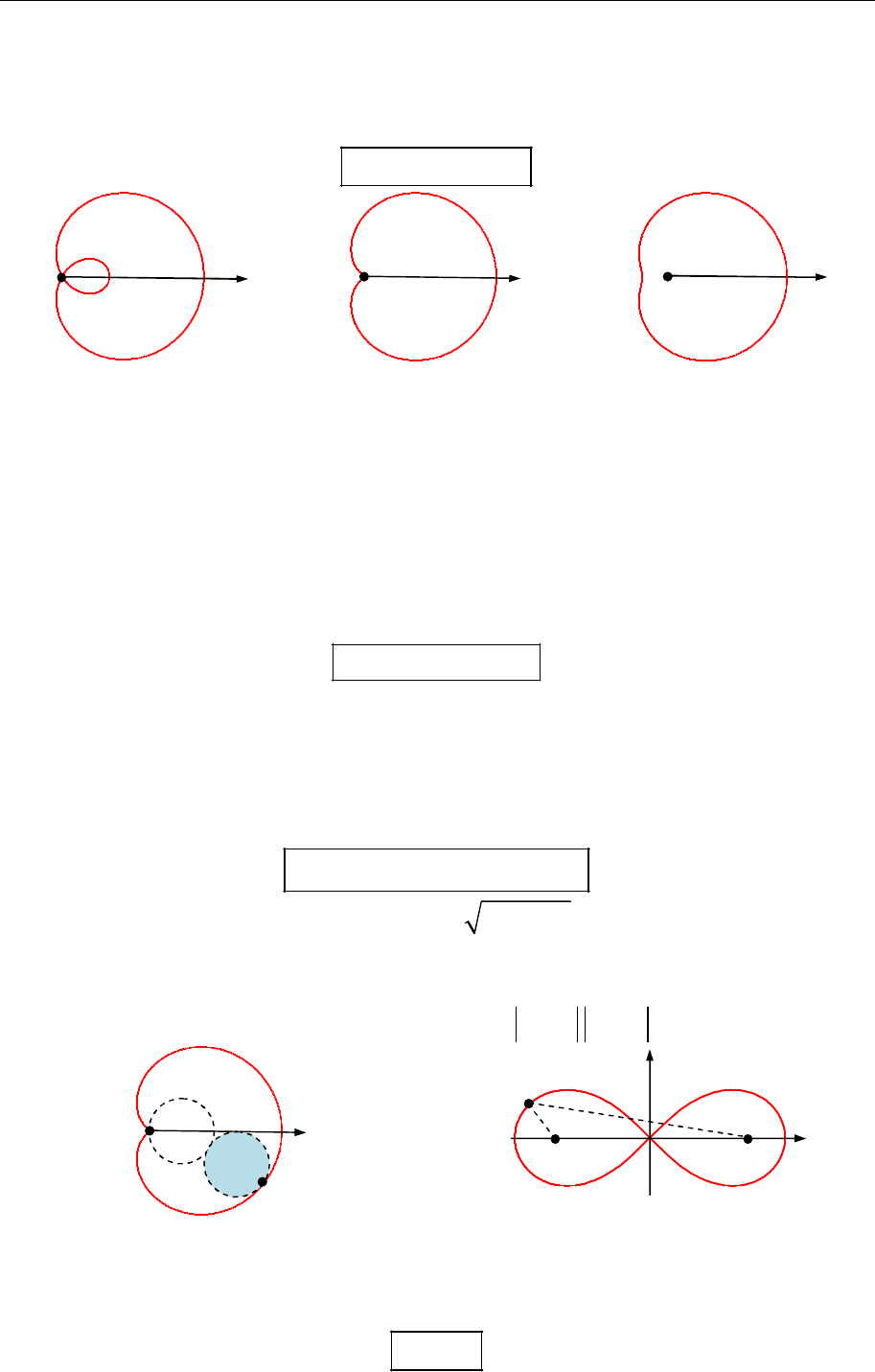
4. Кучер Аньєзі (рис. 19.4) — крива , яку в деякій ПДСК задає рівняння

2 2

x a





5. Петльова парабола (рис. 19.5) — крива, яку в деякій ПДСК задає

рівняння

2 2

( ) .

ay x x a

 

6. Розгортка кола (рис. 19.6) — крива, яку в деякій ПДСК задають па-

раметричні рівняння:

(cos sin ),

(sin cos ), [0; ).

x a t t t

y a t t t t



 







   





Рис. 19.4

Рис. 19.5

Рис. 19.6

x y a

  



178

Розділ 3. Методи й моделі аналітичної геометрії

19.2. Плоскі криві в полярній системі координат

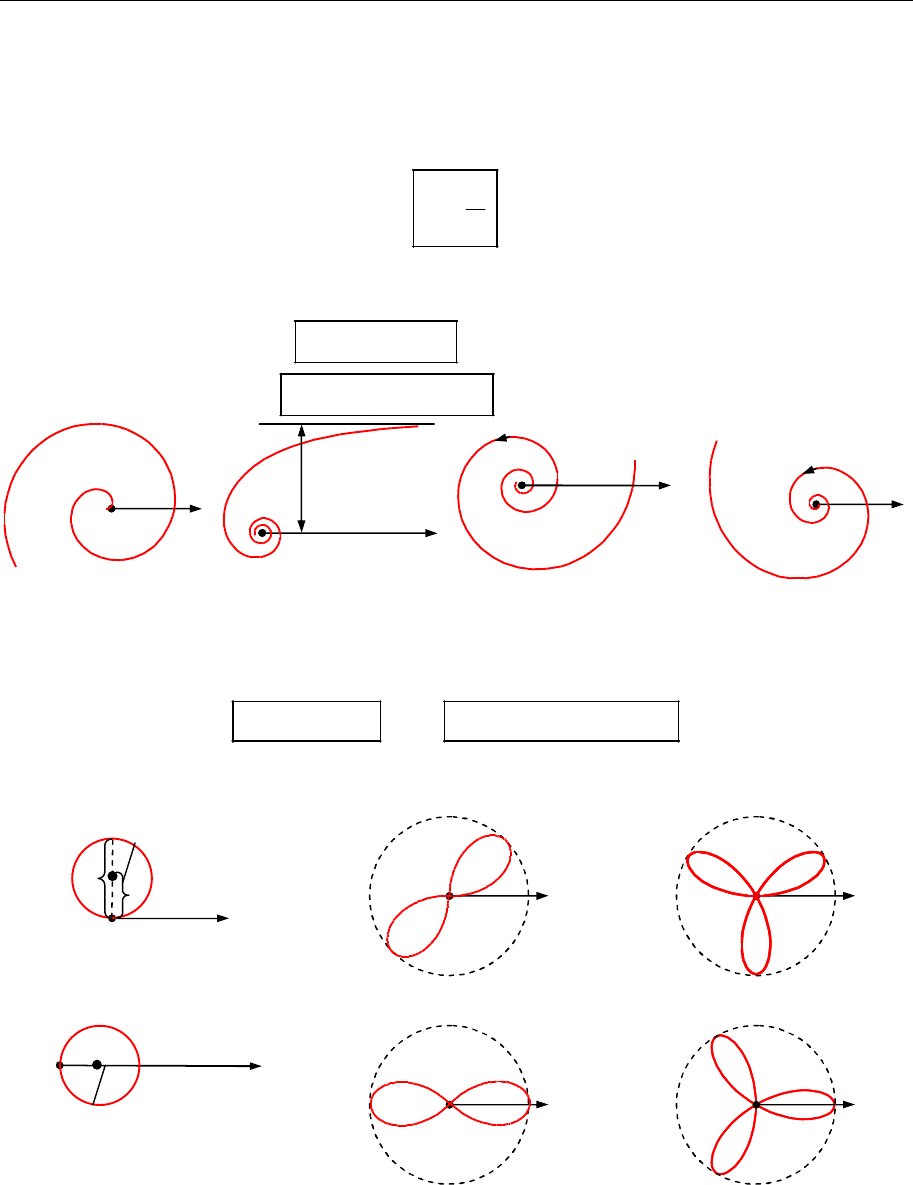
1. Паскалів завиток (рис. 19.7–19.9) — крива, яка має в деякій поляр-

ній системі рівняння

2 cos .

a l

   

Рис. 19.7

Рис. 19.8

Рис. 19.9

Лінія симетрична щодо осі

;

якщо

2 ,

l a



то точка

— вузлова (в

ній лінія перетинає себе), якщо

2 ,

l a



то полюс є точкою вертання, якщо

2 ,

l a



то точка

яка належить кривій, є ізольованою особливою точкою.

Паскалів завиток використовують для креслення профілю ексцентрика,

якщо потрібно, щоб стрижень, який ковзає профілем, коливався гармонічно.

2. Кардіоїда (рис. 19.10) — крива, яку в деякій полярній системі коор-

динат задає рівняння

2 (1 cos ).

   

Кардіоїда — траєкторія руху точки кола радіусом

яке котиться зов-

нішнім боком кола з таким самим радіусом — окремий випадок паскалево-

го завитка.

3. Лемніската Бернуллі (рис. 19.11) — крива, яку в деякій ПДСК задає

рівняння

2 2 2 2 2 2

( ) 2 ( ).

x y a x y

  

Рівняння в полярній системі:

2 cos 2 .

  

Лемніската Бернуллі — множина всіх точок площини, для яких добу-

ток віддалей до двох заданих точок цієї площини є сталим і рівним квадра-

ту половини віддалі між заданими точками:

1 2

F M F M a



(рис. 19.11).

Рис. 19.10

Рис. 19.11

4. Архімедова спіраль (рис. 19.12) — крива , яку в деякій полярній

системі координат задає рівняння

  

19. Визначні криві та поверхні 179

Архімедова спіраль — траєкторія руху точки, що рівномірно рухаєть-

ся прямою, яка рівномірно обертається навколо фіксованої точки.

5. Гіперболічна спіраль (рис. 19.13) — крива, яку в деякій полярній

системі координат задає рівняння

 



6. Логарифмічні спіралі, права і ліва (рис. 19.14 і 19.15) — криві, які в

деякій полярній системі координат задають рівняння

, 1

a a



  

(для правої);

, 0 1

a a



   

(для лівої).

Рис. 19.12

Рис. 19.13

Рис. 19.14

Рис. 19.15

7. Рози (рис. 19.16) — сукупність кривих, які в деякій полярній систе-

мі координат задають рівняннями:

sin

a n

  

або

cos , 0.

a n a   

Рози містяться всередині кола радіусом

;

коли

ціле, то мають

пелюсток.

Рис. 19.16

cos 3

  

cos 2

  

cos

  

sin 3

  

sin 2

  

sin

  

0 1

 



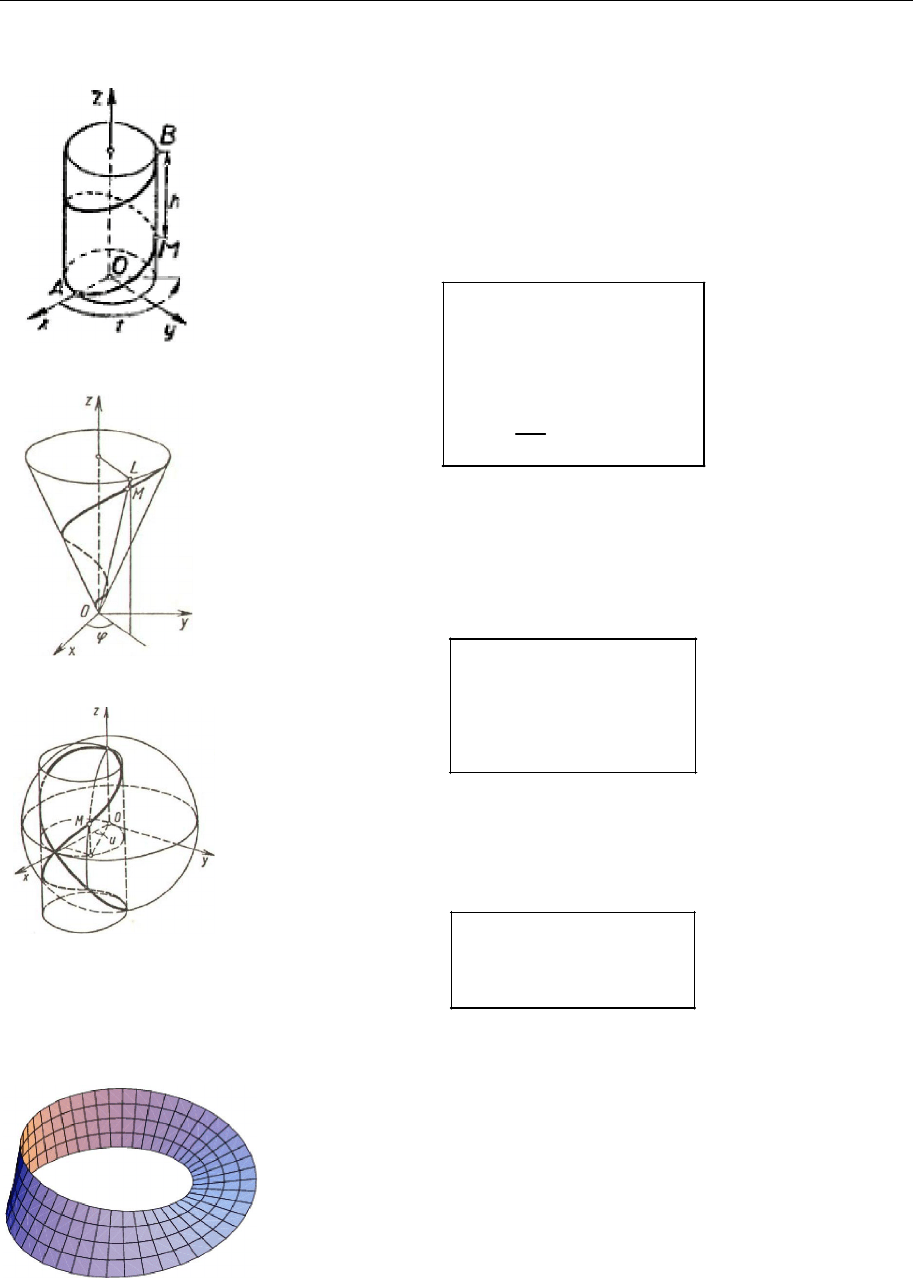
180

Розділ 3. Методи й моделі аналітичної геометрії

19.3. Просторові криві

Рис. 19.17

Рис. 19.18

Рис. 19.19

Циліндрична гвинтова лінія (рис. 19.17) — прос-

торова крива, яку описує точка, що обертається зі ста-

лою кутовою швидкістю навколо нерухомої осі й одно-

часно переміщується поступально зі сталою швидкістю

вздовж цієї осі.

Параметричні рівняння:

cos ,

sin ,

, [0; ),

x a t

y a t

z t















  



 

де

— радіус циліндра;

— крок гвинтової лінії.

Конічна гвинтова лінія (рис. 19.18) — лінія на

поверхні колового конуса, що перетинає всі твірні під

однаковим кутом.

Параметричні рівняння:

cos ,

sin ,

, [0; ).

x at t

y at t

z bt t















  





Крива Вівіані (рис. 19.19) — лінія перетину сфе-

ри з коловим циліндром, удвічі меншого радіуса, ніж

сфера.

Неявні рівняння:

2 2 2 2

2 2

x y z a

x y ax





  







 





19.4. Поверхні

Рис. 19.20

Мебіюсів листок (рис. 19.20) — поверхня,

яку можна одержати склеюванням двох протилеж-

них боків перекрученої прямокутної смужки. Ця

поверхня є прикладом однобічної неорієнтованої

поверхні: якщо рухатись уздовж мебіюсова листка,

не перетинаючи його межі, то (на відміну від двобі-

чних поверхонь, приміром, сфери, циліндра) можна

потрапити в початкову точку, опинившись у пере-

вернутому положенні, тобто з «другого боку».