Литвиненко А.В. Методы и средства защиты информации

Подождите немного. Документ загружается.

Математика разделения секрета 351

Определение 18.3

Матрица V задает БД-совершенную СРС, реализующую структуру доступа Г, если

||V

A∪0

|| = ||V

|| × ||V

δГ (А)

, (18.4)

где δ

(А) = 0, если А ∈ Г, и δ

(А) = 1 в противном случае.

Это определение отличается от определений 1 и 2 тем, что на неразрешенные множе-

ства

А накладываются довольно слабое условие, а именно, если множество строк V с

данными значениями координат из множества

А непусто, то все возможные значения

секрета встречаются в нулевой координате этих строк (без требований “одинаково час-

то” как в комбинаторном определении 2 или же “с априорной вероятностью” как в веро-

ятностном определении 1). Легко видеть, что матрица любой совершенной вероятност-

ной СРС задает БД-совершенную СРС, но обратное неверно.

Для произвольной комбинаторной

СРС, задаваемой матрицей V, определим на мно-

жествах

А ⊆ {0, 1, …, n} функцию h(A) = log

||V

||, где q = |S

|. Легко проверить,

что

max{h(A), h(B)} ≤ h(A ∪ B) ≤ h(A) + h(B) для любых множеств А и В, а условие

(184) может быть переписано в виде

A∪0

) = h

) + δ

(А) h

)

Лемма. Для любой БД-совершенной СРС если А ∉ Г и {A ∪ i} ∈ Г, то h(i) ≥

h(0)

Доказательство. По условиям леммы

h(A ∪ 0) = h(A) + h(0) и h(A ∪ i ∪ 0) = h(A ∪ і). Следовательно,

h(A) + h(i) ≥ h (A ∪ і) = h (A ∪ і ∪ 0) ≥ h(A ∪ 0) = h(A) + h(0)

Так мы предполагаем, что все точки і ∈ {1, …, n} существенные, т.е. для любого і

найдется подмножество

А такое, что А ∉ Г и {A ∪ і} ∈ Г, то из леммы вытекает

Следствие. Для любой БД-совершенной СРС

| ≥ |S

| для всех і = 1, ..., n.

Следствие означает, как отмечалось выше, что для совершенных СРС “размер” про-

екции не может быть меньше “размера” секрета. Поэтому БД-совершенная СРС называ-

ется идеальной, если

| = |S

| для всех і = 1, ..., n.

Замечание. Неравенство

| ≥ |S

| справедливо и для совершенных вероятностных

СРС, поскольку их матрицы задают БД-совершенные СРС.

Естественный вопрос состоит в том, для каких структур доступа Г существуют реа-

лизующие их идеальные (вероятностные или комбинаторные) СРС. Как уже отмеча-

лось, наилучший на сегодняшний день ответ использует слово матроид. Напомним

определение матроидов и некоторые их

основные свойства.

Матроидом называется конечное множество

Х и семейство I его подмножеств, на-

зываемых независимыми (остальные множества называются зависимыми), если выпол-

нены следующие свойства:

352 Глава 18. Криптографическая защита

∅ ∈ I; (18.5.1)

Если A ∈ I и B ⊂ A, то B ∈ I; (18.5.2)

Если A, B ∈ I и |A| = |B| + 1,

то существует a ∈A\B такое, что a ∪ B ∈ I. (18.5.3)

Пример 18.4. Множество Х — это множество векторов в некотором линейном век-

торном пространстве, а независимые подмножества — это линейно независимые под-

множества векторов.

Собственно с этого примера и началась теория матроидов, вначале как попытка дать

аксиоматическое определение линейной независимости векторов через “внутренние

свойства”, т.е. не апеллируя к понятию вектора. К счастью, попытка не удалась,

так как

нашлись матроиды, не представимые как линейные (т.е. как системы векторов), а сама

теория матроидов разрослась далеко за пределы линейной алгебры.

Пример 18.5. (матроид Вамоса). Рассмотрим следующее множество:

Х = {1, 2, 3, 4,

5, 6, 7, 8}

и положим a = {1, 2}, b = {3, 4}, c = {5, 6} и d = {7, 8}. Матроид Вамоса оп-

ределяется как матроид, в котором множества

a ∪ c, a ∪ d, b ∪ c, b ∪ d, c ∪ d, а так-

же все подмножества из пяти или более элементов являются зависимыми. Известно, что

этот матроид не является линейным.

Матроид также можно определить через так называемую ранговую функцию

r(A) мат-

роида, определяемую как максимальная мощность независимого подмножества

В ⊆ А. Оче-

видно, что независимые множества (и только они) задаются условием

r(A) = |A|. Ранговая

функция матроида обладает свойствами

r(A) ∈Z; r(∅) = 0; (18.6.1)

r(A) ≤ r(A ∪ b) ≤ r(A) + 1; (18.6.2)

Если r(A ∪ b) = r (A ∪ c) = r(A), то r (A ∪ b ∪ c) = r(A). (18.6.3)

Обратно, пусть некоторая функция r(A) обладает свойствами (18.6). Назовем незави-

симыми те множества

А, для которых r(A) = |A|. Тогда эти множества задают матроид,

а функция

r является его ранговой функцией. Возможно также определить матроид че-

рез минимальные зависимые множества, называемые циклами. Матроид называется

связным, если для любых двух его точек существует содержащий их цикл.

Теперь мы можем сформулировать основной результат.

Теорема. Для любой БД-совершенной идеальной СРС, реализующей структуру дос-

тупа

Г, независимые множества, определяемые условием

log|

| ||VA|| = |A|, задают связный матроид на множестве {0, 1,…, n}. Все циклы этого

матроида, содержащие точку

0, имеют вид 0 ∪ А, где А ∈ Г

min

Доказательство теоремы приведено в соответствующей литературе и выходит за рам-

ки данной книги. Главным в доказательстве теоремы является “проверка” целочислен-

ности функции

h(A). В самом деле, h(A) очевидно обладает остальными свойствами (6)

Секретность и имитостойкость 353

и, следовательно, при условии целочисленности является ранговой функцией и задает

матроид.

Отметим, что из второй части утверждения теоремы следует, что разным идеальным

СРС, реализующим данную структуру доступа

Г, всегда соответствует один и тот же

матроид, поскольку матроид однозначно определяется всеми циклами, проходящими че-

рез фиксированную точку. Тем самым, каждой идеальной реализуемой структуре досту-

па соответствует однозначно определенный матроид.

В связи с теоремой возникает несколько естественных вопросов. Прежде всего, не

порождают ли идеальные СРС все матроиды? Нет, например, матроид

Вамоса не может

быть получен как матроид идеальной СРС. С другой стороны линейные матроиды есть

ни что иное, как рассмотренные идеальные одномерные линейные СРС. В связи с этим

возникает вопрос о существовании структуры доступа

Г, которую невозможно реализо-

вать в виде идеальной одномерной линейной СРС, но можно в виде идеальной много-

мерной линейной СРС. Такие примеры имеются, и, значит, мы можем говорить о мно-

гомерных линейных матроидах как классе матроидов более общем, чем линейные.

Итак, идеальных СРС больше, чем линейных матроидов, но меньше, чем всех

мат-

роидов. Уточнить, насколько больше, представляется довольно сложной задачей. В ча-

стности, существует ли идеально реализуемая структура доступа

Г, которую невозмож-

но реализовать как идеальную линейную многомерную СРС?

Секретность и имитостойкость

Криптографические преобразования обеспечивают решение двух главных проблем

ЗИ: проблемы секретности (лишение противника возможности извлечь информацию

из канала связи) и проблемы имитостойкости (лишение противника возможности

ввести ложную информацию в канал связи или изменить сообщение так, чтобы изме-

нился его смысл).

В случае телефонной связи главной является проблема имитостойкости, поскольку

вызванная сторона не

может часто определить, кто звонит. Подслушивание, требующее

подключения к проводам, технически более сложно и юридически более опасно, чем вы-

зов корреспондента и выдача себя за кого-то другого. В случае радиосвязи ситуация

прямо противоположная. Перехват здесь является пассивным и сопряжен с незначитель-

ной юридической опасностью, тогда как введение информации связано

с риском обна-

ружения незаконного передатчика и юридического преследования.

Проблема секретности

Проблемы секретности и имитостойкости между собой тесно связаны, поэтому мето-

ды решения одной из них часто применимы для решения другой. Из двух названных

проблем проблема секретности обычно рассматривается первой, как более старая и шире

известная. Рассмотрим схему прохождения потока информации в криптографической

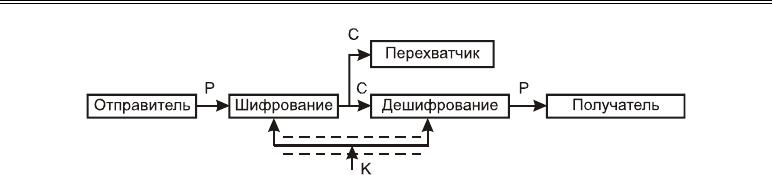
системе, обеспечивающей секретность (рис. 18.3).

354 Глава 18. Криптографическая защита

Рис. 18.3. Поток информации в криптографической системе,

обеспечивающей секретность

Отправитель генерирует открытый текст, или шифрованное сообщение

Р, которое

должно быть передано получателю по незащищенному прослушиваемому каналу. Для

того чтобы перехватчик не смог узнать содержания сообщения

Р, отправитель шифрует

или кодирует его с помощью обратимого преобразования

и получает криптограмму

или шифрованный текст

С = S

(P). Получатель, приняв сообщение С, дешифрирует или декодирует его с помо-

щью обратного преобразования

-1

и получает исходное сообщение

-1

(P)] =P

Преобразование S

выбирается из семейства криптографических преобразований, на-

зываемых криптографической, или общей, системой.

Параметр, выбирающий отдельное используемое преобразование, называется клю-

чом.

Общая система — это набор инструкций, аппаратурных средств и программного

обеспечения ЭВМ, с помощью которого можно зашифровать и расшифровать текст раз-

ными способами, один из которых выбирается с помощью конкретного ключа.

Говоря

более формально, криптографическая система — это однопараметрическое

семейство

)

к∈K

обратимых преобразований S

:Р→С из пространства Р сообщений

открытого текста в пространство

С шифрованных сообщений. Параметр, или ключ К,

называется пространством ключей.

Обычно общая система рассматривается как общедоступная. С одной стороны, от-

крытая для всех часть общей системы является предметом соглашения, а с другой сто-

роны, это отражает очень важное правило техники защиты: защищенность системы не

должна зависеть от секретности чего-либо такого, что нельзя быстро изменить в случае

утечки секретной информации. Обычно общая система является некоторой совокупно-

стью аппаратуры и программ, которую можно изменить только со значительной затра-

той времени и средств, тогда как ключ представляет собой легко изменяемый объект.

Поскольку вся секретность сосредоточена в секретности ключа, то его надо переда-

вать отправителю и получателю по защищенному каналу распространения

ключей, та-

кому, как курьерская служба и т.д.

Проблема имитостойкости

Безусловная и теоретическая стойкость 355

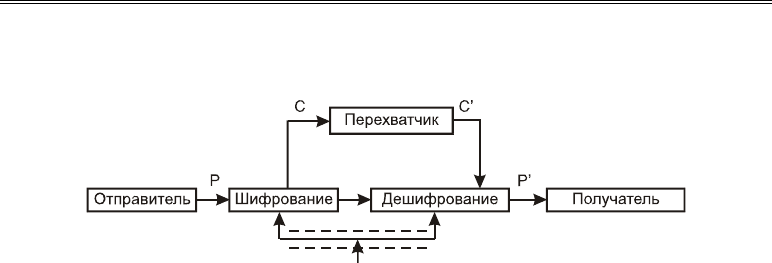
Теперь рассмотрим схему прохождения потока информации в криптографической

системе, обеспечивающей имитостойкость (рис. 18.4).

Рис. 18.4. Поток информации в криптографической системе,

обеспечивающей имитостойкость

При решении проблемы имитостойкости противник может не только видеть все

криптограммы, передаваемые по каналу, но может также изменять их по своему жела-

нию. Законный получатель защищает себя от обмана, дешифрируя все полученные со-

общения и принимая только те сообщения, которые зашифрованы правильным

ключом.

Любая попытка со стороны перехватчика расшифровать криптограмму

С для полу-

чения открытого текста

Р или зашифровать свой текст Р' для получения приемлемой

криптограммы

С' без получения ключа должно быть полностью исключено.

Если криптоанализ невозможен и криптоаналитик не может вывести

Р и С или С'

из

Р' без предварительного получения ключа, то такая криптографическая система являет-

ся криптостойкой.

Безусловная и теоретическая стойкость

Существует два принципиально разных метода обеспечения стойкости криптографи-

ческих систем против криптоаналитического нападения.

В некоторых системах объем доступной криптоаналитику информации фактически

недостаточен для того, чтобы найти преобразования и дешифрирования, причем данная

ситуация не зависит от того, какие вычислительные мощности имеет криптоаналитик.

Система такого рода называется безусловно стойкой.

В том случае, когда

перехваченный материал содержит достаточно информации для

однозначного решения криптоаналитической задачи, нет никакой гарантии, что это ре-

шение будет найдено криптоаналитиком, имеющим определенные вычислительные ре-

сурсы. Следовательно, цель разработчика криптографической системы состоит в том,

чтобы уменьшить затраты на операции шифрования и дешифрирования, но чтобы в тоже

время любая криптоаналитическая операция была

слишком сложной и поэтому эконо-

мически невыгодной. Иными словами, необходимо, чтобы задача криптоанализа, о ко-

торой известно, что она разрешима при конечном объеме вычислений, была бы столь

громоздкой, что для ее решения не хватило бы физических вычислительных ресурсов

всего мира. Задачу такого объема называют вычислительно нереализуемой, а связанную с

ней криптографическую

систему — вычислительно стойкой.

356 Глава 18. Криптографическая защита

В случае безусловно стойких систем их стойкость может быть доказана, но что каса-

ется теории вычислительной сложности, то при нынешнем уровне ее развития она не в

состоянии продемонстрировать вычислительную нереализуемость любой криптографи-

ческой задачи. Поэтому в криптографии возникло и развивается направление, посвя-

щенное разработке формальных процессов проверки стойкости. Такие процессы сводят

ся к криптоаналитическому нападению на предлагаемые для проверки криптографиче-

ские системы при условиях, благоприятных для криптоаналитика.

Единственной безусловно стойкой системой, находящейся в широком пользовании,

является лента однократного использования, в которой открытый текст объединяется

со случайным ключом такой же длины. Обычно открытый текст представляет собой

строку из

n бит, которая объединяются со случайным ключом такой же длины с помо-

щью сложения по модулю 2. Как видно из самого названия, этот ключ никогда больше

не используется.

Даже если бы криптоаналитик попытался осуществить дешифрирование, используя

все

возможных ключей, он просто увидел бы все 2

возможных открытых текстов

одинаковой длины. Поскольку перехват криптограммы не позволяет криптоаналитику

вывести какое-либо сообщение в виде открытого текста, то он не узнает ничего, кроме

длины сообщения. Клод Шеннон анализировал абсолютную стойкость более подробно.

Если криптоаналитик располагает неограниченным временем для вычислений, то он не

связан рамками вычислительной эффективности и может

провести полный криптоана-

лиз, испытывая все возможные ключи и сохраняя в качестве результата все осмыслен-

ные тексты. В случае ленты однократного использования необходимо сохранить все ос-

мысленные тексты, имеющие одинаковую с криптограммой длину, но в других безус-

ловно стойких системах может быть меньшее количество осмысленных решений.

Например, криптограмма XMDA, полученная в результате

простой подстановки годится

для любого четырехбуквенного слова с неповторяющимися буквами.

По мере того как количество перехваченных текстов возрастает, может быть достиг-

нута точка, в которой оказывается возможным получение однозначного решения. Шен-

нон назвал это интервалом однозначности

. В случае ленты однократного использова-

ния этого никогда не случиться, и

= ∞, тогда как в случае простого подстановочного

шифра значение

конечно. Шеннон предложил модель для предсказания интервала

однозначности шифра. Полученные с помощью этой модели результаты согласуются с

практикой. В соответствии с этой моделью “случайного шифра”

H(K)

(18.7)

где H(K) — энтропия ключа (обычно это просто длина ключа, измеренная в битах, или

log

от количества ключей), D — избыточность языка, измеренная в битах на 1 знак.

(Например, в английском языке за буквой Q всегда следует буква U, которая является

избыточной.) Качественно модель можно показать, переписав (18.7) в виде требования

для однозначности решения

H(K) ≤ N

D (18.8)

Безусловная и теоретическая стойкость 357

где H(K) характеризует количество неизвестных в двоичном представлении ключа, а

D в широком смысле определяет количество уравнений, которые необходимо решить

для нахождения ключа. Когда количество уравнений меньше количества неизвестных,

однозначное решение невозможно и система является безусловно стойкой. Когда коли-

чество уравнений больше количества неизвестных, т.е. как в (18.8), однозначное реше-

ние возможно и система не является безусловно стойкой, хотя она все

еще может

быть вычислительно стойкой.

Несмотря на то, что в теории кодирования Шеннона (т.е. в предположении, что крип-

тоаналитик располагает неограниченными ресурсами) обычно рассматривается нападе-

ние при наличии только шифрованного текста, но иногда используются и комбинации

шифрованного и открытого текста, что повышает избыточность.

Уравнение (18.7) показывает ценность снятия данных, производимого перед

шифро-

ванием.

Согласно Фридмэну, почти любая криптограмма из 25 букв и более, полученная

подстановкой, может быть раскрыта. Поскольку криптоаналитик располагает ограни-

ченными вычислительными возможностями, он не может перепробовать все

26! ≈

4.10

ключей и должен полагаться на субоптимальные методы, такие как частотный

анализ. Таким образом, можно сказать, что

= 25 знаков.

В случае ленты однократного использования

H(K) = ∞, откуда, согласно (7), N

= ∞.

После простой подстановки получаем

H(K) = log

(26!) = 88,4 бит, поэтому для вычис-

ления

принято находить D. Каждый знак мог бы переносить максимум log

(26) = 4,7

бит информации, если бы все комбинации были возможны. Но поскольку правила пра-

вописания и грамматики запрещают использование большинства комбинаций, то в сред-

нем каждый знак переносит всего лишь

1,5 бит информации. Оставшиеся 3,2 бит оказы-

ваются избыточными, откуда

D = 3,2 бит/знак. Таким образом, уравнение (18.7) пред-

ставляет величину

= 28 знаков, что хорошо согласуется с практикой.

Например, если перехвачено сообщение длиной в

1000 знаков и известна некоторая

последовательность из

100 знаков открытого текста, то общая избыточность составит не

3200 бит, а (900 знаков) × (3,2 бит/знак) + (100 знаков) × (4,7 бит/знак) = 3350 бит.

Сжатие данных устраняет избыточность, увеличивая тем самым интервал однознач-

ности. Избыточная информация может быть добавлена после дешифрирования. Совер-

шенное сжатие данных устранило бы всю избыточность и привело бы к

= ∞ при лю-

бой длине ключа, но это довольно дорогое мероприятие.

Важным подготовительным этапом для проверки стойкости шифра является проду-

мывание различных предполагаемых возможностей, с помощью которых противник мо-

жет вскрыть шифр. Появление таких возможностей у противника обычно не зависит от

собственно используемого криптографического метода, а является следствием некото-

рой внешней

подсказки, наличие которой существенно влияет на стойкость шифра. По-

этому оценки стойкости шифра всегда содержат те предположения о противнике, в ус-

ловиях которых эти оценки получены.

Прежде всего, обычно считается, что противник знает сам шифр и имеет возможность

его предварительного изучения. Противник также знает некоторые характеристики откры-

358 Глава 18. Криптографическая защита

тых текстов (защищаемой информации), например, общую тематику сообщений, их стиль,

некоторые стандарты, форматы и т.д.

Приведем три примера специфических возможностей противника:

• противник может перехватывать все шифрованные сообщения, но не имеет соответ-

ствующих им открытых текстов;

• противник может перехватывать все шифрованные сообщения и добывать соответст-

вующие им открытые тексты;

• противник имеет доступ к шифру (но не к ключам!) и поэтому может зашифровать

любую информацию.

На протяжении многих веков среди специалистов не утихали споры о стойкости

шифров и о возможности построения абсолютно стойкого шифра.

“Отец кибернетики” Норберт Винер отмечал: “Любой шифр может быть вскрыт,

если только в этом есть настоятельная

необходимость и информация, которую предпо-

лагается получить, стоит затраченных средств, усилий и времени…”

Поэтому у пользователя остается единственный путь — получение практических

оценок стойкости. Этот путь состоит из следующих этапов.

1. Понять и четко сформулировать, от какого противника необходимо защищать ин-

формацию. Следует уяснить, что именно противник знает или может узнать о систе-

ме шифра, какие силы и средства он сможет применить для его вскрытия.

2. Мысленно стать в положение противника и попытаться с его позиций вскрыть шифр,

т.е. разработать различные алгоритмы вскрытия шифра, обеспечивая при этом в мак-

симальной мере моделирование сил, средств и возможностей противника.

3. Наилучший из разработанных алгоритмов использовать для практической оценки

стойкости шифра.

Следует упомянуть о двух простейших методах вскрытия шифра: случайного угады-

вания ключа (он срабатывает с малой вероятностью, но является самую низкую вычис-

лительную сложность) и перебора всех подряд ключей вплоть до нахождения истинного

(он срабатывает всегда, но имеет самую высокую

вычислительную сложность).

Анализ основных криптографических методов ЗИ

Иногда криптографические методы ЗИ разделяют на три группы: методы подста-

новки, методы перестановки и аддитивные методы. Методы перестановки и подста-

новки характеризуются хорошими ключами, а их надежность связана со сложным алго-

ритмом преобразования. При аддитивных методах пользуются простыми алгоритмами

преобразования, обеспечивая надежность с помощью ключей большого объема.

Иногда говорят о блочных

методах, имея в виду первые две группы, в которых ал-

горитм работает сразу над большим блоком информации, и о потоковых методах, где

шифрование происходит знак за знаком. Однако при использовании аддитивных мето-

дов преобразование может осуществляться сразу над целым машинным словом и метод

приобретает признаки блочного.

Анализ основных криптографических методов ЗИ 359

Шифрование методом подстановки (замены)

В этом, наиболее простом, методе символы шифруемого текста заменяются другими

символами, взятыми из одного (моноалфавитная подстановка) или нескольких (полиал-

фавитная подстановка) алфавитов. Самой простой разновидностей является прямая за-

мена, когда буквы шифруемого текста заменяются другими буквами того же самого или

некоторого другого алфавита.

Если объем зашифрованного текста большой, то частоты появления

букв в зашифро-

ванном тексте будут ближе к частотам появления букв в алфавите (того языка, на кото-

ром написан текст) и расшифровка будет очень простой.

Поэтому простую замену в настоящее время используют редко и в тех случаях, когда

шифруемый текст короток.

Для повышения стойкости шифра используют так называемые полиалфавитные под-

становки, в которых для замены символов исходного текста используются символы не-

скольких алфавитов. Существует несколько разновидностей полиалфавитной подста-

новки, наиболее известными из которых являются одно- (обыкновенная и монофониче-

ская) и многоконтурная.

При полиалфавитной одноконтурной обыкновенной подстановке для замены симво-

лов исходного текста используется несколько алфавитов, причем смена алфавитов осу-

ществляется последовательно

и циклически, т.е. первый символ заменяется соответст-

вующим символом первого алфавита, второй — символом второго алфавита и т.д. до тех

пор, пока не будут использованы все выбранные алфавиты. После этого использование

алфавитов повторяется.

В качестве примера рассмотрим шифрование с помощью таблицы Виженера. Таблица

Виженера представляет собой матрицу с

элементами, где n — количество символов

используемого алфавита. Каждая строка матрицы получена циклическим сдвигом алфа-

вита на символ. Для шифрования выбирается буквенный ключ, в соответствии с кото-

рым формируется рабочая матрица шифрования. Осуществляется это следующим обра-

зом. Из полной таблицы выбирается первая строка и те строки, первые буквы которых

соответствуют буквам ключа. Первой размещается

первая строка, а под нею — строки,

соответствующие буквам ключа в порядке следования этих букв в ключе.

Сам процесс шифрования осуществляется следующим образом:

• под каждой буквой шифруемого текста записывают буквы ключа (ключ при этом по-

вторяется необходимое количество раз);

• каждая буква шифруемого текста заменяется по подматрице буквами, находящимися

на пересечении линий, соединяющих буквы шифруемого текста в первой строке

подматрицы и находящихся под ними букв ключа;

• полученный текст может разбиваться на группы по несколько знаков.

Исследования показали, что при использовании такого метода статистические харак-

теристики исходного текста практически не проявляются в зашифрованном тексте. Не-

трудно заметить, что замена по таблице Виженера эквивалентна простой замене с цик-

лическим изменением алфавита, т.е. здесь мы имеем полиалфавитную подстановку, при

360 Глава 18. Криптографическая защита

чем число используемых алфавитов определяется числом букв в ключе. Поэтому стой-

кость такой замены определяется произведением прямой замены на количество исполь-

зуемых алфавитов, т.е. на количество букв в ключе.

Одним из недостатков шифрования по таблице Виженера является то, что при не-

большой длине ключа надежность шифрования остается невысокой, а формирование

длинных ключей сопряжено с определенными трудностями.

Нецелесообразно выбирать ключи с повторяющимися буквами, так как при этом

стойкость шифра не возрастает. В то же время ключ должен легко запоминаться, чтобы

его можно было не записывать. Последовательность же букв, не имеющих смысла, за-

помнить трудно.

С целью повышения стойкости шифрования можно использовать

усовершенствован-

ные варианты таблицы Виженера. Отметим некоторые из них:

• во всех (кроме первой) строках таблицы буквы располагаются в произвольном по-

рядке;

• в качестве ключа используются случайные последовательности чисел.

Из таблицы Виженера выбираются десять произвольных строк, которые кодируются

натуральными числами от 0 до 10. Эти строки используются в соответствии с чередова-

нием цифр в выбранном ключе.

Частным случаем рассмотренной полиалфавитной подстановки является так назы-

ваемая монофоническая подстановка. Особенность этого метода состоит в том, что ко

личество и состав алфавитов выбираются таким образом, чтобы частоты появления всех

символов в зашифрованном тексте были одинаковыми. При таком положении затрудня-

ется криптоанализ зашифрованного текста с помощью его статической обработки. Вы-

равнивание частот появления символов достигается за счет того, что для часто встре-

чающихся символов исходного текста предусматривается использование большего

чис-

ла заменяющих элементов, чем для редко встречающихся.

Полиалфавитная многоконтурная подстановка заключается в том, что для шифро-

вания используется несколько наборов (контуров) алфавитов, используемых цикличе-

ски, причем каждый контур в общем случае имеет свой индивидуальный период приме-

нения. Этот период исчисляется, как правило, количеством знаков, после зашифровки

которых меняется контур алфавитов

. Частным случаем многоконтурной полиалфавит-

ной подстановки является замена по таблице Вижинера, если для шифрования использу-

ется несколько ключей, каждый из которых имеет свой период применения.

Общая модель шифрования подстановкой может быть представлена в следующем

виде:

= t

+ ω mod (K – 1)

где t

— символ зашифрованного текста; t

— символ исходного текста; ω — целое чис-

ло в диапазоне от

0 до (К–1); К — количество символов используемого алфавита.

Если

ω фиксировано, то формула описывает моноалфавитную подстановку, если ω

выбирается из последовательности

, ω

, …, ω

, то получается полиалфавитная под-

становка с периодом